无信号灯交叉路口智能车辆调度算法研究

谢彭辉,孙 宁,庞 堯,赵文骞,钱俊杰

(1.南京林业大学汽车与交通工程学院,江苏 南京 210037;2.南京林业大学信息科学技术学院,江苏 南京 210037)

0 引言

随着无人驾驶技术的快速发展,智能车辆在无信号灯交叉路口的通行调度成为研究热点[1-2]。智能车辆在交叉路口的通行效率与其通过速度、调度策略相关。因为交叉路口一般会限定最高通过速度,所以调度策略的优劣会直接影响车辆在交叉路口的通行效率和行驶安全。受传感器范围限制以及周围复杂环境对电磁信号的阻挡,智能车辆无法感知交叉路口的全局信息,导致交叉路口的全局调度难以实现。这不仅降低了车辆的通行效率,还增加了交通事故的发生概率[3]。相关的调度方案主要分为集中式和分布式这2类。

集中式调度以全局最优为调度目标,由智能路基单元收集全局信息并进行算法处理,从而将调度策略发送至每个进入交叉路口的车辆[4]。

集中式车辆调度模式简单,但对路基单元的算力要求较高,且系统可靠性差。分布式调度去除中心化,由智能车辆利用车载传感器感知局部信息进行调度规划,使每辆车在一定情况下承担了一定的任务。这简化了调度时需要处理的信息量[5],具有良好的应用前景。

吴伟等[6]提出了基于网格化基础的交叉路口车辆调度优化模型,使用分支定界法获得车辆最佳路径。此方法中的模型简明易懂,但属于静态算法,不适用于存在多车辆通过的路口调度场景。姜辰凯等[7]提出了改进的Dijkstra算法,可实现多个自动导引运输车(automated guided vehicle,AGV)的动态路径规划。该算法能在最优路径下避免冲突,具有较好的鲁棒性。

本文提出了基于动态网格权值的调度算法。网格权值法是1种分布式车辆调度方案。其基本原理是:将交叉路口的冲突区看作1个网格图;每个网格的权值不同;车辆根据网格权值选择下一步进入的网格,以得出最优调度策略。基于动态网格权值的调度算法能够有效解决冲突碰撞问题,为提高车辆在交叉路口的通过效率提供了可行思路。

1 系统模型

智能车辆能感知一定范围内的信息,以获取地理位置、瞬时车速、行驶方向角等。本文假定有1个无信号灯控制的网格化后的双向六车道交叉路口[8],并定义网格区为车辆冲突区域。根据相关交通法律规定,车辆在进入冲突区后不得变换车道[9]。每个网格仅能容纳1辆车。车辆在冲突区的前进方向只可以直行或以1°～90°转弯,且车辆每次都行驶至每个网格的中心位置。每个网格都为正方形。权值设置如下。

①方向权值ε。本文设:车辆当前所处网格中心与终点网格中心的连线为标准线;车辆行驶方向(即车头朝向)与基准线夹角为θ;ε=cosθ。θ越大,则ε越小。方向权值可以使车辆行驶路径b向初始静态最优路径a逼近,并确保车辆不偏航。

②预警权值δ。车辆在直行或转向至下个行进网格时:若下个网格已被其他车辆占用,则规定下个网格的δ为0.4(下个回合车辆已驶出该网格);若下个网格也同时被其他车辆选中为行进方格,则规定下个网格的δ为0.1;若下个网格未被其他车辆选中且未被占用,则规定下个网格的δ为0.8。

③转向权值β。本文规定车辆在左侧左转、右侧右转、直行时的β分别为0.3、0.6、0.9。

本文根据得到的综合权值ω=ε×δ×β,先对行驶进冲突区车辆的综合权值进行实时更新,以得到可变的综合权值;再根据综合权值实时更新车辆的路径,使车辆能尽快到达终点网格。

2 算法设计

2.1 底层算法逻辑设计

底层算法流程如图1所示。

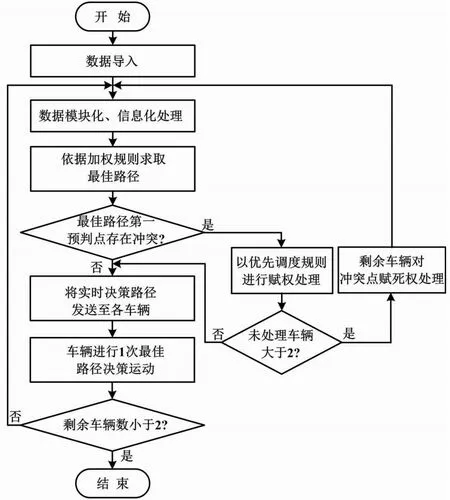
图1 底层算法流程图

2.2 算法实现过程

算法实现分为2个步骤,分别为寻径和冲突调度。

2.2.1 寻径

本文将车辆实体和运动背景以单元格实例化,并规定车辆每次只移动1个单元格。

本文跳出混合迭代贪婪算法(greedy algorithm,GA)[10-11]只在已有方案中寻找最优,而不能提供新方案的局限,以避免基于经验选择的贪婪思想的弊端。

本文假设路径集P为网格中从源节点到目标节点所有路径的集合。路径集P分为几类路径子集:P1为只有1条边的路径;P2为只有2条边的路径;依次类推。因为每条边的权值不同,所以P2中路径的长度不一定比P1大。

贪婪选择过程如下。现假设车辆A从网格13出发,终点为网格34。根据权值设置原则与缩短搜索半径规则,以车辆A为主体进行首次贪婪性质选择,得到最佳路径序列为{13,20,27,34}。当车辆A运动至网格20时,车辆B直行也选中网格27为最佳路径。这时,对车辆A、B进行冲突调度处理。假设处理结果为车辆B拥有27网格的优先行驶权,此时车辆A要到达终点方格,则需要作出对最佳路径的更新。对27网格设为死权(无法选取),由此车辆开始进行第二次贪婪性质选择,即网格20。此时拥有2条有向路线可作为首项元素进行加权选择{21,26}。对于21→34、26→34这2条单源最短路径的选取,则需要遍历邻接顶点,并比较得到1条或多条最短路径。以上过程体现为:车辆在不断地进行“贪婪选择”与“位置移动”决策,直至车辆到达目标位置。其整体上呈现为GA在动态过程的递推增强。

调度模型如图2所示。

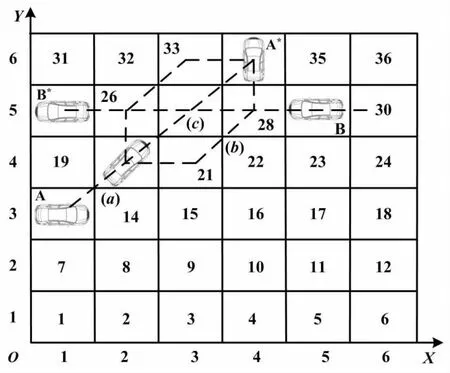
图2 调度模型

图2中:a为未经调度处理的车辆A行驶路线;b为经过调度处理的车辆A行驶路线;c点为车辆A、B未经调度处理的冲突点。

引申至当n辆车在网格中行驶时,上述情况在每辆车运动时都会发生,则需要不断地对每辆车的最佳路径作出实时动态处理,直至每辆车都拥有各自的寻优路径为止。

本文采用一维数组α[v]={v0,v1,…,vn}来保存顶点到源顶点的路径长度,并初始化路径长度为无穷大。本文用一维数组α[s]={s0,s1,…,sn}来保存顶点所在最短路径的前驱顶点,以便输出路径。本文使用1个数据结构来保证每次从未确定最短路径的顶点中提取出路径最短的顶点。

同时,为了避免单邻域操作的重复贪婪搜索过程容易陷入相应邻域结构的局部最优解,本文根据混合迭代GA[10]的思想,进一步对有潜力区域作更深入的检索。检索伪代码如下。

Foreachv!=s: α[v]←∞,pred[v]←null;α[s]←0;

Creat an empty priority queue PQ;

Foreach v∈V:Insert(PQ,v,α[v]);

While(is-not-empty(PQ))

u←Del-Min(PQ); //提取局部优解

Foreach edge e =(u,v)leaving u: //局部优解重检索

If(α[v]>α[u]+l)

Decrease-Key(PQ,v,α[u]+l)

α[v]←α[u]+l;

pred[v]←u;

本文通过对车辆运动的周围临界区作循环遍历处理,根据所提出的权值规则初步求出优解,进一步根据优解的下一步择径作出有效判别,以实现混合迭代求径并提取最优解。

基于以上分析,本文对需要对最佳路径作出重新选择的车辆进行循环,直到即将行驶的最佳路径方格不存在冲突点为止。

2.2.2 冲突调度

本文构造1个车辆类,并在该类中设置属性变量元素。属性变量元素包括车辆的名称编号、优先级、最佳路径序列、最佳路径序列的长度。冲突调度时规则的设置是依照车辆类内属性变量依次作出优先选择权判断。

(1)优先运行原则。

①优先级。优先级高者通行。

②最佳路径序列剩余量。剩余量少者通行。

③车辆名称编号。美国信息交换标准代码(American standard code for information intercharge,ASCII)小者通行。

本文对车辆进行实例化对象构造,创建冲突调度所需要使用到的各因子。因子包括优先级、最佳路径序列、序列组长和名称编号。本文封装录入方法成员函数和类外调度方法函数,并导入所有车辆属性信息。

车辆冲突调度样例如表1所示。

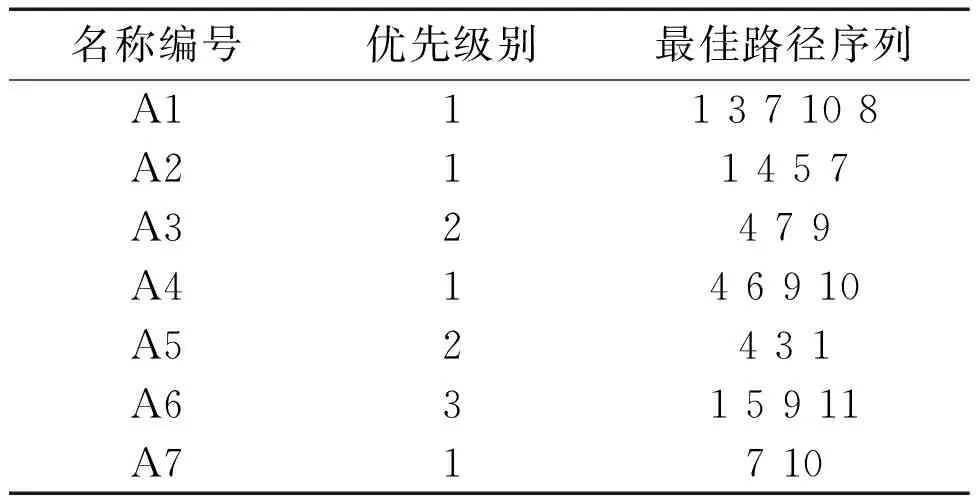
表1 车辆冲突调度样例表

属性比较顺序为优先级>序列剩余量>ASCII。

(2)通行优先级比较流程。

①创建1个类数组array。在这样1个数组中存储着各车辆类与其属性信息。

②以最佳路径序列的第一项元素作为需求值,将需求值自小到大进行排序,使得存在冲突点的车辆在数组内以区间形式存储。通过这样的处理,可以得到1个以冲突点划分区间的排序数组。

③对有冲突点的车辆元素,作出优先级比较处理,以此进一步筛选出拥有优先通行权的车辆。

④优先序列排序。

车辆交换排序的C++伪代码如下。

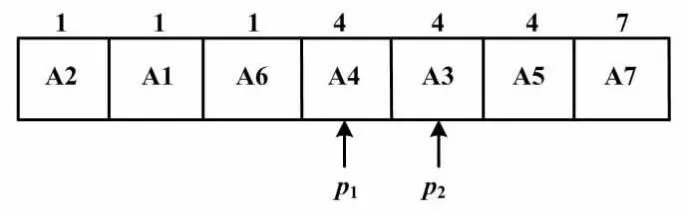
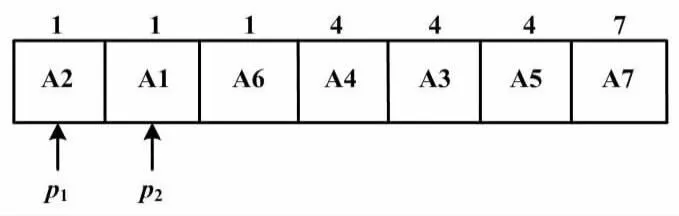
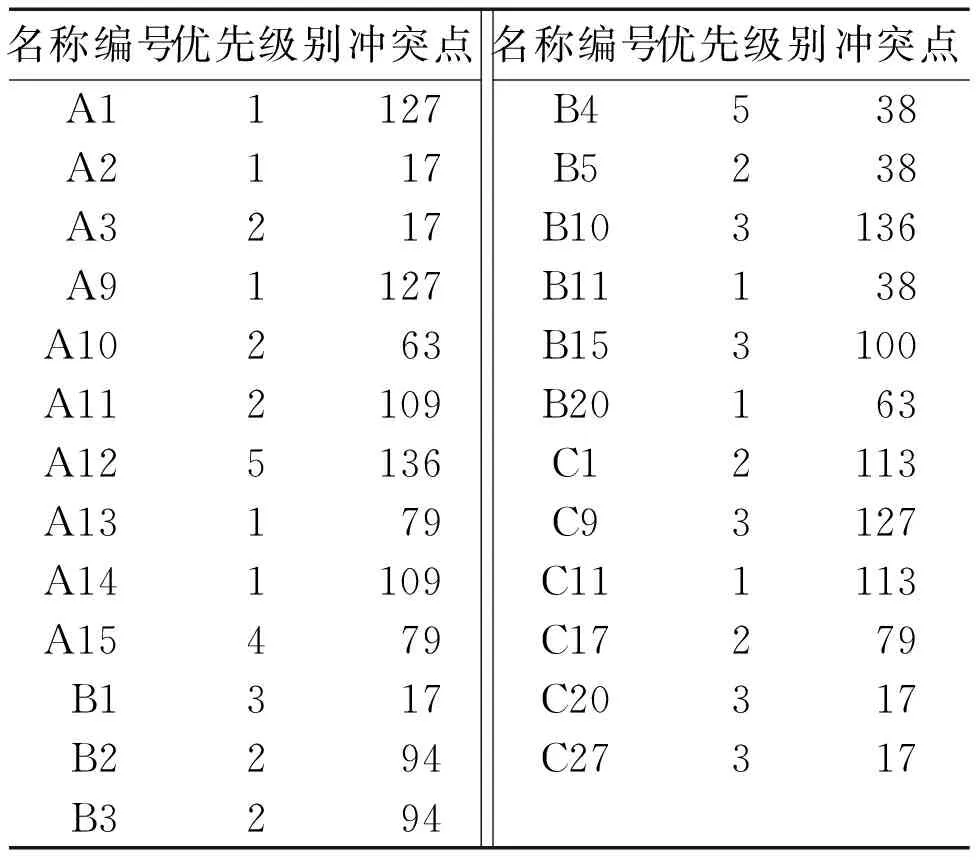
for(i=0;i

{

for(j=0;j

{

if(j+1

swap(j+1,j)

}

}

⑤重复上述操作,进行ASCII的比较,即可得到数据处理结果。该结果是根据上述条件进行调度排序之后的结构数组。处理后的数组中,准确的表示应为array[0]中存储着车辆A2的名称编号、优先级、最佳序列及其长度。而在每次贪婪性质选择时,并不需要关心整体的最佳序列,只需要了解最佳序列中存在的冲突点,并作出区块分类。所以,以冲突点替换序列能更直观地表现出经过上述排序之后的结果。

车辆调度排序处理结果如表2所示。

表2 车辆调度排序处理结果

经过以上数组处理之后,易得在每个冲突点的区块之中,区块的第一个位置存储的就是该冲突点的最优先行驶车辆。例如:A2、A1、A6在冲突点1区块之中;A4、A3、A5在冲突点4区块之中。那么,A2与A4是在其对应的冲突点中最优先行驶的车辆。

底层指针初始采取双指针处理。本文设置指针p1指向数组第一个元素、指针p2指向数组第二个元素。

底层指针初始化如图3所示。

图3 底层指针初始化示意图

p2不断往后对数组进行扫描,并校验冲突点是否相等,同时需控制p2不要超过数组。p1与p2所指向的车辆的冲突点不一致时,返回p1所指向的车辆。该车辆就是该冲突区块优先车辆。例如:p1指向类数组的第一个位置(A2);p2指向类数组的第二个位置(A1);p2不断向后移动,直到p2指向数组的第四个位置(A4)时,p1的冲突点不为p2的冲突点,则返回p1所指向的车辆。由此完成1个冲突区块的优先车辆提取。

在提取优先车辆后,p1指向p2所指向的车辆,而p2继续往后进行数据扫描和校验。

底层数据结构指针移动如图4所示。

图4 底层数据结构指针移动示意图

指针移动的C++伪代码如下。

if(p1.冲突点!=p2.冲突点)

p1=p2;

p2=car[i+1];

return p1车辆;

}

实现过程使用单层循环、双指针、时间复杂度T(n)、空间复杂度O(n)。以此不断重复上述操作,直到p2指针超出数组范围。此时,指针返回p1所指向的车辆。至此,算法进程结束。

3 数据试验

在算法运行过程中,本文取一次调度环节进行试验。整体运作过程为:①数据导入;②加权求取最佳路径;③冲突判断并调度;④校验无误后数据结果传输至硬件层并开始运作。

此过程需循环执行步骤②和步骤③,直至得到无冲突的全局最优解。试验在程序中导入15×15的网格,并输入25组数据进行校验。

参考图2所示的6×6网格规律,每个网格由数字标号代表,则计算机内表示方法为:y=(数字标号/x轴长)+1;x=数字标号%x轴长。如网格127冲突点,即为(7,9)位置。

试验根据2.2节作数据处理。数据分析结果如表3所示。由表3可知,冲突点{17,38,63,79,94,100,109,113,127,136}存在。本文使用C++(GDB/LLDB)对数据进行处理,并导出数据结果。得到的调度优先权结果为:在网格17处,B1拥有优先行驶权;在网格38处,B11拥有优先行驶权;在网格63处,B20拥有优先行驶权;在网格79处,C17拥有优先行驶权;在网格94处,B2拥有优先行驶权;在网格100处,B15拥有优先行驶权;在网格109处,A14拥有优先行驶权;在网格113处,C11拥有优先行驶权;在网格127处,A9拥有优先行驶权;在网格136处,B10拥有优先行驶权。本文可进一步得到调度后各车辆的调度路径结果。

表3 数据分析结果

例如A10、B20存在着63(x=3,y=5)的冲突点。在作出调度判断之后,B20具有此位置的优先选择权。此时,A10对A20车辆做出避让措施,并重新选择了62(x=2,y=5)作为新的路径网格。进行了上述的预警调度之后,即可以有效地规避最佳路径的冲突选择。通过如上数据导入试验,可以得到智能车辆防撞的整体调度在软件算法层的理论结构可行性。

4 结论

本文在刘庭玮等[11]提出的基于经验选择的贪婪思想基础上,对GA进行了动态增强。这着重体现在GA的贪婪选择并不是在一次基于经验选择之后结束,而是伴随着整个流程的运作过程不断地进行经验选择,直到流程结束。本文对GA进行了试验性尝试并补充了对冲突车辆调度的方案,使动态寻径与动态调度相结合,得到1套完整的车流运动控制方案。该方案为车辆高速移动场景下无信号灯交叉路口智能车辆的运行提供了良好的防撞调度措施。后续研究将优化赋值原则,以探讨复杂情况下的权值分配方法。