光伏发电系统最大功率跟踪方法研究

牟 令,陈 俊,陈 侃,杨德超,刘必武,滕 易

(1.湖北能源集团新能源发展有限公司,湖北 武汉 430000;2.三峡大学信息技术中心,湖北 宜昌 443002)

0 引言

在各种类型的可再生能源中,太阳能[1]是应用较广泛的能源之一。因此,基于安装简单、安全性高、无污染、维护少和无噪声等优点,光伏[2-3](photovoltaic,PV)发电在输电网中发挥着越来越重要的作用。

PV系统运行的关键任务之一是在不同天气条件下获取最大可用太阳能。该任务可转化为PV最大功率跟踪问题[4]。目前,许多学者对PV系统最大功率跟踪问题进行了研究,并取得了丰硕成果。文献[5]提出了1种结合自适应布谷鸟搜索算法和扰动观察方法的复合跟踪算法。该算法将布谷鸟搜索算法中的切换概率和Lévy飞行步长系数自适应调整,以改善模型搜索能力。文献[6]提出了1种改进细菌觅食算法求解最大功率跟踪算法,从而避免输出功率来回振荡。上述算法均为典型的启发式算法。然而,启发式算法容易在不同的运行中收敛到不同的最优解。近年来,强化学习[7](reinforcement learning,RL)以其卓越的在线学习能力而吸引了学者们广泛的关注。与启发式算法相比,RL具有更高的收敛稳定性和更强的学习能力。文献[8]提出了1种基于深度RL算法的PV-抽蓄互补系统智能调度模型,解决了PV发电功率预测精度不高的问题。文献[9]提出了1种基于连续型深度确定性策略梯度算法的微电网能量调度方法。该方法基于马尔可夫开发决策过程建立模型状态、动作空间以及奖励因子,并通过长短期记忆模型提取时序变量数据,从而在调度空间中提升深度RL模型的收敛性。然而,最大功率的高随机性以及天气条件的多变性使解空间较大。传统的RL搜索能力较低,导致模型易陷入局部最优。

为改善上述问题,本文提出了1种改进的模因RL模型。该模型可解决部分遮光条件下PV系统最大功率跟踪问题。该模型将传统RL模型中单智能体改进为多智能体,并基于模因寻找局部最优和全局最优。本文以某市气象数据为例,验证了所提模型的有效性。

1 PV系统建模

1.1 PV电池建模

PV电池通常为P-N型半导体二极管,可将太阳能转换为电能。

PV电池等效电路如图1所示。

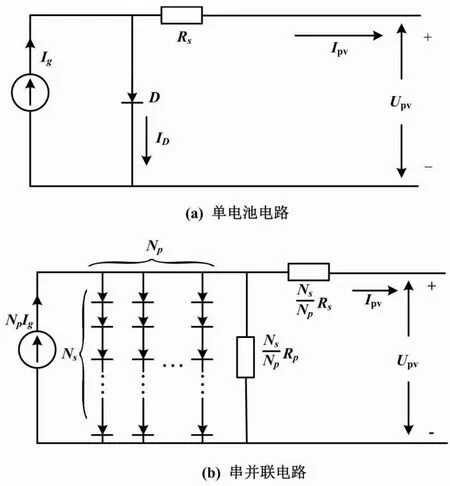
图1 PV电池等效电路

PV电池等效电路包括1个光电流源、1个并联二极管和1个串联电阻。通常,多个PV电池组合在一起形成PV模块。这些模块以串联和并联方式组合,从而提供所需的输出功率。本文令串联和并联的PV电池的数量分别为Ns和NP,则输出电流和电压之间的关系为:

(1)

式中:Ipv为PV输出电流;Np为并联的PV面板数量;Ig为电池光电流;Is为电池反向饱和电流;q为电子电荷,通常取1.602 177 33×10-19Cb;B为理想因子,通常取1～5之间的整数;k为波尔兹曼常数,通常取1.380 658×10-23J/K;Tc为电池的绝对工作温度;Upv为PV输出电压;Ns为串联的PV面板数量;Rs为电池串联电阻。

产生的Ig由太阳辐射确定。

(2)

式中:ki为电池短路电流温度系数;Tref为电池参考温度;Ts为太阳总辐射。

PV的Is根据以下关系随温度而变化:

(3)

式中:IRS为电网电流的D-Q分量;Eg为电池中使用的半导体能隙。

式(1)～式(3)表明,由PV阵列产生的电流同时依赖于太阳辐射和温度。

1.2 部分遮光条件

当串联电路中的1个模块由于遮挡(如灰尘、树木、鸟类等)而在太阳下暴露出较少部分,其电压将下降,工作模型表现为负载单元而不是发电单元。这种情况下将产生1个热点温度。为保护PV模块免受潜在损坏,通常将1个旁路二极管与每个PV模块并联。此外,每个串联电路的末端还连接了1个阻断二极管,以防止并串联之间的电压失配导致的反向电流。

尽管二极管能够避免上述问题,但其不可避免地会改变PV特性并产生双峰曲线。因此,PV系统应始终跟踪全局最大功率,以便从PV阵列中提取最大可用的太阳能资源。否则,其运行时将会损失大量功率,从而造成能源浪费。

2 最大功率跟踪模型

本节建立了基于模因RL的有遮挡PV系统最大功率跟踪模型。本文首先对PV系统最大功率跟踪模型进行建模;其次介绍了模因RL建立过程;最后对模型详细过程进行介绍。

2.1 模型建立

根据前述分析,当串联电路中的1个模块由于遮蔽而暴露出较少的光照时,其电压将下降。此时,旁路二极管与每个PV模块并联,以保护遮蔽模块免受潜在损坏。此外,每个串联电路的末端还连接了1个阻塞二极管,以提供对并联串之间电压失配引起的反向电流的保护。然而,二极管将改变光伏特性并产生双峰线。为改善上述问题,有必要对PV最大功率点进行跟踪。

部分遮挡情况下,PV系统最大功率跟踪模型结构如图2所示。

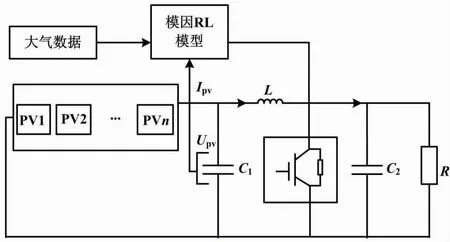
图2 PV系统最大功率跟踪模型结构

PV系统最大功率点可以通过调节有遮挡下的PV系统以输出电压Upv实现。因此,Upv可视为优化变量,且存在下限和上限。通过将输出有功功率的最大化作为目标函数,有遮挡下的PV系统最大功率点优化模型为:

(4)

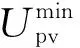
2.2 基于模因的RL模型

模因算法[10]是1种通过连续的交互和进化解决特定优化问题的计算智能模型。模因算法旨在通过基于种群的全局搜索和基于多模因的局部搜索的有效合作,提高搜索效率和种群多样性。为提高搜索效率,本文将模因算法和RL模型相结合,提出了1种基于模因的RL模型,从而提高模型局部和整体搜索能力。

2.2.1 模型建立

Q学习[11]是RL中的主流局部搜索算法之一。Q学习一般只使用单个智能体与环境交互。在当前状态下作出决定后,该智能体可以根据反馈奖励更新知识。因此,Q学习容易导致低学习效率。为了处理这个问题,本文引入模因概念,使用1组协作的智能体来更新Q学习的知识矩阵,同时使用实编码关联存储器将原始的大规模知识矩阵分解为多个小规模知识矩阵。参考Q学习的学习规则,每个模因的知识矩阵可以更新为:

(5)

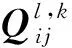
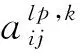
(6)

式中:q0为从0到1均匀分布产生的随机值;ε为选择贪婪行为的概率权重;arand为从动作集合中选择的随机动作。

为了避免模型陷入局部极值状态,种群将根据所有智能体的优缺点重新组合成不同的模因。本文使用基于洗牌蛙跳算法(shuffled frog leaping algorithm,SFLA)的种群划分规则进行全局信息交换。因此,可以根据最大优化的适应度值的降序来实现种群划分过程。第i个模因更新可以描述为:

Yi=[xp,fp∣xp=xi+n(y-1),fp=fi+n(y-1)],p=1,2,…,Ps,i=1,2,…,na

(7)

式中:Yi为第i个模因状态;xp和fp分别为第p个智能体的解和适应度值。

2.2.2 模型求解

根据式(4)中输出电压的最小值和最大值,可以基于所选动作转换智能体的解。

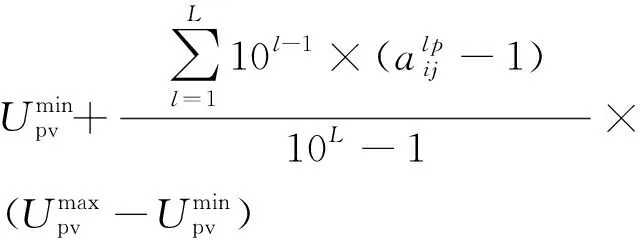
(8)

式中:xip为第i个模因中第p个智能体获得的解。

一般而言,具有较大适应度值的动作将获得更高的反馈回报。为了加快学习速度,本文在模因RL模型中利用蚁群的协作机制设计反馈奖励。

(9)

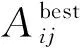
模型选择最佳状态-动作对集合中的值时存在奖励,而其他情况奖励为0。这种机制确保了模型优先从最佳状态-动作对集合选择高奖励策略。

当天气条件变化时,PV系统的输出特性也会随之改变。因此,不同控制策略的反馈奖励将受到天气的直接影响。模因RL模型将根据更新的反馈奖励快速搜索高质量的最优值,以近似追踪PV系统的全局最大功率跟踪点。因此,所提模型可以有效地处理一天中不同时间以及不同季节的天气变化。

模因RL执行流程如图3所示。

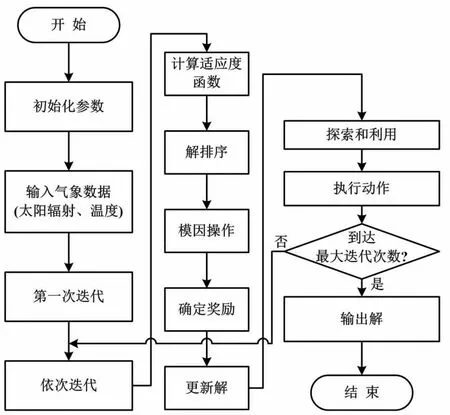
图3 模因RL执行流程图

3 案例与分析

为了评估所提模型性能,本节对不同场景下的PV系统运行变化进行了测试。同时,本文将所提模型与遗传算法(genetic algorithm,GA)、粒子群优化(particle swarm optimization,PSO)算法、人工蜂群(artificial bee colony,ABC)算法、灰狼优化(grey wolf optimization,GWO)算法、教学优化(teaching-learning-based optimization,TLBO)算法的性能进行了比较。

模因RL参数设置如下:模因数为30;每个模因中的种群数量为100;学习率为10-2;学习率衰减系数为10-4;最大迭代次数为104。试验软件环境为Matlab 2019A。同时,算法运行硬件环境为酷睿i7中央处理器(central processing unit,CPU)、内存32 GB ARM的联想服务器。操作系统为Windows 1 064位。

3.1 数据

案例分析数据为某市2022年4个季节中4个典型日的现场大气数据。其中:太阳辐射范围为0～1 000 W/m2;数据收集间隔为10 min。

数据集中部分大气数据如图4所示。

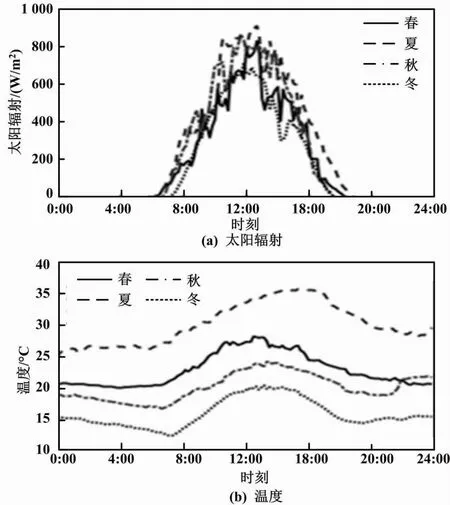
图4 数据集中部分大气数据

由图4可知,4个季节太阳辐射数据和温度数据具有时间周期变化趋势。在图4(a)中,通常在12∶00太阳辐射值最大;在图4(b)中,在12∶00～16∶00 温度最高、4∶00～8∶00温度最低。数据统计结果符合实际情况,反映了数据的周期性趋势。

3.2 统计分析

为了定量评估PV系统的功率波动,试验引入了PV系统功率输出的平均变异性和最大变异性这2个指标:

(10)

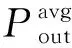
(11)

式中:Δvmax为PV系统功率输出的最大变异性。

4个季节的模型运行统计结果如表1所示。

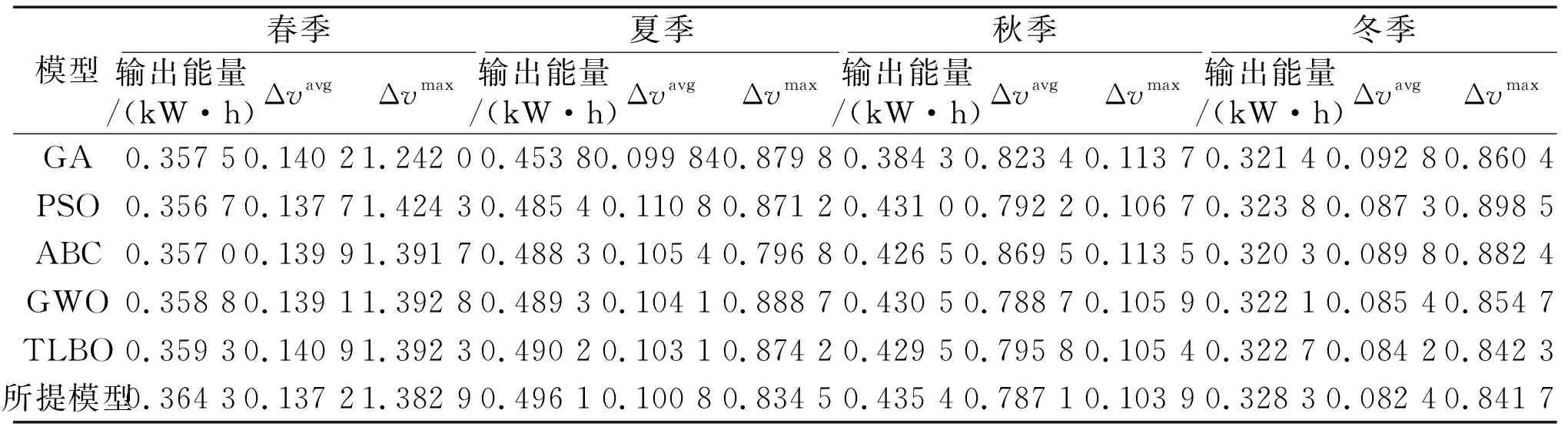
表1 模型运行统计结果

由表1可知,在所有算法中,所提模型拥有最高的输出能量和最小的功率变化。特别是在太阳辐射阶跃变化下,所提模型的平均变异性最低。这表明模型具有较强的鲁棒性。此外,所提模型在冬季产生的输出能量最高,表明模型能够有效跟踪PV最大功率,从而验证了模型的稳定性。

4 结论

为有效跟踪光伏发电系统最大功率点,本文对PV发电系统进行了研究与分析,建立了1种基于计算智能的PV发电系统最大功率跟踪模型。该模型基于部分遮挡条件下的PV系统建模,可解决PV系统最大功率跟踪问题。为提高搜索效率,本文将模因算法和RL模型结合,提出了1种基于模因的RL模型,从而提高模型局部和整体搜索能力。试验时,本文对春季、夏季、秋季、冬季具有周期性的数据进行测试。与主流算法相比,所提模型拥有最高的输出能量和最小的功率变化。试验结果表明,所提模型能够有效跟踪PV最大功率,验证了模型的稳定性和鲁棒性。所提模型为PV能源的高质量能效利用提供了借鉴。

未来可对系统数据安全管理领域进行研究,如引入区块链、云计算等技术以提高混合配电网数据交互可靠性及效率,从而进一步改进智能化电力故障诊断及定位方案。