有源电力滤波器补偿的PI解耦控制技术研究

孙文革

(新疆职业大学机械电子工程学院,新疆 乌鲁木齐 830013)

0 引言

电网中设备的不断增加,导致内部谐波频繁出现[1],进而对整体电力系统产生影响。电网中的谐波会降低电能生产、线路传输和用户侧利用效率,引起电器装置的振动和噪声[2],导致设备使用时间减少甚至报废[3]。谐波会在电网中产生并联或串联共振,导致电网中的谐波增大,使电气电容和其他器件出现烧损的情况。同时,谐波会造成继电保护的误动[4],导致电力计量误差。高频率的谐波会对通信、电子仪表等造成影响。电网中有各种各样的电力系统无功补偿设备,可用于提高电力网的效率、减少设备和传输损耗、降低整体网损。但是,电网无功补偿装置容易与电网系统中的阻抗发生谐振,进而导致谐波放大和电压波动等诸多问题。如何对电力系统进行有效的治理和解耦控制,是当前亟待研究的重要课题。

为此,樊启高等[5]提出了一种两相交叉三电平变换器功率均衡解耦控制方法。该方法分析变换器电路的工作机理,利用两相交叉三电平获得等效两电平。该方法通过采样功率均衡解耦控制方法,令变换器电压和电流完成全部解耦;将四通道取样电路缩减为两通道,以实现简单控制;通过构建等效结构下的小信号模型,设计控制器参数,从而完成解耦控制。王荣闯等[6]提出了三端变换器的解耦控制方法。该方法利用开关元件多路复用,增加功率密度;通过脉宽调制(pulse width modulation,PWM)和双相移控制,在三个端口之间灵活地调节输出功率;采用电感-电容-电感的共振特征,使系统在基频上的功率系数达到1。对三端变换器工作机理、控制模式和谐波特征作深入分析,可以有效减小多通道之间的耦合、提升系统动态响应性能。但上述方法存在控制效果不佳的问题,仍会导致设备以及电力系统不稳定。

因此,本文设计了基于有源电力滤波器补偿的比例积分(proportional integral,PI)解耦控制技术。该技术通过构建滤波器模型,明确内部结构装置、分析滤波器各部分可逆性,以获得旋转坐标线性化;利用瞬态无功与旋转坐标变换方法,输入各次谐波的幅度,以实现解耦控制。试验结果表明,所提技术能够使有源电力滤波器中的谐波电流成分得到充分的解耦。

1 有源电力滤波器设计

有源电力滤波器主回路为二极管钳位式变流器[7]。本文通过分析以获得滤波器回路数学模型。滤波器电路如图1所示。

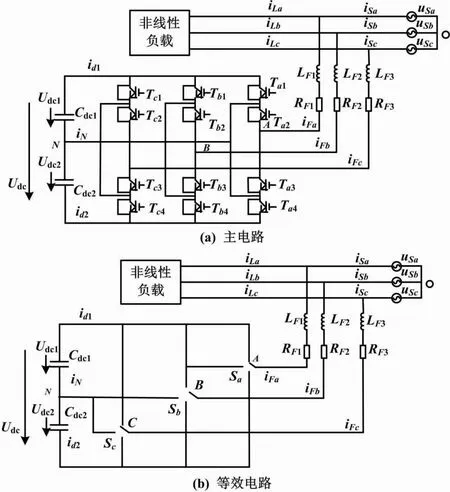
图1 滤波器电路图

主电路采用了二极管钳位变流器的拓扑结构。该结构由桥臂、绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)开关管、续流二极管和钳位二极管组成。钳位二极管的作用是保证一个桥臂每次只有一个IGBT工作,并且使开关管的电压均衡化。电流互感器在开关管Ti1、Ti2(i=a,b,c)接通时,输出正电压;在开关管Ti2、Ti3(i=a,b,c)接通时,输出零电压;在开关管Ti3、Ti4(i=a,b,c)接通时,输出负电压。该负电压使变流器输出所需的补偿电流,以便后续控制电网谐波补偿。

由图1(a)可知,以二极管钳位式变流器为基础的有源电力滤波器,其主回路比较复杂。这不利于后续控制的实现。为了便于分析和控制,必须构建一个以开关函数为基础的数学模型。该模型本质上是一个对系统的理想等值[8],但不考虑开关管的换流过程和电路损耗情况。这是构建和分析其他数学模型的先决条件[9]。在有源电力滤波器的主电路架构中,本文假定三相网压对称并不发生失真、每一桥臂上的开关管均为理想的开关装置。因为有源电力滤波器的每个相位均可输出三相电平,所以可以把每个相位等效为单侧三投式开关,得到如图1(b)所示的滤波器等效电路。

图1(b)中:uSa、uSb和uSc为三相电网电压,V,三者均对称;iFa、iFb和iFc为三相有源电力滤波器输出的补偿电流,A;Cdc1和Cdc2为用于直流侧电压平滑处理与减小直流侧脉动电压的变流器指流端电容[10-11],F,Cdc2=Cdc1;Udc1和Udc2分别为该变流器指流端的两端电压,V;id1和id2分别为在该变流器指流端流动的控制系统输出的电流与反馈测量获得的真实电流,A;LF1、LF2、LF3为有源电力滤波器电网侧与负载侧输出的等效电感[12],H;RF1、RF2、RF3为有源电力滤波器电网侧与负载侧输出的电阻,Ω。

在有源电力滤波器主回路中,各相均可输出三个电平,并与三个不同的状态相对应。那么,对于a相桥臂,开关函数Sa为:

(1)

本文将开关函数Sa分解成三个开关函数Sa1、Sa2、Sa3,分别对应式(1)中三种不同情况,并且将开关管Ta1对Ta2的开关函数定义为Sa1。如果Ta1与Ta2相导电,则Sa1=1;如果Ta1和Ta2关断,则Sa1=0。本文将开关管Ta3和Ta4的导通状态定义为Sa2。如果Ta3和Ta4相导电,则Sa2=1;如果Ta3和Ta4关断,则Sa2=0。

由以上分析可得,当Sa=1时,Sa1=1、Sa2=0、Sa3=0;当Sa=0时,Sa1=0、Sa2=0、Sa3=1;当Sa=-1时,Sa1=0、Sa2=1、Sa3=0。与此相似,开关函数也能用另两个相位来定义。

根据有源电力滤波器主回路的构成,并结合基尔霍博电压法[13],能够获得输出电压与补偿电流表达式。

(2)

式中:uaO、ubO、ucO分别为三相线路的有源电力滤波器的输出电压,V。

根据图1(a)可知,三相电压与变流器直流端的输出电压在式(2)中被直接给出,以便后续解耦控制。而其电容电压之间存在着如式(3)所示的直接联系。

(3)

根据基尔霍博电流规律,并结合有源电力滤波器的主要电路,可以得出有源电力滤波器直流端的两个电容器电流表达式。

(4)

将式(2)、式(4)相结合,可以获得三相静止abc坐标下开关函数的滤波器模型。该模型是对一个真实有源电力滤波器系统的数学描述。模型中的参数变量较多。这些变量之间的相互耦合性强,使得滤波器难以调节输出电流。因此,本文将该模型与电力电子坐标技术[14-15]融合,将三相变为两相dq坐标系,令谐波控制变量和耦合性变小,以便后续分析和控制。在变换过程中,本文引入等功率转换,使得系统中的信号在不同坐标系之间进行转换时能保持功率不变,从而减小各信号之间的耦合效应。转换矩阵为:

(5)

对于转换矩阵,θ=wt+θ0。其中:w为一个空间向量的自转角;θ0为三相空间向量与三相abc坐标系之间的角度。由转换矩阵变换后,获得两相旋转dq坐标系有源电力滤波器模型输出电压和补偿电流、两电容电流。

(6)

式中:iFq、iFd分别为dq坐标系三电平有源电力滤波器的输出补偿电流,A;Sd、Sq分别为dq坐标系的两个开关函数;usd、usq分别为dq坐标系变换后两相的电网电压,V;ud、uq分别为dq坐标系有源电力滤波器输出电压,V。

(7)

通过补偿电压和电流可以有效降低谐波的影响。式(6)、式(7)将为进一步研究有源电力滤波器的可逆特性、实现有源电力滤波器的解耦控制、降低算法复杂度、提高算法效率奠定理论基础。

2 有源电力滤波器可逆性设计

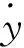
(8)

式中:udc为直流两端总电压,V;ω为基本波的角速度。

(9)

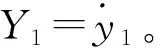
(10)

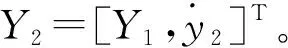
(11)

(12)

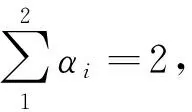
(13)

式中:φ为系统输出方差。

本文进一步设输出变量Y=[y1,y2]T,那么Y关于x的雅可比矩阵的行列式为:

(14)

通过对隐式函数的分析,x可以用Y的函数来表示,也就是x=ζ(y1,y2)。其中,ζ为隐含谐波。替代式(13)后能够获得:

(15)

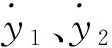
(16)

一个系统模型的逆系统输出变量和输入变量的标准格式为:

(17)

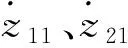
通过并联逆系统,可以实现有源电力滤波器在旋转坐标下的线性化、加强各补偿电流成分之间的解耦,从而降低谐波。

3 有源电力滤波器PI解耦控制

PI解耦控制是降低谐波的重要方法。本文基于瞬态无功与旋转坐标变换的谐波补偿PI解耦控制技术,假定三相负载均衡,并使三相固定坐标系中的k次正序谐波电流向两相固定坐标系转换,以获得一个沿逆时针方向转动、角速度为kω的向量。将这一向量转换到与其角速度和方向一致的坐标系下,并经过带通滤波器获得谐波的幅值,即可实现对谐波的解耦。在此基础上,本文以各次谐波的幅度为输入,实现对全部谐波的解耦控制。

基于谐波补偿解耦控制的电流环等效模型如图2所示。

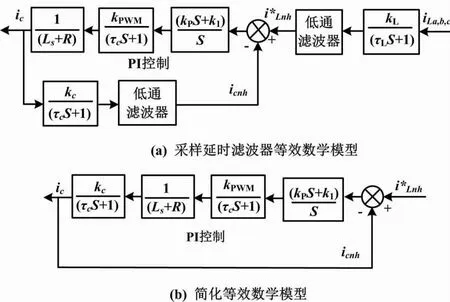
图2 基于谐波补偿解耦控制的电流环等效模型

图2(a)是考虑到样本延迟时,s域下有源电力滤波器的等效数学模型。其中:kP为比例增益系数;kI为积分时间常数;kL为电流传感器变比;τL为输出电流和负载电流采样延迟。

在稳定状态和带通滤波器输出下,通过坐标转变后,各次谐波的振幅均保持不变。假定负载电流与有源电力滤波器输出电流采样延迟与电流传感器变化率一致,即输出电流和负载电流采样延迟τc=τL、电流传感器变比kc=kL,则可以将图2(a)简化为图2(b)。

此模块的开环传递函数Gol(s)的表达式为:

(18)

式中:τs为输出延迟时间,s;kPWM为放大倍数;kif为电流传感器变比。

由式(18)可知,本文滤波器系统是I类系统。该系统被设定为解耦后的各次谐波振幅,且在稳定时为一个恒定的量。因此,该系统能够对电流完成无差PI解耦控制,以降低谐波。

4 试验分析

为了检验所提技术的正确性和有效性,本文在实际电网中进行测试。

试验采用了某市三相交流电220 V/50 Hz的电网,利用Matlab/Simulink软件模拟有源电力滤波器的等效电路。其中:滤波器的交流端有1 mH的电感和0.1 Ω的等效电阻;主电路逆变器的直流端电容为1 200 μF;直流端的基准电压为700 V。试验负载包括三相全控桥式整流电路,以及负载电阻和电感。

未采用控制技术的响应波形如图3所示。

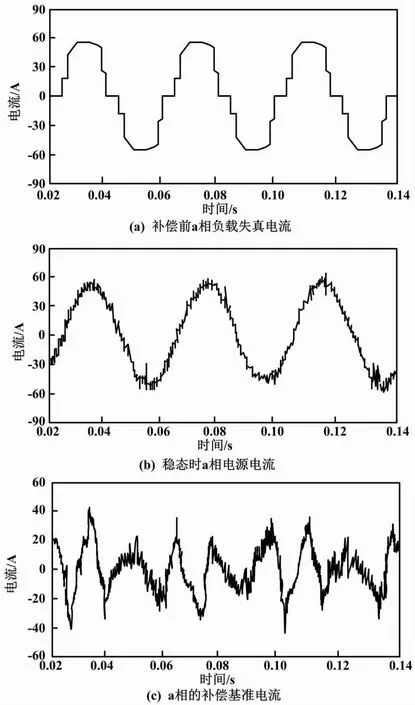
图3 未采用控制技术的响应波形

由图3(a)可知,系统中的电流失真较严重。图3(a)的波形中包含了许多高次谐波成分,谐波失真高,影响了电力系统运行。由图3(b)和图3(c)可知,当补偿基准电流发生了迅速变化时,因为未采取控制措施,致使电流发生失真现象,所以滤波器的运行效果较差。

试验采用本文所提技术对图3所示的响应波形进行控制。采用所提技术控制的响应波形如图4所示。

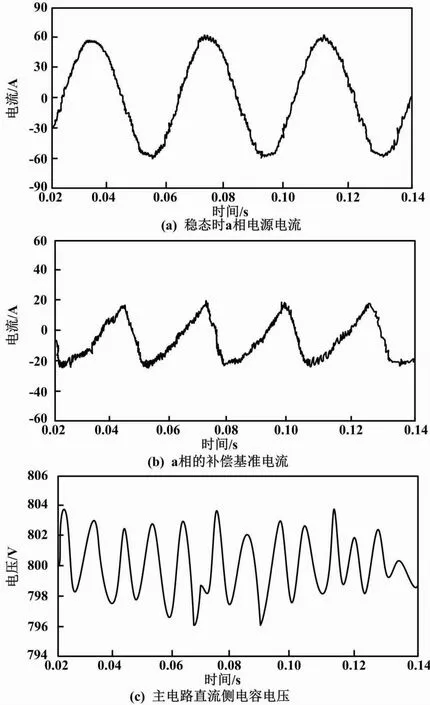
图4 采用所提技术控制的响应波形

由图4可知,采用所提技术控制下有源电力滤波器可以有效补偿电网中的失真电流,使电网中的电流表现为正弦波。根据系统中的实际补偿电流能够很好地掌握基准电流的变化。两者之间的差别不大。同时,主回路中的直流侧电容电压也能够保持在规定的水平。

比较图3与图4可知,利用所提技术进行控制可以实现对有源电力滤波器的谐波补偿。

为了对所提技术的解耦性能进行验证,试验在0.085 s时,对q轴的跟踪基准电流添加一个阶跃信号扰动。所提技术下基准电流突加阶跃扰动时响应波形如图5所示。由图5可知,由于q轴跟踪基准电流的变化,使得q轴的实际补偿电流发生了变化。但是该变化并不会对d轴的实际补偿电流造成影响,并且只有在基准电流的阶跃下才会对有源电力滤波器的滤波性能造成一定的影响。由上述分析可知,所提技术可以使有源电力滤波器中的谐波电流成分得到充分的解耦。

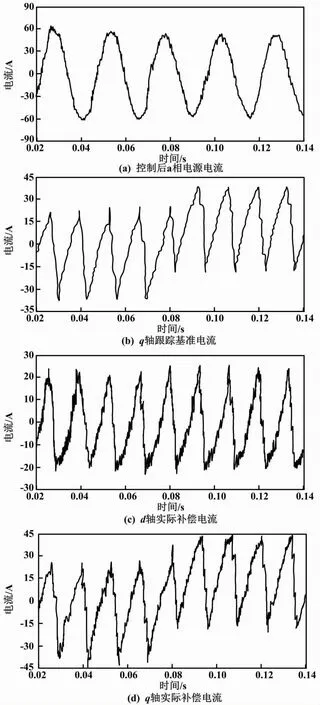
图5 基准电流突加阶跃扰动时响应波形

5 结论

电力系统中越来越多的非线性负载,使得内部谐波问题变得更加复杂。本文设计了有源电力滤波器。有源电力滤波器是一种能够动态地过滤谐波的电力设备,在电网中的应用日益广泛。本文通过电力滤波器建模,研究其内部构造和可逆性,得到旋转坐标线性化特征;采用瞬态无功和旋转坐标变换方式,将谐波幅度输入其中,从而达到谐波电流解耦控制。试验结果表明,所提技术控制能够实现对有源电力滤波器中的谐波电流解耦、补偿电网中的失真电流,从而保证电力系统的正常运行。