转盘偏心距对不对中-碰摩转子动力学响应的影响

2024-05-07张凌云李銮贺晓莹刘忠熊中刚

机床与液压 2024年6期

张凌云，李銮，贺晓莹，刘忠，熊中刚

(1.桂林航天工业学院机电工程学院，广西桂林 541004；2.桂林航天工业学院广西特种工程装备与控制重点实验室，广西桂林541004；3.福建船政交通职业学院汽车学院，福建福州 350007)

0 前言

电机与转子通过齿式联轴器相互连接，因此产生的不对中故障是转子系统众多故障类型中较为常见的一种[1]。掌握多种故障耦合条件下旋转机械的非线性动力学特性，对设备进行预测诊断具有重大的理论意义和工程应用价值。

国内外学者针对不对中-碰摩耦合故障的发生机制和复杂现象进行了一系列研究。文献[2-3]对不对中故障旋转机械的安全运行进行了研究。肖汉等人[4]利用有限元法研究了非线性油膜力影响下不平衡-不对中-碰摩耦合故障的滑动轴承-转子系统动力学模型，通过微分耦合模态对多重故障耦合条件下的频率响应叠加形式进行分解，为多种耦合故障下的复杂系统求解提供了理论基础。BOUAZIZ 等[5]以不对中故障转子系统的动力模型为研究对象，研究结果表明：存在角度不对中故障转子系统的频谱图响应主要由2倍频和4倍频成分组成。PENNACCHI等[6]通过分析不对中转子轴心轨迹响应呈现出“8”字形的特点，揭示了该类转子系统的一些非线性动力学行为。韩捷、石来德[7]基于齿式联轴器不对中的理论分析，建立联轴器外壳质心、瞬心以及啮合线的运动方程，提供了齿式联轴器不对中故障特征识别以及频率特征故障提取的理论依据。钟志贤等[8]以滚动轴承支撑的多故障转子为有限元模型，通过一系列响应图分析了多故障耦合转子运行过程中的故障特征。佘斌等人[9]通过试验分析了联轴器角度不对中工况下转子系统的动力学响应特征，并与理论仿真进行了对比分析。

综上所述，以往的研究只考虑了转子的周期运动和临界转速，未对发生碰摩的轨迹进行识别，也未对转子系统发生碰摩的时间占比进行考虑。本文作者研究转子系统在不平衡力、油膜力、齿式联轴器不对中-转盘碰摩共同作用下的非线性动力学响应特性，采用变步长Runge-Kutta数值积分法进行数值求解。同时，通过最大碰摩力和占空比对系统发生碰摩冲击的严重程度和占比进行量化表征。最后，通过改变转盘主要参数偏心距e，辨识系统参数对转子系统动力学响应的影响，得到转子系统参数与系统周期运动合理的匹配区间。

1 系统动力学模型

考虑齿式联轴器不对中-碰摩耦合故障模型如图1所示，质量均考虑集中质量，转盘两侧通过对称结构的滑动轴承支撑。其中：O为参考系中心；O1为轴承内径几何中心；O2为转盘几何中心；m1为转盘集中在轴承处的质量；m2为转盘集中质量；c1为轴承阻尼系数；c2为转盘阻尼系数；e为转盘偏心距；转轴为刚度系数k的柔性轴；kc为碰摩刚度；δ1为转盘与定子的径向间隙。

图1 滑动轴承-转子系统模型

1.1 不对中-碰摩耦合转子系统动力学方程

设左端轴颈的径向位移为X1和Y1，转盘的径向位移为X2和Y2，通过 Lagrange 方程确定不对中-碰摩耦合故障作用下转子系统的动力学方程为

(1)

式中：PX2、PY2为碰摩力；FX1、FY1为轴承油膜力；FZX、FZY为不对中产生的作用力；g为重力常数；ω为转子的角速度(左视图顺时针为正转)。

1.2 非线性油膜力

文中所研究滑动轴承采用非线性较好的Capone短轴承的油膜力模型[10]，该模型的收敛性和精度较好。

量纲一化后的油膜力：

(2)

式中：σ为Sommerfeld修正系数。

(3)

式(3)中各参数表示为

(4)

式中：μ为润滑油黏度；c为轴承间隙；x1和y1分别为轴承的内径几何中心在X轴方向和Y轴方向的位移。

1.3 碰摩力模型

图2所示为图1转子系统的左视图。转盘中心的初始位置为O，该转子系统运行时，当转盘径向位移δr>δ1时，转盘与定子产生碰摩作用，碰摩过程中产生径向力Pn和切向力Pt可以表示为

(5)

图2 碰摩力模型

将以上碰摩力分解到X轴方向和Y轴方向分别为

(6)

1.4 齿式联轴器不对中模型

此齿式联轴器模型考虑综合不对中，其作用力模型如图3所示。

图3 齿式联轴器综合不对中作用力模型

图3中联轴器外壳与两半联轴器间存在相对运动。设点A为电机主轴的轴心投影，点B为转子转轴的轴心投影，点C为外壳的动态中心，AC为外壳与电机主轴的连线，BC为外壳与转子转轴的连线，AC垂直BC。设AB长为ΔE，点C坐标为C(x,y)，夹角不对中量为α，则当转子系统运转时，点C以综合不对中量ΔE为直径做圆周运动，ω为转速，则点C的坐标可表示为

(7)

综合不对中量ΔE由联轴器间距ΔL、平行不对中量ρ以及不对中夹角α共同决定：

ΔE=ρ+ΔLtanα/2

(8)

随后，由式(7)对时间t求二次导数，得到点C的加速度，即：

(9)

由式(9)可知，当联轴器存在不对中故障时，将会给转子系统施加一个额外的激振力F。若将其在o0-x和o0-y方向上做投影，其分量满足：

(10)

为了进行系统的动力学研究，引入以下量纲一化参数：xi=Xi/b(i=1,2)，yi=Yi/b(i=1,2)，τ=ωt，则式(1)可化为

(11)

2 数值仿真与分析

2.1 最大碰摩力与占空比

文中引入最大碰摩力和碰摩占空比来表征转子与定子碰摩的激烈程度和持续时间。最大碰摩力表述了转盘与定子在接触过程中产生的最大作用力，碰摩作用是导致转子系统出现异常振动的非线性因素之一，是决定轴承-转子系统使用寿命的关键参数。文中将最大碰摩力定义为：在一个运动周期Tn=2nπ/ω内，转盘与定子水平竖直方向碰摩力合力的最大值，表示为

最大碰摩力的取值为Pmax≥0。另外引入电信系统中的“占空比(Duty Cycle)”，文中用δDC表示碰摩占空比，即转子在一个运动周期Tn=2nπ/ω内，转盘与定子在各接触阶段所耗费时间的总和与运动周期的比值，表达式为

δDC=(ΔtDC1+ΔtDC2+ΔtDC3+…)/Tn

其中：δDC∈[0,1)。

2.2 系统的Poincaré截面

文中采用p/n来研究系统的动力学特性，其中p表示转子系统在一个振动周期Tn=2nπ/ω内的转盘与定子的碰撞冲击次数(p=0,1,2,3,…)；n表示转子在一个振动周期Tn=2nπ/ω内的旋转周期数(n=1,2,3,…)，反映在周期分岔图。为了研究不对中-碰撞耦合转子系统的动力学行为与分岔特性，选择系统的Poincaré映射图截面[11]：

R8×T|mod(t=2π/ω)}。

基于表1所示的系统参数，采用四阶变步长Runge-Kutta数值积分法对方程组(11)进行积分求解，为了得到稳定的响应数值，舍去前500个周期的仿真结果，得到系统的一系列响应图。

表1 系统主要参数

2.3 不对中-碰摩耦合转子随转速变化响应分析

为了研究不对中-碰摩耦合条件下转子系统的动力学行为，基于系统参数仿真得到不对中-碰摩耦合转子的响应图，如图4、5所示。其中，图4所示为不同转速对应的响应图，图5所示为系统转速范围内最大碰摩力和占空比分布。

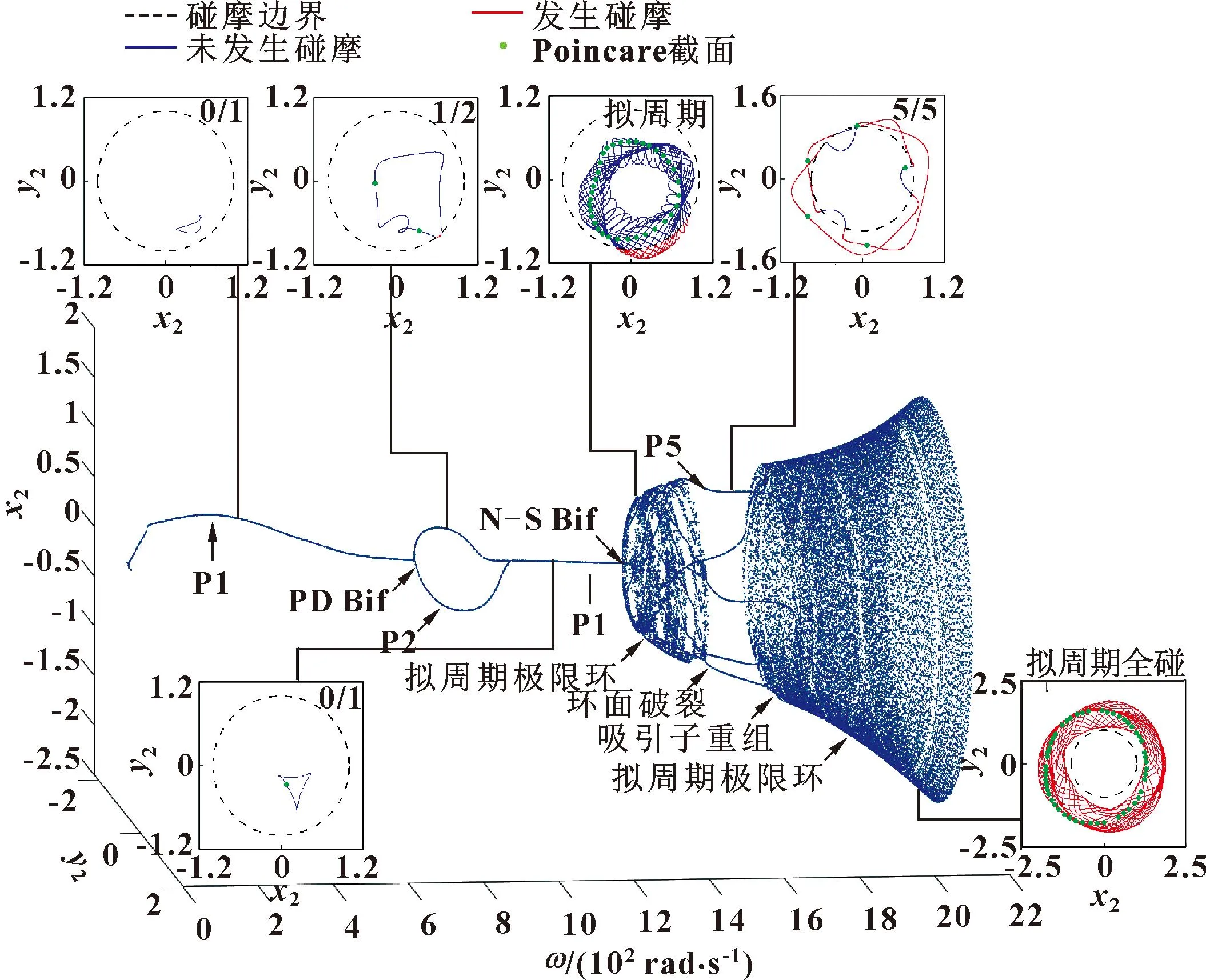
图4 系统分岔图及不同转速对应的响应图

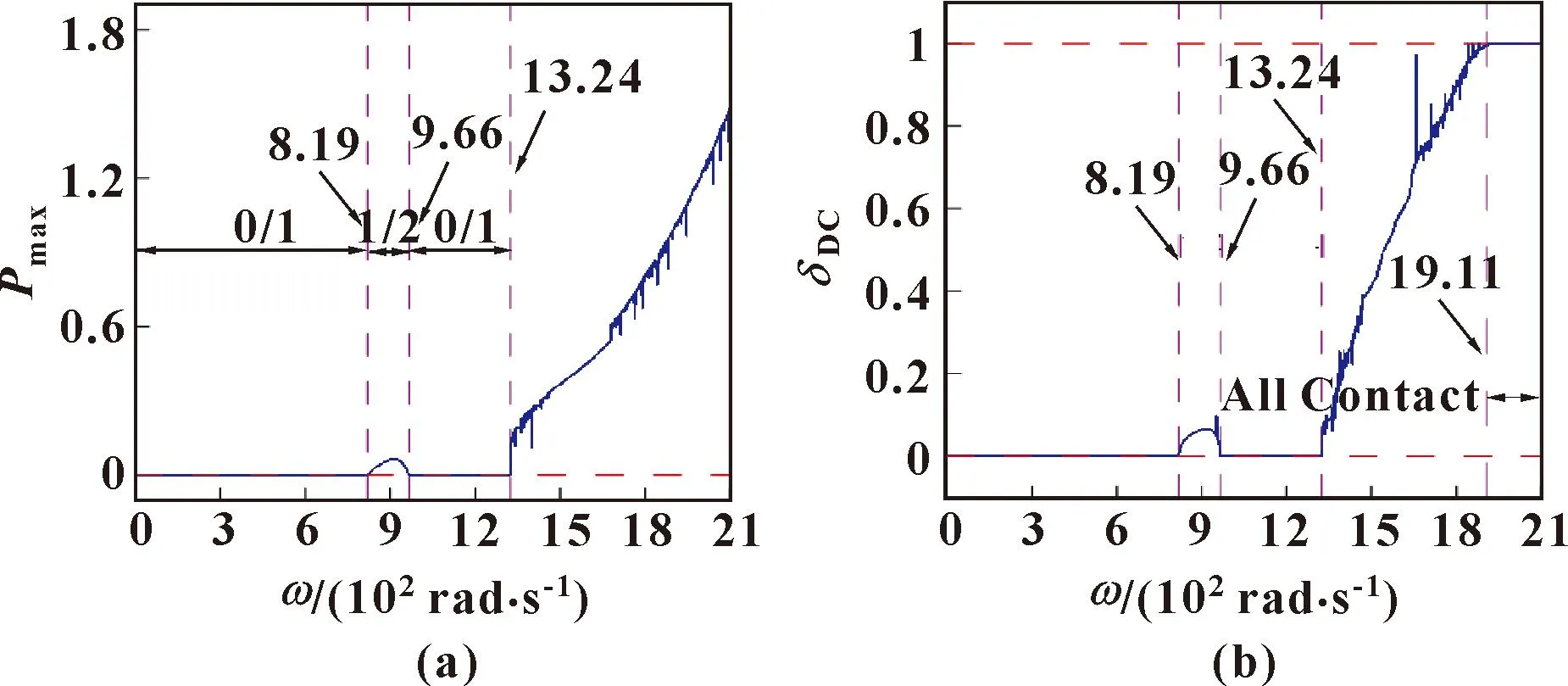
图5 系统最大碰摩力(a)和占空比(b)随转速变化分布

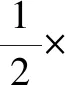
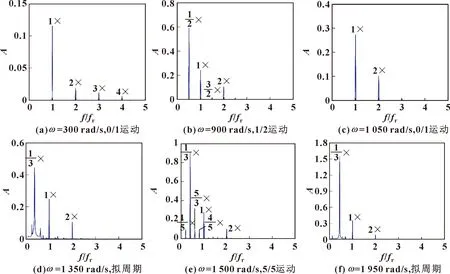
图6 不同转速对应的频谱图

2.4 改变偏心距对转子系统动力学响应的影响

由式(1)可知：转子偏心距e的改变会对转子系统产生直接影响，因此对转子偏心距e=0.05 mm和e=0.1 mm进行离散取值。计算不同e值对应转子系统的周期分岔图、最大碰摩力和占空比随转速改变的分布如图7、8所示。同时，结合图4中e=0.025 mm进行对比分析。转子偏心距e由小变大时，转子系统的分岔特性变得简单化，系统的振动幅值呈现先减小后增大的趋势，同时偏心距的增大使得转子系统的一、二阶临界转速增大。当偏心距e=0.05 mm时，通过图7可知系统的振动幅值呈现连续变化的趋势，并未出现δDC=1的全周期碰摩区域，系统在整个转速窗口内可平稳运行。当偏心距e=0.1 mm时，转子系统在整个转速窗口内呈现周期运动，同时转子的振动幅值变化很大，在较大转速范围内出现了δDC=1的全周期碰摩运动，特别是在一阶临界转速前后，系统发生了跳跃分岔，导致最大碰摩力变化剧烈，严重威胁转子系统的平稳运行和使用寿命。

图7 e=0.05 mm时周期分岔图(a)、最大碰摩力(b)和占空比(c)分布

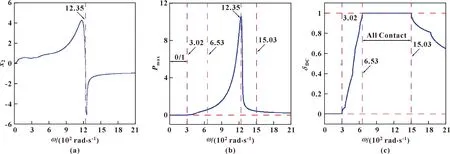
图8 e=0.1 mm时周期分岔图(a)、最大碰摩力(b)和占空比(c)分布

通过以上分析可知，偏心距的改变对系统的运动分布和幅值有显著的影响，为了更直观地说明偏心距对转子系统动力学响应的影响，在转速ω=900 rad/s和ω=1 950 rad/s条件下，分别得到偏心距离散取值e=0.25 mm、e=0.05 mm和e=0.1 mm的相应频谱图，如图9所示。观察图9(a)可知：偏心距较小时，系统的运动类型和分布主要受油膜涡动和油膜振荡影响而发生转迁；当偏心距逐渐增大时，系统转频分量占据主导，同时能有效地抑制油膜力的影响，进而使系统运动趋于稳定，但偏心距的增大会导致一阶临界转速范围内系统转频的幅值急剧增大，而不会影响不对中产生的2×频率幅值。

图9 不同偏心距对应的频谱图

2.5 定转速下偏心距对转子系统动力学响应的影响

分析第2.4节分析可知，转子的偏心距e变化对系统运动类型、存在区域和分岔特性有较大影响。因此在转速ω=900 rad/s和ω=1 950 rad/s下，得到偏心距持续改变对转子系统动力学响应的影响如图10、11所示。当ω=900 rad/s时，如图10(a)所示，沿着偏心距e增大的方向依次经历了P1-P2-P1运动，并且在e=0.065 mm时发生了跳跃分岔，系统的振动幅值急剧增大；通过图10(c)可知系统进入全周期碰摩状态，对应图10(b)的最大碰摩力发生突变，说明偏心距e≥0.065 mm系统发生严重的全周期碰摩，进而影响转子在该转速范围内运行的平稳性。

图10 ω=900 rad/s时周期分岔图(a)、最大碰摩力(b)和占空比(c)分布

当ω=1 950 rad/s时，如图11(a)所示，沿着偏心距e增大的方向依次经历了拟周期-P5-拟周期-P1运动，系统的振幅呈现先减小后增大的趋势，同时对应的最大碰摩力和占空比整体同样先减小后增大变化。当偏心距离e在(0～0.027) mm时，由于油膜振荡占据主导作用，导致系统的振幅较大，此时通过图11(c)可看出系统处于δDC=1全周期碰摩状态。当e=0.068 mm时，系统通过Hopf Bif退出拟周期进入P1运动，观察图11(b)可知，系统偏心距离e在(0.068～0.08) mm时处于0/1无碰摩冲击运动状态。当偏心距进一步增大时，系统的振幅持续增加，进而进入碰摩力和占空比持续增大的P1运动。结合上述分析可知，偏心距能有效抑制油膜力对系统稳定性的影响，但过大的偏心距导致系统一阶临界转速范围内的振动幅值急剧增大，不利于系统的平稳运行。综上可知：此模型的偏心距e取值为(0.027～0.065) mm时，既能减小油膜力对系统稳定性的影响，同时在整个转速范围内系统的幅值和对应的最大碰摩力及占空比持续变化，进而降低响应突变的影响。