氟金云母陶瓷材料铣削温度预测模型及试验研究

蒋涵存，马廉洁，2，李文博，孙杨，韩智斌，谭雁清，李明

(1.东北大学秦皇岛分校控制工程学院，河北秦皇岛 066004；2.东北大学机械工程与自动化学院，辽宁沈阳 110819)

0 前言

切削温度作为铣削加工中的重要特性，一直是重要的研究对象[1]，会直接影响工件表面质量和刀具寿命。工程陶瓷材料具有良好的力学性能和化学稳定性且机械强度高、耐磨性好等，广泛应用于军工、核能和生物医学等高新技术领域[2-3]。氟金云母作为工程陶瓷的一种也被广泛应用于各种领域，相比其他工程陶瓷，它具有容易切削的特点，且具有和碳钢类似的加工性能，但由于其高硬度和脆性，使得它在切削加工中有一定的困难，目前对其切削加工性能方面的研究较少[4]。而切削热作为切削加工过程中重要因素之一，易引起刀具磨损以及影响工件性能，从而影响刀具寿命和工件的使用性能，降低了加工效率的同时使得加工成本提高，因此对切削过程中的切削热及切削温度进行研究具有重要意义[5-6]。

马廉洁等[7]通过试验研究了进给量和切削深度对第二次跃迁温度的影响，并验证了建立的脆性材料切削热传导理论模型的正确性，可以反映陶瓷等脆性切削温度场的变化趋势。赫培等人[8]首先建立切削温度理论模型，通过热源法进行单因素试验得到温度随各参数的变化趋势，可以在脆性去除范围内预测切削温度随工艺参数的变化趋势。邓星等人[9]通过试验与响应面法研究得出了TC4钛合金铣削温度随铣削参数的变化趋势，并对温度值进行优化得到最佳加工参数。1943年，JAEGER[10]提出了移动热源法。刘具龙等[11]以热源法为理论基础建立了基于热源法的工件温度场解析模型，基于该数学模型可计算出不同加工参数条件下工件表面的铣削温度理论值。铣削温度的测量在切削加工中的地位十分重要，红外测温仪具有响应速度快、不易破坏原有物体温度场分布、可测量的温度范围广和分辨率高等特点，因此广泛应用于各种温度测量的场合，成为切削过程中重要的测温手段之一[12-13]。

本文作者建立氟金云母陶瓷铣削过程中关于每齿进给量、铣削速度、铣削深度和铣削宽度4种加工参数与铣削温度的数学模型，为氟金云母陶瓷铣削温度预测提供参考。通过单因素试验对数学模型进行验证，分析铣削工艺参数对铣削温度的影响规律。

1 解析法求解铣削传热模型

1.1 铣削过程热量来源

对于铣削加工而言，切削过程中切削热主要由三部分产生，如图1所示，分别是：工件与刀具间的剪切变形区、切屑与前刀面的摩擦热源区和工件与后刀面的摩擦热源区，其中大部分热量被切屑带走，其余热量主要流入到工件和刀具中。

图1 切削热产生原理

研究目标主要是刀/件摩擦热源区的温度变化，该热源区热量的主要来源是由刀具后刀面与工件表面之间相互摩擦产生的摩擦热。针对氟金云母陶瓷材料铣削过程中的工件表面温度进行建模，建立工件表面温度场解析模型，对不同加工参数条件下工件表面的铣削温度进行预测。

1.2 铣削温度数学模型

在铣削氟金云母陶瓷材料的过程中，其产生热量的热源具有一定尺寸和形状且不断移动，但由于其边界条件基本是未知的，如果根据传统解析法分析铣削过程的温度场需要设定几何条件和传热条件等要求，因此求解温度场模型比较困难。而热源法可以根据导热微分方程的解先求出瞬时点热源温度场的解析模型，而点热源的不断累积将会形成线热源，线热源又将累积成面热源，所以以点热源的解析模型为基础进行积分，可以求出铣削过程中切削面的温度值。此方法相比传统解析法更为简单，计算结果与实际值较为接近，因此以热源法为基础对氟金云母陶瓷材料铣削过程的温度场进行研究。

各种形状的热源都是由点热源累积而形成的，所以在研究工件表面温度变化规律时，要先从点热源入手，点热源是求解被加工表面传热模型的基础。瞬时点热源是加工过程中切削热瞬间作用在某一点上，使该点具有一定的热量，并且作用在点上的时间足够短、空间足够小，那么可以把这点称为瞬时点热源。各种类型的热源都是由点热源组合而成，因此瞬时点热源温度场是求解被加工工件表面切削温度的基础。切削过程中的工件瞬时点热源温度场模型是根据工件的导热微分方程经过傅里叶变换推出的。

如图2所示，将氟金云母陶瓷工件视为无限大的导热介质，取一个坐标原点视为点热源，在距离点热源R处有一点M(x,y,z)，t=0时点热源发出热量为Q，随后不再发热。点M受到点热源的影响将会产生一定的温度变化，根据点热源的传热模型，可以得到瞬时点热源在工件内对任意一点所造成的温升。温升公式为

(1)

图2 点热源示意

其中：c为氟金云母陶瓷材料比热容；ρ为陶瓷材料密度；α为导热介质的热扩散系数。

一条线段是由无穷多个点排列组合而成的，所以瞬时有限长线热源可以看作是由无数多个瞬时点热源按照直线排列而组成的，以瞬时点热源的传热模型为基础进行积分可以得到瞬时有限长线热源的传热模型。如图3所示，在无线大的导体介质中，有一条长度为L的线热源，其单位长度发热量为q1。

图3 线热源示意

在线热源中任意取一微元线段dzi，由式(1)可知，这一微元线段的瞬时热源对点M处产生的温升可表示为

(2)

对dθ在[0，L]上积分可以得到整个线热源对点M处产生的温升：

θ=

(3)

其中：erf为误差函数。

如图3所示，在无限大的导热介质中，有一热流密度为q的瞬时有限长线热源以速度vf向前移动，在经过t时间后，对点M将会造成一定的温升影响。在线热源移动的整个过程中，可以将移动时间t拆分成无数个微小的单元，其中某个微小的时间单元视为瞬时的。

在移动过程中的ti时刻任取一段微元时间dti，在dti中线热源的发热量为q1dti，点M到线热源的距离为x-vfti，线热源移动到点M所需要的时间为τ。在dti时间内线热源对点M产生的温升为

(4)

对θ在[0，t]上进行积分，可得到运动过程中的线热源对点M产生的温升：

(5)

1.3 工件表面传热解析模型

文中对工件都是通过刀具的侧刃进行切削的，图4所示为加工过程中的工件表面加工状态，阴影部分为铣刀切削工件时的加工表面及发热面。

图4 铣削过程原理

铣刀加工陶瓷工件的切削过程就相当于一个位置不断发生变化的面热源对工件表面加热的过程，而刀具的铣削速度是远远大于进给速度的，因此为了方便计算可近似地认为该表面是一个沿着进给方向、以进给速度vf运动的弧状面热源。由此可算出：

(6)

其中：L为面热源的弧长；R为铣刀的刀具半径；ae为铣削宽度。

切削工件时热源单位时间内的发热量Q=Ftv，Ft为工件受到的切向力，v是铣削速度。Rm为热量传入工件的比例系数，由此可得出热流密度：

(7)

面热源可以看作是由无数条的移动有限长线热源组合而成的，取其中任意一条线热源进行分析，将线热源对点M处造成的温升在[0，L]上进行积分，即可得到面热源对点M产生的温升公式[14]为

(8)

1.4 热量分配比例系数

在建立的面热源对点M产生的温升公式中，若想准确地求出铣削过程中的温度值，除了需要准确地计算积分以外，对于热流密度q的计算也较为重要。q计算的关键是求出热量流入工件的比例系数Rm，但Rm与工件刀具的材料属性、接触面积和加工参数等有一定关系，研究起来具有一定难度。

目前，在铣削加工中对于热量分配比例系数Rm的研究较少，而在磨削加工中对Rm的研究较多，陶瓷工件的主要加工方式就是磨削加工，所以参考磨削的研究方法对铣削氟金云母陶瓷具有一定的价值。砂轮上磨粒之间具有一定的间隙，而且铣刀上刀齿间同样具有一定距离，所以铣刀切削工件时与磨粒对工件产生划擦和挤压具有类似的作用，且铣削与磨削加工材料的尺寸大小和去除机制都具有一定的相似之处，因此可以以磨削加工中的研究方法为理论基础来计算氟金云母陶瓷材料的热量分配比例系数。

ROWE[15]在研究磨粒与工件相互作用的基础上，建立了热量分配比模型。通过类比磨削加工，结合铣削加工时刀具与工件表面接触宽度和磨削加工时磨粒与工件的有效接触半径类似这一特点，对ROWE的模型加以改进，由此可以得到铣削加工热量分配比例系数的数学模型：

(9)

其中：bD为铣刀刀刃与工件接触宽度，bD=fzsinθ，θ为铣刀螺旋角；λg为刀具导热系数。

2 氟金云母陶瓷铣削试验

2.1 试验条件

此试验是在TC500R立式加工中心上完成的，并采用Kistler9119AA2型测力仪完成铣削过程中切向力的测量；采用型号为FT-H10C的红外热像仪对工件表面进行测温，将它安装在机床主轴侧边使其尽可能对准工件的加工区域内，将采集到的信号输送到计算机中对温度信号进行处理和保存。

图5所示为试验加工现场工艺系统。选用形状为45 mm×20 mm×10 mm长方体的氟金云母陶瓷为切削材料，材料的性能参数如下：物体比热容c为0.185 J/(g·K)，物体密度ρ为2.45 g/cm3，导热系数λ为2.1 W/(m·K)，热扩散系数α为4.633 m2/s。试验所使用的刀具是直径为8 mm三齿立式硬质合金铣刀，其导热系数λg为50 W/(m·K)。

图5 加工现场工艺

2.2 试验方案

为了研究不同加工参数对加工过程中的铣削温度的影响，设计了单因素试验进行探究，通过改变参数的大小得到了其对铣削温度的影响规律。根据工程陶瓷切削理论并结合工程生产实际，合理设计加工参数，如表1所示。

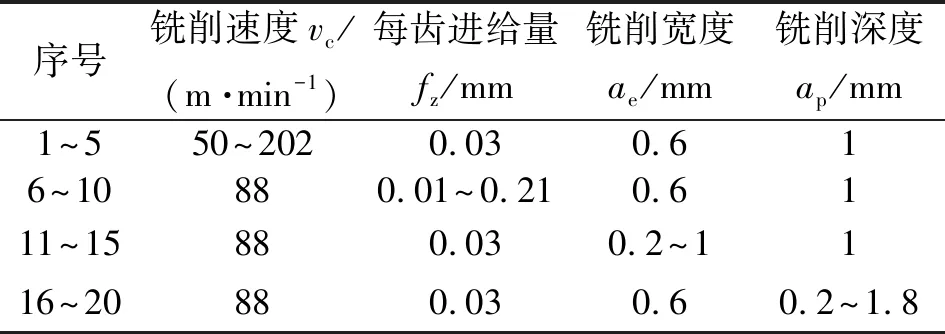
表1 单因素试验参数

3 试验结果分析

3.1 铣削速度对铣削温度的影响

图6所示为氟金云母陶瓷铣削过程中铣削速度对铣削温度理论值和试验值的影响规律。可以看出：随着铣削速度的不断增大，铣削温度也逐渐升高。这是由于随着速度的增加，完成切削所需要的功率不断增加，并且工件与刀具切削刃之间相互摩擦产生的摩擦热越来越多，所以温度逐渐升高。而随着速度的不断增加，温度升高的趋势逐渐变得缓慢。这是由于切削速度变快，热源作用在工件表面的时间变短，作用不充分；另外，由于工件的去除速率提高，热量来不及向工件与刀具传递就被切屑带走，所以温度上升变缓。

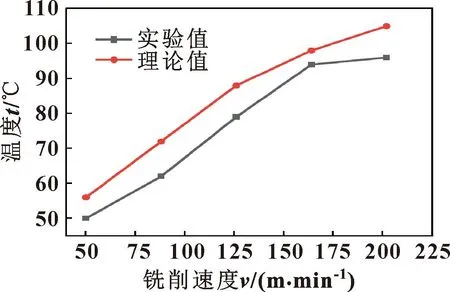
图6 铣削速度对铣削温度的影响

由图6可以看出：铣削温度的理论值与试验值间存在一定的误差，最大误差为10 ℃，最小误差为4 ℃。存在误差是由于计算过程中对模型进行了一些简化，同时将铣削过程中的一些因素视为恒定的，并且采用红外热像仪对工件表面进行测量，这些因素都会使理论值与试验值存在一定的误差。

3.2 每齿进给量对铣削温度的影响

图7所示为氟金云母陶瓷铣削过程中每齿进给量对铣削温度理论值和试验值的影响规律。

当每齿进给量增大时，单位时间内刀具切削工件的体积增大，材料去除率的增加使得切削功率增大，进而使切削温度升高，因此氟金云母陶瓷的铣削温度随着每齿进给量的增大而不断升高。理论值与试验值之间的最大误差为11 ℃，最小误差为1 ℃。

3.3 铣削宽度对铣削温度的影响

图8所示为氟金云母陶瓷铣削过程中铣削宽度对铣削温度理论值和试验值的影响规律。可知：随着铣削宽度的增加，铣削温度逐渐升高。这是因为随着切宽的增加，材料去除体积逐渐增加，切削工件所消耗的功率和克服摩擦做功增大，使切削温度不断升高。理论值与试验值之间的最大误差为5 ℃。最小误差为2 ℃。

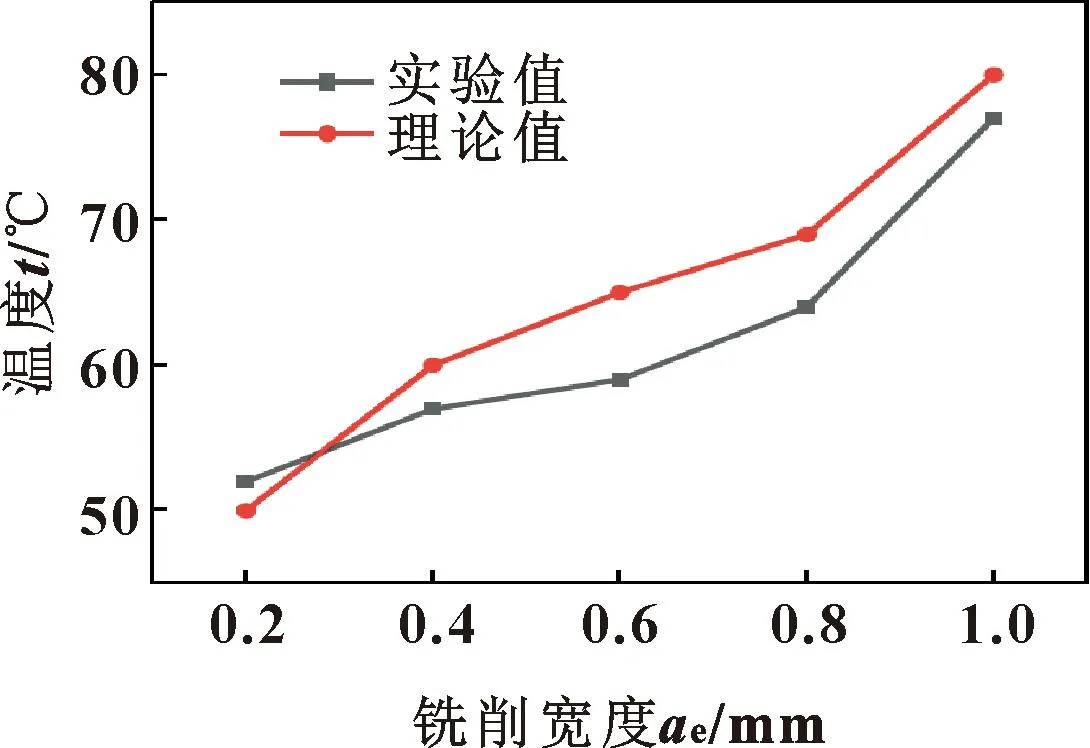
图8 铣削宽度对铣削温度的影响

3.4 铣削深度对铣削温度的影响

图9所示为氟金云母陶瓷铣削过程中铣削深度对铣削温度理论值和试验值的影响规律。

图9 铣削深度对铣削温度的影响

铣削深度对铣削温度的影响与铣削宽度类似，都是由于切削体积增大使得温度升高。由试验及计算结果可以发现，铣削深度对温度的影响最小。原因为随着深度的增加，刀具切削刃与工件间的接触长度增加，散热面积增大，相比其他加工参数，其加工过程中的散热条件较好，能够将热量及时传递出去，留在工件表面的热量减少，所以铣削深度对铣削温度的影响最小。理论值与试验值之间的最大误差为6 ℃，最小误差为1 ℃。

3.5 铣削温度理论值与试验值对比分析

根据以上分析可以得出：氟金云母陶瓷铣削温度的理论值与试验值曲线都呈现逐渐升高的趋势，但两者之间存在一定的误差。通过分析计算及试验过程可得主要原因有以下几点：

(1)为了使公式推导过程方便计算，对一些复杂的铣削过程进行了简化，并且在温度场建模的过程中，将具有一定体积的工件想象成一个无限大导体，这些都会使理论值的计算产生一定的误差。

(2)热量流入工件的比例系数是随着刀具与工件的接触状态随时发生改变的，刀具发生磨损时，热量分配比例系数也会发生改变。然而，在推导热量分配比例系数时，认为切削过程的时间较短，刀具尚未产生磨损，这也会使计算出来的理论值产生一定的偏差。

(3)在铣削试验中，刀具与工件的接触面较小，使得产生温度的热源区域较小，同时由于使用红外热像仪对铣削温度进行测量，无法准确地测量出铣削加工时刀具与工件接触区处的温度值，这些原因也会使测量结果与真实值产生一定的偏差。

4 结论

(1)通过将刀具与工件的材料特性、接触面积和加工参数等因素考虑进热量分配比例系数模型之中，可以在一定程度上提高数学模型预测的准确性，将其代入到氟金云母陶瓷铣削温度场模型中，能够求解出不同加工参数下的铣削温度值。

(2)基于单因素的试验方法获得了不同加工参数条件下的铣削温度试验值和理论值，获得了铣削温度随加工参数的变化规律：任意一个切削参数增加，铣削温度都随之升高。

(3)将氟金云母陶瓷铣削温度的理论值与试验值进行了对比，总体来说两者结果较为相似且趋势相同，解释了2种结果存在差别的原因，对工程陶瓷铣削温度的预测具有一定的借鉴作用。