一项改进小数乘法竖式教学的实验研究
2024-05-06罗永军许兆琛
□罗永军 许兆琛
在小学数学中,存在一些常见且易导致学生出错的问题,这些问题常常被教师戏称为“坑”。尽管教师和学生都对这些“坑”的存在心知肚明,但不管教师怎么提醒,学生还是会不由自主地“掉”进去。例如,受小数加减法竖式计算的影响,学生在进行小数乘法的竖式计算时,往往习惯性地将小数点对齐。然而,小数乘法的竖式计算应当采取末尾对齐的方式。正是这种计算上的习惯,导致学生出现各种错误(如图1)。
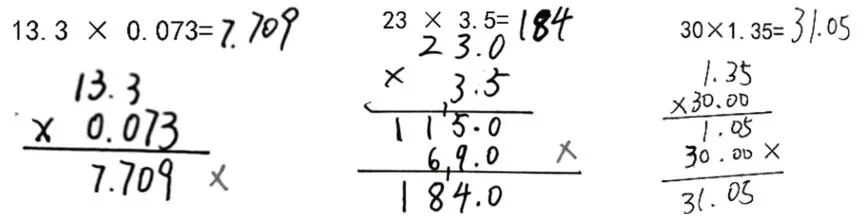
图1
学生出错的原因,与“同形继承”这一既有经验有关。[1]当前的教学主要侧重于通过理解乘法的意义和积的变化规律来理解算理,进而明确算法。尽管算理的理解相对容易,但在实际操作中,由于正处于具体运算阶段,学生的思维依赖可见的具体形式,所以当他们看到小数点时,就不由自主地将其对齐进行运算,从而导致计算出错。此外,受“乘法是越乘越大”(积大于因数)这一经验的负迁移,学生反而会认为错误的结果是正确的。因此,仅仅依靠教师的不断提醒并不能从根本上解决问题。学生的问题就是教学研究的课题,笔者试图重新审视问题的根源,从算理入手,探索破解之道。
一、数学本质的分析
数是对数量的抽象,分析算理需要把数的运算还原为数量之间关系的比较。小数加减法之所以要求小数点对齐或者说相同数位对齐,是由加减法的意义决定的,即表示两个同类量的合并与分离。例如,买了5.7元苹果与4.12元桃子,一共要付多少元?解决这个问题就是要把两个同类量合并成一个新的数量。合并时,要把相同单位上的数合在一起(如图2),5元和4元相加得到9元,7角和1角相加得到8 角,再与2 分相加,得到9 元8 角2 分,即9.82元。这种相同单位上数量的加减运算,抽象到数的加减运算层面,就是相同计数单位的数的加减运算。因此,小数加减法的竖式计算要求小数点对齐。
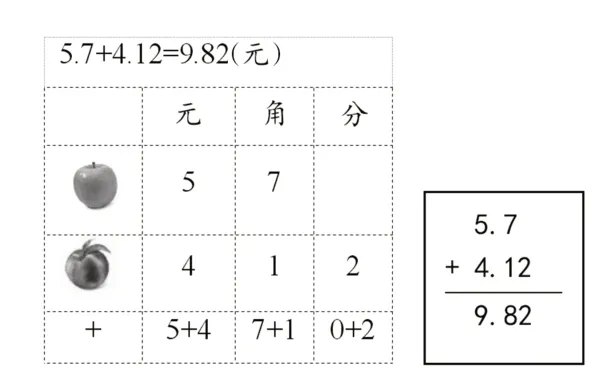
图2
对于小数乘整数的运算,乘法的意义是若干个相同加数相加。因此,当两个因数相乘时,它们所表示的意义是不同的:一个表示“相同加数”,另一个表示相同加数的“个数(倍数)”。例如,买了2千克单价是5.7元/千克的苹果,一共花了多少钱?5.7元/千克和2千克并非同类量,单位也不同。这里的2 需要与5 和7 分别相乘,因此,在进行乘法计算时,并不要求数位对齐(如图3)。
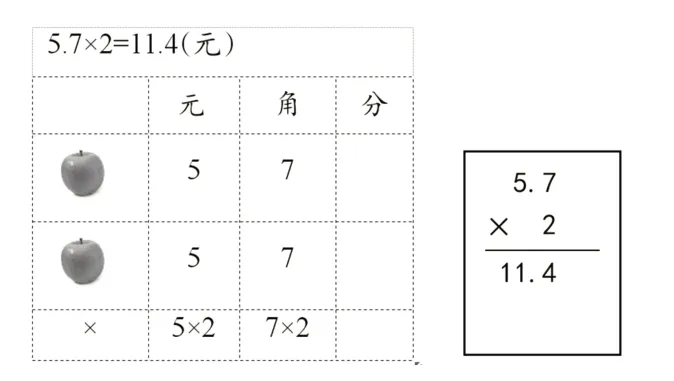
图3
实际上,从计数单位运算的一致性视角来看,可以把5.7元理解为57个0.1元,即57角,而2个57角就是114角。这样,小数乘整数就可以全部转化为整数乘法。这就提供了另一条竖式教学路径,即无须依赖积的变化规律,而是通过“整数化”的方法进行计算,如5.7×2=57×2×0.1=11.4(元)(实际书写时先写结果114,然后再加小数点)。在竖式中,像这样直接按整数乘法的法则进行计算,不加小数点,使得算理和算法得以统一,既易于理解,又便于操作。
那么,对于小数乘小数的运算,是否也可以采用类似的思路进行教学呢?答案是肯定的。其中,乘法的面积模型为小数乘法整数化的算理和算法提供了支持。
二、参考教材的思考
用面积模型解释小数乘法的意义在欧美教材中已经使用多年,如美国的California Mathematics(《加州数学》)。该教材提供了一种让学生直观理解小数乘法意义的方法,这种方法是用方格图来表示小数单位及小数运算(如图4),被称为模型图(Models)。方格图由10×10 即100 个方格组成,表示1;一行或一列10 个方格组成数条,表示0.1 或;每个方格表示0.01或学生三年级第一次认识小数时,便开始使用这一模型图[2],并在后续小数学习过程中反复应用。
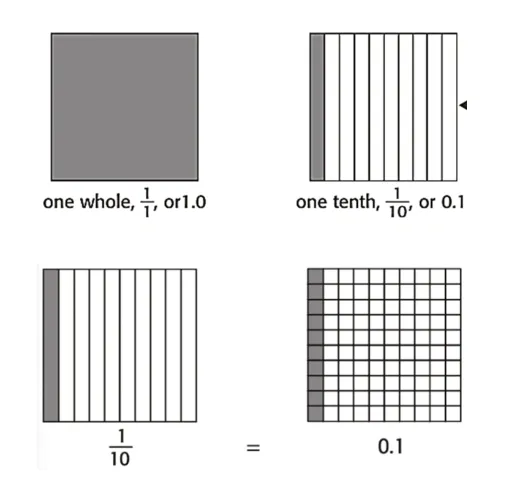
图4
在教学小数乘小数时,教材通过小数模型直观形象地呈现了0.8× 0.4 的计算过程[3]:首先,构建一个10×10 的空白小数模型,每个小方格表示1 个0.01。然后,用涂色表示第一个因数0.8,即每行表示1 个0.1,涂8 行。接着,将模型中的4 列小方格涂成蓝色,表示乘0.4。涂色后的重叠部分即为乘积。这种计算方式实际上是在计算长方形的面积,面积单位与小数单位相对应,即0.8×0.4=8×4×0.01=0.32(如图5)。
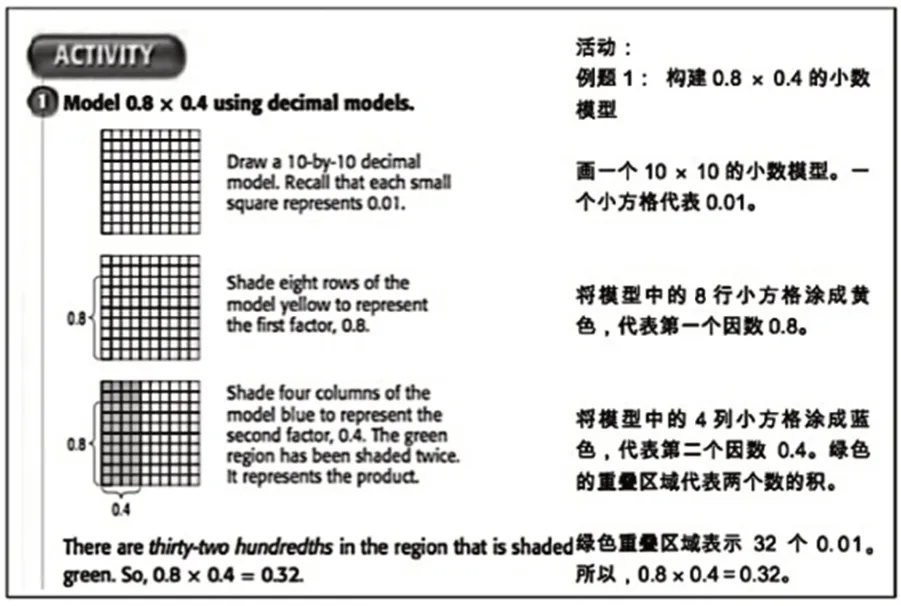
图5
美国教材的编排与笔者的设想不谋而合,除了上述简单的小数乘法,对其他类型的乘法,如0.7×2.5、2.5×1.36、0.036×3500 等,也可以用如下的形式进行计算(如图6)。需要注意的是,在列竖式时,如果涉及小数乘整十数、整百数等的乘法运算,应先化简再计算。
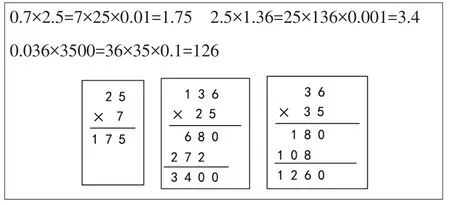
图6
三、学生研究
从运算的一致性视角,把小数乘法整数化,无论是算理还是算法,都是自洽的。此种方法有助于消除学生面对小数乘法时可能产生的混淆和困扰。然而,实际效果究竟如何?为探究此问题,本研究设计了针对小数乘法常见类型的问卷调查(如图7),并进行了对照实验。
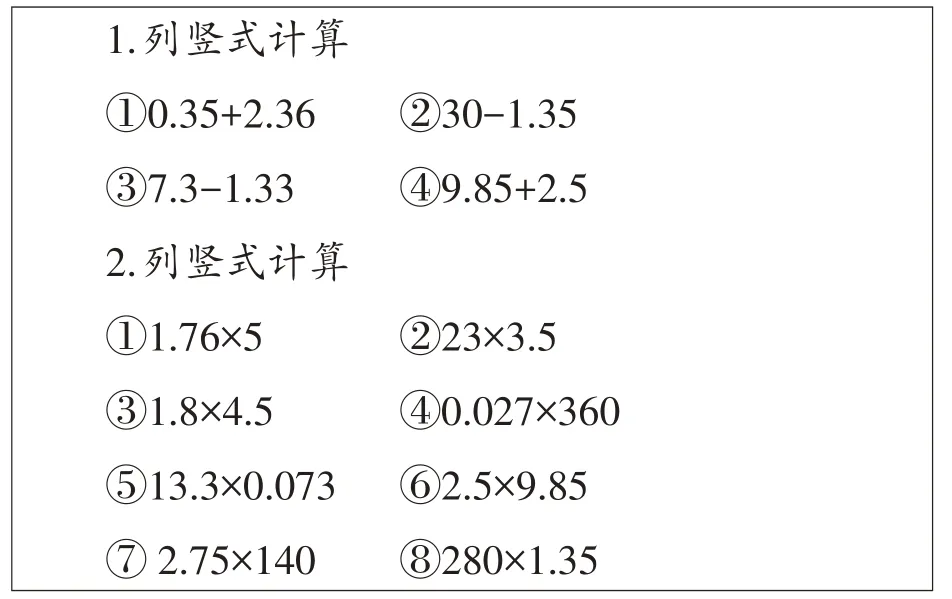
图7
第1部分是小数加减法,共4题,分别涉及了小数加减法的常见类型,以了解学生对数位对齐的掌握情况。第2部分包含小数乘法常见的三种类型:第①②题是小数乘整数;第③⑤⑥题是小数乘小数,分别为一位小数乘一位小数、一位小数乘三位小数但转化为整数是三位数乘两位数、一位小数乘两位小数但转化为整数是两位数乘三位数;第④⑦⑧题是小数乘整十数。
本研究分别于2021年和2023年对两届学生进行了对照实验。结果显示,两届学生的实验结果基本一致。以2023年为例,对学校五年级240人进行了前测。其中,有42人全对或只是在进位上出错,表明他们已提前掌握了小数乘法。因此,在统计实验人数时,这42名学生排除在外(仅在统计数据时排除,实际教学时仍正常参与)。实际列入对照分析的学生人数共计198 人,其中实验班人数为95人,对照班人数为103人。
分析结果显示,小数加减法的正确率较高,达到了约92%。研究还发现,小数加减法的正确率与小数乘法的正确率之间并无显著相关性,即加减运算的技能并不能直接迁移到乘法运算中。然而,加减运算的经验却对乘法运算产生了普遍的负迁移。具体前测情况如表1所示。
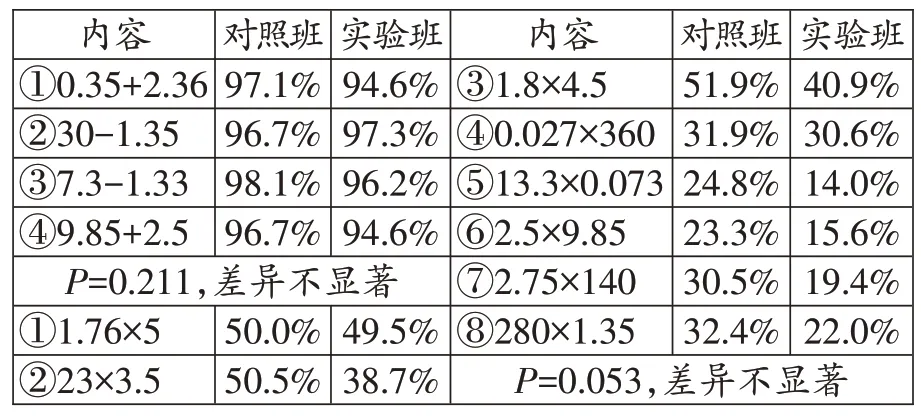
表1 前测正确率统计表
从上表可以看出,对照班在每一题上的正确率几乎都略高于实验班,但差异并不显著。在前测中,学生的主要错误来自小数点的干扰,从而造成对位混乱以及积的小数位数错误。由此可见,亟须探索一种有效的方法来使学生摆脱这一困境。
四、教学实验
(一)实验设计
鉴于将小数乘法整数化处理后,“小数乘整数”与“小数乘小数”的算法就达成了统一,因此将它们合并于同一课时进行教学。教学设计遵循浙教版教材五年级上册“小数乘法”的有关内容,具体分为五个环节:(1)情境引入。(2)让学生独立思考并交流7.8×2的竖式计算方法,通过面积模型理解算理。(3)延伸,尝试数学情境中0.55×2.6 的计算。(4)巩固练习。根据因数判断积的小数位数、直接由整数积得出小数乘法结果,以及列竖式计算2.5×0.08、2.5×1.36、0.036×3500 等。(5)课堂小结。在对比实验过程中,对照班与实验班的主要区别在于“列竖式”这一环节,即实验班在列竖式时将因数由小数改成整数,以减少小数点对计算的干扰。那么,这一细微改变将如何影响教学效果呢?
(二)实验结果
为便于对比分析,后测卷与前测卷的内容保持一致,具体结果如表2所示。
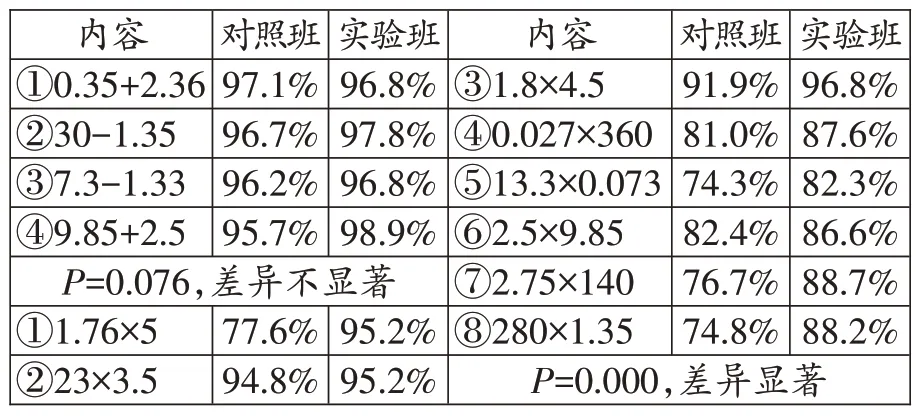
表2 后测正确率统计表
对于小数乘法计算,经过与前测数据的对比,发现实验班每一题计算的正确率都超越了对照班。实际上,从2021年的实验开始,就发现这样的竖式计算对学生帮助很大,效果明显,所以这次笔者将基础稍显薄弱的班级作为实验班。从后测数据来看,实验班的正确率还是全面超越对照班,并未对原有的小数加减法计算能力产生负面影响。更值得关注的是小数乘法中最容易出错的两种情况,经过测试验证,新方法在以下两个方面表现出的差异显著:(1)当两个因数相乘的结果的末尾为0时,如1.76×5(P=0.000),新方法显著提高了正确率;(2)当小数乘整十数,且因数本身含有0,乘积末尾也有0时,如2.75×140(P=0.004)、280×1.35(P=0.002),新方法同样展现出了明显的优势。
五、分析与讨论
从后测结果来看,实验班在计算正确率上显著超越了对照班。这一令人欣喜的进步在小数乘法的教学中具有特殊意义。这是因为小数乘法的竖式计算历来都被视为教学中的难点,尽管教师反复强调,学生也经过了反复的练习,但仍无法完全掌握,经常出现反复犯错的情况。
现在,笔者只是在本实验教学中作了一点小小的改进,就观察到了显著的效果。这种改进基于运算的一致性原理,将小数乘法整数化后转化为整数乘法进行计算。这种方式用横式对应算理、竖式对应算法,使得学生在处理竖式计算时,能够将其视为与整数乘法完全相同的计算方法。这一转变消除了数位对齐和末尾对齐两者之间差异对学生的干扰,从而显著提高了学生的计算正确率。进一步分析表明,在传统的算法中,竖式计算中因数带小数点对成人来说可能影响不大,但对于学生来说却是一个很大的挑战。这主要是因为学生的大脑皮层尚未发育完全,神经元连接的稳定性相对较弱,导致他们在处理类似问题时更依赖于原有的认知结构。所以,当对新的教学内容作微小的改动,以融入学生原有的认知结构时,他们会更容易掌握。
类似地,对于小数除法的易错点——除数是小数的除法问题,也可以从运算一致性的视角出发,将除数整数化来解决。例如:35.7÷0.17=3570÷17=210、3.57÷0.17=357÷17=21、0.357÷0.17=35.7÷17=2.1。这种方法实际上在多年前就已被提出,并在一些学校中得到了应用。在浙教版教材五年级上册中,小数除法的竖式计算就同时呈现了“画去小数点”和“整数化”两种方法,而学生在实际应用中更倾向于使用后者,认为这种方式更加清晰明了。
尽管小数除法竖式计算的整数化方法已经进入教材多年,并帮助无数学生提高了计算正确率,但小数乘法的竖式计算是否也可以作为算理算法相融的一种样例进入教材呢?提供多种选择对学生来说无疑是有益的,而且从运算一致性的视角来看,这种方法有助于学生从整体理解和掌握四则运算的算理。希望本文能引起更多教师的关注,并开始深度尝试这种教学方法,从而为学生带来更好的学习效果。
