在运动的视角下,联通“图形与几何”的结构
——以人教版教材“立体图形的体积和表面积”的教学为例
2024-05-06张伟明梁婷婷
□张伟明 梁婷婷
一、缘起
《义务教育数学课程标准(2022 年版)》对“图形与几何”领域进行了调整,将《义务教育数学课程标准(2011 年版)》中的“图形的认识”“图形的测量”“图形的运动”“图形的位置”四个主题,整合为“图形的认识与测量”“图形的位置与运动”两个主题。这一变化说明“认识”与“测量”、“位置”与“运动”在教学内容上紧密关联。比如,图形特征的刻画有助于测量方法的掌握,而测量方法的习得又有助于图形特征的理解。两者又可以通过图形运动的视角实现关联,即在图形的运动中认识图形特征,掌握测量方法,实现图形特征认识与图形运动之间的一致性,使各主题紧密结合。
那该领域的教学内容应如何展开深入思考与实施呢?对此,笔者参阅吴正宪老师、张秋爽老师关于“以运动视角刻画图形特征”和“以运动视角理解图形测量”的观点[1],结合人教版教材六年级下册“整理和复习”单元中的“立体图形的体积和表面积”这一内容进行实践。一方面,作为小学阶段“图形的认识与测量”领域的最后一课,“立体图形的体积和表面积”的教学需要对立体图形的体积和表面积进行系统梳理;另一方面,这一复习内容对学生整合所学的有关图形的零碎知识提出了更高要求(如图形的特征、图形之间的关联、计算公式的由来等)。
二、教学实践
(一)第一次图形运动:以图形特征为焦点,激活知识链
对图形特征的认知主要体现在对图形的抽象上。为此,学生需经历从实际物体抽象出几何图形的过程。以图形的运动为视角,可通过图形的动态演绎,使学生对图形特征的理解变得更为深刻。比如,三维直柱体也可通过二维平面图形垂直平移得到。由此,学生从运动变化中再次认识点、线、面等特征,以已有的知识点为基础,激活知识链。
在本内容的导入环节,教师先以课件的动态方式演示“点动成线、线动成面、面动成体”的过程,直观呈现图形的形成过程:一个点沿一个方向平移,运动后的轨迹是一条线(如线段)。一条线段沿同一个方向平移,运动后的轨迹能形成长方形、正方形、平行四边形;将这条线段绕着一个端点旋转一定角度,运动形成的轨迹是圆(或扇形)。将平面图形平移可形成长方体、正方体、圆柱,旋转可形成圆柱或圆锥(如图1)。这一图形运动过程再现了一维、二维和三维间的转化,为学生回顾图形的特征奠定基础。接着,教师提出核心问题:“看到V=Sh的计算公式,你想到了哪些图形的体积?你想怎么说明?”通过问题驱动,帮助学生回忆并整理出长方体、正方体、圆柱等立体图形都能用这一公式计算体积。具体来说,长方体的体积为abh,正方体的体积为a³,圆柱的体积为πr²h。其中,ab、a²、πr²为底面积,h(a)为图形的高。在运动视角下,学生能快速回忆起各种立体图形的特征,为形成知识结构奠定基础。

图1
(二)第二次图形运动:贯通图形测量,构建知识网
图形的长度、面积、体积计算公式的推导建立在测量基础上,比如:长方形的面积是以面积单位对“行”和“列”进行测量,从而归纳出长方形的面积公式;长方体的体积是以体积单位对“行”“列”和“层”进行测量,进而归纳出长方体的体积公式。教师应从运动的视角出发,帮助学生利用测量理解体积的计算公式,发展空间观念。
在本内容的展开环节,教师可以利用V=Sh的计算公式,求长方体、正方体、圆柱的体积,并引导学生思考:“你如何解释这些立体图形的体积都可以用V=Sh来计算?”以此引导学生回归体积推导的基本图形——长方体,并由此推理其他立体图形的体积,丰富学生对测量内涵的理解。
【教学片段1】
师:我们是如何推导长方体的体积公式的?
生:用1 立方厘米的小正方体进行摆放,一行摆a个,摆了b行,有这样的h层,长方体的体积就用abh来计算。
师:长方体的底面积a×b表示一层中每一行有a个小正方体,共有b行,即一层有几个体积单位;h是指有这样的h层。体积单位的个数可以用一层的个数×层数,即Sh来计算。那么,正方体的体积如何计算呢?
生:正方体的一层中,每一行a个小正方体,有a行,有这样的a层,同样可以用Sh来计算。
师:那么圆柱呢?
生:一层有πr²个小正方体,有h层。
师:这样能看出体积单位吗?
生:将圆柱平均分成16等分,拼成一个近似的长方体。这样,一层中每一行有πr个小正方体,共有r行,有h层。因此,圆柱的体积也可以用V=Sh来计算。
师:这个S和h究竟代表什么?
生:S就是一层有几个小正方体,h就是有几层。
师:有同学提到三棱柱也能用V=Sh计算体积。你知道三棱柱的形状吗?你想如何来说明?
生:三棱柱的底部是“一层三角形”,它有几层这样的三角形,体积可以用V=Sh来表示。
在运动视角下,引导学生理解S表示平面图形的面积,h表示平面图形平移的距离。当平面图形的面积不变时,运动的距离越长,直柱体的体积越大;反之,运动的距离越短,直柱体的体积越小。由此推导立体图形的体积=平面图形的面积×运动的距离。这使得学生体会到各类直柱体体积计算方法的一致性,认识到这些直柱体的体积都能用V=Sh来计算。
【教学片段2】
师:一层的高最小是不是1 厘米?如果将1 厘米继续缩减下去,你能想象此时的形状吗?
生:高为1毫米的一层。
师:这时用于度量的体积单位是什么?
生:1立方毫米。
师:高还能再小下去吗?
生:1微米、1纳米……
师:你能想象出这个图形的形状吗?
生:很薄很薄的一片。
师:那么S表示什么?h又表示什么呢?
生:S表示平面图形的面积,h表示平面图形平移的距离。
师:是的,因此立体图形的体积=平面图形的面积×运动的距离。我们将这种可以通过平面图形平移得到的立体图形称为直柱体。
教师从立体图形体积的计算过渡到表面积的整理。如沿圆柱的一条高剪开,可得到两个圆形的底面和一个长方形的侧面;对于长方体、正方体、三棱柱等图形,沿一条高剪开,也可得到两个底面和一个长方形的侧面。这些立体图形的侧面都是长方形,其面积均由底面周长C平移h这一距离得到(如图2),因此这些立体图形的侧面积也能用底面周长×运动距离来计算。教师通过板书(如图3)整理相关知识,让学生体会到在运动视角下,体积和表面积的计算方法更具有一般性和一致性。
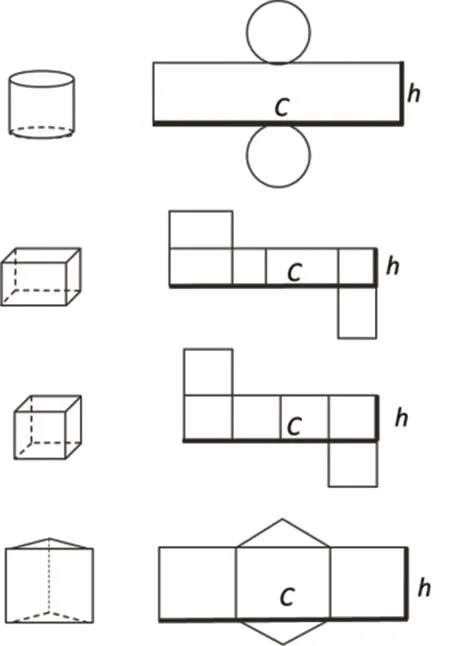
图2
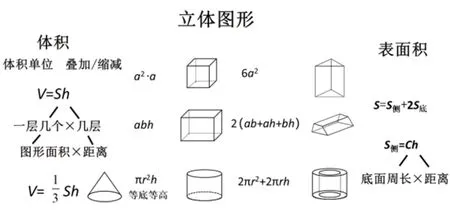
图3
(三)第三次图形运动:类化图形结构,实现知识迁移
图形的运动不仅是具体的学习内容,也是一种思维方式。通过图形的运动,学生可以深化对图形的认识与测量,这有利于他们用数学的眼光观察图形世界,体会图形在现实生活中的广泛应用,进而认识到数学的价值。
在本内容的练习环节,教师出示了9个封闭的立体图形(如图4),要求学生根据提供的数据找一找9个图形容积之间的关系。在之前的展开环节,学生已经探究出立体图形体积与平面图形及运动距离之间的关系。因此,学生能够迅速发现②号、④号、⑤号、⑨号立体图形的容积相等。这一过程促使学生理解在直柱体中,底面图形可以从原来的正方形、长方形、圆、三角形扩展到平行四边形、梯形、圆环,甚至任意的平面图形。
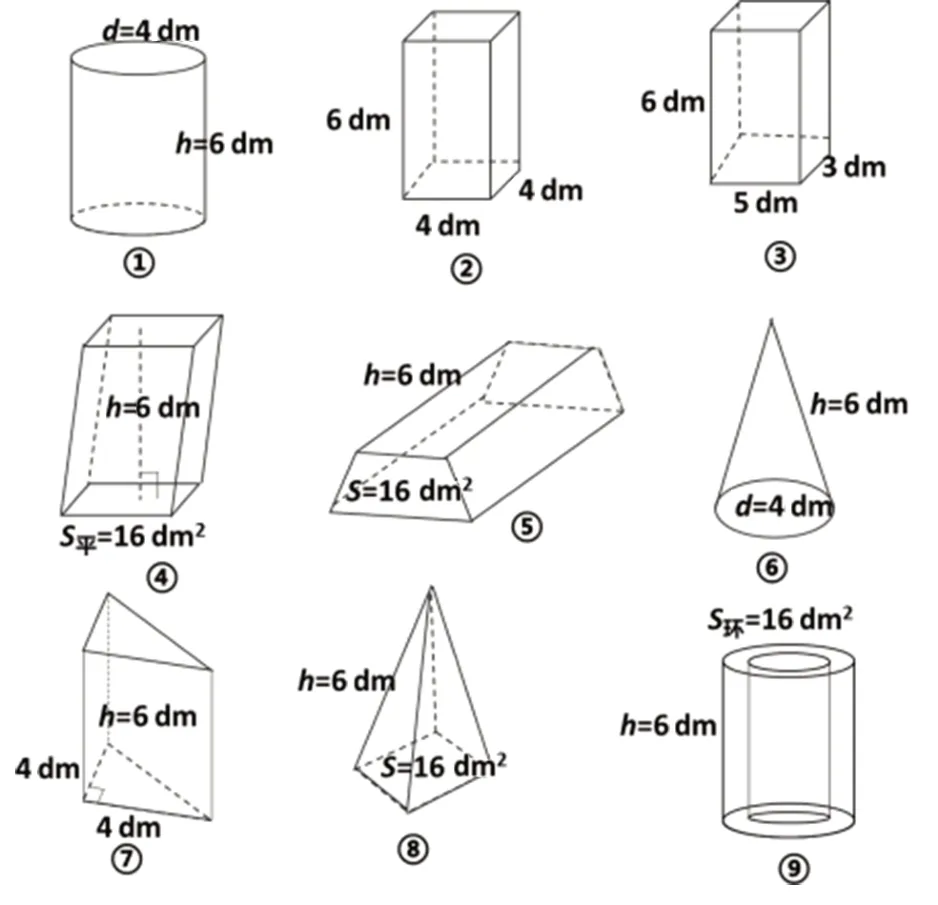
图4
【教学片段3】
师:大家说的平行四边形、梯形、圆环……都是平面图形的形状,那么平移的方向呢?
生:可以上下、左右平移。
生:还可以斜着平移。
师:是的,就是这里的④号棱柱。那你是怎么理解它的高的?
(根据学生的比画,将三本数学书叠在一起进行演示,让学生理解斜棱柱的高是面与面之间垂直线段的长度)
师:你还能发现其他关系吗?
生:②号图形的体积是⑦号图形体积的2 倍。⑦号图形的底面是直角三角形,两个完全一样的直角三角形可以拼成一个长方形。
(根据学生回答将两个三棱柱拼成长方体)
生:我知道了,平移距离相等,平面图形的面积就成为决定体积的关键要素。因此,平面图形面积推导中使用的倍拼法,同样可以用于推导立体图形的体积。
生:我还发现①号圆柱体的体积是⑥号圆锥体体积的3倍。
生:我觉得②号长方体与⑧号四棱锥的体积之间也存在3倍关系。
师:你们会如何验证这一猜想?
生:制作等底等高的长方体容器和四棱锥容器,将四棱锥容器倒满水,再倒入长方体容器中,重复这个过程,看看是否需要3次。
师:这是很好的想法!
在本内容的总结环节,教师带领学生梳理并回顾“正三角形—正方形—正五边形—正六边形—正十八边形”的形成过程。随着正多边形边数的增加,其形状无限趋近于圆形,直至完全变为圆形。教师提问:“这些正多边形可以通过垂直平移得到相应的直柱体,那么这些直柱体的体积应如何计算呢?”借助在运动变化中特征保持一致的图形,帮助学生得出“棱柱体积都可以用底面积×高计算”的结论。而圆锥的体积是与它等底等高圆柱体积的据此可引导学生推导出棱锥体积也应是与之等底等高棱柱体积的(如图5)。由此,学生解决问题的思维从静态地分析基本图形的组成,提升至基于关系分析图形特征和等积变化,实现了知识的关联和结构化。

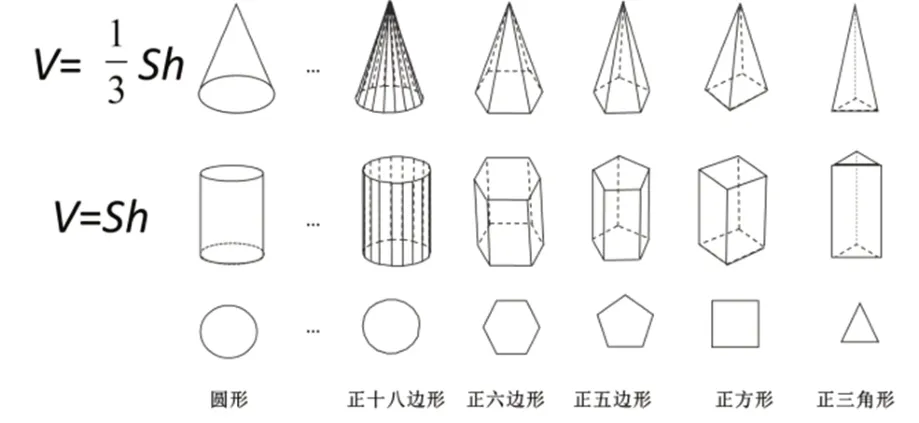
图5
总之,在运动视角下进行的“立体图形体积和表面积”的教学实践,在激发学生的讨论、互动及思维发展方面取得了令人满意的成果。通过三次图形的运动过程,将“立体图形体积和表面积”的复习融入知识链激活、知识网构建以及知识迁移应用的过程中,使学生对图形特征有了直观的认识,构建了合理的测量方法,并拓展了对类化图形结构的理解,从而推动了学生核心素养的发展。
