源于情境 类比抽象 应用深化
——以“分量+分量=总量”模型构建为例
2024-05-06盛国平盛勤杰
□盛国平 盛勤杰
数量关系不仅是解决问题的核心,也是培养学生核心素养的关键。《义务教育数学课程标准(2022年版)》强调让学生经历在具体情境中运用数量关系解决问题的过程,并明确提出“分量+分量=总量”这一数量关系,为数量关系的教学提供了清晰的方向。
然而,在课堂中存在教学零碎化和片面性的问题。部分教师过于侧重计算技能的培养,这在一定程度上削弱了学生构建数量关系的能力。如何有效进行数量关系的教学?对此,不少教师感到迷茫。本文以人教版教材三年级上册“三位数加三位数”的教学内容为例,探讨如何借助具体情境,引导学生自主探究,深入理解“分量+分量=总量”这一数量关系的形成过程,进而培养他们的自主探究能力与数量关系的构建能力。
一、利用现实情境,感知数量关系模型
教师通过实物或图片,为学生构建与生活息息相关的现实情境,引导学生在提取并分析信息的过程中,激活已有知识经验,形成新的认知冲突。同时,通过数形结合,帮助学生理解现实情境,切实感悟数量之间的模型关系。
(一)创设情境,提取信息
学生对数量关系的理解必须建立在具体的情境之上。通过对具体情境的感知,学生就能够从中提取并分析出与数量关系紧密相关的信息。
师:学校组织同学们到动物园参观。这些湿地野生动物你都了解吗?
教师用课件出示主题图(如图1)。

图1
师:湿地孕育了丰富多样的野生动物,下面是关于中国湿地部分动物重量的统计表(如表1),你从中获得了哪些数学信息?
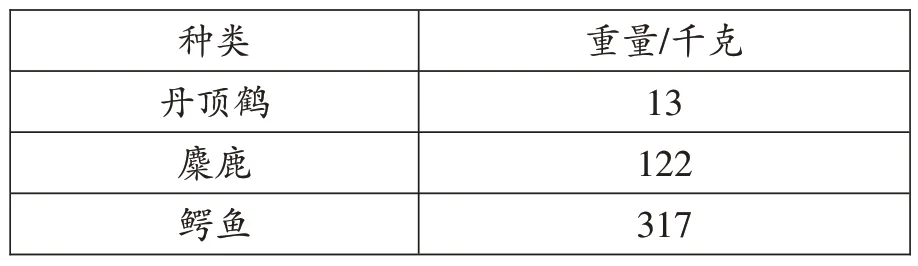
表1
生:湿地动物丹顶鹤重13 千克,麋鹿重122 千克,鳄鱼重317千克。
师:你们能据此提出与数学有关的问题吗?
生:丹顶鹤和麋鹿一共重多少千克?
生:麋鹿和鳄鱼一共重多少千克?
生:丹顶鹤和鳄鱼一共重多少千克?
生:麋鹿比丹顶鹤重多少千克?
将生活中的实例引入数学教学,可以拉近课堂与实际生活之间的距离,使学生更易于发现情境中的数学信息。学生通过对这些信息的搜集和分析,可以提升信息搜集与处理能力,进而发展数学素养和实践应用能力。
(二)找共同点,激活经验
学生已有知识经验是他们学习新知识的基础。为此,教师在教学中要善于找到新旧知识点之间的联系。
师:同学们刚刚提出了那么多数学问题,现在,我们先一起解决“麋鹿和鳄鱼一共重多少千克?”的问题。
师:这一题要求我们求麋鹿和鳄鱼一共重多少千克。大家回忆一下,我们什么时候学过与求“一共”相关的内容?
生:一、二年级时学过。
引导学生深入探索并发现和以往知识的共通点,可以有效激活学生的已有知识经验,使他们能够在学习新知识的过程中更好地形成知识体系,并加强知识之间的联系。
(三)借助线段,数形转化
为了使学生能够直观地感知模型,教师在教学中需要借助数形结合的方式,将抽象的数学模型与具体的图形相结合,从而帮助学生更好地理解模型的内涵。
学生选取信息并提出问题后,教师出示问题:麋鹿和鳄鱼一共重多少千克?
师:你们能用图式来表示这些信息和问题吗?
学生动手操作,画一画、摆一摆。
师:我们以前是用画小方块或者摆小木棒的方式来表示这类问题中的数量的,现在你们觉得还合适吗?
生:不合适,因为数太大了。
师:那该怎么办呢?
生:我们可以用线段来表示某一个数量。
学生用画线段图的方式表示题目中的数量关系(如图2)。
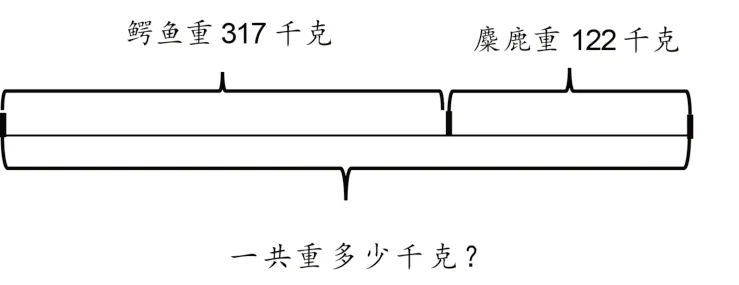
图2
师:你能说一说这幅线段图表示什么意思吗?
生:我先画一条线段表示鳄鱼重317 千克,再在它的后面画一条线段表示麋鹿重122千克,下面这个问句就表示这两种动物一共重多少千克。
画图的实质是借助图形表征帮助学生把抽象问题具体化、直观化,从而使学生能通过直观感知与数学抽象的深度融合来理解题意,并分析数量关系,寻找到解决问题的突破口,实现知识的有效迁移。
二、利用迁移类比,提炼数量关系模型
为使学生更好地掌握数量关系,教师需要引导他们回顾已有的相关知识,并运用类比推理的方式,逐步从已知的关系中抽象概括出具有普遍意义的数学模型。
(一)运用语言描述,初步抽象规律
用自然、生动的语言来描述规律,是学生学习和认识规律的初步阶段。通过语言描述,学生能够初步感知规律的存在和形式,从而建立起对规律的基本认识。
师(出示图2):鳄鱼的重量和麋鹿的重量合并起来就是一共重多少千克。你能模仿老师的方法说一说吗?
小组合作后交流。
生:丹顶鹤的重量和鳄鱼的重量合并起来就是一共重多少千克。
生:丹顶鹤的重量和麋鹿的重量合并起来就是一共重多少千克。
教师引导学生联系运算的意义,在充分理解问题的基础上,用自己的语言表达量与量之间的关系。如学生可以使用“……和……合并起来就是……”“……和……就可以求出……”等表达方式。这种语言描述方式不仅能够帮助学生将观察到的现象进行系统化整理,而且为他们学习如何将具体现象抽象为数学模型打下了坚实的基础。通过这种方式,学生不仅能够提高数学运算能力,还能够提升逻辑思维和抽象思维能力,为未来的学习奠定良好的基础。
(二)积累学习材料,进行类比分析
学生在学习中对规律的发现是一个渐进的、积累性的过程。只有不断积累学习材料,他们对规律的认识才能逐渐变得清晰和深入。
教师出示学习单(如表2)。

表2
要求:先填一填题目中已知什么、求什么,再列式解答。
教师利用列表的方式呈现三个题目的解决过程。通过讨论、比较,学生发现这三道题目的相似之处,即它们都是将描述两种动物的重量的数进行合并。通过对学习材料的积累与整理,学生获得了丰富的学习经验,并经过类比推理,发现这些题目本质上具有一致性,即都符合“分量+分量=总量”这一数量关系。
(三)通过已有经验,得出基本模型
在日常生活中,许多学生都有过与天平接触的生活经验。作为一种称重工具,天平的显性功能在于衡量物体的重量。同时,它还是数学中“表示两边相等”的基本模型。
教师出示天平图(如图3)。

图3
师:这幅图中的物品是天平,它有什么特点?
生:左右两边平衡,就表示左右两边相等。
师:现在,如果老师让你将之前提到的动物放到天平上,你会怎么放?
(小组讨论)
师:想象这里有一个超级大的天平,左边托盘上站着重317 千克的鳄鱼和重122 千克的麋鹿,右边托盘上放多重的物体,天平才会平衡呢?
生:放重量为439千克的物体,即317+122=439(千克)。
师:如果左边托盘上换成重317千克的鳄鱼和重13千克的丹顶鹤呢?
生:右边托盘上放重量为330 千克的物体,天平会再次平衡,即317+13=330(千克)。
师:那如果左边托盘上换成丹顶鹤和麋鹿呢?
生:右边托盘上放重量为135 千克的物体,天平会再次平衡,即13+122=135(千克)。
师:天平右边的数和左边的数有什么关系?
生:右边是总量,左边的两个量相加就是右边的量。
师:如果左边的量称为分量,那右边的量可以称作什么呢?
生:总量。
师:我们可以把它们的关系概括为:分量+分量=总量。
天平是数学上表示两个数量关系的直观模型,能够为学生理解相等数量关系提供帮助。
三、开展拓展训练,应用数量关系模型
开展拓展训练是促进学生内化数量关系模型的关键环节。通过多样化的实践应用,学生可以进一步实现对数量关系模型的理解,并逐渐将其内化为自己的思维方式。
(一)拓展运用,巩固模型
●题目:菜场运来白菜112筐,青菜32筐,_________?
师:你能把题目补充完整吗?
生:一共运来多少筐蔬菜?
师:你能用“分量+分量=总量”来分析一下吗?
生:分量是白菜的筐数和青菜的筐数,总量是蔬菜的总筐数,因此白菜的筐数+青菜的筐数=蔬菜的总筐数。
生:112+32=144(筐)。
加法模型“分量+分量=总量”是数学中一种基本且重要的概念,它描述了一个整体由两个或多个部分合并组成的情况。教学中,教师要引导学生思考、讨论分量和总量各自所代表的含义,帮助学生将加法模型抽象化,从而加深对“分量+分量=总量”模型的理解和应用。
(二)运用变式,内化模型
●题目:妈妈把32个苹果放在两个盘子里,一个盘子里放了8个苹果,____?
师:你们能补充一个问题吗?
生:另一个盘子里有几个苹果?
师:你们能找一下这一题的分量和总量吗?
生:32个苹果是总量,8个苹果是分量,要求的也是分量。所以这一题应该是用“总量-分量=分量”解决。
生:32-8=24(个)。
加法模型的变式可以表达为“总量-分量=分量”。这是对“分量+分量=总量”这一数量关系模型的逆向运用,可以实现数量关系的结构化迁移,从而加深学生对加法模型概念的理解。这样的学习有助于学生形成网状知识结构,丰富学生的数学基本活动经验,使学生逐渐形成数学思想方法。
●题目:小红今年18岁,比小明大了2岁,________?
师:请补充问题。
生:小明多少岁?
师:你能用今天学习的数量关系对题目进行具体分析吗?
生:小红的年龄是总量,小明的年龄和相差的2岁都可以看成分量。
生:小明的年龄+2岁=小红的年龄。
在理解数量关系的过程中,学生应认识到合并关系可以进一步拓展为增加关系。除了掌握这些基本的数量关系,学生还需深入理解“又来了”“多了”“增加了”“走掉了”“用去了”等词语的内涵。教师要通过这样的教学,引导学生掌握分析问题的方法,提高他们的审题能力和分析能力,从而提升他们解决问题的能力。
(三)流程分析,深化模型
分析法和综合法是两种常用的思维方法,在解决问题中发挥着重要作用。同时,它们在深化模型理解方面也具有重要意义,能够帮助学生分析数量关系,提升分析能力。
●题目:宏光小学三年级有男生186 人,女生174 人,已经体检的有328 人,没有体检的有多少人?
综合法:从条件入手,找出中间问题,再解决所求问题(如图4)。
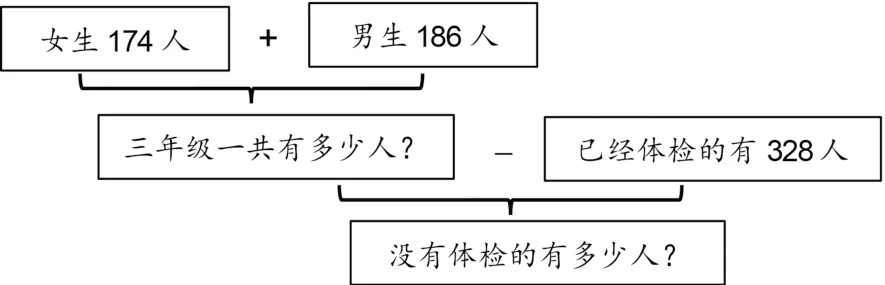
图4
根据男生186人和女生174人可以求出三年级一共有360 人。然后用360 人减去已经体检的328人,就可以求出没有体检的有32人。
分析法:从问题入手,寻求解决问题的条件,逐渐向已知条件靠拢,最后利用已知条件解决问题(如图5)。
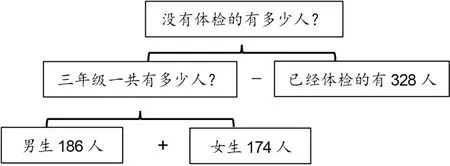
图5
要求三年级没有体检的有多少人,必须要知道三年级一共有多少人,再减去已经体检的人数。因为已经体检了328人是已知的,而三年级的总人数未知,所以要求三年级的总人数必须要知道三年级男生和女生各自的人数。
总之,通过自主建构加法意义的数量关系模型,即分量+分量=总量,学生能够更好地理解并掌握这一数量关系,这将为他们今后构建其他数量关系模型打下坚实的基础。
