大概念统领下的初中数学大单元作业设计研究*——以“一线三等角”大单元为例

魏相清|山东省广饶县教育科学研究中心

隆菲菲|山东省广饶县稻庄镇实验中学

作业是实现“教—学—评”一致性的重要载体，面对“双减”背景下“全面压减作业总量和时长，减轻学生过重作业负担”的要求，作业设计需要能够实现让学生“做少学多”的目的.以大概念为统领的大单元作业设计，能打破不同年级、不同册次的纵向联系和同一单元间的横向联系，引导学生进行“全景式”学习［1］，从而使作业走向“轻负高质”.下面，笔者以“一线三等角”大单元为例，具体探讨大概念统领下的大单元作业设计研究.

一、大概念的提取

大概念是一种核心概念，是一种教师希望学生记忆、理解并在忘记其非本质信息或周边信息之后，仍能应用的陈述性知识［2］.大概念是学科的核心内容，具有中心性.大概念是忘记非本质信息或周边信息后仍能保留下来的记忆，具有持久性.大概念是解决一个、多个乃至多类问题的通用策略，具有迁移性.

自变量与因变量的关系决定了函数模型，关系发生变化，函数模型就会相应产生变化.初中阶段主要学习一次函数、二次函数、反比例函数等，这些内容在研究对象的提出、描点画图、性质的研究等方面，都按照“定义→图象与性质→应用”的思路呈现，具有相通性和迁移性.

全等三角形与勾股定理属于图形与几何领域的“图形的性质”部分；相似三角形属于图形与几何领域的“图形的变化”部分.全等三角形与相似三角形在学习中都可按照“概念→性质→判定”的教学流程展开，具有一致性.同时，全等三角形还是研究勾股定理不可或缺的工具.

基于此，笔者提取“模型思想”为大概念，将分散在不同章节的勾股定理、全等三角形、相似三角形、函数等内容整合在一起，以此为学生构建前后一致、逻辑连贯的知识体系.

二、大单元的构建

“一线三等角”是一个常见的相似模型，指的是有三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角.该模型是初中阶段重要的几何模型之一，是中考考查的重点、热点问题.在有些试题中，这一模型会直接呈现，解题难度在中等以下，学生得分率较高；在另外一些试题中，学生需结合条件，构造出“一线三等角”模型，解题难度中等偏上，耗时多且得分低.笔者通过梳理“一线三等角”模型与相关知识的契合点，发现该模型源于勾股定理，基于全等三角形，兴于函数，终于相似三角形，然后基于此将基础性课时作业分为4 部分.大概念统领下的“一线三等角”大单元构建如图1所示.

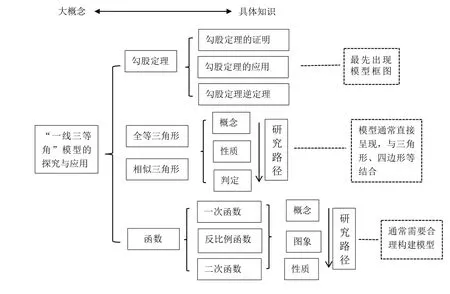
图1 大概念统领下的“一线三等角”大单元构建

三、大概念统领下的大单元作业设计

大概念统领下的大单元作业，指以一个大概念来组织目标、情境、知识点等课程要素，形成的需要相对较长时间和较多课时才能完成的、进阶性强的、相对完整的学习活动［3］.大概念统领下的大单元作业设计，则是以大概念为依托，整合多课时内容，对大单元作业目标进行一体化设计，对大单元作业内容及形式进行多样化设计，对大单元作业评价进行多元化设计.

（一）依托大概念构建一体化的大单元作业目标

课程层面，《义务教育数学课程标准（2022年版）》将抽象能力、几何直观、推理能力、模型观念等作为初中阶段的主要核心素养，这为大概念统领下的大单元作业目标设计明晰了方向.单元层面，笔者整体提取“一线三等角”模型这一核心概念，引导学生理解核心概念.课时层面，笔者在每一课时分设学习目标，引导学生应用模型逐步攻克基本问题.“一线三等角”大单元作业目标设计如表1所示.

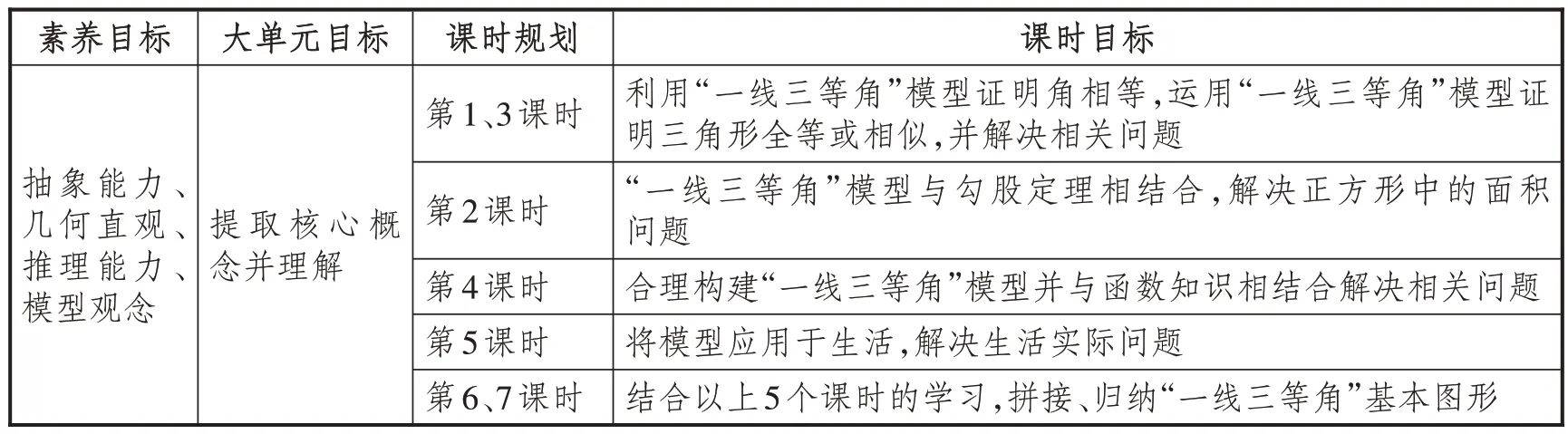
表1 “一线三等角”大单元作业目标设计

（二）围绕大概念整合多样化的大单元作业内容及形式

大单元作业有别于单一、静态的传统作业，集多元、动态于一体，既有基础性作业，又融合主题实践性作业.因此，笔者将“一线三等角”大单元作业分为7课时，其中前4课时为基础性作业，后3课时为主题实践性作业，具体如表2所示.

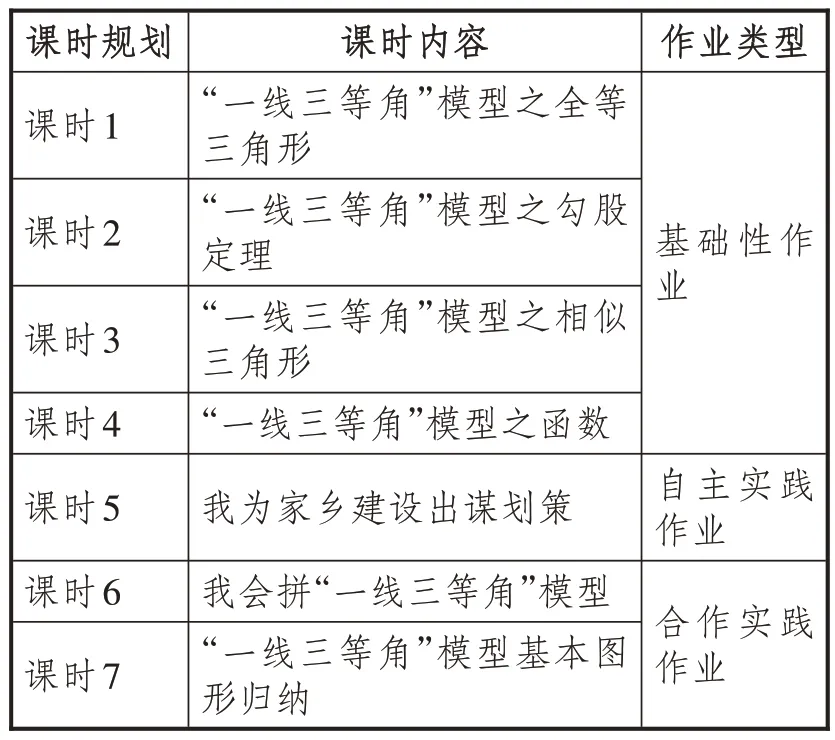
表2 “一线三等角”大单元作业规划

1.同一情境下的课时互通

大单元作业设计强化知识与情境之间的联系以及实现情境之间的互通，借助多重情境的互动帮助学生进行知识、技能和情感态度价值观的迁移与运用，形成多元思考［4］.下面是大情境下的序列化问题设计.

问题1：（第1 课时第1 题）如图2，将长方形纸片ABCD沿EH折叠，点D落在AB的点G处，点C落在C′处，∠GEF＝∠GFE.求证：AB＝AE+BF.

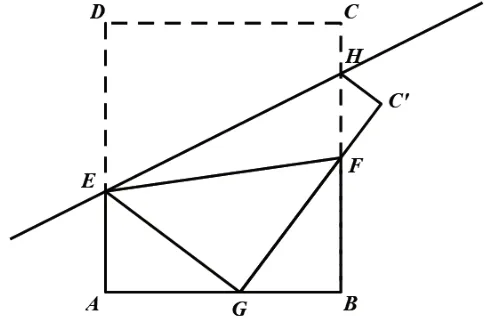
图2

问题2：（第2课时第1题）如图3，将长方形纸片ABCD沿EH折叠，点D落在AB的点G处，点C落在C′处，利用如图所示图形验证勾股定理，其中，△AEG和△BFG是以a、b为直角边，c为斜边的两个全等直角三角形.你能解释其中的道理吗？

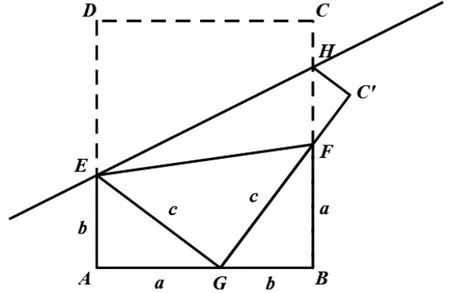
图3

提示：（1）试判断△EFG的形状：_____.（2）直角梯形ABFE的面积为________，也可表示为_______.（3）对比以上两种表示方法，可得出_______，整理得_______.

设计意图：两课时的第1题都围绕长方形的折叠问题展开，同一情境下，一站式探讨“一线三等角”模型在全等三角形、勾股定理和相似三角形中的存在性问题，以及在学生学习过程中出现的问题.

2.同一题目下的课时呼应

大单元作业设计强调教师为学生理解而教，高站位、高角度审视大单元作业内容，借助同一题目的呼应帮助学生体会变与不变的巧妙结合，对大概念建立深度理解.

问题3：（第1 课时第4 题）如图4，已知AC＝AB，∠D＝∠BAC＝∠E，在下面三个图形中任选其一，自主设计问题，并互问互答.

图4

问题4：（第3 课时第3 题）如图5，已知AC＞AB，∠D＝∠BAC＝∠E，在下面三个图形中任选其一，自主设计问题，并互问互答.

图5

设计意图：以上两道题目的区别在于条件一个是AC＝AB，一个是AC＞AB，引出的是全等三角形与相似三角形.两道题目分属于不同的课时，却又前后呼应，能体现大单元作业的情境互通.两道题目都属于开放性题目，难度较大，均放在该课时作业的末尾，需要有前面知识的铺垫，学生方可开拓思路，形成多元思考.

3.同一问题下的深度学习

以同一问题为基点，设计变式进行教学，可引发学生对问题产生新的思考与理解，促进深度学习.

问题5：（第2课时第3题）如图6，在直线l上依次摆放着三个正方形.已知斜放置的一个正方形的面积是3，正放置的两个正方形的面积依次是S1、S2，则S1+S2＝_______.

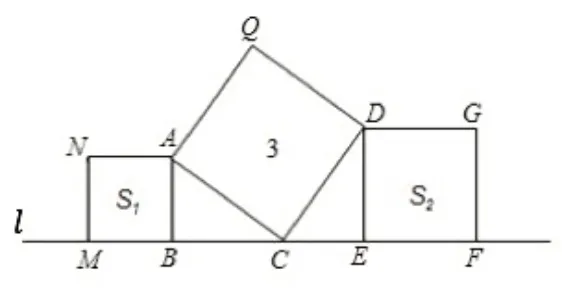
图6

问题6：（第2课时第4题）如图7，在直线l上依次摆放着七个正方形.已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4，则S1+S4＝_______.

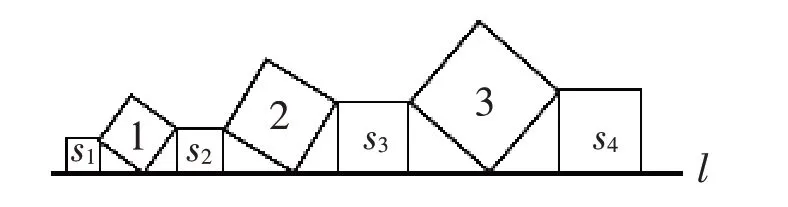
图7

设计意图：问题5是对“一线三等角”模型的直接考查，要求学生能够证明全等，进而利用勾股定理，得到三个正方形的面积关系.问题6 是在勾股定理与“一线三等角”模型结合的基础上，又引入等式加减，变换得出两个正方形的面积和.如此，以变式促学，并层层深入，可不断引导学生产生新的思考，促进学生深度学习.

4.同一主题下的实践研究

主题实践作业是连接数学与生活的一座桥梁，可以重塑学生的学习兴趣，提高学生的综合素养.

问题7：（第5 课时自主实践作业）孙子文化园（园区景点示意图略）位于山东省东营市广饶县，其人文景观包括凝聚了孙子文化的兵圣宫、兵法十三桥、兵圣天下、春秋古镇、尚武遗风（兵器展示区）、攻城演绎（攻城演绎区）.如图8，假设九变桥至兵势桥部分原计划按OA-AB的方向施工，由于AB方向地势等原因，修建须绕开此区域.经实地勘测，若将AB段绕点A顺时针或逆时针方向旋转45°至AC或AD方向，则可以绕开此区域.已知OA长为1 千米，以点O为原点，OA所在直线为x轴，1千米为单位长度，建立平面直角坐标系，且射线AB与直线y＝-2x平行，请帮助施工队计算出AC和AD所在直线的解析式.

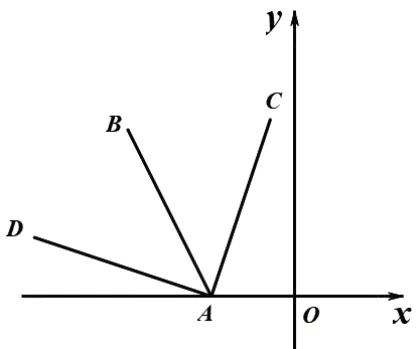
图8

设计意图：此题以孙子文化园为背景，在增强学生家乡自豪感的同时，使其体会数学来源于生活，又将服务于生活.从生活中列举实例，转化为数学问题，并采用“一线三等角”模型解决问题，引导学生学会用数学的眼光观察现实世界、用数学的思维思考现实世界、用数学的语言表达现实世界.

（三）基于大概念设置多元化的大单元作业评价

传统作业往往重结果轻过程，评价标准绝对化、单一化；而大单元作业强调学生核心素养的培育、综合能力的提升，因此过程更重要.对“一线三等角”大单元作业，笔者采用“我的得分表”等量表对学生进行评价，将自评、他评、师评等多元评价加以整合.评价的结果为课后复习延伸作业的布置服务，并以此设置分层作业.

1.基础性作业评价量表

笔者设计了“我的得分表”与“课堂总结与分层作业评价表”.“我的得分表”总分为15分，自评得分、他评得分、师评得分栏填写A、B、C、D 等级.得分栏根据等级A、B、C、D 折合得分.等级A 对应5 分，等级B 对应4 分，等级C 对应3 分，等级D 对应2 分，修改后答案仍存在错误得0 分.12～15 分为优秀；8～11 分为合格；8 分以下为有待提高.以第1 课时为例，笔者对课堂总结与分层作业设计的评价表如表3所示.

表3 课堂总结与分层作业评价表（第1课时）

设计意图：在每课时“课堂练习作业”完成后，都会对应一个“我的得分表”，师评得分可由教师随堂批改填写，自评得分由学生在课上实时填写，他评得分由学生所在小组在课堂作业讲解完成后根据修改情况填写，最后由组长计算出总分.总分多少与等级是相对应的，学生根据总分，得出“我的等级”，参照等级完成分层作业，以期实现“减量增效”.“学后反思”环节则能帮助学生发现问题，总结经验，明晰方向，实现更好的发展.

2.实践性作业评价标准

笔者结合实际作业要求，引导学生以6人为一组，在限定的时间内开展合作探究.下面以第7 课时的实践性作业评价标准设计为例说明.

［教师评价］主要评价学生的参与程度以及所表达出来的思维方式，与同学合作交流的意识与能力等，分为A、B、C、D四个等级，分别对应优秀、良好、一般、合格.

A 级：模型准确、条理清晰、讲解准确、过程完整，至少5人参与发言.

B 级：模型准确、讲解明了、过程完整，至少4人参与发言.

C 级：模型准确、讲解不明、过程一般，至少3人参与发言.

D 级：准备不全、讲解不明、过程一般，至少2人参与发言.

［学生自评与他评］主要评价小组归纳总结得出的基本图形的合理性，分为A、B两个等级，分别对应优秀、良好.

A级：拼接正确，讲解明了，过程完整.

B级：准备不全，讲解不明，过程一般.

四、几点思考

笔者将大概念与大单元作业设计的要素相结合，探索出大概念统领下的大单元作业设计的基本路径主要包括三个环节、三个重点.大概念提取是第一环节，大单元构建是第二环节，大单元作业设计是第三环节，而在第三环节中，作业目标、作业内容、作业评价的设计是重点.

（一）大概念提取是关键

在大单元作业设计中，大概念是灵魂，并在知识体系中居于上位，可以统摄一切下位知识.数学学科的大概念既可以是一个核心概念，也可以是某单元要研究的核心问题，还可以是主要的模型、思想、方法等.因此，教师可从以下三方面提取大概念：（1）基于课程标准的解读，自上而下探寻核心概念，提取单元大概念；（2）指向核心问题的解决、核心任务的达成，融合生成大概念；（3）基于迁移性较强的普适的模型、思想或方法提取大概念.大概念的提取与确定是大单元作业设计与实施的关键.

（二）大单元构建是基础

确定大概念后，下一步需结合内容重构大单元，这是大单元作业设计的基础.教师在构建大单元作业中需不断回溯单元设计的初衷，追问每道题目设计的意义，紧扣大概念，防止作业设计成为单纯的习题罗列.构建大单元可将看似不相关的知识通过大概念联结起来，帮助教师探寻课时之间的起承转合，厘清课时之间的内在联系.由此，教师再结合学情，即可设计出能引导学生更好发展的作业.

（三）大单元作业设计是核心

大单元作业设计是落实学科核心素养的重要手段，在设计作业时，教师应重点处理好作业目标、作业内容、作业评价的设计.作业目标是大单元作业设计的起点，也是检验作业设计成功与否的重要依据；作业内容是大单元作业设计的关键，是实现减量提质的有效手段；作业评价是连接作业目标与作业内容的桥梁.

1.关于大单元作业目标

大单元作业目标应立足核心素养，逐级向下细化目标，即由素养目标到单元目标再到课时目标，使各级目标相互渗透、融通，形成体系.在设计作业目标时，教师要兼顾学情，考虑学生原有的知识基础、活动经验、情感态度等，以及作业目标的可测性.

2.关于大单元作业内容

围绕大概念设计大单元作业内容，要体现大单元的整体性与连续性.例如，同一情境下的一站式探讨、同一题目下的课时呼应可实现前后课时的互联互通，同一问题下的深度学习、同一主题下的再探究可促进学生多元思考、提升学生的综合能力.

作业内容分为课堂练习作业与课后复习延伸作业两部分，二者相辅相成，让学生在连续出现的、进阶性强的练习中稳步提升.

3.关于大单元作业评价

作业评价应围绕作业目标展开.鉴于作业目标的可测性，基础性作业可采用量表形式，并在量表中融合自评、他评、师评等多元评价.作业评价也应成为作业再设计的重要依据.只有实现“计划—设计—实施—反馈—再设计”的作业设计闭环，教师才能在不断的优化中，设计出适合学生的高质量作业.实践性作业分等级，教师可鼓励学生积极参与，以实现大概念与生活的联通.

综上，大概念为大单元作业的设计提供了新思路.依托大概念构建一体化作业目标，围绕作业目标丰富作业内容与形式，创设同一情境下的课时互通、同一题目下的课时呼应、同一问题下的深度学习、同一主题下的实践研究，引导学生参与课堂，与教师共同探究，是实现深度理解与学习的重要方式.在此过程中，教师要合理使用师评、自评、他评等多元评价，提升学生的学习动力，发展学生的核心素养.