基于改进的Apriori 算法在高校成绩分析中的研究

张 梁，杨立波，张小勇，史俊冰

（太原学院智能感知与多维信息处理实验室 山西 太原 030032）

0 引言

高校学生成绩是高校实施素质教育的直接反映，各高校每年都存在学生对本专业内容掌握不扎实、对不同课程之间的联系不清晰导致的挂科等现象，对历史成绩数据进行成绩挖掘和分析有助于对学生的学习情况进行全面评估和管理，学生也可以从中得到学习经验，更好地规划学业［1］。成绩挖掘体现在海量成绩中“淘得真金”的过程，是指通过对每项有效成绩进行分析筛选，对成绩中隐含的、先前未知并存在价值信息的研究过程。

随着学生数量的增加和学科关联性的提升，考试成绩呈现出庞大而复杂的特征，而关联规则中的Apriori 算法处理大训练集时，通过高效的候选集生成和剪枝策略，能够快速挖掘出频繁项集和关联规则，众多学者将Apriori算法成功运用于学生成绩分析，并取得了显著的成果。付翠贞［2］提出差分隐私保护的Apriori 算法，在支持度－置信度体系下又引入提升度对关联规则进行挖掘，选取学生成绩数据集进行了有效验证并且评价了算法应用的有效性。廖宣植［3］利用WEKA 平台内置的Apriori 算法对临床专业课程进行了成绩挖掘，研究结果表明了医学、微生物学等专业课程之间存在关联性，并对研究结果进行了分析，给出了成绩预测模型。吴小东等［4］利用Apriori 算法对高校计算机专业学生的课程成绩进行了针对性分析，关注“不及格”和“优秀”成绩的关联规则，通过挖掘强规则，揭示了不同课程成绩之间的相互影响关系。然而上述研究样本空间涵盖的学生维度少，生成的关联规则可能无法捕捉成绩中各个项或维度之间的完整复杂关系，在此情况下关联规则可能偏向于某些模式，从而导致有偏差的推荐，并且在频度－可信度评价下将产生大量关联规则，其中冗余规则对实际分析帮助不大反而增加处理和分析的负担。

鉴于此，本文对某应用型高校智能系2017 级—2020级学生进行考试成绩分析，通过引入兴趣度和提升度的Apriori 算法对学生成绩进行关联规则分析，挖掘每一届学生在学习相同专业课程时取得的学习成果，旨在揭示潜在的关联规则，从而积极影响学生在学习专业课程方面的表现。

1 基于兴趣度和提升度规则关联算法模型

Apriori 算法基于先验知识原理，应用于大规模成绩样本中发现频繁项集和关联规则。经典的支持度－置信度框架是传统关联规则挖掘算法的核心，用于衡量关联规则的频繁程度和准确性。但它存在一定的缺陷，忽略了规则分布情况和多层次关联，在样本关联规则挖掘中，一些规则可能在成绩集中分布广泛但分析价值低，而其他规则虽不频繁，但在特定子集中体现出事务属性关联模式［5］。为了规避传统模式下缺陷，本文采用增添兴趣度、提升度和改进筛选标准等方法提升关联规则的质量。

1.1 增添兴趣度和提升度的关联规则机理

考试成绩样本中各学生一组成绩称为一个事物，每门课程成绩称为一个项。令I＝｛i1，i2，…，id｝ 是成绩样本中所有项的集合，而T＝｛t1，t2，…，tN｝ 是所有成绩样本中事务的组合，若A和B为I中的两个项集，同时满足，则A→B构成一个关联规则，所有关联规则组成成绩事务库D，其中事务集T同时支持A和B的事务数在成绩事务库D中的占比为Sup（A→B），形式化定义为式（1）；置信度则为同时存在A和B两个项集的事务数与只包含A项集事务数之比，形式化定义为式（2）。若Apriori 算法中满足Sup（A→B）≥Supmin 的规则项同时满足Conf（A→B）≥Confmin 要求，此规则即为强关联规则。

经典关联规则算法中支持度－置信度框架是存在缺陷的［6］，通过专业课模电和高频电子线路分析可以看出置信度高并不一定代表关联规则有分析价值。表1 中Sup（模电优秀→高频优秀）为14%，Conf（模电优秀→高频优秀）为70%，意味着模电成绩优秀的学生中有70%的可能性在高频中也表现出色，但整体高频课程中表现优秀的学生在总人数中占比为80%，意味着模电成绩优秀的学生在高频电子课程中表现出色的可能性虽然较高（70%的置信度），但整体而言，更多的学生在高频课程中表现出色，这与关联规则的置信度不一致。

表1 模拟电子技术和高频电子线路成绩样本

提升度和兴趣度的引入避免了类似上述矛盾的出现，提高了衡量关联规则的重要性和相关性指标。兴趣度对成绩样本中规则的前提和结果是否存在非随机关联进行了判断，Interest（A→B） ≥1 表示规则前提和结果存在正向关联，即规则中事务A对事务B有积极影响，形式化定义如式（3）。衡量关联规则的结果对前提的影响取决于提升度范围，提升度大于1 表示关联规则的出现提升了结果出现的概率，等于1 则二者无关，定义为式（4）。

1.2 关联算法流程

关联算法是在成绩事务库D中挖掘符合相关最小阈值设定的关联规则，整体算法流程由3 部分组成：

（1）迭代生成候选集。从频繁（k －1）－项集（记为（Lk －1）－）中获取每个项集的最后一项，然后将这些项排序。遍历频繁（k－1）－项集并逐个连接，生成候选k－项集的候选项［7］。Apriori 算法利用先验性质减少计算量，即对于生成的候选k －项集，它的所有子集都必须是频繁（k －1）－项集。算法对每个候选k －项集，遍历其所有（k －1） 项子集，不满足最小支持度阈值的要求则剪枝去除［8］。

（2）寻找频繁项集。针对每个候选k －项集，扫描整个成绩集，计算候选集在成绩集中的支持度，将满足最小支持度阈值的候选k －项集作为频繁k －项集，记为Lk。这些项集用于下一轮迭代直至算法结束。

（3）关联规则输出。对于每个频繁项集Lk，生成其所有可能的非空子集，作为关联规则的前项。对于每个规则的前项，依据规则的兴趣度、置信度等最小阈值设定筛选出满足要求的关联规则并输出。

2 Apriori 算法对成绩挖掘

采集完某应用型高校智能系2017 级—2020 级成绩数据后，运用Apriori 算法进行成绩挖掘。将考试成绩数据整合后获得328 名学生八门课程成绩共2 624 条成绩，每条包括学生姓名、学号、课程名称、课程编号、学分、成绩等14 项成绩属性，学生原始考试成绩如表2 所示。

表2 学生原始考试成绩

2.1 成绩预处理

（1）成绩清洗。成绩挖掘中并不关注学生姓名、学号等冗余信息，故在成绩预处理阶段将无用属性项删除，对原始成绩进行成绩降维操作，从而突出主要分析对象并降低计算和处理的复杂度。

（2）成绩离散化。降维后的成绩样本仍保留着连续的成绩值，而这些连续值可能呈现多样性和不均衡性等分布特点。为了加快挖掘的收敛速度，须对样本进行成绩离散化。通过离散化可以增强成绩数据的鲁棒性和降低过拟合风险，离散化后将成绩赋予类别标签，使得异常值在其类别中具有更高相似性，降低了模型受异常值影响产生过拟合的风险，在一定程度上平衡了成绩的不稳定性，离散化后成绩样本提高了关联算法进行规则挖掘的效率和规则的适用性。

鉴于上述分析结果，将各科目成绩样本离散化为5 个成绩等级依次为A、B、C、D、E，A 为最优，E 为差，离散结果如表3 所示。

表3 离散化成绩样本

2.2 成绩挖掘过程

挖掘过程［9］首先将成绩降维和离散化作为挖掘的预处理阶段，旨在消除成绩样本中异常值的影响［10－11］，从而形成更具代表性的样本集，其次应用改进的Apriori 算法对样本集挖掘其中蕴含的关联规则，通过设置观测阈值，可以筛选出具有显著意义的强规则，此类强规则反映了各科目间的关联关系，最终通过对符合阈值的强规则进行综合分析，得出各科目间相互影响的关系。

为了评估改进后的Apriori 算法在样本成绩中挖掘关联规则的效率，将对比传统的Apriori 算法与经过改进版本的挖掘效率，有助于在成绩事务库中进行关联规则分析时运行效率更高的算法［12］。将成绩事务库的2624 条成绩规整后对关联规则挖掘算法性能进行比较，设置不同参数下对比两种算法在置信度和支持度上的关联规则数量，结果如表4、表5 所示。

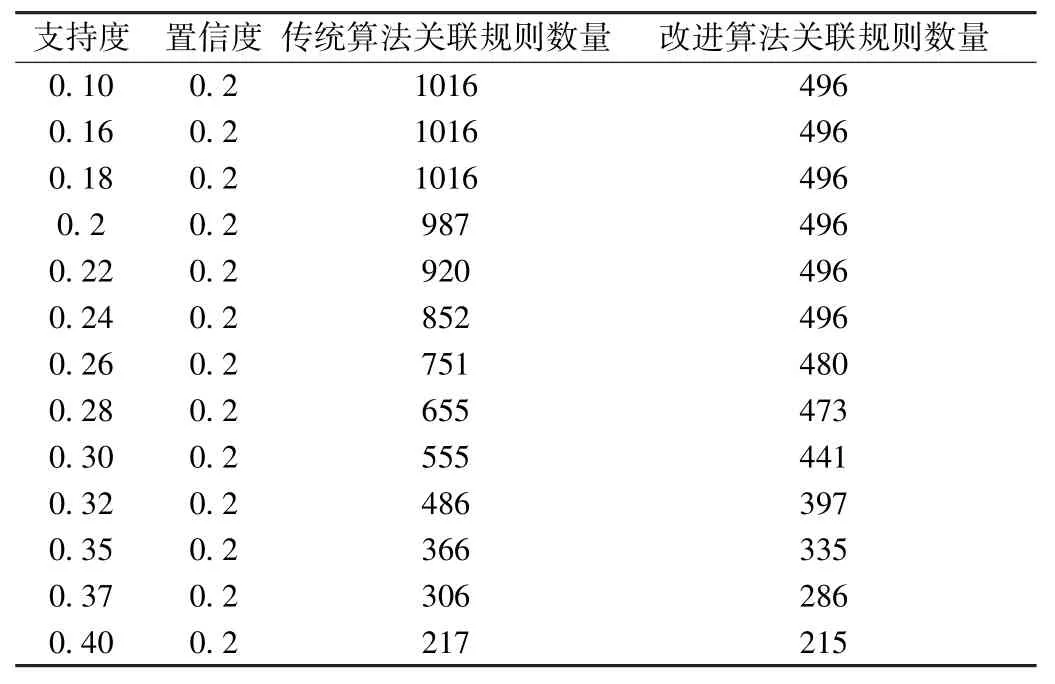
表4 置信度定值下各支持度输出关联规则数量

表5 支持度定值下各置信度输出关联规则数量

表4、表5 采用改进率指标客观衡量改进的Apriori 算法相对于传统算法在规则挖掘性能方面的提升程度，较大的改进率表明改进算法在关联规则挖掘性能方面相对于传统算法具有更大的提升，形式化定义如式（5）。根据改进率定义得到不同参数下两种算法的性能表现，如图1 所示，改进率均大于0，并且支持度阈值范围在0.10 ～0.18范围内，置信度阈值范围在0.1 ～0.3 范围内改进率达到最高，表明改进后的Apriori 算法支持度和置信度阈值在此范围内筛选强规则均优于传统挖掘规则算法，设置合适的置信度－支持度最小阈值可以有效滤除掉冗余规则，有效验证了改进算法在挖掘关联规则性能方面取得了显著的进步。并且通过图1 表明将支持度最小阈值取为0.18，置信度最小阈值取为0.20 时，改进算法的最小兴趣度阈值设置为0.50，最小提升度设置为1 时，挖掘强规则性能为最优，效能分别提升49.75%和51.19%。

图1 不同参数下两种算法性能比较

2.3 改进Apriori 算法关联规则

基于改进的Apriori 算法对成绩样本集进行关联规则挖掘共得到496 条强关联规则，根据提升度和兴趣度筛选出置信度、支持度、兴趣度、提升度参数值最高的前5 条绘制部分关联规则表。

表6 中置信度最高的前5 项关联规则表明超过90%的概率证明跨课程的知识应用使得学生能够在其他专业课程中将电路与电子学的理论应用于实践，并在处理知识细节时更加深入和精准，并且支持度和兴趣度均大于0.5，支持度最高达到0.72，提升度均大于1，表示5 门课程获优和电路电子学课程获优超过半数，并且这个现象都呈现出显著的正向趋势。

表6 置信度－部分关联规则表

表7 显示了支持度前5 的关联规则，并且前项和后项置信度都相对较高，说明课程间存在知识结构相似，课程之间存在相辅相成关系，并且规则1、2 和规则3、4 还表现出双向关联关系，学生学习这些课程过程中可能知识互相启发，双向受益。并且前4 条规则一定程度说明数字逻辑和电路，微机和电路具有较高的共现性，即涉及到这两门课程时成绩往往呈现出关联性，提醒任课教师应在平时教学过程中保持沟通，协同发力。

表7 支持度－部分关联规则表

从表8 可以看出传感器与其他课程之间的关联性具有显著的正向关系，提升度均大于1.30，分析得出传感器内容中涉及到的电路部分、程序编写部分、逻辑组成和通信部分在其他课程中均有细致讲解，所以传感器成绩与数字逻辑与数字系统、单片机等课程呈现相关关系，即传感器课程提供了单片机、计算机网络技术等课程的基础知识和技能。这就要求任课教师及时调整授课方式，在平时授课期间需结合领域专业和应用项目对传感器原理与应用进行课堂内容的扩充和发展。

表8 提升度－部分关联规则表

表9 给出了兴趣度较高的前5 条规则，兴趣度较高表示前项课程影响后项课程的考试等级，分析挖掘的规则1 和2 可以发现传感器获优的学生在逻辑电路、单片机（如51 和嵌入式）、计算机应用方面综合能力更强，可能此类学生在学科竞赛中积累了一定经验，反哺了课程的学习，达到了良性循环模式。但传感器课程获良的同学可能还欠缺实践环节，在单独的课程考试上成绩还可以，但并没有将所学课程综合应用，所以此类学生逻辑电路、计算机基础知识和程序编写有一定基础，但未能达优，此外规则4、5 揭示了计算机网络对数字逻辑与数字系统和传感器原理与应用等课程具有一定因果性，在实际教学过程中，计算机应用往往关联单片机和传感器进行课程设计和课程实验等，在一定程度上也验证了挖掘规则的有效性。

表9 兴趣度－部分关联规则表

3 结语

成绩挖掘在高校成绩分析中的应用可以帮助高校更好地了解学生表现、优化课堂管理、个性化教学，为教师决策和学生发展提供科学依据，进而提升教育质量和学生综合素质。本文在此前提下进行了相关研究，采用添加提升度和兴趣度改进的Apriori 算法对成绩样本进行挖掘关联规则，同时和传统的挖掘算法进行了对比，结果表明改进算法的性能方面具有更大的提升；最后对挖掘规则筛选出的各参数值最大的前5 条规则进行分析，对学生在不同课程中的表现模式背后的原因进行分析，针对性地给出学生提高专业课程的建议。