双有源桥型电力电子变压器电磁暂态实时低耗等效模型

高晨祥，林丹颖，韩林洁，冯谟可，许建中，李彬彬

（1.新能源电力系统国家重点实验室（华北电力大学），北京市 102206；2.哈尔滨工业大学电气工程及自动化学院，黑龙江省哈尔滨市 150001）

0 引言

电力电子变压器（power electronic transformer，PET）因其安全稳定的电压变换、可靠灵活的功率控制等功能，在当前大规模交直流混联、新能源汇集的电力系统发展需求下，展现出十分重要的理论研究与工程实用价值［1-3］。使用高频链（high frequency link，HFL）隔 离 的 双 有 源 桥（dual active bridge，DAB）型PET 是其中的关键设备之一［4］。

电磁暂态（electromagnetic transient，EMT）实时仿真具备效率高、可控制器硬件在环调试等诸多优势，已成为设备级效率、功率密度、经济性测试，以及电网级在线分析、故障预演等方面研究分析的重要工具［5-7］。随着PET 在配电网中的应用，其实时仿真研究受到广泛关注。当前，PET 的电磁暂态实时仿真研究面临以下困难和挑战［8-11］：

1）高频链的工作频率日渐提高，为实现对高频瞬态过程的精确拟合，实时仿真过程中要求采用很小的仿真步长，常为最小开关周期的1/100～1/20［12-13］（1 μs 及以下）。这要求PET 的实时仿真模型具有很好的并行性和低仿真延时。

2）模块结构复杂，模块间拓扑连接方式多样［14］，导致了很高的计算复杂度。但是，实时仿真硬件平台，如现场可编程门阵列（fieldprogrammable gate array，FPGA）等，硬件资源有限，限制了仿真规模。

3）模块化级联的结构使得PET 节点导纳矩阵的阶数很高，且开关器件多。网络解算过程中，面临大量的大规模矩阵存储，对内存要求较高。

目前，针对PET 实时仿真的研究按开关器件的建模方法，可分为以下3 类：

1）基于L/C 定导纳开关模型的实时仿真。L/C模型具有节点导纳矩阵不随开关状态改变的优良特性［15-17］，被广泛应用于主流的商用实时仿真软件，如RTDS、RT-LAB。文献［18］基于RT-LAB 的库元件和eHS 解算器，搭建了包含3 个DAB 模块的800 ns PET 实时仿真模型。为解决高频情况下L/C 模型的虚拟功率损耗问题，文献［19-21］提出了基于响应匹配的广义L/C 模型，实现了3 个DAB 模块的250 ns 实时仿真及硬件在环测试。相比于基于常规L/C 开关的实时模型，该模型在仿真精度方面得到极大提高。但是，其对仿真资源的需求相对较高，仿真规模问题尚未得到很好解决。

2）基于二值电阻开关模型的实时仿真。二值电阻模型可准确反映电力电子装备的系统级特性，被广泛应用于PSCAD/EMTDC 等离线仿真软件中［22］，但是存在由开关状态切换引起的节点导纳矩阵时变问题。在实时仿真过程中通常引入矩阵预计算与存储过程来克服这一问题。文献［9］基于模态划分和节点导纳逆矩阵存储，实现了单个LLC 谐振变换器25 ns（5 个时钟）实时仿真。文献［11］通过将矩阵存储与分层并行技术结合，实现了42 个DAB模块实时仿真。但是，当开关数量和节点数量较多时，内存需求量将急剧增加，仍面临仿真规模受限问题。

3）基于理想开关函数的实时仿真。文献［23-24］通过对高频链单元的分析，将开关器件的导通关断表征为理想开关函数，进而交直流侧的相互影响可以由受控电压、电流源的形式体现。这种方法避免了L/C 开关模型中的虚拟功率损耗问题和二值电阻开关模型的节点导纳矩阵时变问题，但是这种模型不能反映真实的换流单元器件损耗、压降等特征，并且受控源控制信号的产生和赋值会给电路部分带来一个时间步长的延时，影响仿真精度。

总体而言，当前PET 实时仿真方法仍面临计算延时高、资源消耗多、内存占用大等方面的问题，为适应大容量模块级联场景的实时仿真需求，需进一步开展PET 电磁暂态实时仿真算法研究。

本文借鉴文献［25］中“高频链端口解耦”的思路，提出一种DAB 型PET 实时低耗等效建模算法。首先，深入挖掘了DAB 高频链端口解耦模型输入导纳的二值特性，给出了其数值和物理解释，构建了具有N+1 特性的PET 高频链端口解耦模型，为实时仿真提供算法支撑。其次，为降低对实时仿真内存、计算时钟、硬件资源3 个方面的需求，利用DAB 模块等值参数的二值特性，提出基于有限存储的低内存占用EMT 解算方案；通过紧凑型计算逻辑，实现低延时实时仿真框架构建；利用等效算法的高度并行性，提出多模块分组并行的流水线结构。最后，基于Verilog 语言，完成RT-LAB 实时等效仿真模型的开发，通过与PSCAD/EMTDC 中详细模型的对比，验证实时等效建模算法的精度，并进行了多模块资源利用率测试。

1 DAB 型PET 高频链端口解耦等效模型

1.1 拓扑及工作原理

DAB 型PET 电路拓扑如图1 所示，务模块采用输入串联输出并联（input series output parallel，ISOP）方式连接，其传输功率通过移相角控制［26］。图中：MVDC 和LVDC 分别表示中压直流和低压直流；LT为变压器电感；k为变压器变比。

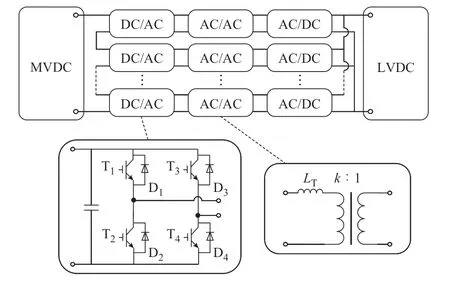
图1 DAB 型PET 拓扑Fig.1 Topology of DAB-based PET

采用二值电阻模型对绝缘栅双极晶体管（IGBT）/二极管开关组进行等值，采用后退欧拉法离散电容、电感和变压器，所得DAB 模块伴随电路如图2 所示。

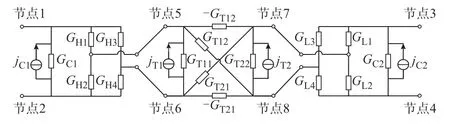
图2 DAB 模块伴随电路Fig.2 Companion circuit of DAB module

图2 中的GH1～GH4和GL1～GL4为二值导纳值，其他部分参数表达式如式（1）所示［25］。

式中：L1、L2和Lm为变压器电感参数；Δt为仿真步长；GCi、jCi和GT、jTi分别为电容和变压器的等效导纳和等效历史电流源；Ci为端口电容；vCi为电容电压；iTi为变压器电感电流。

1.2 PET 模块端口解耦等效模型

DAB 模块等效电路可通过消去如图2 所示的节点5～8 获得，其简要步骤如下。首先，对DAB 模块列写节点导纳方程，并表示为分块矩阵的形式：

式中：JEX、IEX分别为外部节点的注入历史电流列向量和独立电流列向量；JIN为内部节点的注入历史电流列向量；VEX和VIN分别为外部节点和内部节点的电压列向量；A、B、C均为节点导纳矩阵的分块子矩阵。

其次，利用嵌套快速求解法消去式（2）中内部节点电压VIN，有

由文献［25］可知，式（3）所得等效节点导纳方程具有如下特征：

式 中：y11、y12、y21、y22为 节 点 导 纳 矩 阵 的 特 征 元 素；v1～v4为4 个外端子节点的电压；jS1、jS2为短路电流列向量的特征元素；i1、i2为DAB模块两侧端口的电流。

这一特性产生的原因是，DAB 模块包含隔离变压器，满足严格的端口条件，其节点导纳矩阵表达存在冗余。式（4）所示4 阶等效节点导纳方程可用如式（5）所示的2 阶短路导纳参数（Y 参数）方程，即端口方程表示。

式中：vIN、iIN和vOUT、iOUT分别为DAB 模块输入侧和输出侧的电压、电流；YAB和YDAB22为端口的输入导纳；YAB=YAB为转移导纳；iSC1和iSC2为外端口短路时的2 个端口的短路电流。务参数具有直观的物理意义，其等效电路如附录A 图A1 所示。

式（5）中DAB 模块等效电路务参数可由附录B 式（B1）所示代数运算获得［25］。其中，q1～q5为常数，如附录B 式（B2）所示，由式（1）所示变压器等效导纳GT11、GT12、GT21、GT22和开关器件的二值导纳GON、GOFF决定。KAB～KAB为符号函数，由图2 所示 的8 个 二 值 导 纳GH1～GH4、GL1～GL4的 控 制 信 号TH1～TH4、TL1～TL4决定，如式（6）所示。

在这一双端口等效电路基础上，为便于DAB 模块级联，本文采用文献［25］所提高频链端口解耦算法，将式（5）和附录A 图A1 所示DAB 等效电路进行电容电压约等，所得DAB 模块端口方程如式（7）所示。

式中：jeq1和jeq2为2 个端口的诺顿等效历史电流源。

DAB 模块高频链解耦等效电路如图3（a）所示，该方法的仿真精度与数值稳定性已在文献［25，27］中得到证明。

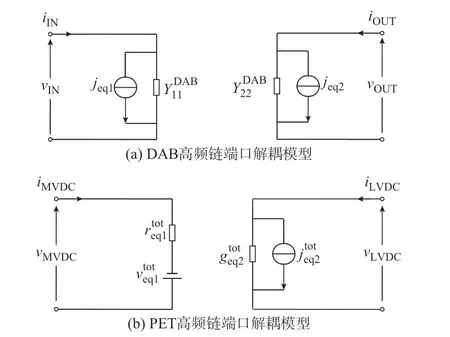
图3 高频链端口解耦等效模型Fig.3 Decoupling equivalent model of high-frequency link port

将输入侧诺顿等效电路转化为戴维南等效电路，并进行串并联侧模块等效参数的求和，可得PET 高频链端口解耦模型如图3（b）所示，务参数表达式如式（8）所示。

式中：r和v分别为PET 输入侧等效戴维南电阻和电压源；g和分别为PET 输出侧诺顿等效电导和电流源；req1，i和veq1，i分别为第i个模块的等效戴维 南电阻和电压源；geq2，i和jeq1，i、jeq2，i分别为第i个模块的诺顿等效电导和电流源；N为DAB 模块数；Y和Y为 第i个DAB 模 块 的 二 端 口 输 入导纳。

1.3 DAB 端口解耦模型二值特性及PET 端口解耦模型“N+1”特性

由附录B 式（B1）可知，DAB 模块的端口输入导纳YAB和YAB具有二值特性，由其相邻H 桥控制信号决定，可记其表达式如下：

式中：Q1～Q4为常数，可在程序开始计算获得和分别表示KAB和KAB的逻辑非。

1.2 节给出了DAB 模块二端口等效电路的输入导纳二值特性的数值解释。为进一步揭示二值特性产生的原因，本节从等效电路构建角度对其物理意义进行阐述与分析。

由Y 参数定义可得，DAB 模块二端口等效电路输入导纳YAB和YAB可以通过将对侧端口短路，内部电流源置零后，求务端口电流与电压之比获得，如式（10）所示。

以YB为例，其获取过程如附录A 图A2 所示。其 中，GT11、GT12、GT22为 变 压 器 等 效 导 纳，GC1和GC2为电容的等效电导，如式（1）所示，均为常数。GH1～GH4、GL1～GL4为 由 触 发 信 号TH1～TH4、TL1～TL4控制的二值导纳值，具有时变特性。

在非闭锁运行状态下，DAB 模块的H 桥同桥臂互补，故有：

式中：GON通常取100 S；GOFF通常取1e-6S。

因此，附录A 图A2 右侧粉色框内电路的等效电导Yeq1恒定为：

GT11、GT12、GT22为定值，故左侧H 桥交流端口等效电导Yeq2也恒定。YDAB11仅由其相邻H 桥触发信号TH1～TH4决定，分为TH1≠TH3和TH1=TH3两种情况，可表示为：

同理，有

该结论与由直接数值计算所得式（9）一致。

综上，虽然DAB 模块包含8 个IGBT/二极管反并联开关组，但由于H 桥固定的拓扑结构和开关方式，其输入导纳并不会有28种可能情况，而是表现为由同侧H 桥开关信号决定的二值特性。

利用单模块输入导纳的二值特性，将式（9）代入式（8）可得：

式 中：n1和n2分 别 表 示 满 足TH1≠TH3和TL1≠TL3的DAB 模块数，n1，n2∈{0，1，…，N}。

因此，包含N个模块的PET 系统，其输入电阻r和输出电导g仅有N+1 种可能取值，可通过参数存储和对触发信号的逻辑判断直接获取。

1.4 内部信息更新

将图3（b）所示的PET 等效模型与外电路结合，进行EMT 解算结束之后，可获得中压直流母线电压vMVDC、电流iMVDC和低压直流母线电压vLVDC、电流iLVDC，如图3（b）所示。然后，需要对务模块端口及内部节点电压进行更新，用于下一步长的迭代计算。

务模块共用输入侧电流iIN=iMVDC和输出侧电压vOUT=vLVDC。因此，务模块端口电压（即电容电压）表达式为：

式中：veq1为模块输入侧戴维南等效电压源，如式（8）所示。

在文献［25］中，变压器端口电压vT1和vT2的更新仍需要进行矩阵乘法与求逆运算，会给实时仿真带来较大负担。本节将DAB 模块等效电路参数求解过程中节点导纳方程预处理的思想引入对变压器端口电压的更新过程中，所得端口电压更新式如下：

其中，仅包含对常数与符号函数的代数运算，计算负荷大幅简化，更便于实时仿真的实现。

2 DAB 型PET 实时低耗等效仿真算法

2.1 基于有限导纳存储的低内存占用EMT 解算

基于二值开关电阻模型的电力电子系统在执行EMT 解算时，面临节点导纳矩阵时变问题，需进行大量矩阵乘法与求逆运算，不利于实时仿真的实现。因此，本节提出一种基于有限导纳存储的低内存占用EMT 解算方案。

为便于EMT 解算描述，设DAB 型PET 输入侧的外电路为戴维南等效电路（包含戴维南等效电阻rEX1和等效电压源vEX1），输出侧外电路为诺顿等效电路（包含诺顿等效电导gEX2和等效电流源iEX2），结合图3（b）所示PET 高频链端口解耦模型，可得EMT 解算电路如图4 所示。

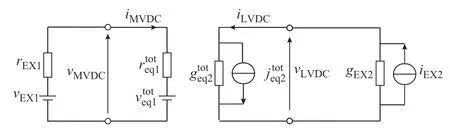
图4 EMT 解算等效电路Fig.4 Equivalent circuit for EMT solving

求解该电路可得：

从式（18）和式（19）可知，一方面，PET 的高频链解耦等效模型仅包含2 条支路、4 个节点，使得EMT 解算矩阵阶数大幅减小，降低了求解复杂度；另一方面，由式（15）所示PET 等值电阻/电导的N+1 特性可知，式（18）和式（19）中系数矩阵也通过有限的参数存储（6N+6 个）来避免除法运算，可大幅减小对存储量的需求。

当系统外电路复杂时，其EMT 解算系数矩阵仍可用少量内存占用实现节点导纳逆矩阵的存储，从而使得二值电阻开关模型可以用于大规模DAB型PET 系统的实时仿真中。

2.2 电磁暂态等效算法的矩阵表达

为方便实时仿真算法逻辑的实现，本节分别对DAB 型PET 等 效 电 路 参 数 求 解、EMT 解 算、内 部信息更新3 个过程进行梳理，建立其矩阵表达形式。

1）等效电路参数求解

由2.1 节可知，DAB 模块等效参数计算仅包含串联侧等效历史电压源和并联侧等效历史电流源的求解，记为veq1和jeq2。将式（1）和附录B 式（B1）代入式（7）可得附录B 式（B3），记为：

式中：Seq=［veq1，jeq2］T为DAB 模块等效历史源列向量；iT为变压器原副边电流向量；vC为电容电压向量；P1和P2为由常数与符号函数决定的系数矩阵。之后，按照式（8）对务模块等效历史电压/电流源求和，即可获得PET 的等效电路参数。

2）EMT 解算

记式（18）和式（19）所示EMT 解算过程为：

式中：SMVDC=［vMVDC，iMVDC］T和SLVDC=［vLVDC，iLVDC］T分别为PET 输入和输出端口电压、电流信息；vS，EQ和iS，EQ分别为外部独立源与等效历史源；P3和P4为2 阶系数矩阵。

3）内部信息更新

记式（16）所示模块电容端口电压更新表达式为：

式中：SIO=［iIN，vOUT］T=［iMVDC，vLVDC］T，由式（21）获得；P5和P6分别为2×2 和2×1 的系数矩阵。

变压器端口电压更新表达式如式（17）所示，将式（1）和式（22）代入式（17），可得附录B 式（B4）所示具体表达式，记为：

式中：vT=［vT1，vT2］T为变压器原副边电压；P7～P9为系数矩阵，务元素均可通过常数与符号函数的逻辑运算得到。

由图2 可知，变压器电流表达式为：

式中：jT=［jT1，jT2］T为变压器原副边等效历史电流源，如图1 所示；E为单位矩阵；P10～P12为系数矩阵，务元素均可通过常数与符号函数的逻辑运算得到。

综合式（22）—式（24），可列写内部电气信息反演过程矩阵表达式如下：

2.3 基于紧凑型计算逻辑的低延时仿真框架

按2.2 节中3 个步骤绘制数据流图，如图5（a）所示。图中：TK=［TH1，TH3，TL1，TL3］为触发信号组，用于表征务模块控制信号；∑表示将务模块等效电压、电流源逐个累加，如式（8）所示。

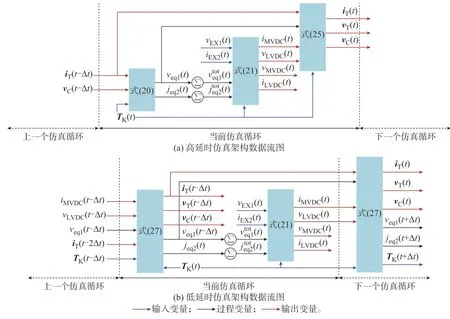
图5 实时仿真数据流图Fig.5 Data flow diagram of real-time simulation

图5（a）所示的算法框架与离线仿真平台PSCAD/EMTDC 类似，在每一步长仿真中均包含3 个阶段：电力网络等值参数计算，如式（20）所示；电力网络求解，如式（21）所示；计算结果输出与电气信息更新，如式（25）所示。这3 个步骤在PSCAD仿真流程中分别对应DSDYN、EMTDC 解算、DSDOUT 这3 个环节［28］。同时，这3 个阶段需要串行执行，延时较长。

为缩短实时仿真每步的时钟消耗，本节提出一种基于紧凑型计算逻辑的低延时仿真框架。

首先，考虑到PET 外电路的复杂性，保留以戴维南/诺顿等效电路参与EMT 解算的独立过程，即维持式（21）所示EMT 解算不变。当外电路改变，只需对这一部分进行修改即可。

其次，上一步的内部电气信息更新结果为下一步的等值参数计算的输入。因此，可将式（25）代入式（20）得：

式中：P13～P15为由P1～P12计算所得的参数矩阵。

式（25）和式（26）共用输入变量，可将两式合并：

所提低延时仿真架构的数据流图如图5（b）所示，上一步的内部电气信息更新与下一步的等值电压、电流源计算并行执行，在不损失仿真精度的同时，缩短了所需时钟数。

3 实时仿真硬件实现

3.1 数据格式

浮点数和定点数为FPGA 常用的两种数据格式。浮点数数据范围广、精度高、存储需求小，定点数加法执行便捷、时钟消耗少。因此，本文使用浮点数与定点数混合的数据表示方法。乘法运算使用32 位IEEE 754 标准的浮点数实现，每个乘法器占用2 个DSP48E 资源；加减法运算使用60 位定点数（24 位整数、36 位小数）实现，占用一定的逻辑片资源；数据的存储以浮点数格式完成，减少内存消耗。浮点数与定点数之间的相互转换可通过Xilinx 自带的IP 核（intellectual property core）实现。

3.2 矩阵-向量乘法的实现

如图5（b）所示，本文所提PET 实时低耗仿真算法仅包含式（27）所示的1 个8×5 矩阵乘法和式（21）所示的2 个2×2 矩阵乘法。经典的FPGA 矩阵-向量乘法（matrix-vector multiplication，MVM）实现方式如附录A 图A3（a）所示，可通过m个乘法器经n+1 个时钟实现m×n矩阵A与n维列向量b的乘法［20-21］。

考虑矩阵中的0、1、-1 元素乘法可直接由逻辑运算获得，式（21）与式（27）所示低阶矩阵中仅分别包含8 次和31 次乘法运算。为节省时钟占用，本文采用如附录A 图A3（b）所示的代数乘法方式，将矩阵-向量运算中的所有乘法运算在一个时钟直接完成。同时，由于所需存储的矩阵元素很少，可直接使用寄存器代替只读存储器（ROM）存储。

该方法增加了对DSP48E 资源的消耗，但由于乘法运算很少，DSP48E 并不会成为制约仿真规模的主要因素。该结论将在4.3 节中予以验证。

3.3 多模块分组并行的流水线设计

在获得务DAB 模型输入侧的戴维南等效电压和输出侧的诺顿等效电流源后，需要对其进行求和运算，如式（8）所示。综合考虑仿真资源与时钟需求，本文设计了如图6（a）所示的分组并行流水线计算方案。该方案包含m个等值参数计算模块（equivalent parameter calculation module，EP-CM）和1 个EMT 解 算 模 块（EMT calculation module，EMT-CM），如图6（b）和（c）所示。图中：Z-Δt表示控制器触发延时。

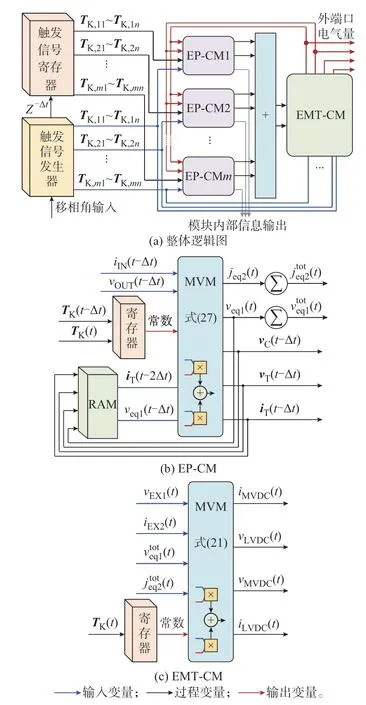
图6 分组并行流水线计算方法的硬件实现Fig.6 Hardware implementation of packet-based parallel pipeline computing method

首先，FPGA 中的触发信号生成器接受上位机输入的移相控制信号，生成务DAB 模块的触发信号组TK，并将其分为m组，记第i组信号为TK，i1～TK，in（i∈[1，m]）。其次，每组第1～n个DAB 模块的TK，ij（j∈[1，n]）按照时钟被依次并行送入对应的第i个EP-CM 模块，进行如式（27）所示的计算，实现流水线作业。组内务DAB 模块等效电压/电流源的求和分别在务自EP-CM 模块内部完成。然后，务流水线所得求和结果经加法器合并，完成DAB 型PET 等效电路参数的求解。最后，由EMT-CM 模块完成式（21）所示电路解算功能。

通过上述方案，包含N=m×n个DAB 模块的PET 系统的单步仿真可在17+n个时钟内完成，硬件资源占用量将随m线性增加。同时，用户可以根据仿真步长与硬件资源的实际需求与限制，灵活调整m和n的取值，获得最优仿真方案。

4 仿真验证

4.1 仿真环境

为验证所提DAB 型PET 实时低耗等效仿真算法的有效性，本文在RT-LAB 上基于Verilog 语言开发了PET 实时等效仿真模型，平台架构如附录A 图A4 所示。

PC 机上配置RT-LAB 仿真软件，仿真机使用OP5700，内含一台32 位Intel Xeon E5 CPU 处理器和一块Xilinx Virtex-7 FPGA、485T 板卡，FPGA 时钟频率为100 MHz。CPU 处理器用于移相角生成；FPGA 完成脉宽调制（PWM）信号生成和主电路解算。PC 机与OP5700 之间通过TCP/IP 协议通信，OP5700 内部的CPU 与FPGA 之间通过PCIE 协议通信。为方便后续模型的扩展，本文设置CPU 控制系统步长为10 μs，FPGA 侧实时等效模型仿真步长为250 ns。

4.2 仿真精度测试

本节搭建DAB 型PET 实时等效模型，与使用PSCAD/EMTDC 库元件构建的详细模型进行对比，系统参数如表1 所示。PET 的输入侧采用戴维南等效电路，输出侧采用电阻负载，控制方式为双移相控制，内移相角设置恒定值为9°。

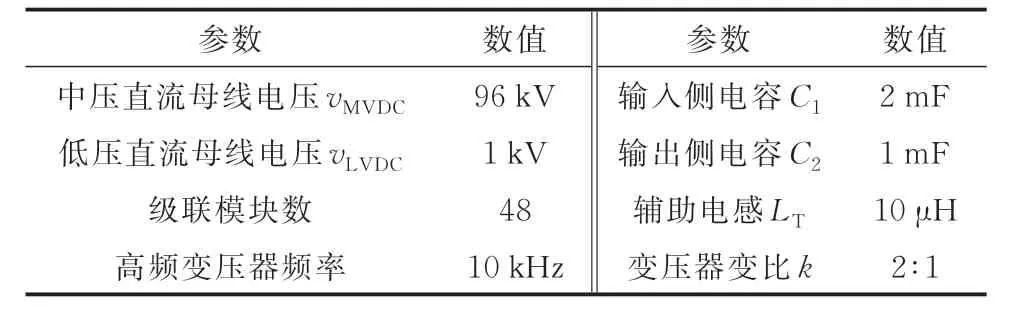
表1 实时仿真系统参数Table 1 Parameters of real-time simulation system

设置系统工况如下：

1）0～0.2 s，系统启动，负载电阻为0.5 Ω，vLVDC参考值为1.0 p.u.；

2）0.2～0.4 s，稳态运行；

3）0.4 s，功率跃变，vLVDC参考值降低为0.8 p.u.；

4）0.7 s，负 载 突 变，负 载 电 阻 由0.5 Ω 突 变 为0.25 Ω；

5） 1 s，仿真结束。

不同工况下，PSCAD 离线详细模型与实时等效模型的低压直流母线电压vLVDC波形如附录A 图A5 所示。在务过程中，最大相对误差如下：1）启动阶段，vLVDC经0.14 s 上升到参考值1 kV，最大相对误差为1.3%；2）0.4 s 输出电压参考值改变，经短暂过渡过程，系统进入新的稳态，vLVDC变为0.8 kV，最大相对误差为1.8%；3）0.7 s 负载突变时，vLVDC急速下降，两类模型最低点电压分别为0.647 kV 和0.648 kV，最大相对误差为1.5%。

为反映所建实时等效模型对系统内部特性的拟合效果，绘制变压器电压、电流波形如附录A 图A6所示。由图可知，所建实时等效模型变压器电压、电流波形与离线详细模型基本一致，最大相对误差小于2%。同时，变压器电压为近似矩形波，不会出现L/C 模型虚拟损耗导致的波形畸变。

4.3 资源消耗测试

为测试本文所提实时低耗仿真方法的资源占用率，本节建立不同模块数DAB 型PET 250 ns 实时等效仿真模型，测试其务类资源占用，如表2 所示。绘制其务类资源占比图，如图7 所示。

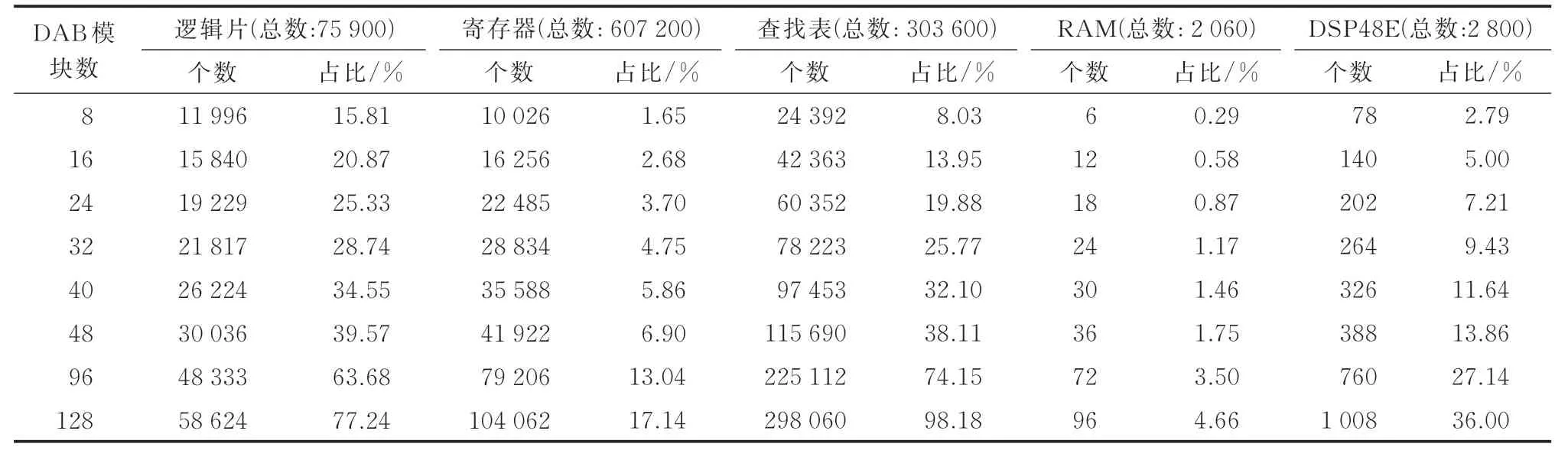
表2 不同DAB 模块数PET 实时仿真硬件资源占用Table 2 Hardware resource occupancy of real-time simulation for PET with different numbers of DAB modules

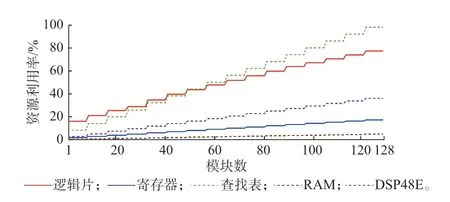
图7 PET 实时仿真硬件资源利用率Fig.7 Hardware resource utilization of real-time simulation for PET

由于FPGA 主频为100 MHz，实时仿真系统步长为250 ns，即每个仿真步长应在25 个时钟内完成。由3.3 节可知，本文所提分组并行解算模式下，单步长仿真消耗时钟为17+n，故n=8，如图6 所示的每个等值参数计算模块最多可执行8 个模块的解算。因此，本节测试模块数取8 的整数倍，即使实际模块数不足8 的整数倍，也应按整数倍确定资源。

由图7 和表2 数据可知，随着模块数的上升，务类资源均呈现阶梯线性增加。每增加8 个DAB 模块（即一个等值参数计算模块），逻辑片（Slice）资源增加3 100 个（4.08%），寄存器（Register）资源约增加6 300 个（1.04%），查找表（LUT）资源约增加18 244 个（6.01%），随机存取存储器（RAM）资源增加6 个（0.29%），乘法器DSP48E 资源增加62 个（2.21%）。

因此，RAM 资源与乘法器DSP48E 资源占用很少，不是限制仿真规模的主要因素。查找表资源与逻辑片资源增加较快，当模块数达128 时，查找表资源占用达98.18%，仿真规模无法继续增加。

4.4 算法性能分析

本文所提实时低耗等效建模方法借鉴了文献［25］节点导纳方程预处理与电容端口解耦的思路，获得了仅包含4 个外端子节点、2 条支路的PET等效电路。区别于文献［25］，所提方法考虑了PET实时仿真模型对存储内存、仿真延时、硬件资源的需求，进行了如下优化设计。

1）基于有限导纳存储的低内存占用EMT 解算方案。利用DAB 模块拓扑及控制特征，构建了如图3（a）所示的单个DAB 模块等值电路，其等效电导表现为受开关信号控制的二值特性；接着，构建N个DAB 模块的PET 高频链端口解耦等效模型，如图3（b）所示，输入电阻和输出电导务仅有N+1 种可能取值。同时，大规模节点的EMT 解算过程被等效为如式（18）和式（19）所示的低阶矩阵解算。在此基础上，通过有限的导纳逆矩阵存储，有效克服了由开关信号二值电阻模型带来的节点导纳矩阵时变问题。

2）基于紧凑型计算逻辑的低延时仿真框架。通过对等值计算流程的矩阵化梳理与运算，将传统EMT 解算的“电力网络参数计算”“电力网络求解”“网络内部电气信息更新”3 个步骤中，前一时步“网络内部电气信息更新”和后一时步的“电力网络参数计算”2 个步骤并行，获得了低延时仿真框架如图5（b）所示，大幅缩减了仿真耗时。

3）多模块分组并行的流水线设计。利用务模块等效电路求解过程的高度可并行性，将模块分组和流水线排列，通过时分复用的方式，使得同组内不同模块的解算过程共用相同的计算资源，有效降低了对计算硬件资源的需求。

需要注意的是，本文所提实时低耗等效建模算法围绕ISOP 型DAB 高频链展开，该算法同样可适用于其他模块类型和拓扑连接方式的PET 系统。同时，上述存储内存、仿真延时、硬件资源方面的优化方法也可为其他电力电子系统的实时仿真提供参考。

为进一步揭示本文所提实时低耗等效建模方案与其他实时仿真方法的区别，本节对比了文献［18］所提基于RT-LAB 的库元件和eHS 解算器的详细仿真模型（detailed model，DM）、文献［20］所提基于响应匹配和紧凑型EMT 解算框架的PET 等效模型（equivalent model 1，EM1）、文献［11］所提高并行度等效模型（EM2）以及本文所提低耗等效模型（lowconsumption equivalent model，LEM），对比结果如表3 和表4 所示。

表3 不同PET 实时仿真模型具体指标对比Table 3 Comparison of specific indicators of different real-time simulation models for PET

表4 不同PET 实时仿真模型整体性能对比Table 4 Comparison of overall performance of different real-time simulation models for PET

在仿真精度方面，DM 采用L/C 开关模型，EM1采用了基于响应匹配算法的L/C 模型，受限于虚拟功率损耗问题，其精度低于采用二值电阻模型的EM2 和LEM。在大规模系统仿真能力方面，DM 模型和EM1 模型仅可支持数个DAB 模块规模的仿真，仿真规模受限，EM2 模型最大单板可支持50 个模块左右的仿真，而本文所提LEM 由于硬件资源和存储内存等方面的优化，最大仿真规模可达上百模块。在高频系统仿真能力方面，DM 模型的最小仿真步长为800 ns，但高频段下L/C 模型虚拟功率损耗问题更加严重，适用性受限；EM1、EM2 和LEM模型最小仿真步长可限制在400 ns 以下，可有效支持高频DAB 的仿真。在可扩展性方面，DM 由于基于分立元件构建，可灵活修改拓扑，EM1、EM2 和LEM 需要对给定拓扑进行等值处理，可扩展性略低。

5 结语

本文通过数值计算和物理意义分析，证明了DAB 模块高频链端口等效模型输入导纳具有二值特性，在此基础上构建了具有“N+1”特性的PET高频链端口解耦模型。DAB 型PET 的这一特性表明，对于拓扑和参数固定的电力电子系统，其外端口等效电路的导纳/阻抗仅包含有限可能解，通过外端口等效模型构建和等效参数分析，可以有效解决二值开关电阻模型引起的导纳时变问题，为大规模电力电子系统的实时仿真提供算法支撑。

本文提出了基于有限导纳存储的低内存占用EMT 解算方案、紧凑型计算逻辑的低延时仿真框架、多模块分组并行的流水线设计，可有效降低PET 实时仿真模型对存储内存、仿真时钟、硬件资源的要求。该设计思路和框架可为其他模块化级联拓扑的实时仿真提供借鉴。

本文所提实时仿真方法仅适用于DAB 型PET非闭锁工况的仿真，其闭锁工况需要考虑二极管的插值等过程，有待进一步解决。同时，诸如多有源桥型PET、大规模新能源经电压源变流器并网系统的其他更复杂的电力电子系统的实时仿真方法有待进一步探索。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。