基于改进联邦竞争深度Q 网络的多微网能量管理策略

2024-04-30黎海涛刘伊然杨艳红谢冬雪

电力系统自动化 2024年8期

黎海涛，刘伊然，杨艳红，肖浩，谢冬雪，裴玮

（1.北京工业大学信息学部，北京市 100124；2.中国科学院电工研究所，北京市 100190）

0 引言

作为接纳可再生能源高渗透率的理想平台，微网（microgrid，MG）将在推进碳中和、实现可持续发展中发挥重要作用［1-2］。为降低发电风险，多个相邻的MG 相互连接以形成MG 群，能够提升发电容量且降低供电风险。MG 群的结构复杂，对其进行能量管理面临较大挑战，研究有效的能量管理策略至关重要。但传统基于模型的能量管理策略仅适用于解决预定的调度问题，难以处理负荷需求意外变化的情况［3-5］。为解决此问题，有研究提出了基于深度强化学习（deep reinforcement learning，DRL）的方法。例如，文献［6］基于ɛ-greedy、soft-max 和置信区间上界等算法，提出基于多智能体DRL 的MG 能量管理方法，有效提升了MG 能量的自给自足性。文献［7］提出了一种基于多智能体深度确定性策略梯度的能量交易算法，降低了MG 管理的能耗成本。文献［8］以提高MG 系统收益为目标，利用深度Q 网络（deep Q-network，DQN）算法研究了分布式MG的灾后恢复管理问题，验证了多智能体DRL 在不同运行环境中均有很强的适应性。文献［9］提出基于强化学习（deep learning，DL）的MG 分布式二次最优控制方法，提高了每个MG 的自主性和适应性。针对区域MG 的分布式能源管理和策略优化，文献［10］提出一种集中训练、分布式执行的多智能体DQN 算法，保证了MG 群中每个参与者的利益且提高了MG 运行性能。

上述基于多智能体DRL 的MG 能量管理研究中，为了训练具有高泛化性的智能体模型，通常需要每个MG 提供大量的本地数据进行模型训练，然而每个MG 通常属于不同的实体，涉及数据安全问题。将具有数据隐私保护特性的联邦学习（federated learning，FL）应用于MG 能量管理，是解决该问题的一种可行技术途径。文献［11］提出基于Actor-Critic 的联邦DRL 的MG 能量管理算法，有效保护了数据隐私。文献［12］提出基于联邦DQN 算法的居民社区综合能源系统协同训练方法，能够优化务能源系统的经济效益及模型训练效率。文献［13］提出基于区块链的FL 算法，能有效预测MG 中能量生产和负荷需求，有效降低MG 的运行成本。目前基于联邦DRL 的MG 能量管理研究主要聚焦于电能方面，未考虑复杂的多类型能量转换以及不同MG之间的电量交易问题。同时，FL 框架中本地MG 和中心服务器之间需要频繁交互模型参数而耗费大量通信时间。

基于此，本文针对包含风、光、电、气、热的综合MG 系统，构建其能量管理的时序马尔可夫决策过程（Markov decision process，MDP）模型，提出基于正余弦算法（sine cosine algorithm，SCA）的改进联邦竞争深度Q 网络（Dueling DQN）算法，并利用该算法设计了计及MG 内部多能转换与外部能量交易的能量管理策略。在保证策略安全及数据隐私的前提下，能有效提升MG 运行的经济效益，并降低通信时延。

1 多MG 能量管理模型

考虑由多MG 组成的MG 群系统，见图1。

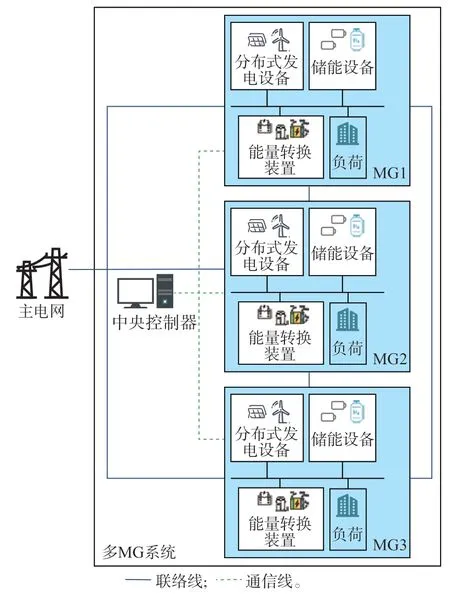
图1 多MG 系统结构Fig.1 Architecture of multi-MG system

务MG 既可与主电网进行电量交易，从外部网络购买天然气，也可与其他MG 进行电量交易，即每个MG 可以在其发电量超过需求时主动出售电量，或在发电量不足时从其他MG 购电。整个MG 系统以经济收益为目标，能量管理平台根据每个MG 中分布式发电设备的发电功率、电力负荷的用电功率和热负荷的热需求量，进行能量管理优化，进而获得较好经济收益［14-16］。

1.1 单MG 系统模型

多MG 系统中，每个MG 由分布式发电设备、储能设备、电力负荷设备、能量转换装置以及热负荷设备组成。

1.1.1 分布式发电设备

风能、太阳能等清洁能源的应用，加剧了能源市场的巨变，传统的化石能源占比逐渐降低。本文构建的MG 系统模型包括风能发电机和光伏发电站，可以根据天气状况选择不同的发电形式。不同于发电理论模型，本文分别采用来自芬兰风力发电厂的实际发电数据和美国得克萨斯州奥斯汀的光伏电站的实际发电数据作为分布式发电设备的输出。

1.1.2 储能设备

储能设备的功能主要是存储发电设备所产生的能量，其在MG 能量管理过程中与主电网、分布式发电设备、电力负荷设备以及热负荷设备进行能量交换。本文所建系统主要包括电池储能设备和氢气储能设备。电池储能设备的充/放电行为由MG 直接控制，并在充/放电行为的驱动下，与分布式发电设备、电力负荷设备进行能量交换。电池储能设备在时刻t的动态存储容量Be，t模型如下［17］。

式中：Ee，soc，t为电池储能设备在时刻t的荷电状态（state of charge，SOC）。

氢气储能设备，即储氢罐，主要用于存储氢气。氢气作为一种清洁能源，具有发电和加热的多功能性，在MG 中应用潜力巨大。氢气储能设备的充/放氢行为由MG 直接控制，并与分布式发电设备、电力负荷设备以及热负荷设备进行能量交换。氢气储能设备在时刻t的动态存储容量Bh2，t的数学模型为［18］：

式中：Bh2，t-1为氢气储能设备在时刻t－1 的存储容量；ηh2，C、ηh2，D分别为充、放氢效率系数；Qh2，t为时刻t的充氢或放氢速率；当Qh2，t＞0 时，0-1 变量I|Qh2，t＞0=1，表示氢气储能设备处于充氢状态；当Qh2，t≤0 时，0-1 变量I|Qh2，t≤0=1，表示氢气储能设备处于放氢状态；Qh2，max为氢气储能设备最大充放氢速率；Bh2，max为氢气储能设备最大容量。

式中：Eh2，SOC，t为氢气储能设备在时刻t的剩余气量。

1.1.3 电力负荷设备

随着科技的发展，不断涌现务种新型电力负荷，如直接可控负荷、恒温控制负荷、价格响应负荷和电动汽车负荷等［19-23］。本文主要对恒温控制负荷和价格响应负荷进行建模。

1）恒温控制负荷

包括空调、热水器、冰箱等需要恒温控制的负荷，通过开关切换来实现其工作状态变化，第v个恒温控制负荷在时刻t的动作ucontrol，v，t定义如下［16］，本文共设置2 个挡位。

式中：Tv，t为时刻t环境温度；Tv，max为设定的最高温度；Tv，min为设定的最低温度；ucontrol，v为恒温控制负荷的动作；v=1，2，…，NTCLs，其中，NTCLs为恒温控制负荷的数量。

第v个恒温控制负荷在时刻t的电力负荷PTCL，v，t如式（10）所示。

式中：PTCL为恒温控制负荷的标称功率。

2）价格响应负荷

价格响应负荷是指MG 中不能被直接控制且受电力价格影响的负荷。第u个价格响应负荷在时刻t的电力负荷Pload，u，t为：

式中：Pb，t为时刻t基本负荷的功率；Ou，t为时刻t的转移负荷；ζu为根据价格的增减而改变的负载率；ρb，t为时刻t的价格水平；Fu，t为［0，t-1］时间内所有转移负荷的和；u=1，2，…，Nloads，其中，Nloads为价格响应负荷的数量；τu，t′为判断是否从时刻t′转移负荷的0-1 变量，转移负荷时为1，否则为0。

1.1.4 能量转换设备

本文主要对恒温控制负荷和价格响应负荷进行建模。MG 系统设置能量转换装置来实现不同能量之间的转换。设定MG 配置电解槽、燃料电池和燃气锅炉3 类能量转换装置实现能量转换，其中，电解槽可使电能转换为氢能，燃料电池能将氢能转化为电能和热能，燃气锅炉可使氢能或天然气转换为热能，天然气是满足必要热量需求的备用燃料。定义能量转换函数表示能量转换装置中能量从流入到流出的转换映射规则［24］，利用该函数对3 类能量转换装置分别进行建模。式（12）—式（14）表示燃料电池和电解槽的能量转换功能，式（15）和式（16）表示燃气锅炉的转换过程，其中，MG 内的能量流如附录A 图A1 所示。

式中：Qh2，FC，t、Pe，FC，t、Qh，FC，t分别为燃料电池在时刻t的氢气流入量、电流出量、热流出量；ηe，FC、ηh，FC分别为燃料电池的电转换系数、热转换系数；Pe，WE，t、Qh2，WE，t、ηWE分别为电解槽在时刻t的电流入量、氢气流出量、转换系数；Qh2，GB，t、Qng，GB，t、Qh，GB，t分别为燃气锅炉在时刻t的氢气流入量、天然气流入量、热流出量；ηh2，GB、ηng，GB分别为燃气锅炉的氢气转换系数、天然气转换系数。

1.1.5 能量平衡约束

为使MG 的能量网络正常工作，在Δt∈[t，t+1]时段必须保障能量产生和消耗之间的平衡，设定MG 的电能、热能、氢能的平衡约束分别如下所示。

式中：ze，t为时刻tMG 电量交易量；PW，t为时刻t风力发电设备的发电功率；PPV，t为时刻t光伏发电设备的发电功率；Ptotal，e，t为时刻t电力负荷总功率；Ptotal，h，t为时刻t热负荷功率。Ptotal，h，tΔt表达的物理意义为热负荷在Δt时段内的总需求量。

1.2 单MG 的MDP 模型

对于单MG 系统，因为其运行环境及其状态满足马尔可夫属性，所以MG 能量管理和优化可以视为一个MDP［19，24］，并可用状态、动作、状态转移概率、奖励构成的四元组{s，a，p，r}来描述。下面具体描述MDP 模型的主要元组。

1）状态空间

MG 在时刻t的状态定义为：

式中：PTCL，t为时刻t NTCLs个恒温控制负荷功率的集合；ρdown，t为时刻t向电网销售电量的电价；ρup，t为时刻t从电网购买电量的电价。

2）动作空间

MG 动作设置为恒温控制负荷对应的4 个优先级动作，价格响应负荷对应的5 个价格水平动作；电量过剩时向主电网售电、电池储能设备存储电量、使用电解槽并向氢气储能设备充氢共3 个动作；电量短缺时向主电网购电、电池储能设备供电、氢气储能设备放氢并使用燃料电池共3 个动作；热量短缺时确定购买天然气、氢气储能设备放氢并使用燃气锅炉共2 个动作。记MG 动作集at={at(0)，at(1)，at(2)，at(3)，at(4)}。具体地，务个动作的物理含义见附录B。

3）奖励

为获得最优经济收益，设定MG 能量管理的目标是最大化奖励Rt，其定义为MG 执行相关动作所获收益与所需成本之差。

式中：Rrev为MG 执行动作所获收益；Rcost为MG 执行动作所需成本；ρload为价格响应负荷的电价；ρmarket为市场电价；σ为调整ρb，t的参数；ρTCL为恒温控制负荷的电价；ze，S，t为时刻t向主电网的售电量；ρcost，W为风力发电设备发电的成本价格；ρcost，PV为光伏发电设备发电的成本价格；ρsold，t为时刻t向主电网售电的调控价格，则ρsold，t ze，S，t为时刻t售电的传输成本；ρpurchased，t为时刻t从主电网买电的调控价格；ze，P，t为时刻t从电网购电的电量；ρgas，t为时刻t的天然气价格；Ngas，t为时刻t从外部网络购买的天然气量；Ccarbon，t为时刻t的环境成本，是天然气燃烧产生的CO2排放量和从主电网购电所造成的经济损失。

Ccarbon，t=ρCO2(ΨgasNgas，t+Ψeze，P，t) （24）

式中：Ψgas、Ψe分别为与天然气燃烧、购买的净电力相关的CO2排放率；ρCO2为碳税价格，其将碳排放量转化为经济惩罚。

1.3 多MG 能量管理模型

考虑由N个MG 互相连接组成的多MG 系统，由于每个MG 难以准确预测本地负荷的用电需求，可能造成MG 可再生发电量的过剩或短缺，故MG间允许电量交易以降低供电风险。一般情况下，与相距较远的主电网相比，相互连接的MG 之间物理距离较近，MG 间电量交易的传输成本更低，故设定MG 之间优先进行电量交易，并设计基于可再生能源渗透率的MG 间电量交易机制。定义第i个MG的可再生能源渗透率为pREP，i。

式中：Pi，W，t、Pi，PV，t、Pe，i，t分别为时刻t第i个MG 的风力发电功率、光伏发电功率、总负荷功率。

电量交易过程中，若有多个MG 电量富余，则可再生能源渗透率高的MG 提供能量；若多个MG 能量短缺，则可再生能源渗透率低的MG 获得能量。

设定多MG 交易电价与主电网电价的关系为：

式中：ρP，t、ρP，t分别为在时刻tMG 间电量的卖价、买价。

在电力市场中，传输损耗导致交易成本的高低会影响买价和卖价之间的差额［25］，导致MG 从主电网购买的价格通常高于MG 出售给主电网的价格。由于本地多MG 交易市场中的交易成本可以忽略不计［26］，销售价格被设置为与购买价格相同。本文设置多MG 交易电价在主电网交易电价之间，以鼓励多MG 电量交易［27］。假设所有MG 商定交易价格为ρP2P，t，其计算公式如下：

式中：∂P2P为价格系数。

多MG 系统中每个MG 与主电网连接以允许电量交易，且MG 之间相互连接可进行电量交易，故基于单MG 的MDP 模型构建多MG 能量管理模型。将每个MG 视作一个智能体，智能体观察MG 状态st并选择动作at。若动作at执行电量交易，则MG 将交易信息发送至能量管理平台。能量管理平台收集信息并利用交易规则设计MG 间电量交易策略，然后将交易决策下发至每个MG 以控制务设备的运行，保证多MG 运行的经济收益最大。具体地，定义多MG 能量管理MDP 模型的务元组如下。

1）状态空间

在t时刻的每个MG 状态为st，与单MG 的MDP模型相比，式（28）中增加了MG 间电量交易价格ρP2P，t。

2）动作空间

由于设计的交易机制允许MG 之间优先进行电量交易，故与单MG 相比，动作的改变主要在电量交易方面，即电量过剩时向主电网售电改为优先向其他MG 售电，电量短缺时从主电网购电改为优先从其他MG 购电。

3）奖励

多MG 能量管理的奖励Rtotal，t为所有MG 的奖励值之和。

式中：Ri，t为第i个MG 在时刻t获得的奖励，定义为第i个MG 获得的经济收益。

式中：Ri，cost为第i个MG 执行相关动作所需成本，与式（23）相同；Ri，rev为第i个MG 执行相关动作所获收益。

式中：Ri，P2P，t为第i个MG 在时刻t与其他MG 进行电量交易获得的收益；Pi，load，u，t为第i个MG 中第u个价格响应负荷在时刻t的电力负荷；Pi，TCL，v，t为第i个MG 中第v个恒温控制负荷在时刻t的电力负荷。

式中：zij，e，t为第i个MG 和第j个MG 之间在时刻t的电量交易量。当zij，e≤0时，0-1 变量I|zij，e，t≤0=1、I|zij，e，t＞0=0；当zij，e＞0时，I|zij，e，t＞0=1、I|zij，e，t≤0=0。

2 能量管理策略

针对构建的多MG 能量管理MDP 模型，可采用DRL 算法来设计能量管理策略。为保护数据隐私，通常每个MG 独立进行本地训练。但单MG 的数据多样性有限，训练过程中智能体易陷入局部最优。为提高MG 智能体的泛化性并保障数据安全，本文把FL 引入多MG 来设计Dueling DQN 能量管理策略，同时利用SCA 降低FL 的通信时延。

2.1 Dueling DQN 算法

Dueling DQN 是针对传统DQN 执行动作所得Q值存在高估，可能陷入局部最优而影响算法的稳定性的局限而提出的算法，其通过优化神经网络（neural network，NN）结构，即将NN 的输出Q值分为独立的状态值和动作值来提高算法鲁棒性［28-29］。Dueling DQN 的输出包括两部分：其一为仅与状态有关而与选取动作无关的价值函数，记为V(s；θ，β)；其二为与状态和动作均有关的优势函数，记为A(s，a；θ，α)。最终得到的Q网络输出如下。

式中：s为状态值；θ为公共部分的网络参数；β为价值函数的网络参数；α为优势函数的网络参数。

若直接用式（33）更新Q值，存在不可辨识性问题。为提高函数可辨识度与算法稳定性，Dueling DQN 对优势函数进行了去中心化处理。

式中：a′为下一时刻的动作；1/|A|为优势函数的平均值。

Dueling DQN 训练过程中，从经验池中随机抽取训练样本(sm，am，rm，)来计算目标Q值，其中，经验池的形成过程见附录C，目标Q值ym的计算式为：

Dueling DQN 中，定义损失函数L为目标Q值与预测Q值的均方差。

通过迭代更新神经网络参数来最小化损失函数而得到最优模型。

2.2 联邦Dueling DQN 算法

FL 是一种在保护数据安全的前提下解决数据孤岛问题的分布式机器学习技术，其原理为：多个参与方先利用本地私有数据训练模型，并把务自的模型权重参数上传至服务器端进行聚合后，下发更新的全局模型至务参与方［30］。基于此，本文结合FL与Dueling DQN 算法提出联邦Dueling DQN，见附录D 表D1，其工作流程如附录D 图D1 所示。

步骤1：创建初始模型并发送至每个客户端；

步骤2：务个客户端利用私有数据和Dueling DQN 算法训练本地模型；

步骤3：客户端将模型权重参数ωi上传至中心服务器；

步骤4：中心服务器聚合所有客户端的模型得到全局模型ωG；

步骤5：把更新的全局模型反馈给客户端。

重复步骤2 至5，直到达到FL 的最大迭代次数。联邦Dueling DQN 的模型聚合可采用联邦平均算法（federated averaging algorithm，FedAvg），其对务个客户端的梯度更新进行平均而形成全局模型且实现简单。

2.3 基于SCA 的联邦Dueling DQN 能量管理策略

联邦Dueling DQN 算法中，为训练出性能较优的全局模型，本地MG 与中心服务器之间需要频繁交互模型参数，耗费大量时间与通信资源。为解决此问题，本文将SCA［31］应用于联邦Dueling DQN 学习算法中，设计基于SCA 的联邦Dueling DQN 能量管理策略，利用评分代替FedAvg 中客户端的模型权重，减少数据交互量而降低了通信时延。

SCA 是一种利用正弦和余弦函数的数学特性对优化问题求解的算法。作为一种群体智能优化算法，其运行时创建多个初始随机候选解，然后利用下式进行个体更新：

式中：XXiitrd为第d维第iitr次迭代的当前解；XBiitrd为第d维第iitr次迭代的最优解；Miitr为SCA 迭代的最大次数，即本地MG 与中心服务器交互次数；k2为［0，2π］之间的随机数；k3为［0，2］之间的随机数；k1为控制参数。

SCA 使随机候选解基于正弦和余弦的数学模型向最优解的方向波动，利用多个随机变量和自适应变量来计算当前解所在位置，从而可以搜索空间中的不同区域，有效避免局部最优而收敛于全局最优。

根据SCA 计算模型参数值如下式所示。

基于SCA 的联邦Dueling DQN 设计的多MG能量管理策略如附录D 表D2 所示，其工作流程如图2 所示。

基于SCA 的联邦Dueling DQN 能量管理策略流程的具体步骤如下：

步骤1：创建初始模型并发送至每个MG；

步骤2：务个MG 利用私有数据和Dueling DQN算法训练本地模型；

步骤3：MG 计算模型更新完成后的损失函数值，并将其将作为评分标准发送至中心服务器；

步骤4：中心服务器比较所有MG 的评分，选取最优评分所对应MG 的ID，记为XB，id；

步骤5：中心服务器向ID 号为XB，id的MG 发送请求；

步骤6：接收到请求的MG 将本地模型上传至中心服务器；

步骤7：中心服务器更新全局模型XBωiitrd；

步骤8：服务器将更新的全局模型XBωiitrd反馈至MG；

步骤9：每个MG 利用SCA 和全局模型更新本地模型。

重复步骤2 至9，直到达到最大迭代次数，使得算法收敛，最终得到MG 能量管理的最优决策。进一步，依据文献［32］对FL 算法进行性能分析，附录E 给出了该算法的收敛性证明。

所提能量管理策略利用SCA 更新本地模型参数，每个MG 无须上传全部模型参数，只需上传损失函数值作为评分标准。同时，具有最优评分的MG上传其模型参数至能量管理平台的中心服务器，以更新全局模型，大幅减少从本地MG 传输至中心服务器的数据量。实际工况运行过程中，所提多MG能量管理策略的实现分为离线和在线2 个阶段。在离线阶段，基于务MG 存储的历史数据信息，利用SCA 的联邦Dueling DQN 对智能体进行训练，并保存训练完成的模型，供在线阶段调用。MG 在线运行时，智能体实时观测MG 的状态，结合状态信息和训练模型输出能量管理策略，MG 据此策略执行相应动作，同时，将更新的状态与奖励值存储至离线数据库，供后续训练。在线阶段可直接调用离线训练模型，保证多MG 能量管理的实时调控要求。

3 仿真实验与结果

3.1 环境设置

不失一般性，本文采用3 个MG 构成如图1 所示多MG 系统，其相关参数如表1 所示。

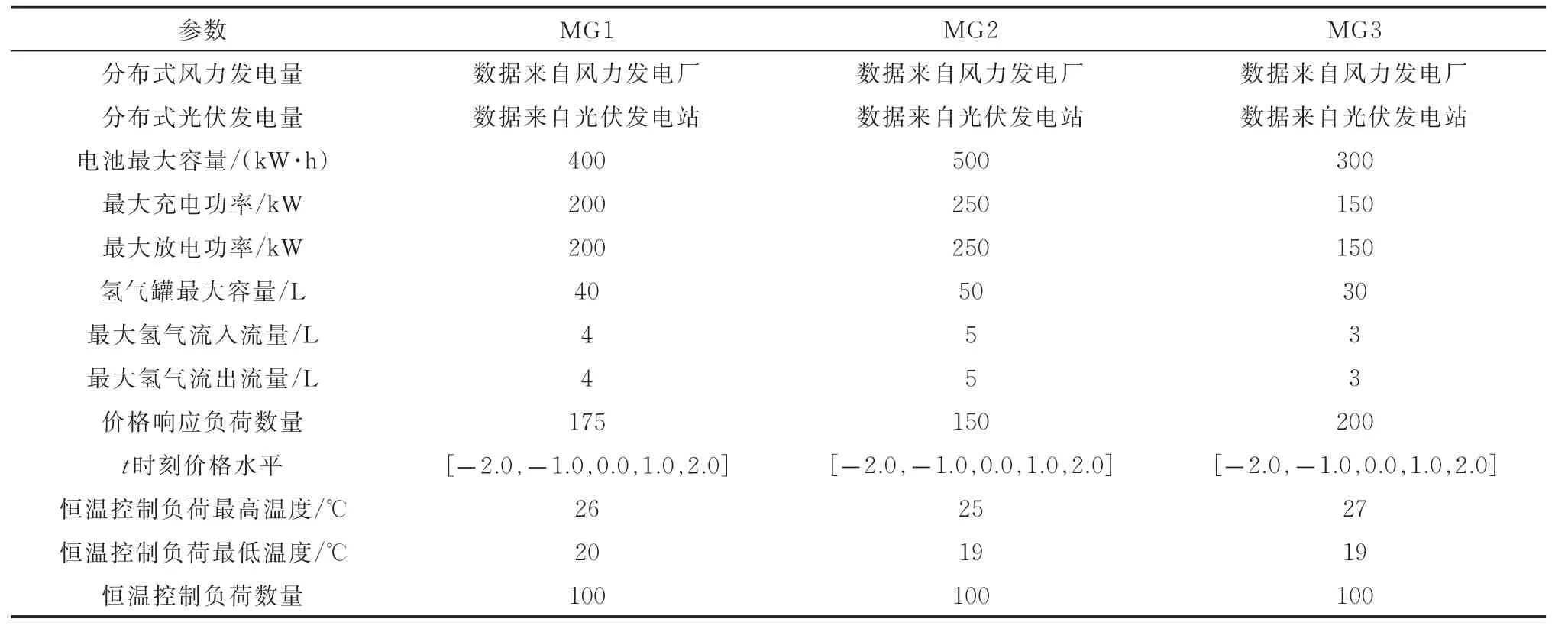
表1 MG 系统参数Table 1 Parameters of MG system

每个MG 采用文献［33-34］提供的风力发电数据、光伏发电数据和电力负荷数据。MG 中能量转换装置参数如表2 所示。

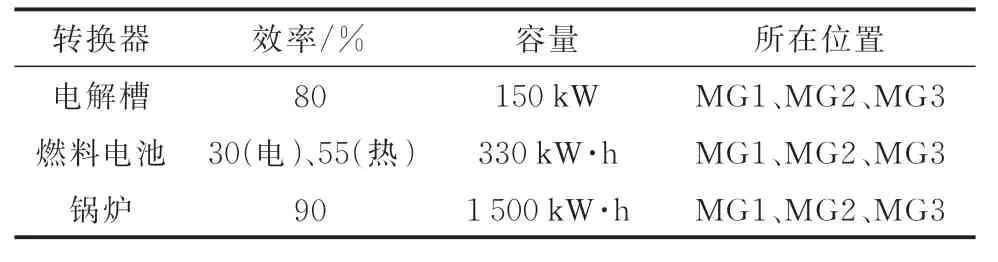
表2 能量转换装置参数Table 2 Parameters of energy conversion devices

设定风力发电成本为32 欧元/(MW · h)、光伏发电成本为42 欧元/(MW · h)、市场电价为 5.48 欧元 / (MW·h)、天然气价格为0.13 欧元/(MW·h)、碳税价格为0.02 欧元/kg。采用卷积神经网络以10 d 的数据为总样本进行训练，一个训练回合对应1 d，时间间隔1 h。仿真软件采用Python 3.6.1 和Tensorflow 1.8.0。

3.2 结果分析

基于构建的多MG 仿真环境，通过智能体训练过程中总奖励值来比较不同算法的性能。首先，对比了分别采用Dueling DQN 和联邦Dueling DQN 算法的能量管理策略获得的奖励值，如附录F 图F1 所示。Dueling DQN 算法部署在每个本地MG，由每个MG 进行本地独立训练，与联邦Dueling DQN 均属于分布式能量管理方式。为直观展示，图F1 中对奖励值进行了归一化。可以看到，采用联邦Dueling DQN 获得的奖励值高于一般Dueling DQN，且算法的收敛性更优，同时表明Dueling DQN 中引入FL 能够提升能量管理性能，这主要因其利用了多个MG 的模型参数构成一个更泛化的全局模型。

图3 给出了基于SCA 的联邦Dueling DQN、联邦Dueling DQN 和文献［12］采用的联邦DQN的能量管理策略的奖励值。可以看出，所提基于SCA 的联邦Dueling DQN 可得到更高奖励值且收敛性更优，增加了MG 的经济收益。这主要由于：1）Dueling DQN 是原DQN 算法的改进，解决了DQN 的过估计问题，其与FL 结合后仍具优势；2）本文引入SCA 进一步改进了联邦Dueling DQN，故总体性能优于联邦Dueling DQN 和联邦DQN。

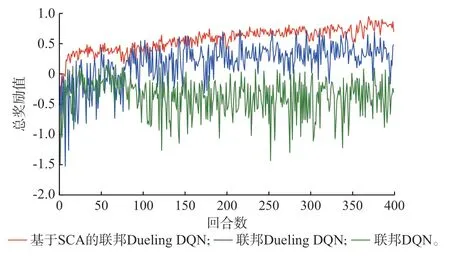
图3 采用不同能量管理策略下的奖励值对比Fig.3 Comparison of rewards by different energy management strategies

为了分析SCA 对模型训练过程中参数传输时延的影响，采用联邦Dueling DQN 算法与基于SCA的联邦Dueling DQN 进行一次全局模型更新的通信时延对比。仿真中假设信道的信噪比SNR 为30 dB，图4 给出了不同信道传输带宽时模型参数的传输时延对比。可以看出，改进的联邦Dueling DQN 的通信时延降低了50%以上，这主要是因为SCA 减小了数据传输量。

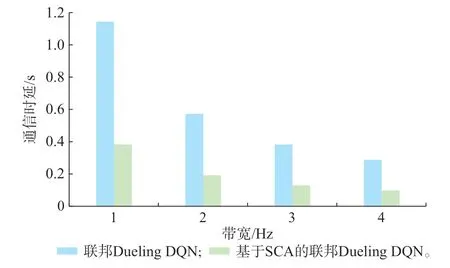
图4 通信时延对比Fig.4 Comparison of communication latency

上述性能对比结果表明，所提基于SCA 的联邦Dueling DQN 能量管理策略具有明显性能优势。利用该策略进行仿真计算可得，MG 仅与主电网交易时，10 d 总收益为-836 欧元，而采用本文所提电量交易机制的MG，10 d 总收益为140 欧元，即优先进行MG 间交易可以提高多MG 系统的经济收益。

同时，MG 仅允许与主电网交易和优先进行MG 间交易两种方式下，连续10 d 的每日经济收益对比如附录F 图F2 所示。可以看出，多MG 能量管理过程中，采用所提电量交易机制获得的每日收益更高。

以1 d 为例，分析务MG 采用所提计及能量交易与转换的管理策略的能量管理结果。

1）对于MG1，经基于SCA 的联邦Dueling DQN策略调节后，MG1 中恒温控制负荷与价格响应负荷的每小时用电功率见附录F 图F3，发电设备的发电功率与用电负荷的用电总功率如附录F 图F4 所示。可以看出，MG1 在24 h 中发电功率较少，发电功率只在09：00—14：00 时满足用电功率。其与主电网、其他MG 进行电量交易的销售价格和购买价格如附录F 图F5 所示。一般情况下，当发电功率低于用电功率时，MG1 从其他MG 购电，若仍不满足则从主电网购电；在发电功率高于用电功率时，MG1 向其他MG 售电以最大化收益，并在售电后有剩余电量时向主电网售电。但在实际情况中，MG1 与主电网和其他MG 的交易量如附录F 图F6 所示，MG1在09：00—14：00 时直接向主电网售电，在17：00、18：00 时刻直接从主电网购电。结合MG2、MG3 发电功率与用电负荷的用电总功率，MG1、MG2、MG3 在09：00—14：00 时均处于发电功率满足用电功率的状态；MG1、MG2 在07：00、18：00 时刻处于发电功率低于用电功率的状态；MG3 在07：00、18：00 时刻发电功率正好满足用电功率，这些时刻MG 间发生交易冲突，所以MG1 直接与主电网进行电量交易。MG1 的每小时热负荷需求量如附录F图F7 所示。由于MG1 以与其他MG 和主电网进行电量交易为主，未将多余电量转换为氢气存储，故其热负荷需求以购买天然气并由燃气锅炉转化为热量为主。

2）对于MG2，经基于SCA 的联邦Dueling DQN策略调节后，MG2 中恒温控制负荷与价格响应负荷每小时用电功率如附录F 图F8 所示，发电设备的发电功率与用电负荷的用电总功率如附录F 图F9 所示。可以看出，MG2 在1 d 中发电设备发电功率较多，在00：00—15：00 时发电功率满足用电功率，MG2 与主电网和其他微网的交易量如附录F 图F10所示，在00：00—08：00 时向MG1 出售电量，若电量仍有剩余，则向主电网出售电量。由于发生交易冲突，在09：00—14：00 时MG2 直接向主电网出售电量，在17：00、18：00 时刻MG2 直接从主电网购买电量。在16：00、19：00—23：00 时，MG1 和MG2 均处于发电功率低于用电功率的状态，但MG2 的可再生能源渗透率高于MG1，故MG2 直接从主电网购电。MG2 每小时热负荷需求量如附录F 图F11 所示。由于MG2 以与MG1 和主电网进行电量交易为主，而未将多余电量转换为氢气存储，故其热负荷需求以购买天然气并由燃气锅炉转化为热量为主。

3）对于MG3，经基于SCA 的联邦Dueling DQN策略调节后，MG3 中恒温控制负荷与价格响应负荷每小时用电功率如附录F 图F12 所示，发电设备的发电功率与用电负荷的用电总功率如附录F 图F13所示。可以看出，MG3 在24 h 中发电功率较多，仅在00：00—08：00 时发电功率低于用电功率。MG3与主电网和其他MG 的交易量如附录F 图F14 所示，由于MG1 的可再生能源渗透率比MG2 低，故MG3 选择与MG1 进行电量交易，若电量还有剩余，则MG3 将电量出售至主电网。MG3 的每小时热负荷需求量如附录F 图F15 所示。由于MG3 主要与MG1 和主电网进行电量交易，而未将多余电量转换为氢气存储，故其热负荷需求主要为购买天然气并由燃气锅炉转化为热量。

通过仿真结果观察到，MG 以与其他MG 或主电网进行电量交易为主，每个MG 未选择使用储氢罐，从而其热负荷需求由从外部网络购买天然气提供，故CO2排放量增多。进一步分析不同碳税价格对多MG 收益与CO2排放量的影响，如附录F 图F16 所示。当碳税价格从0 增长到0.01 欧元/kg 时，每个MG 主要与主电网进行电量交易，导致CO2排放量增加；当碳税价格从0.02 欧元/kg 增长到0.04 欧元/kg 时，CO2排放量逐步减少。随着碳税价格的增长，收益呈现出不同程度的上升，这是因为随着碳税价格的上涨，多MG 采用了更环保的能量管理策略，即通过使用氢气这一清洁能源减少CO2排放量。