电网故障下含直驱风电机组的电力系统频率动态响应分析

欧阳金鑫，余建峰，张澳归，皇甫百香，姚 骏

（重庆大学电气工程学院，重庆市 400044）

0 引言

为应对能源危机，新能源渗透率不断提高。大规模新能源并网降低了电力系统的惯量水平，系统抗扰能力持续下降［1-2］。直驱风电机组（direct-drive wind turbine，DDWT）是风力发电的主流机型之一，具有可控性高、运行效率高、维护成本低等优点［3-4］。DDWT 具有不同于同步机的运行原理和控制特性，特别是DDWT 具有快速可控的功率响应，使得电网故障下的系统动态特性变得十分复杂。电网发生短路故障时，机端电压跌落使DDWT 输出有功功率变化，可能导致系统功率不平衡。故障切除使负荷或电源退出，电压恢复和控制策略调整使得DDWT 功率变化，加剧了系统功率不平衡，可能引起电力系统暂态频率失稳。随着DDWT 的大量应用，风电系统的安全稳定运行面临着严峻挑战［5］。

DDWT 可利用转子存储的旋转动能和直流电容存储的电能来参与电力系统频率控制。电力系统发生功率扰动后，频率变化轨迹或最大频率偏差等特征量的量化可为DDWT 及其并网系统的频率控制提供依据。现有电力系统频率特性分析主要包括时 域 仿 真 法［6-7］、模 型 解 析 法［8-9］和 人 工 智 能 方法［10-11］。时域仿真法通过建立详细的设备全状态动态模型，采用数值求解微分代数方程组，分析系统务节点频率的时空分布特性。时域仿真法具有建模精确、结果直观的特点，但新能源与电力电子设备占比的提高加剧了建模难度，模型求解速度与精度常常难以兼顾。

模型解析法主要包括系统频率模型和系统频率响 应 模 型（system frequency response model，SFRM）。文献［12］建立了新能源接入电网的通用平均系统频率模型，在保证准确度的同时降低了模型阶数，但主要关注同步机的低阶建模。文献［13］提出了计及风电功率波动的改进SFRM；文献［14］考虑风电场风速差异性，构建了含多台风电等值机组的扩展SFRM。但是，上述研究忽略了电网扰动下电压变化对系统频率特性的影响。随着风电系统复杂程度的不断提高，以数据驱动为代表的人工智能方法逐步获得关注［15］。文献［16］提出一种计及频率偏移分布与惩罚代价的最大频率偏移预测方法。文献［17］提出一种基于SFRM 与极限学习机的频率在线预测方法。人工智能方法从数据角度揭示了系统频率特性，但其脱离了物理机理，难以为频率控制提供指导，而且训练和实现依赖于大量样本数据。

模型解析法具有计算简单、物理过程清晰的特点，但现有方法主要针对负荷突变场景，尚未计及电网故障下DDWT 暂态响应对系统频率的影响。综合 惯 量 控 制（synthetic inertia control，SIC）使 得DDWT 功率与系统频率耦合。DDWT 的功率控制依赖于锁相环（phase-locked loop，PLL）实时跟踪并网点电压相角。电网故障发生及切除瞬间，DDWT并网点电压相角突变引发锁相暂态响应，可能导致锁相偏差［18］。锁相偏差通过变流器控制传导改变DDWT 频率响应特性，可能给电力系统频率特性分析带来误差。为此，提出了电网故障下DDWT 锁相偏差的量化方法；分析了锁相偏差的传导路径，提出了锁相暂态响应引起功率控制误差的计算方法；建立了含DDWT 的SFRM，提出了锁相暂态影响下系统频率变化率和最大频率偏差的计算方法，解析了电网故障下的系统暂态频率响应特性，可为电网故障下电力系统频率安全评估和紧急控制提供参考。

1 DDWT 锁相暂态响应特性

DDWT 由风力机、永磁同步发电机、背靠背变流器以及控制系统组成。风力机将捕获的风能转化为机械能，驱动同轴连接的永磁同步发电机旋转，从而产生电能。控制系统主要包括桨距角控制、机侧变流器（machine-side converter，MSC）和网侧变流器（grid-side converter，GSC）控制。变流器通常采用双闭环矢量控制［19］。MSC 采用零d轴电流控制实现有功功率控制，定子d、q轴电压参考值、为：

式中：Gmi、Gmo分别为MSC 的内环和外环比例-积分（proportional-integral，PI）控制器传递函数；isd、isq分别为定子d、q轴电流；为定子d轴电流参考值；Pw、分别为有功功率的实时值和参考值；Ld、Lq分别为发电机定子d、q轴电感；ωe为发电机电角速度；ψf为发电机永磁体的磁链幅值。

GSC 采用电压定向矢量控制实现直流电压和无功功率的解耦控制，网侧d、q轴电压参考值、可写为：

式 中：Ggi、Ggo分 别 为GSC 的 内 环 和 外 环PI 控 制 器传递函数；ugd、ugq分别为并网点d、q轴电压；igd、igq分别为网侧d、q轴电流；ωs为电网同步角速度；Ls为滤波电感；Udc、U分别为直流电压的实时值和参考值；Qw、分别为无功功率的实时值和参考值。

电网正常运行时，DDWT 运行于最大功率点跟踪（maximum power point tracking，MPPT）模 式。当电网频率偏差大于DDWT 调频死区时，SIC 启动并引入补偿功率PSIC，经限幅环节输出至MSC 以调整DDWT 的有功功率输出。DDWT 的SIC 如图1所示。图中：Pmppt为MPPT 控制下DDWT 的有功功率。

补偿功率可写为：

式中：Δf为频率偏差；kd、kp分别为下垂和惯量系数。

MSC 和GSC 的控制依赖于PLL 确定的同步旋转坐标系。PLL 的输入为DDWT 的并网点电压，通过同步坐标变换将输入电压变换为d、q轴电压，q轴电压经滤波器和积分控制输出相角，从而跟踪并网点电压的实际相角［20］。电网发生故障后，DDWT 并网点电压幅值跌落，相位发生跳变。此时，PLL 输出相角的频域表达为：

电网发生故障时，并网点电压相角突变，PLL输出相角难以迅速跟踪电压的实际相角，从而产生锁相偏差。对式（4）进行Laplace 逆变换，可得锁相偏差的时域表达为：

式中：θac为并网点电压实际相角；参数ξ、ωn、ωl和φ分别为

电网故障后，并网点电压相角跳变引发锁相暂态响应，产生了正弦衰减的锁相偏差。锁相偏差的衰减速度取决于并网点电压幅值和PI 控制器比例系数。PI 控制器比例系数通常为定值，故电压跌落程度越大，锁相偏差的衰减速度越慢。最大锁相偏差取决于并网点电压的初相角和相角突变量。故障切除瞬间，并网点电压相角再次突变，又将产生锁相偏差。电网故障后，锁相暂态响应对DDWT 的输出特性产生直接的影响。

2 电网故障下DDWT 频率响应特性

锁相偏差对DDWT 频率响应特性影响的路径如图2 所示。图中：Δ、Δ分别为锁相偏差在电流内环中产生的电流和电压偏差；Δ为锁相偏差在三相调制电压生成过程中产生的电压偏差；PWM 表示脉宽调制。GSC 外环控制的直流电压和无功功率参考值与实时值的偏差经PI 控制器产生d、q轴电流参考值；电流内环控制将d、q轴电流参考值与实时值的偏差输入PI 控制器，叠加并网点d、q轴电压后产生网侧d、q轴电压参考值，从而分别控制直流电压和无功功率。锁相偏差通过派克变换在并网点d、q轴电压变换过程引入，导致DDWT 输出有功功率与功率参考值出现第1 次误差。网侧d、q轴电压参考值通过派克逆变换产生三相电压调制信号，用以触发GSC 实施控制。锁相偏差通过派克逆变换在三相电压调制信号生成过程中引入，导致第2 次功率控制误差。

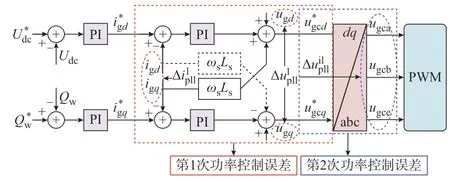
图2 锁相偏差传导路径Fig.2 Conduction paths of phase-locked deviation

2.1 第1 次功率控制误差解析

根据派克变换原则，DDWT 并网点d、q轴电压可表示为［21］：

频率响应的时间尺度通常为秒级以上，而电流内环控制响应时间为毫秒级。因此，可认为网侧电流实时值与参考值相等［22］。DDWT 输出有功功率可写为：

根据式（8），可得锁相暂态响应影响下DDWT的第1 次功率控制误差为：

由式（9）可知，第1 次功率控制误差主要受并网点电压幅值和锁相偏差的影响。当并网点电压一定时，随着锁相偏差的增大，第1 次功率控制误差呈现出先减小后增大的趋势。当锁相偏差一定时，并网点电压跌落程度越大，则第1 次功率控制误差越小。

2.2 第2 次功率控制误差解析

电网故障下，GSC 的三相调制电压可写为：

以a 相为例，联立式（5）和式（10），可得GSC 的a 相调制电压为：

式中：U为GSC 交流电压参考值的幅值；ωp1、ωp2、α0和α1分别满足

基于滤波回路可求解DDWT 的输出有功功率，得到第2 次功率控制误差为：

式中：Rs为滤波电阻；T为工频周期；参数Ap和Bp的具体表达式见附录A。

第2 次功率控制误差主要受到并网点电压幅值和锁相偏差的影响。当并网点电压一定时，随着锁相偏差的增大，GSC 调制电压非工频分量逐渐增大，导致第2 次功率控制误差逐渐增大。因此，随着锁相偏差的增大，2 次功率控制误差可能逐渐增大，导致DDWT 输出的有功功率增大，锁相暂态响应导致的功率控制误差显著影响DDWT 的频率响应特性。

联立式（3）、式（9）和式（13），2 次功率控制误差影响下DDWT 的频率响应特性可表示为：

式中：vr为故障切除后DDWT 的功率恢复速度；tfr为故障切除时刻。

3 含DDWT 的系统频率动态响应分析

电力系统频率特性分析是系统受到功率扰动后，对系统频率和扰动功率的响应关系与未来一段时间内系统频率动态特性的解析［23］。功率扰动是指电源出力与负荷之间的不平衡功率。电网故障下的功率扰动主要包括2 个部分：故障期间电源出力变化与故障过渡电阻消耗的功率；故障切除导致元件退出造成的不平衡功率。电网故障导致系统出现功率不平衡后，同步机通过调速系统改变转子旋转动能响应系统频率变化；风电场通过综合惯量控制抵御系统频率变化。

在DDWT 综合惯量控制和锁相暂态响应的基础上，建立计及功率控制误差的改进SFRM，如图3所示。图中：Pmax、Pmin分别为DDWT 的有功功率最大和最小约束；SG 表示同步机。

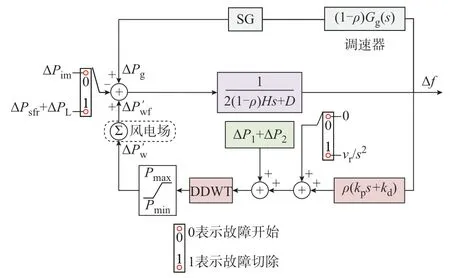
图3 电网故障下的SFRMFig.3 SFRM under power grid fault

风电机组的功率-转速非线性关系和变流器控制非线性环节是SFRM 误差的主要来源［24］。风电机组功率-转速关系的线性化拟合误差较小，其影响可以忽略［25］。变流器控制非线性环节主要包括PI控制器和变流器限幅环节。频率响应时间尺度内，可忽略PI 控制器的暂态过程影响。当系统频率偏差过大导致DDWT 的有功功率输出受限时，DDWT 的频率响应输出为恒定值。

同步机和风电场的功率变化量与不平衡功率之差驱动系统惯性和阻尼响应，从而改变系统频率特性。电网故障下系统频率特性可表示为：

式中：ρ为DDWT 渗透率；H为系统惯性时间常数；D为系统负荷阻尼常数；ΔPg为同步机的功率变化量；ΔP′wf为直驱风电场的功率变化量；ΔPim为故障瞬间的系统不平衡功率；ΔPsfr为故障切除瞬间的电源功率变化量；ΔPL为故障切除导致的负荷功率变化量。

利用机端频率变化率可估算故障瞬间的不平衡功率［17］：

式 中：fN为 额 定 频 率；Hi为 第i台DDWT 的 惯 性 时间常数；fi为 第i台DDWT 的测量频 率。

当系统频率偏差大于同步机调频死区时，同步机调速系统动作改变汽轮机调节汽门，高温蒸汽进入高压汽室膨胀做功，高压汽室的排汽通过再热器重新加热，再进入中压和低压汽室进一步膨胀做功。由于高压汽室和低压连通管的时间尺度远小于再热器，同步机的频率响应可忽略高压汽室和低压连通管的反应过程［26］。同步机的功率变化量为：

同步机调速系统的传递函数Gg(s)为：

式中：RD为同步机调速器下垂系数；TR为再热器时间常数；FH为高压汽室发电比例；Km为同步机机械功率增益。

当频率偏差大于DDWT 调频死区时，综合惯量控制引入补偿功率。根据式（14），考虑锁相暂态响应导致的2 次功率控制误差，直驱风电场的功率变化量可表示为：

式中：nw为电网故障切除后DDWT 的数量；vr，i为故障 切 除 后 第i台DDWT 的 功 率 恢 复 速 度；ΔP1，i、ΔP2，i分 别 为 第i台DDWT 的 第1 次、第2 次 功 率 控制误差。

联立式（15）、式（17）和式（19），可得电网故障下系统频率偏差的频域表达式为：

其中，参数a1、b1、c1、w1、w′1、w2、w3、M和N满足：

式中：θ0，i为电网故障前第i台DDWT 的并网点电压初 相 角；Δθ0，i为 第i台DDWT 的 电 压 相 角 突 变 量；Ugf，i为 第i台DDWT 的 并 网 点 电 压 幅 值；，i、，i分别为第i台DDWT 的网侧d、q轴电流参考值。

对式（20）进行Laplace 逆变换，可得电网故障下风电电力系统频率偏差的时域表达式为：

式中：故障切除后非指数项中t-tfr不能超过(Pg0-Pgf0)/vr，其 中，Pg0为DDWT 正 常 运 行 时 的 初 始 功率，Pgf0为故障期间DDWT 的有功功率。由于系统频率不能跳变，故障切除瞬间的频率偏差应保持不变，进而可求解故障切除瞬间的电源功率变化量（见附录A）。

特征根s1、s2、s3、s4、s5、s6、s7分别满足：

由式（22）可知，锁相暂态响应改变了电网故障下的系统暂态频率特性，系统频率包含稳态分量和衰减分量。锁相暂态响应通过影响GSC 电流内环控制和变流器调制电压生成过程，增大了电网故障下的频率稳态分量。由于锁相偏差的影响，电网故障下暂态频率偏差更大。系统频率衰减分量呈现出衰减振荡的特征，衰减速度取决于故障电压幅值和DDWT 渗透率。对式（22）求导，可得电网故障下的频率变化率为：

由式（24）可知，电网故障切除后，负荷退出产生不平衡功率，可能导致系统频率变化率发生突变。电网故障持续时间通常在100 ms 以内，电网故障切除导致系统不平衡功率变化。因此，系统最大频率偏差出现在故障切除后。利用式（24）可求解暂态频率处于极值的时间texm，将极值时间texm代入式（22）后，可求解得系统最大频率偏差Δfm为：

由式（25）可知，系统最大频率偏差受到DDWT渗透率、故障后并网点电压幅值和电压相角突变量的影响。电网故障导致并网点电压相角突变，电压相角突变量通过锁相暂态响应改变系统最大频率偏差。通过实时测量电网故障下的电压幅值和电压相角突变量，结合同步机和DDWT 的控制参数，利用式（24）即可实现电网故障下系统频率变化率的动态响应分析，利用式（25）可实现电网故障下系统最大频率偏差的动态响应分析。

4 算例分析

4.1 等值系统不同风电渗透率下的仿真验证

在MATLAB/Simulink 中搭建如图4 所示的四机两区域等值系统模型。图中：Xg1、Xg2、Xg3分别为同步机出口线路电抗；X1、X2、X3分别为传输线路电抗。同步机SG1、SG2 和SG3 的容量分别为250、250、200 MW，额定频率为50 Hz。直驱风电场由若干台DDWT 组成。单台DDWT 的额定容量为2 MW，额定电压为690 V，定子电阻为0.02 p.u.，定子d、q轴电感分别为0.51 p.u.和0.51 p.u.，直流电容为20 mF，永磁体磁链为1.776 Wb，极对数为48。SFRM 等值参数见附录B。

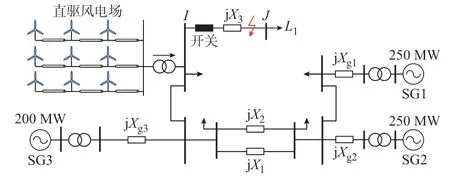
图4 四机两区域等值系统Fig.4 Four-machine two-area equivalent system

本文采用的低电压穿越控制策略为：电网故障期间，直驱风电场无功功率控制参考值根据电网导则GB/T 36995—2018 确定［27］，并按照容量分配给每台DDWT。通过比较不同风电渗透率下本文所提方法、忽略锁相暂态的方法的频率变化率/偏差计算结果和系统实际频率变化率/偏差之间的误差，验证本文所提方法的有效性。其中，本文所提方法以式（16）和故障切除导致退出运行的负荷功率为输入，代入式（24）计算系统频率变化率，代入式（25）计算系统最大频率偏差。忽略锁相暂态的方法未考虑式（19）中的2 次功率控制误差。

系统总负荷为1 350 MW，负荷L1为系统总负荷的20%。t=60 s 时，线路IJ在距离直驱风电场升压变压器高压侧母线5 km 处发生三相短路故障，故障后0.2 s 由线路IJ保护动作切除。直驱风电场母线电压、系统频率变化率/偏差和直驱风电场补偿功率如图5 所示。

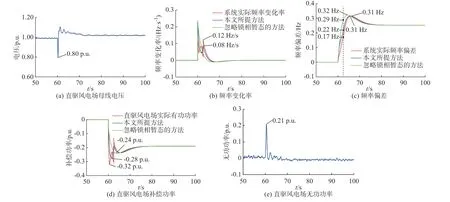
图5 等值系统风电渗透率为50%下的电气量Fig.5 Electrical quantities at wind power penetration rate of 50% in equivalent system

如图5（a）所示，故障期间直驱风电场母线电压跌落至0.80 p.u.，并网点电压相角突变量为25°。由于电压跌落程度较低，故障期间DDWT 有功功率输出不受限。由图5（b）和（c）可见，锁相暂态响应导致系统频率变化率在恢复过程中发生波动，本文所提方法计算的频率变化率和系统实际频率变化率的轨迹基本一致，而忽略锁相暂态响应计算的频率变化率的误差较大。电网故障切除后2.3 s，本文所提方法计算的系统频率偏差的误差为0.05 Hz，而忽略锁相暂态响应时计算的系统频率偏差误差为0.12 Hz。可见，本文所提方法的频率偏差计算结果与系统实际频率偏差基本一致。根据式（25）求解系统最大频率偏差为0.31 Hz，忽略锁相暂态响应计算的系统最大频率偏差为0.32 Hz。这是因为系统最大频率偏差主要取决于系统频率稳态分量，故2 种方法的计算结果差别较小。同时，由于惯性时间常数较大，系统抵御不平衡功率的能力较强，算例分析中的最大频率偏差较小。通过解析锁相暂态响应引起的2 次功率控制误差，本文所提方法可实现电网故障下系统暂态频率特性的准确分析。

电网故障切除导致负荷退出，系统频率升高，直驱风电场通过降低有功功率以抑制频率升高，如图5（d）所示。仿真可得直驱风电场实际补偿功率最大为-0.32 p.u.，根据式（19）计算得到直驱风电场补偿功率最大为-0.28 p.u.。忽略锁相暂态响应时，可得直驱风电场补偿功率最大为-0.24 p.u.，计算误差达到25%。故障期间，直驱风电场提供0.21 p.u.的无功功率支撑，如图5（e）所示。由式（9）和式（13）计算得到的直驱风电场功率控制误差如图6 所示。由图6（a）和（b）可知，第1 次功率控制误差最大为0.10 p.u.，第2 次 功 率 控 制 误 差 最 大 为0.19 p.u.。

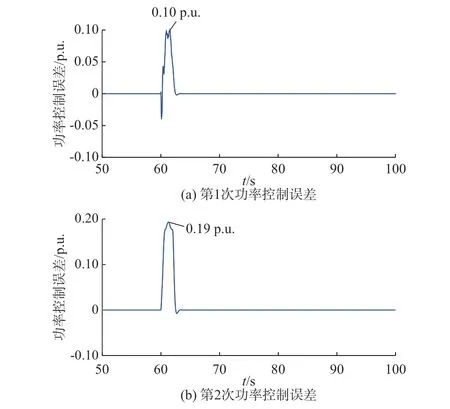
图6 等值系统风电渗透率为50%下的功率控制误差Fig.6 Power control error at wind power penetration rate of 50% in equivalent system

改变风电渗透率至60%，系统总负荷为1 750 MW，负荷L1为系统总负荷的20%。t=60 s时，线路IJ在距离直驱风电场升压变压器高压侧母线5 km 处发生三相短路故障，故障0.2 s 后清除。直驱风电场母线电压、系统频率变化率/偏差和直驱风电场补偿功率如附录C 图C1 所示。由图C1（a）可知，电网故障期间的直驱风电场母线电压跌落至0.81 p.u.，并网点电压相角突变量为30°。故障期间，直驱风电场提供0.17 p.u.的无功功率支撑。本文所提方法计算的频率变化率和系统实际频率变化率的轨迹基本一致，如图C1（b）所示。由图C1（c）可知，t=62.25 s 时，系统实际频率偏差为0.32 Hz，本文所提方法计算的系统频率偏差为0.27 Hz，而忽略锁相暂态响应计算的系统频率偏差为0.46 Hz，误差较大。同时，2 种方法下的系统最大频率偏差计算结果差别较小。如图C1（d）所示，由仿真可知，直驱风电场实际有功出力降低0.43 p.u.，本文所提方法下直驱风电场有功出力降低0.45 p.u.，补偿功率计算误差不超过5%。当忽略锁相暂态响应引起的功率控制误差时，直驱风电场补偿功率为-0.36 p.u.，误差超过16%。锁相暂态响应引起的功率控制误差计算结果如附录C 图C2 所示，其中，第1 次功率控制误差最大为0.15 p.u.，第2 次功率控制误差最大为0.19 p.u.。上述算例结果表明，本文所提方法能够准确分析不同风电渗透率下的系统暂态频率响应特性。

改变风电渗透率为50%，系统总负荷为1 350 MW，负荷L1为系统总负荷的20%。t=60 s时，线路IJ发生三相短路故障，故障后0.2 s 由线路IJ保护动作切除。直驱风电场母线电压、系统频率变化率/偏差、直驱风电场补偿功率、无功和有功功率输出如附录D 图D1 所示。由图D1 可知，电网故障期间的直驱风电场母线电压跌落至0.75 p.u.，并网点电压相角突变量为22°。故障期间，直驱风电场发出0.30 p.u.的无功功率支撑电网电压，由于变流器容量限制导致DDWT 有功功率输出受限，故障期间的DDWT 有功功率降至0.76 p.u.。本文所提方法计算的频率变化率和系统实际频率变化率基本一致。t=63 s 时，系统实际频率偏差为0.21 Hz，本文所提方法计算的系统频率偏差为0.24 Hz，而忽略锁相暂态响应预计算的系统频率偏差为0.31 Hz，误差较大。故障切除导致系统频率升高，直驱风电场实际有功出力降低0.31 p.u.，本文所提方法下直驱风电场有功出力降低0.30 p.u.，而忽略锁相暂态响应时直驱风电场补偿功率为-0.24 p.u.。可见，本文所提方法下补偿功率计算误差不超过3%。锁相暂态响应引起的功率控制误差计算结果如附录D 图D2所示。由图D2 可见，第1 次功率控制误差最大为0.15 p.u.，第2 次功率控制误差最大为0.25 p.u.。

4.2 IEEE 39 节点系统不同负荷切除率下的仿真验证

IEEE 39 节点系统共包含10 台机组，其中，G2、G7 和G8 采用等容量的直驱风电场替代，务风电场包含350 台直驱风电机组。G1、G3、G4 和G5 的惯性时间常数和再热器时间常数分别为9.63 s 和10 s，G6、G9 和G10 的惯性时间常数和再热器时间常数分别为5.5 s 和15 s，其他参数见文献［28］。系统总负荷为2 850 MW，风电渗透率为25%。

设置节点23 的负荷为570 MW。t=60 s 时，模拟节点23 负荷馈线发生三相短路故障，故障0.2 s 后清除。直驱风电场母线电压、系统频率变化率/偏差、直驱风电场补偿功率和无功功率如附录E 图E1所示。由图E1（a）可知，电网故障期间的直驱风电场母线电压跌落至0.74 p.u.，并网点电压相角突变量为30°。由图E1（b）和（c）可知，本文所提方法计算的频率变化率和系统实际频率变化率基本一致，而忽略锁相暂态响应计算的频率变化率误差较大。t=63 s 时，系统实际频率偏差为0.34 Hz，本文所提方法计算的系统频率偏差为0.26 Hz，而忽略锁相暂态响应计算的系统频率偏差为0.48 Hz，误差较大。本文所提方法求解的系统最大频率偏差为0.52 Hz，忽略锁相暂态响应计算的系统最大频率偏差为0.54 Hz，2 种方法的计算结果差别较小。如图E1（d）所示，直驱风电场实际有功出力降低0.40 p.u.，本文所提方法下直驱风电场有功出力降低0.42 p.u.；忽略锁相暂态响应时的直驱风电场补偿功率为-0.27 p.u.，本文所提方法下补偿功率计算误差不超过5%。故障期间，直驱风电场提供0.26 p.u.的无功功率支撑，如图E1（e）所示。锁相暂态响应引起的功率控制误差计算结果如附录E图E2 所示，其中，第1 次功率控制误差最大为0.23 p.u.，第2 次功率控制误差最大为0.19 p.u.。

改变节点23 的负荷为1 425 MW。t=60 s 时，模拟节点23 负荷馈线发生三相短路故障，故障0.2 s后清除。电网故障期间的直驱风电场母线电压跌落至0.73 p.u.，并网点电压相角突变量为25°。故障期间，直驱风电场发出0.31 p.u.的无功功率支撑并网点电压，故障切除后，直驱风电场吸收部分无功功率防止过电压，如附录F 图F1 所示。本文所提方法计算的频率变化率与系统实际频率变化率基本一致。本文所提方法计算的系统最大频率偏差误差更小。由图F1 可知，直驱风电场实际有功出力降低0.73 p.u.，本文所提方法下直驱风电场有功出力降低0.72 p.u.，忽略锁相暂态响应时，直驱风电场补偿功率为-0.63 p.u.，误差较大。锁相暂态响应引起的2 次功率控制误差最大值均为0.20 p.u.，如附录F图F2 所示。上述算例结果表明，本文所提方法能够准确解析不同负荷切除率下的系统暂态频率特性。

5 结语

随着新能源渗透率的增加，电网故障下DDWT的综合惯量控制使电力系统的频率响应特性更加复杂。电网发生故障时，DDWT 并网点电压相角突变引发锁相暂态响应，导致DDWT 输出功率出现控制误差，从而改变电力系统的暂态频率特性。为此，通过量化锁相暂态响应引起的功率控制误差，建立了改进的SFRM，解析了电网故障下系统频率变化率和最大频率偏差等响应特性。

所提方法刻画了锁相暂态响应引起的功率控制误差对系统暂态频率的影响，分析了电网故障下的暂态频率响应特性，可为电网故障下风电系统的频率安全评估和紧急控制提供参考。电网拓扑变化、电源或负荷投切等扰动下，DDWT 并网点电压相角发生变化，同样可能产生锁相偏差，进而导致功率控制误差。因此，所建立的SFRM 以及解析的暂态频率响应特性可扩展应用于更多的电网扰动情况。

本文考虑了电网电压变化对系统频率特性的影响，但电网故障下风电场内的电压差异性有待进一步考虑，特别是尾流效应导致风电场内务机组调频能力不同对系统频率特性的影响仍有待深入研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。