基于代价参考粒子滤波器组的多目标检测前跟踪算法

卢 锦 马令坤 吕春玲 章为川 Sun Chang-Ming

低信噪比情况下的多目标跟踪是雷达、声呐、红外探测、图像处理等领域面临的难题之一,其目的是从观测数据中估计时变的多目标状态,包括目标数量、位置等信息.传统先检测后跟踪方法难以有效处理低信噪比目标[1-2].为提高低信噪比目标的检测和跟踪性能,学者们提出检测前跟踪(Trackbefore-detect,TBD)方法.TBD 方法从未经门限检测的原始观测数据中同时检测和跟踪低信噪比目标[3-8].实现多目标TBD 的算法主要包括粒子滤波[9-11]、概率假设密度(Probability hypothesis density,PHD)[12-13]、多目标伯努利滤波器[14]等.

文献[9]针对第2 个目标自第1 个目标产生的双目标跟踪与检测问题,提出基于粒子滤波的多目标TBD 方法,该方法是文献[6]中单目标粒子滤波的多目标检测前跟踪算法(Particle filter based track-before-detect,PF-TBD)方法的拓展.但随着目标数量的增加,该计算计算量急剧增加,效率较低.文献[10]提出一种多模型多目标TBD 方法.该方法需假设最大目标数量,首先,估计所有可能的目标存在组合或模式及其对应的联合后验概率密度和目标模型的概率;然后,整合不同模式下目标对应的状态向量,获得所有目标的状态估计.但随着目标数量的增加,该方法会出现算法结构复杂、计算量大问题.文献[11]提出一种基于粒子滤波的多目标TBD 算法,该方法假设最大的目标数量,用同样数量的样本表示每个目标的状态和存在情况,再联合估计所有目标的联合后验概率密度,据此估计各个时刻的目标状态和数量.随着目标数量的增加,该方法中的粒子数将成倍增加,因此也存在计算量大的问题.

PHD 和多目标伯努利滤波器是基于随机有限集(Random finite set,RFS)的多目标贝叶斯滤波器[12-14]的近似.基于RFS 的多目标贝叶斯滤波器将多目标状态和观测视为RFS,估计此RFS 的后验概率密度函数.文献[12]提出基于PHD 的单传感器TBD 方法(Probability hypothesis density based track-before-detect,PHD-TBD),实现红外图像多目标跟踪.文献[14]针对图像观测,提出基于多伯努利滤波的TBD 算法.

然而,无论是基于粒子滤波的TBD 方法,还是基于RFS 的TBD 方法,都将多目标视为整体,估计多个目标的联合状态的后验概率密度函数.随着目标数量的增加,必然会出现算法结构复杂、计算量大问题.针对上述问题,在单传感器条件下,本文提出一种基于代价参考粒子滤波器组的多目标TBD方法(Cost-reference particle filter bank bas-ed multi-target track-before-detect,CRPFB-MTBD).该方法是文献[15]基于代价参考粒子滤波器组的单目标TBD 方法的拓展.CRPFB-MTBD 首先将多目标检测与跟踪问题转化为多个单目标检测与跟踪问题,序贯地估计各个目标的状态序列;然后,通过比较各个目标航迹之间的距离来删减多余目标,从而最终确定目标数量和航迹.该方法无需假设目标数量,算法结构与目标数量无关,可并行执行,运行时间极短.仿真结果表明,与基于粒子滤波和RFS 的TBD 算法相比,本文方法可有效估计时变的多目标数量和状态,且运行时间极短.

1 状态空间模型

1.1 目标模型

假设k时刻有Nk个目标以特定的强度水平在x-y平面运动,离散运动模型为:

式中,vl,k表示k时刻第l个目标的过程噪声服从零均值协方差为Q的高斯分布,且在帧间、分辨单元间,各个目标间相互独立;k表示观测时刻,k=1,···,K;xl,k表示k时刻第l个目标的状态向量:

式中,[·]T表示向量的转置.(xl,k,yl,k) 和分别表示k时刻第l个目标的位置和速度,l=1,···,Nk,k时刻可能同时存在Nk个目标.F表示转移矩阵,定义如下:

式中,△T表示采样时间,⊗表示克罗内克积.Q定义如下:

式中,q1表示目标运动的噪声水平.由于本文方法无需目标强度信息,故在目标模型中并未包含对目标强度信息的估计,但传感器模型中包含目标强度.为方便起见,定义第l个目标在k时刻的强度为Il,k.

1.2 传感器模型

红外传感器提供某一监测区域的二维图像序列,每幅图像包含N×M个分辨单元(像素).一个分辨单元对应一个△x×△y的矩形观测区域,第 (i,j) 个分辨单元对应的观测区为(i△x×j△y),i=1,···,N,j=1,···,M.

以△T为间隔记录测量图像,k时刻,第(i,j)个分辨单元的测量强度为:

式中,Sk(l)∈{0, 1} 表示k时刻第l个目标出现或消失状态;表示k时刻第l个目标对于第 (i,j) 个分辨单元的强度水平的贡献,k时刻第(i,j)个分辨单元的强度水平是所有目标的强度水平之和;是第 (i,j) 个分辨单元的背景噪声,假设其在帧间、像素间相互独立且服从零均值、方差为σ2的高斯分布.本文采用传感器扩散模型,近似为式(6),表示强度为Il,k、位置为(xl,k,yl,k) 的点目标对于第 (i,j) 个分辨单元的强度贡献:

式中,Σ 是已知参数,表示传感器的模糊系数.

信噪比(Signal-to-noise ratio,SNR)定义为:

综上,从1 到K时刻的观测序列为: 1≤i ≤N,1≤j ≤M,1≤k ≤K},多目标跟踪的目标是从观测序列ZK中估计目标的数量,并估计每个目标的状态序列,先验信息为 0≤xl,k ≤N△x,0≤yl,k ≤M△y.

2 基于代价参考粒子滤波器组的多目标检测前跟踪算法

针对线性或分段线性运动模型,文献[15]提出CRPFB,实现了单目标的快速检测和跟踪.本节基于CRPFB,提出未知数量的多目标TBD 方法.

2.1 代价参考粒子滤波器组

基于式(1)和式(5)的状态空间模型,CRPFB基本结构如图1 所示.CRPFB 包含Ms个并行的代价参考粒子滤波器(Cost-reference particle filter,CRPF).每个CRPF 采用不同的先验信息,获得不同估计结果比较各个CRPF的累积代价将累积代价最大(或最小,与累积代价的定义有关)的CRPF 的估计结果作为CRPFB 的估计结果.CRPFB 中并行CRPF 数量Ms是一个较难确定的参数,类似于粒子滤波中的样本数量(粒子数).因此,CRPFB 性能会随Ms的增加而增加,但不会一直增加.本文通过对比不同Ms对算法性能的影响,来选择合适的Ms数量.

图1 CRPFB 的基本结构Fig.1 Basic structure of CRPFB

步骤1.先验信息计算.图1 中蓝色背景框部分表示第ms个CRPF 的先验信息,其计算原理及过程如下.

基于式(1)中的线性运动模型(系统噪声为零均值),第l个目标在k时刻的状态为其在x方向的运动速度的期望为常数:

进一步地,可从各个时刻第l个目标在x方向的位置来估计:

由式(9)可得,当xl,1=xms,xms ∼U(0,N△x),U(·,·) 表示均匀分布,考虑到 0≤xl,K ≤N△x,可得:

同理,当yl,1=yms,yms ∼U(0,M△y),考虑到0≤yl,K ≤M△y,第l个目标在y方向的速度均值的范围为:

基于式(10)和式(11)的假设和结论,将速度的均值近似为速度,则第l个目标的先验信息如表1所示.

表1 第 l 个目标的先验信息Table 1 Apriori information for the l -th target

图2 对比了原始先验信息(0≤xl,k ≤N△x,0≤yl,k ≤M△y)与表1 先验信息.在图2 中,矩形框为观测区域,对应第l个目标(包括每个目标)原始先验信息,阴影部分面积为表1 先验信息.由图2 可以看出,基于上述结论,当初始时刻目标位置确定时,目标的先验信息精度可大幅提高.

图2 原始先验信息与表1 先验信息的对比Fig.2 Comparison of original prior information and the prior information in table 1

步骤2.代价参考粒子滤波器.假设Ms个不同的目标初始位置,根据表1 可获得Ms种精确的先验信息.文献[15]指出,当Ms足够大时,CRPF 的样本数可取1.将观测序列ZK和Ms种先验信息输入Ms个 CRPF 中,可获得Ms种估计结果.各个CRPF在运行中相互独立,只在滤波结束后比较累积代价,因此CRPFB 具有完全的并行结构,其运行时间仅由单个CRPF 运行时间和累积代价的比较过程决定.

图1 中橙色背景框部分为第ms个CRPF 的滤波过程,仅有1 个目标,样本数设置为1 时,CRPF的估计过程如下.

步骤3.CRPFB 的状态估计.图1 中的绿色背景框部分即为CRPFB 的状态估计过程,其具体过程如下.

Ms个CRPF 共获得Ms个估计结果{,···,}.比较Ms个估计结果的累积代价,将累积代价最大的CRPF 的状态序列作为CRPFB 的估计结果,对应的累积代价记为Ccum:

与一般粒子滤波算法相比,CRPFB 中的CRPF 仅有一个样本,故无需重采样过程,可并行运行大量具有不同初始状态的CRPF,实现对目标状态序列的估计.

2.2 基于CRPFB-MTBD 算法

基于上述的CRPFB,本文提出CRPFB-MTBD 算法.该算法包括3 个连续过程,如图3 所示.1)获得所有可能目标的状态序列.当全部观测数据输入后,序贯地应用CRPFB,获得所有可能目标的状态序列;2)关联过程(估计目标数量).比较所有可能目标航迹间的欧氏距离,删除距离相近航迹中累积代价较小者,从而确定观测时段内出现的总体目标数量;3)判断各个目标出现的具体时刻.根据各状态序列累积代价的幅度变化特点,确定目标出现的具体时刻.

图3 CRPFB-MTBD 算法基本框架Fig.3 Basic structure of CRPFB-MTBD

1)获得所有可能状态序列

图4 是基于CRPFB-MTBD 算法的步骤1,估计所有可能的目标航迹.在该过程中,首先输入观测数据ZK,执行第1 次CRPFB.若CRPFB 的累积代价大于门限V1,则从ZK中减去CRPFB 的估计观测,再次输入CRPFB.此过程可执行若干次,直到CRPFB 的累积代价小于等于V1.当虚警概率Pfa给定,V1可通过对大量无目标的观测累积代价排序获得.图4 中,表示第l次CRPFB 的估计结果,l个目标的估计观测之和,Cl,cum表示第l个CRPF的估计状态序列的累积代价.若上述过程共经过l次CRPFB 滤波,则该步骤输出l个估计结果{,},即为所有可能目标的状态序列.表示第1 到第

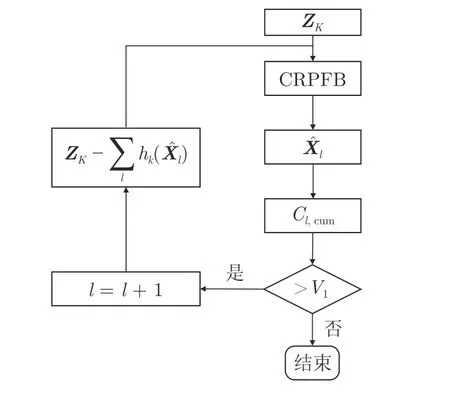
图4 估计可能的目标状态序列Fig.4 Estimation of all possible targets' state sequences

2)关联过程(估计目标数量和相应的状态序列)

图5 是基于CRPFB-MTBD 算法的第2 个步骤,估计观测时段内总的目标数量.将1)中获得的所有可能目标的状态序列 {,,···,} 排列组合,计算各估计结果之间的欧氏距离.d()即为第li个估计结果与第π(li)个估计结果的欧氏距离,如式(14)所示.当2 个的状态序列的欧氏距离小于等于给定门限V2时,删除累积代价较小的的状态序列.门限V2会随应用场景和分辨率等的不同而变化,因此难以确定.本文通过仿真实验,对比不同V2时算法的性能,来确定门限V2值.剩余航迹的个数即为观测时段内出现的目标数量.图5 中,即为lest个目标的可能的状态序列:

图5 估计目标数量Fig.5 Estimation of target number

3)判断各个目标出现的具体时刻

基于CRPFB-MTBD 算法假设各个目标在各个时刻都存在,而在实际中,各个目标出现的时刻可能不同.因此,本步骤判断各个目标存在的具体时刻,图6 是判断各个目标出现和消失的具体时刻.

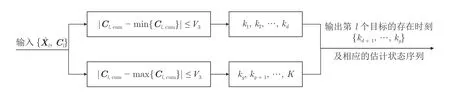
图6 判断各个目标存在的具体时刻Fig.6 Determination of the specific moments when each target existing

首先,输入2)估计到的第l个目标的估计状态和累积代价Cl,其中Cl={Cl,1,Cl,2,···,Cl,K},l=1, 2,···,lest,Cl,k为第l个目标在第k时刻的代价.

然后,比较Cl,cum与 min{Cl,cum}、Cl,cum与max{Cl,cum},以确定第l个目标出现和消失的时刻.其中表示第l个目标在第k时刻的累积代价.min{Cl,cum} 和 max{Cl,cum} 分别表示Cl,cum中的最小值和最大值.当 |Cl,cum-min{Cl,cum}|小于等于V3时,没有目标回波累积,即k1,k2,···,kd时刻目标不存在;当 |Cl,cum-max{Cl,cum}|小于等于V3时,目标回波也没有累积,即kg+1,···,K时刻目标未出现.

最后,输出第l个目标的存在时刻kd+1,···,kg和相应的状态序列.

经过上述3 个连续过程,即可基于CRPFB 估计未知数量的目标和状态序列.其中,过程1)和3)可并行执行,能够极大缩短计算时间.

3 仿真实验及分析

仿真实验包括2 个部分: 1)比较本文基于CRPFB-MTBD 算法与基于传统粒子滤波的多目标检测前跟踪算法(Particle filter based multi-target track-before-detect,PF-MTBD)[11]、PHD-TBD[12]和基于伯努利滤波的TBD 方法(Bernoulli based track-before-detect,Bernoulli-TBD)[14]的性能;2)对影响CRPFB-MTBD 性能的因素进行分析.

3.1 CRPFB-MTBD 与现有方法的性能对比

在仿真实验1)中,通过检测和跟踪变化数量的目标来比较CRPFB-MTBD、PF-MTBD、PHDTBD 和Bernoulli-TBD 在目标数量估计、目标状态序列估计、运行速度等方面性能.其中,目标数量估计和目标状态序列估计通过最优次模式分配准则(Optimal subpattern assignment metric,OSPA)[16-17]来评判.在多目标跟踪中,OSPA 评估观测时段内估计的目标状态序列集合与真实目标状态序列集合之间的差距,包括OSPA 位置误差、OSPA势误差和两者的组合OSPA 总体误差.具体计算公式和Matlab 代码可参见文献[16-17].此外,通过相同平台,对算法的运行速度与各算法的平均单次运行时间进行比较.

仿真环境设置如下: 假设观测区域内存在3 个目标,其初始状态分别为x1,1=[17, 0, 13,-0.13]T,x2,1=[4, 0.2, 4, 0.2]T,x3,1=[3, 0.2, 17, 0]T,q1=0.001.目标强度由式(7)的SNR 决定,q2=0.010.整个检测和跟踪过程持续时间为60 s,采样时间△T=1 s,像素分辨单元△x=△y=1 m,监测区域大小为 3 0 m×30 m 的序列图像,传感器模糊系数Σ=0.7.假设背景噪声为方差σ2=1 的高斯噪声,目标的运动方程如式(1)所示.目标1 在第5 帧进入监视区域,在第60 帧消失;目标2 在第15 帧进入监视区域,在第55 帧消失;目标3 在第10 帧进入监视区域,在第40 帧消失.图7 是当SNR=10 dB时,第2 帧(无目标)、第14 帧(1 个目标)、第35 帧(3 个目标)和第55 帧(2 个目标)的一次观测图.由图7 可以看出,当SNR=10 dB 时,很难直接从图像上判断目标的数量和位置.

各算法参数和条件设置如下: 1) PF-MTBD.设最大目标数量为5,每个目标的样本数为10 000;2) PHD-TBD.每帧中搜索新生目标的粒子数为2 500,每个期望目标对应的样本数为2 000,其他参数设置与文献[12]相同;3) Bernoulli-TBD.设最大目标数量为100,每个伯努利滤波器中生存样本数量为5 000,新生样本数量为2 000,存在概率门限为0.5;4) CRPFB-MTBD.CRPF 数量Ms=3 0 000,每个CRPF只采用1个粒子,当Pfa=10-3时,门限V1=101.097 9,V2=6.000 0,V3=8.884 0.在信噪比分别为8 dB、6 dB 时,分别进行100 次蒙特卡洛仿真,对比4 种方法的OSPA 结果.OSPA 参数为c=5,p=2.

图8、图9 分别表示当SNR 为6 dB、8 dB,3个目标时,4 种方法的OSPA.图8(a)和图9(a)表示OSPA 总体误差随时间变化情况,图8(b)和图9(b)为OSPA 位置误差随时间变化情况,图8(c)和图9(c)为OSPA 势误差随时间变化情况.由图8 和图9 可以看出,CRPFB-MTBD 的目标数量和目标状态估计性能均优于PF-MTBD、PHD-TBD 和Bernoulli-TBD.由图9 可以看出,CRPFB-MTBD 方法对于位置较近的目标有一定的区分能力.图10 和图11为当SNR=8 dB、3 个目标时,CRPFB-MTBD 方法的目标状态序列估计结果和目标数量估计结果.

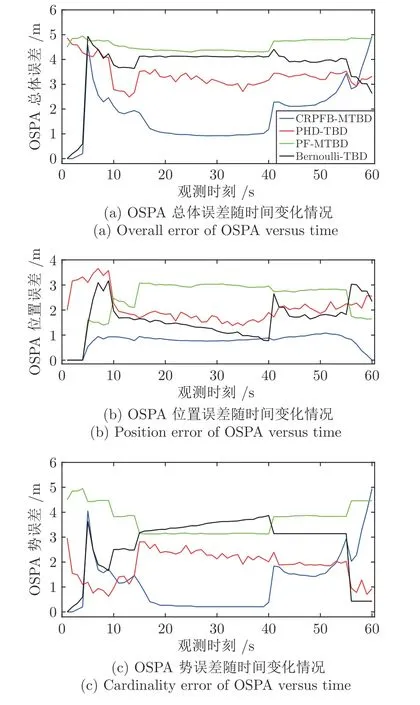
图8 当SNR=6 dB,3 个目标时,4 种方法的OSPAFig.8 Comparison of OSPAs resulted from 4 algorithms when SNR=6 dB and 3 targets

图9 当SNR=8 dB,3 个目标时,4 种方法的OSPAFig.9 Comparison of OSPAs resulted from 4 algorithms when SNR=8 dB and 3 targets

图10 当SNR=8 dB,3 个目标时,CRPFB-MTBD 的目标状态估计结果Fig.10 State estimation of CRPFB-MTBD when SNR=8 dB and 3 targets

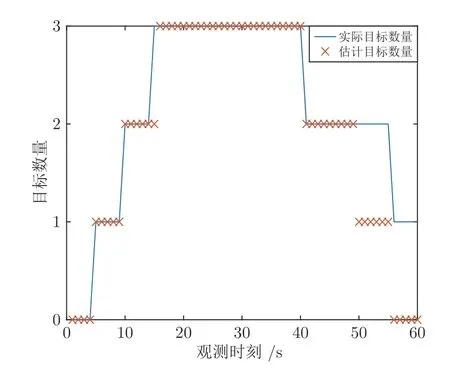
图11 当SNR=8 dB,3 个目标时,CRPFB-MTBD 的目标数量估计结果Fig.11 Estimation of target number provided by CRPFB-MTBD when SNR=8 dB and 3 targets

表2 为仿真实验1)的4 种算法平均单次运行时间比较.其中,CRPFB-MTBD 进行了10 次CRPFB 循环(在本次实验中,将CRPFB 的序贯运行次数设置为10 次;在实际运用中,CRPFB 的序贯运行次数不确定).由表2 可以看出,CRPFB-MTBD 的运行时间远小于其他3 种算法.原因是PFMTBD 和PHD-TBD 将所有目标视为整体,目标数量越多,所需样本数越大,运算量越大,且难以并行执行,故耗时长.虽然在Bernoulli-TBD 中,各个伯努利滤波器可并行执行,但每个滤波器中的样本数量较多,故Bernoulli-TBD 的运行时间也较长.CRPFB-MTBD 算法即使每次CRPFB 中包含的CRPF 数量达到30 000 个,但30 000 个CRPF 可并行执行,每个CRPF 只需要1 个样本,故耗时短.

表2 4 种算法的平均单次运行时间 (s)Table 2 Average single running time of 4 algorithms (s)

3.2 CRPFB-MTBD 性能影响因素分析

仿真实验2)分析目标的数量、并行CRPF 数量和门限对CRPFB-MTBD 算法性能的影响.

仿真环境和参数设置如下: 目标数量增加至5 个.5 个目标的初始状态分别为x1,1=[7, 0, 23, 0.1]T,x2,1=[30, 0.15, 4, 0.2]T,x3,1=[13, 0.2, 17, 0]T,x4,1=[40,-0.1, 40,-0.1]T,x5,1=[20, 0.1, 10, 0.2]T.CRPFB-MTBD 参数设置与仿真实验1)相同.

1)目标数量对CRPFB-MTBD 算法性能的影响.图12 为当SNR=6 dB,1、3、5 个目标时,100次CRPFB-MTBD 仿真的平均OSPA.由图12 可以看出,随着目标数量的增加,CRPFB-MTBD 的性能有所下降.

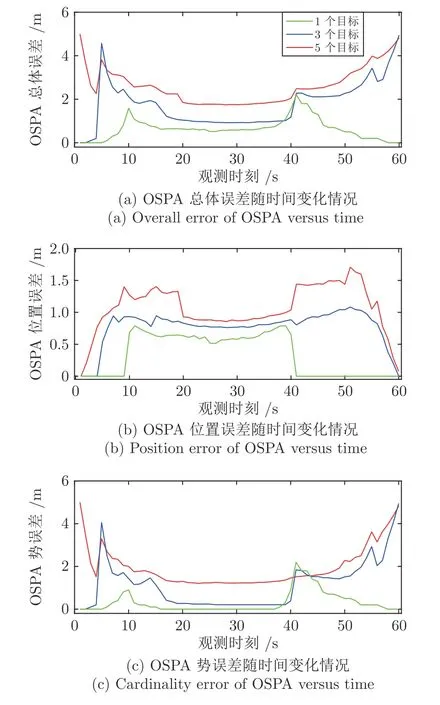
图12 当SNR=6 dB 时,目标数量对CRPFB-MTBD性能的影响Fig.12 Impact of target number on the performance of CRPFB-MTBD when SNR=6 dB

2)并行CRPF 数量对CRPFB-MTBD 算法性能的影响.图13 和图14 分别比较3 个和5 个目标情况下,当SNR=6 dB,CRPF 的数量分别为1 000、2 000、3 000、5 000、10 000、20 000、30 000 时,100次仿真实验的平均OSPA.由图13 和图14 可以看出,随着CRPF 的数量的增加,CRPFB-MTBD 性能逐步提升.当CRPF 的数量超过5 000 时,性能逐渐稳定;随CRPF 数量的增加,仍有小幅提高.但针对某个具体问题,CRPF 数量如何设置,仍有待进一步研究,此问题类似粒子滤波中粒子数量的设置.

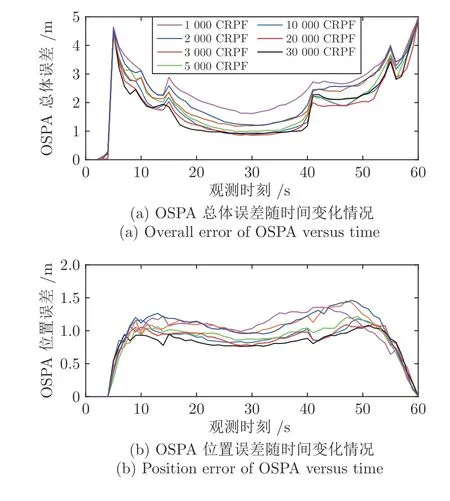
图13 当SNR=6 dB,3 个目标时,CRPF 数量对CRPFB-MTBD 性能的影响Fig.13 Impact of the number of CRPFs on the performance of CRPFB-MTBD when SNR=6 dB and 3 targets

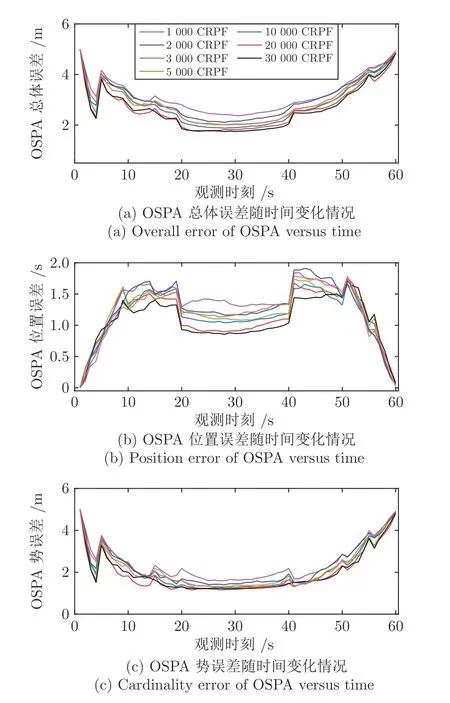
图14 当SNR=6 dB,5 个目标时,CRPF 数量对CRPFB-MTBD 性能的影响Fig.14 Impact of the number of CRPFs on the performance of CRPFB-MTBD when SNR=6 dB and 5 targets

3) 门限对CRPFB-MTBD 算法性能的影响.在本次仿真实验中,CRPFB-MTBD 算法的参数设置与仿真实验1)相同.如第2.2 节所述,CRPFBMTBD 包含V1、V2、V3三个检测门限.其中V1和V3可根据观测给定虚警估计,V2是经验值.门限V2至关重要,一方面用于确定观测时段内出现的目标数量,另一方面用于确定目标的可能状态序列.在仿真实验1)中,V2设置为6.图15、图16 比较了当3 个和5 个目标情况下,V2为4, 6, 8, 10 时,100 次仿真的平均OSPA.由图15 和图16 可以看出,针对本文设置的仿真情况,当V2=6 时,算法的势估计性能(即目标数量估计性能) 最好;当V2=10时,算法的位置估计误差(即目标状态序列估计性能)最好.综合考虑势误差和位置误差,故设置V2=6.

图15 当SNR=6 dB,3 个目标时,门限 V2 对CRPFB-MTBD 性能的影响Fig.15 Impact of threshold V2 on the performance of CRPFB-MTBD when SNR=6 dB and 3 targets

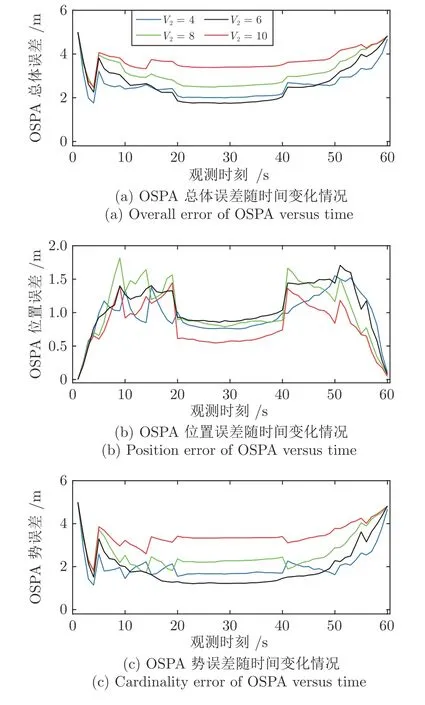
图16 当SNR=6 dB,5 个目标时,门限 V2 对CRPFB-MTBD 性能的影响Fig.16 Impact of threshold V2 on the performance of CRPFB-MTBD when SNR=6 dB and 5 targets

仿真实验结果表明,与现有经典方法相比较,本文提出的CRPFB-MTBD 算法的估计性能、运算速度均有明显提高.实验结果表明,随着目标数量的增加和信噪比的下降,CRPFB-MTBD 算法性能会有所下降.此外,并行CRPF 的数量和门限V2的选择,也会对CRPFB-MTBD 的性能有所影响.

4 结束语

针对图像序列中多目标检测问题,基于CRPFB提出一种新颖的低信噪比多目标估计方法.与现有方法相比较,该方法将多目标估计问题转化为多个单目标检测和估计问题,打破了现有的将多目标视为整体的思路.与现有几种经典算法进行对比实验,结果表明: 与性能最佳的PHD-TBD 相比,CRPFBMTBD 的目标数量估计和位置估计精度提高了约50%,如图8 和图9 所示;与运行速度最快的Bernoulli-TBD 相比,CR-PFB-MTBD 运行速度提高了约600 倍,如图2 所示.由不同影响因素的仿真实验结果可以看出: 1)随着目标数量的增加,CRPFBMTBD 的估计性能会下降;2)并行CRPF 数量对CRPFB-MTBD 性能影响很大,只有在CRPF 的数量足够大时,CRPFB-MTBD性能才会趋于稳定;3)门限V2的选择直接影响CR-PFB-MTBD 性能.上述图8～ 图16 和表2 仿真实验结果表明,针对在图像序列中检测和跟踪较低信噪比的多目标问题,本文提出的CRPFB-MTBD 算法以极短的运行时间获得了检测性能、估计性能的可观改善.但CRPFB-MTBD 算法采用仿真分析方法确定并行CRPF 数量和门限V2等参数,这不利于该算法的广泛应用.在后续研究中,将进一步研究这些参数与应用场景的关系,进而确定参数的选取原则.