基于波束优化赋形方法的斜视星载SAR模糊抑制研究

王长城,张 毅,张永伟,王 伟

(1.中国科学院空天信息研究院,北京 100190;2.中国科学院大学 电子电气与通信工程学院,北京 100049)

0 引 言

距离模糊与方位模糊会对星载合成孔径雷达(Synthetic Aperture Radar,SAR)的成像质量带来不利影响。对传统的单通道SAR而言,提高脉冲重复频率(Pulse Repetition Frequency,PRF)有助于改善方位模糊,但PRF的升高会增加距离模糊区的数目,增多并缩短其与测绘区的距离,从而降低系统距离模糊抑制的性能。这意味着SAR的模糊性对系统参数设计带来了限制。为了抑制距离模糊和方位模糊,学者们提出了许多方法[1-5],这些方法会提高系统复杂度或只能应用于某些特定情况,而波束赋形算法则没有上述限制。现阶段,通过天线波束赋形来抑制星载SAR的模糊性的方法[6-14],大多是在一定的PRF下,假定接收天线的权重为可分离型分布,仅对俯仰向波束进行优化,在保持方位模糊的同时降低距离模糊。但这类方法都是建立在雷达正侧视的情况下。在通过改变卫星姿态等方式实现SAR斜视时,天线旁瓣对应的模糊区可能与测绘区不在同一多普勒频段内,这时传统的距离模糊比指标不能准确地衡量距离模糊的实际大小;同时,在雷达斜视情况下,权重为可分离型分布的天线阵列在调整俯仰向阵元幅值相位分布时,也会对波束在雷达方位向上的旁瓣幅值产生较大的影响,此时继续忽略雷达方位向波束会造成较大的误差。因此,文献[6-14]的方法不再适用。文献[15]初步考虑了斜视的情况,给出了模糊比关于天线权重的数学模型,但并未考虑到与成像区关于星下点-雷达速度平面所对称的镜像模糊区,以及由调整卫星姿态实现SAR斜视时天线波束的变化;同时,其采用了与文献[10]中类似的优化方法。该方法在纳入计算的模糊区过多时,比起抑制模糊区对应的旁瓣幅值以降低模糊能量的进入,更倾向于扩展主瓣使天线波束在测绘区的指向上形成最大增益,一方面,天线的旁瓣水平会有所增加;另一方面,波束主瓣在方位向的展宽,会直接改变方位模糊区的大小,进而改变原本的优化目标。

针对上述问题,本文从星载SAR模糊成因出发,给出了建立模糊比-天线权重优化模型的一般思路,并充分考虑了包含星下点对侧镜像区在内的模糊区及不同的斜视模式,丰富了模糊比模型的内涵;之后用二次锥方法,以模糊能量作为优化目标,约束波束主瓣宽度及旁瓣幅值,求解得到阵列单元幅度相位分布。该方法在保证方位向带宽不变、尽可能维持旁瓣水平的同时,降低了模糊比的大小。仿真实验验证了本文方法的有效性。

1 理论基础

1.1 距离-方位模糊分析

星载SAR的模糊[16],可以划分为距离模糊和方位模糊。距离模糊是指当旁瓣照射区回波的双程时延与测绘区期望回波的双程时延相差脉冲重复周期的整数倍时,旁瓣回波与期望回波叠加所产生的模糊;方位模糊指多普勒频率高于脉冲重复频率的回波信号折叠到期望信号多普勒频带内,造成的信号在频谱混叠。两者在天线阵元权重为可分离型分布时,可以分别由距离模糊比和方位模糊比来衡量。在雷达处于正侧视时,雷达方位向、距离向与天线方位向、俯仰向一一对应,此时,即便天线安装角会使得雷达天线有初始仰角,也不会改变天线方位向与雷达距离向、天线俯仰向与雷达方位向之间的正交关系,因而采用波束赋形方法抑制模糊能量时,可以将距离模糊比、方位模糊比作分开考虑。而在斜视时,无论以何种方式,都会直接或间接破坏这两对正交关系,因而在单独调节天线某一维度阵元权重时,会同时对雷达的距离向、方位向波束造成影响。因此,天线权重不应再作为可分离型分布考虑,那么也无法再将距离模糊、方位模糊分别用距离模糊比、方位模糊比来衡量,必须将之综合考虑。为此,引入模糊比的概念。

星载SAR的模糊比[16](Ambiguity to Signal Ratio,ASR)定义为回波时延或多普勒频移造成的同目标混叠的模糊能量与期望目标能量强度之比。下面将给出ASR的准确表达式。

星载SAR的回波功率[15,17]可以表示为回波时延td与多普勒频率fd的函数：

(1)

式中：K由雷达系统参数确定;σ0为后向散射系数;η(·)为入射角;∘为复合函数标识;Gt(·)为发射天线功率方向图;Gr(·)为接收天线功率方向图;R(·)为斜距。后向散射系数可由文献[18]给出的经验公式来代替,如下所示：

σ0=p1+p2exp(-p3η)+p4cos(p5η+p6)

(2)

式中：参数p1～p6的选取与雷达天线的极化类型及照射地物的种类有关。

为了计算式(1),需建立(td,fd)与下视角α、斜视角θsq间的联系。时延td关于斜距R、多普勒频率fd关于斜视角θsq的关系为

(3)

(4)

式中：c为光速;v为轨道速度;λ为波长。进一步根据文献[19],将地球近似为半径为Re的正球体,假定卫星轨道高度为H,结合图1所示的SAR几何关系,有

(5)

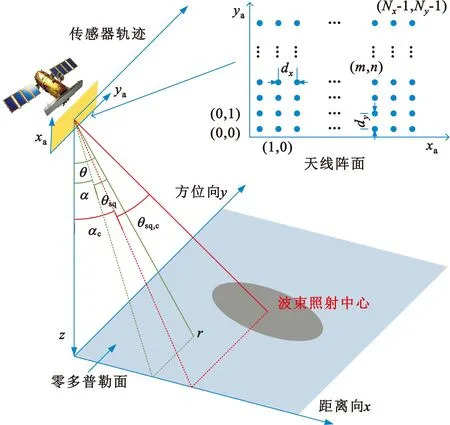
图1 SAR几何关系与相控阵天线阵面Fig.1 The geometry of SAR and phased array antenna

(6)

(7)

式中：θ为星下点离线角;β为地心角。由式(3)～(7)可知,对于(td,fd)所确定的雷达波束照射的一点,可以由相应的(α,θsq)确定,同时还存在着其关于星下点与雷达速度矢量确定的平面对称的镜像区内一点(-α,θsq)与之有相同的时延和多普勒频率。

为了将镜像模糊区纳入考量,将式(1)改写为

(8)

由式(1)和式(8),测绘区回波的总能量可以表示为

(9)

I是在已知PRF情况下由时延和多普勒频率(td,fd)确定的测绘区内一点,其模糊能量可以表示为

(10)

式中：Nr1为从星下点到测绘区近端范围内的距离模糊区数;Nr2为从测绘区远端到地球边界范围内的距离模糊区数;Na1为测绘区多普勒频带至最小多普勒频率-2v/λ之间以PRF划分的方位模糊区数;Na2为测绘区多普勒频带至最大多普勒频率2v/λ之间以PRF划分的方位模糊区数;tir=td+ir/PRF,fia=fd+ia·PRF。由式(9)～(10)可知,测绘区对应的包含镜像区在内的所有模糊区能量之和为

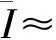
(11)

式中：(αir,it,θsq,ia,if)为(tir,it,fia,if)的映射,tir,it=tit+ir/PRF;fia,if=fd+if·PRF;(-αir,it,θsq,ia,if)为其在镜像区的对应点。

根据星载SAR的模糊比的定义,有

(12)

由式(1)和式(10)可知,ASR的大小主要取决于PRF以及雷达天线的辐射方向图,其中PRF的确定受到星下点回波、接收回波窗、多普勒带宽等多种因素的影响[19],不能随意取值。因此,在固定PRF的情况下,使用天线波束赋形方法来降低ASR。同时,注意到ASR的计算精度受到SAR回波功率方程及SAR成像几何模型等因素的影响,本文在计算模糊区回波方位时,将地球近似为球体,因而存在一定的误差,这可以随着SAR成像几何模型不断完善而逐步降低。

1.2 斜视模式对波束影响

星载SAR的斜视可以由调整卫星姿态或是相控阵天线波控码等方式来实现,可以明确地感受到,不同的方式对在1.1节中提到的两对正交关系会造成不同的影响,因此对天线波束也会造成不同的影响,不能一概而论。在这里,考虑3种相对比较理想的情况。

为获取天线方向图的准确表达,首先进一步明确雷达与天线间的几何关系。如图1所示,在雷达位置和波束在地面覆盖区的简单几何模型中,以SAR距离向为x轴,方位向为y轴,雷达指向星下点的矢量为z轴建立坐标系;同时,将天线阵面的俯仰向设为xa轴,方位向设为ya轴,则天线阵面到远区某点r的方向矢量r由该点对应的下视角α与斜视角θsq表示：

r=xsinαcosθsq+ysinθsq+zcosαcosθsq

(13)

因此若以电扫描的方式,将天线波束中心移动到下视角中心αc、斜视角中心θsq,c的位置,那么具有初始仰角θel的矩形栅格排布的平面相控阵天线,其阵因子方向图可以很容易表示为(α,θsq)的函数：

(14)

φ=mkuxdx+nkuydy

式中：(m,n)为天线阵元的俯仰向和方位向编号;wmn为编号(m,n)的阵元的复加权权重;Emn(α,θsq)为其辐射方向图;k为波速;dx为俯仰向阵元间距;dy为方位向阵元间距;Nx为俯仰向天线阵元数;Ny为方位向天线阵元数;(mkuxdx,nkuydy)为编号(m,n)的阵元与编号为(0,0)的参考阵元的波程差沿xa轴和ya轴的分量,其中包括了由天线初始仰角及波控码调节带来的波程差;uz为天线阵面法向量与方向矢量r的内积,uz>0表示其对应的(α,θsq)点在波束照射范围内。(ux,uy,uz)可以由(α,θsq)唯一确定,有

ux=sin(α-θel)cosθsq-sin(αc-θel)cosθsq,c

(15)

uy=sinθsq-sinθsq,c

(16)

uz=cos(α-θel)cosθsq

(17)

若以调节卫星姿态的方式,将波束中心置于斜视角中心θsq,c、下视角中心αc处,为尽量降低波束中心线上多普勒频率的变化[20],SAR平台的偏航角θyaw,俯仰角θpit,以及天线初始的仰角θel可以由式(18)～(20)得到：

tanθyaw=sinαctanθsq,c

(18)

sinθpit=cosαcsinθsq,c

(19)

(20)

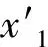
设从x轴相反方向观察将天线平面逆时针旋转θpit的旋转矩阵为

(21)

沿y轴相同方向观察将天线平面逆时针旋转θa的旋转矩阵为

(22)

沿z轴相同方向观察将天线平面逆时针旋转θyaw的旋转矩阵为

(23)

那么此时有

(24)

同样,可以用两者结合的方式,将天线波束心移动到指定位置,即通过调整横滚角使初始的天线阵面的仰角θel对准下视角中心αc,再调节波控码使波束中心至于斜视角中心θsq,c处。此时,

ux=sin(α-θel)cosθsq

(25)

而uy和uz与式(16)和式(17)相同。

在上述3种情况下,多普勒带宽Bd可以视为

(26)

式中：v为雷达平台速度;La为方位向天线长度。

1.3 基于二次规划的模糊比优化模型

为了使用波束赋形的方法优化模糊比,在本节中,将模糊比与天线权重直接联系起来,并以此为根据确立天线波束的优化方案。

式(14)中的天线阵因子方向图可以表示为矢量内积的形式：

Fr(α,θsq)=U(uz)wTe

(27)

式中：U(·)为阶跃函数;w为按天线阵面方位向展开的阵元权重矢量;e为对应的导向矢量,有

w=[w00…w0Ny…wNxNy]T

由式(27),天线功率方向图可以写为

|Fr(α,θsq)|2=U(uz)(wTe)(wTe)H=wTCw*

(28)

式中：

C(α,θsq)=(U°uz)(α,θsq)eH(α,θsq)e(α,θsq)。

根据上述推导,模糊能量和测绘区信号能量都可以写成二次型的形式。假定发射天线已经确定,那么双程天线功率方向图可以表示为

Gt(α,θsq)Gr(α,θsq)=wTC(α,θsq)w*

(29)

由此,式(8)可以改写为

S(α,θsq)=wTCs(α,θsq)w*

(30)

式中：

由式(9)、(11)、(30),有

(31)

(32)

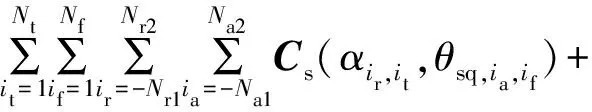
则模糊比可以表示为广义瑞利熵的形式：

(33)

尽管对于平面天线阵列,式(33)的形式可以直接求解得到最小值对应的阵元权重[15],但当天线阵元之间的波程差中包含的相位信息变得复杂或者模糊区数目庞大时,通过直接求解广义瑞利熵最小值得到的天线方向图,其旁瓣水平难以保证。受到文献[13-14]的启发,可以结合天线波束赋形的相关算法,增加约束条件或是适当调整目标函数,引入模糊能量相关的信息,在对波束进行赋形、保证天线主瓣宽度的同时,能够灵活地抑制模糊区对应的旁瓣幅值,从而降低模糊比的大小。然而,将文献[13-14]中所采用的优化方案应用于平面天线阵列时,其所需要的存储和计算成本会成几何倍增加,使用有限的资源无法完成优化运算;而智能优化算法,如遗传算法[21]等,虽然能够取得一定的效果,但无法维持天线的基本形状。为此,不得不考虑相对质朴的方案。

在文献[22]基础上改进的文献[23]中的天线波束赋形的方法如下：

(34)

s.t.wTe(αc,θsq,c)=1
|wTe(α,θsq)|≤Ls(α,θsq),(α,θsq)∈Θs

式中：w∈Nx·Ny为阵元复激励权重;e(α,θsq)∈Nx·Ny为(α,θsq)处的导向矢量;Ls(α,θsq)为(α,θsq)处设定的旁瓣幅值;Θs为旁瓣位置采样的集合。

在式(34)中加入模糊能量信息,可以得到目标函数为二次函数、约束为锥约束的二次锥规划问题(Quadratic Cone Problem,QCP),即

(35)

s.t.wTe(αc,θsq,c)=1
|wTe(α,θsq)|≤Ls(α,θsq),(α,θsq)∈Θs

式中：Ar∈Nx·Ny×Nx·Ny为模糊矩阵,注意到该矩阵正定;σ2为高斯白噪声的平均功率,其值可以由实际经验先验地决定,σ2I的引入有助于天线方向图旁瓣幅值的降低还有上述凸优化问题的收敛[10]。

为了求解式(35),需将式(35)中的目标函数实数化为

(36)

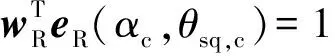
式中：Re(·)表示取向量或矩阵的实数部分;Im(·)表示取向量或矩阵的虚数部分。

由上述推导可知,D∈2Nx·Ny×2Nx·Ny为正定的实对称矩阵,根据文献[24],该形式的凸优化问题可以转化成标准的二阶锥问题,进而可以在CVXPY[25]及SCS求解器(Splitting Cone Solver)[26-27]的帮助下求解式(36)得到wR,从而完成对天线方向图的优化设计。

2 仿真实验

本节将对提出的模糊抑制方法进行仿真,并通过模糊比、峰值旁瓣比(Peak Side Lobe Ratio,PSLR)[19]、积分旁瓣比(Integrated Side Lobe Ratio,ISLR)[19]等指标来评价仿真结果。同时作为对比,给出了以文献[24]中基于二阶锥规划(Second-order Cone Programming,SOCP)的方向图综合方法对模糊区方向旁瓣进行抑制的结果。最后,使用优化前后的接收天线对点目标进行成像仿真,以进一步展示优化效果。

2.1 仿真参数

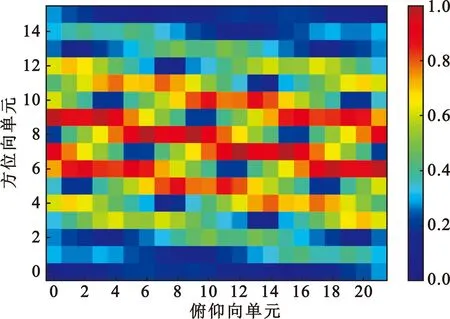
仿真使用L频段的雷达天线参数,对其接收天线——具有22×16的矩形栅格排布的平面阵列天线阵列进行了优化。天线结构如图3所示,由4个面板组成,每个面板包含4个模块,每个模块由22个子阵列构成,每个子阵列又有4个贴片单元,由同一个T/R组件控制,因此视每个子阵列为独立的辐射阵元。详细的仿真参数如表1所示。在该组参数下,模糊区的分布如图4所示,其中,黄色区域为模糊区,包含镜像区在内共有40(方位向)×49(距离向)×2-1个;红色区域为测绘区。仿真采用的发射天线及优化前的接收天线为均匀平面阵,斜视角由调整卫星姿态的方式取得,此方式可以缓解斜视带来的天线阵元之间在方位向和俯仰向上的耦合,其辐射方向图如图5(a)和(b)所示。

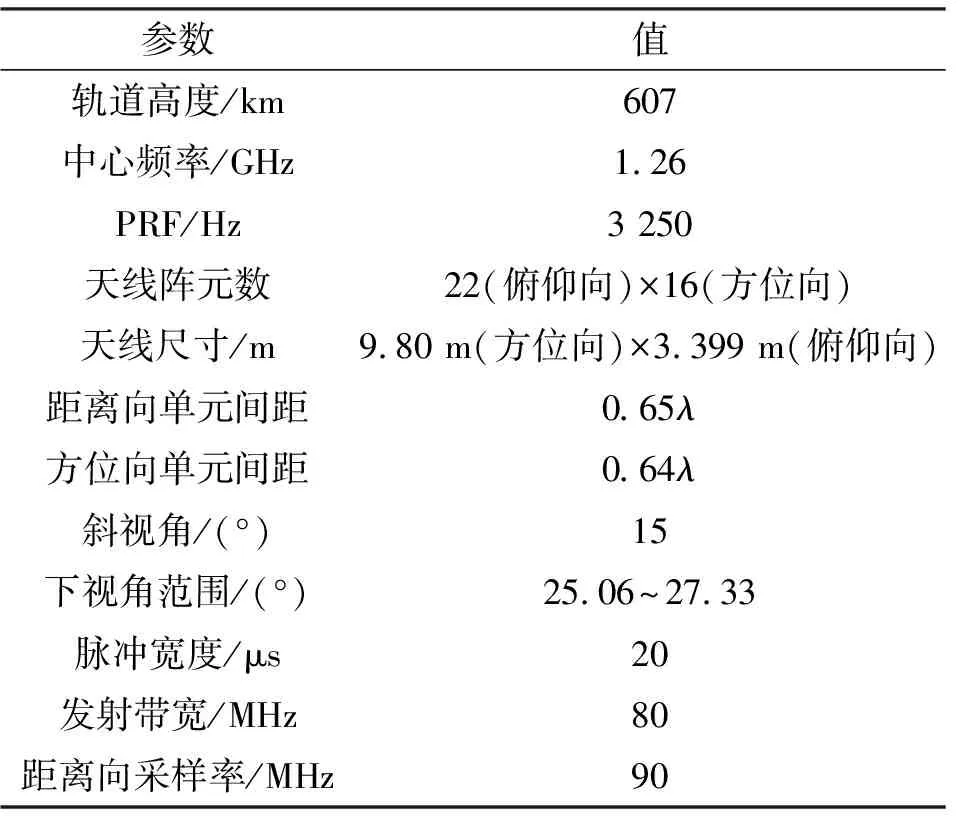
表1 仿真参数Tab.1 Simulation parameters

图3 天线结构Fig.3 Structure of antenna

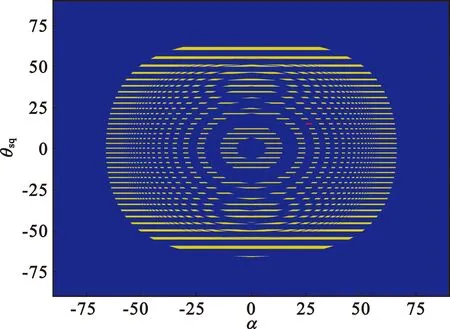
图4 模糊区分布Fig.4 Distribution of ambiguity region

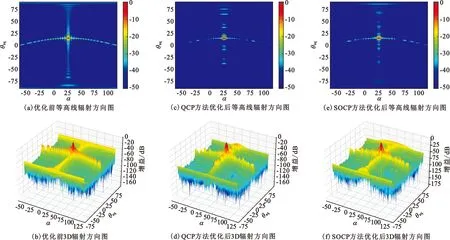
图5 接收天线辐射方向图Fig.5 Radiation pattern of receiving antenna

2.2 评价指标

模糊比外的评价指标定义如下：

PSLR指的是最大旁瓣同主瓣在高度上的比值,公式为

(37)

式中：Pmain,max为主瓣峰值;PSLL,max为最大旁瓣峰值。

ISLR为天线旁瓣功率与主瓣功率的比值,公式为

(38)

式中：Ptotal为总功率;Pmain是主瓣功率。

2.3 仿真结果

经QCP方法及SOCP方法优化后的接收天线辐射方向图分别由图5(c)、(d)及图5(e)、(f)给出,可以直观看出,优化后的接收天线主要是旁瓣幅值发生了变化。

优化前均匀加权的接收天线,PSLR为-13.25 dB,ISLR为-5.61 dB,ASR为-25.75 dB。经SOCP方法优化后的接收天线,PSLR为-15.10 dB,ISLR为-10.43 dB,分别下降了1.85 dB和4.83 dB;而优化后的ASR为-31.19 dB,降低了5.44 dB。经QCP方法优化后的接收天线,PSLR为-17.35 dB,ISLR为-13.45 dB,分别下降了4.1 dB和7.84 dB,而优化后的ASR为-36.54 dB,降低了10.79 dB,其各项指标降幅明显高于SOCP方法。

优化前及分别采用QCP方法及SOCP方法优化后的模糊比沿斜距分布的曲线如图6所示。在斜距方向上,优化前模糊比最小值ASRmin为-27.92 dB,SOCP方法优化后,模糊比最小值ASRmin为-36.99 dB,QCP方法优化模糊比最小值ASRmin为-42.16 dB。尽管在某些斜距上,SOCP方法优化后的模糊比要略优于QCP方法优化后的模糊比,但总体上,QCP方法优化后的模糊比要明显低于SOCP优化后的模糊比。表2是对上述定量指标的总结。

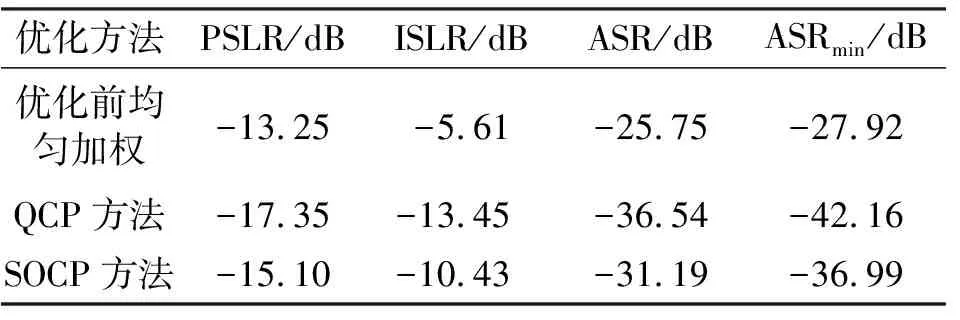
表2 优化前后PSLR、ISLR、ASR变化情况Tab.2 Changes in PSLR,ISLR,ASR before and after optimization

图6 优化前后模糊比-斜距曲线Fig.6 ASR-slant range curve before and after optimization

图7给出了经QCP方法及SOCP优化后的接收天线阵元权重的归一化幅值分布情况,优化后接收天线的权重幅值关于天线阵面中心对称。

(a)QCP方法

综上所述,QCP方法与SOCP方法都能够有效抑制星载SAR模糊比的大小,但对比各项指标,QCP方法要明显优于SOCP方法。

为了进一步阐释QCP方法有效性,将测绘区中心即(α,θsq)设置为目标点,同时在所有的模糊区对应位置放置了会与其叠加产生模糊的模糊点,各点的归一化后向散射系数由式(2)计算得到。为了凸显模糊抑制的效果,适当提高了模糊点回波能量。生成回波后,采用后向投影(Back Projection,BP)成像算法进行成像,成像的像素点数为256×256,成像结果如图8所示。图8(a)为在不考虑模糊点的情况下对目标点的成像仿真;图8(b)是在接收天线为均匀加权的矩形栅格分布的平面阵列天线时,引入模糊点之后对目标点进行成像的仿真结果,模糊点的能量在BP成像算法处理后,分散到了整个成像图片中;图8(c)是在接收天线经QCP方法优化后,在同样的模糊点干扰下,对目标点成像的仿真结果,可以看出优化后的接收天线抑制了模糊点的能量,提高了成像质量。

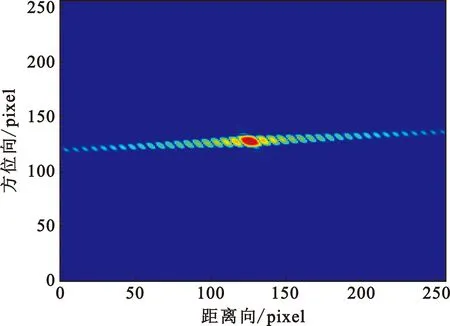
(a)无模糊

3 结 论

本文从星载合成孔径雷达模糊成因出发,结合星载SAR回波方程、星载SAR简单几何以及对均匀分布的平面天线阵列在星载SAR斜视情况下的辐射方向图分析,给出了计算模糊比的一般性思路,以此建立了模糊能量、测绘带回波能量、模糊比关于天线各阵元权重的模型。结合天线波束赋形的凸优化方法,提出了一种模糊比的优化方案,可以利用有限的资源完成对星载SAR接收天线方向图的综合。在L频段雷达天线上的仿真结果表明,该方案可以在保持方位向带宽及天线方向图基本形状的前提下,调节模糊区旁瓣幅值,实现对模糊能量的抑制,成功降低了模糊比。对点目标的成像仿真进一步展示了方法的有效性。