一种共址平台装备的射频干扰抑制系统设计方法

唐 聪,高 昕,朱宏权,张金荣,张中山,郑东昊

(1.北京跟踪与通信技术研究所,北京 100095;2.北京理工大学 网络空间安全学院,北京 100081;3.中国西南电子技术研究所,成都610036)

0 引 言

电子干扰是长期困扰无线电测控、通信等领域的世界性难题,各国都长期集中精力开展对此问题的攻关。特别是近年来,共址平台上的装备越来越多,用频装备在空域、时域、频域维度之间的矛盾越来越突出。共址平台上的接收机具有非常高的接收灵敏度,其会受到来自共址平台其他装备如雷达、通信等大功率发射装备的影响[1-4]。当这些设备发射信号时,往往会导致高灵敏度接收机无法正常工作。因此,必须采取有效措施抑制该干扰。目前通常采用滤波器、限幅器等被动防护措施提供干扰防护,但该方式干扰抑制效果有限,特别是当干扰信号落在接收系统工作频带内时,滤波器也会抑制有用信号,造成有用信号的遗漏。另一种方式是采用自适应干扰对消的方式[5-7],即通过耦合器提取一部分发射信号作为参考信号,并对其进行时延、幅度和相位控制,使其与无线泄露来的干扰信号幅度相同、相位相反,然后将其与接收到干扰信号合成实现干扰对消。目前在该领域已有很多学者开展了研究,主要有两种干扰对消的方式：一是采用射频域的干扰对消[8-15]方式,即采用一些由可调器件组成的专用电路,并通过此电路在射频域重构从发射端耦合的射频参考信号,然后在接收端与干扰信号对消;二是在数字域对耦合的发射基带信号进行重构,使其与无线辐射的干扰信号在数字域能够对消[16-19]。

数字域的干扰对消不仅能够对消通过无线辐射进接收天线的干扰信号,而且还可以有效抑制发射放大器和接收放大器非线性引入的干扰。但由于该方式是在链路末端处理干扰信号,当应用于大功率干扰的场合,由于低噪声放大器(Low Noise Amplifier,LNA)的P-1较小,第一级LNA很容易饱和;或者即使LNA不饱和,由于AD的动态范围有限,大功率的干扰信号会超过AD的满刻度输入功率,导致数字采样失效。因此,在共址平台存在大功率干扰的场合,须在接收链路LNA之前采取射频干扰抑制措施,以有效抵御大功率干扰。

文献[8]和[10]提出了一种采用多抽头结构抑制射频干扰的方式,取得了不错的干扰抑制效果。两者首先都是通过人为配置多抽头各支路的时延,然后根据公式计算出各支路的控制权值。这种方式思路简单,但抽头个数较多,对相应数字控制模块的数据处理能力有较高的要求。这就导致射频电路的复杂度和成本较高,同时对数字控制模块里AD的要求也很高。

为解决上述问题,本文提出一种新型获取多抽头控制权值的方法。该方法不需要人为配置多抽头支路的时延,而是采用优化的方法获取全局最优的多抽头时延量,然后再计算出相应的权值。仿真结果表明,该方法具有所需抽头数目少、易于实现、性能优良的特点。

1 多抽头干扰对消系统模型

1.1 干扰对消原理

图1给出了共址平台射频干扰对消原理框图。x(t)代表从发射机耦合出的参考信号,x0(t)代表从发射天线辐射至接收天线的干扰信号,s(t)代表需要的接收信号。进入接收天线的信号可以表示为

图1 共址平台射频干扰对消原理框图Fig.1 Block diagram of the co-platform RF interference suppression system

d(t)=x0(t)+s(t)

(1)

在共址平台上,由于场地限制,装备数量较多且间隔较近,这就导致干扰信号的传播路径多且复杂,不仅有干扰装备天线与接收装备天线之间的直射路径,还有许多反射和散射路径。为便于分析,本文假设干扰信号经过M条无线传播路径到达接收机,则式(1)中的本地自干扰信号分量为

(2)

自干扰信道对应的频率响应可以表示为

(3)

式中：am代表第m条传播路径的衰减幅度;τm代表第m条传播路径的时延。

在干扰对消系统中,通过构建n条干扰对消通道(如图1所示),调整这些通道的时延、幅度和相位,使得经过这些干扰对消通道的干扰信号与经空间耦合的干扰信号等幅反相,从而达到干扰对消的目的。所构建的多抽头结构的频率响应为

(4)

式中：bn,φn,tn分别代表第n条干扰通道的幅度、相位和时延。将式(4)写为向量乘积的形式：

Hs(f)=XT(f)W

(5)

式中：T代表矩阵的转置;权矢量W定义为

(6)

频率f下的旋转因子矢量定义为

(7)

干扰抵消后的剩余自干扰信道频率响应可以表示为

Hr(f)=Hc(f)-Hs(f)=Hc(f)-XT(f)W

(8)

可以发现,求最小剩余自干扰信道频率响应的Hr(f)的过程转化为在X(f)给定之后(t1,t2,…,tn设为固定值),选择合适的W值即合适的相位φn和抽头增益bn,使得Hr(f)最小。

1.2 最优权值的获取

剩余自干扰信号功率谱密度为

Sr(f)=|Hr(f)|2S1(f)

(9)

式中：S1(f)代表发射信号的功率谱密度。假设近端发射机采用sinc(x)函数作为发射信号的成形脉冲函数,则本地发送射频信号的功率谱密度在信号带宽B内是平坦的。S1(f)可以表示为

(10)

则剩余自干扰信号的总功率如式(11)所示,H代表共轭转置。

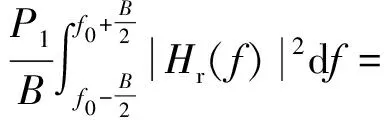
(11)

观察式(11)可以发现,Pr是W的二次函数。由于W是复向量,故当复向量梯度的实部和虚部均为0时,剩余干扰信号功率取得极值。对Pr求梯度可得

(12)

定义如下矩阵：

(13)

(14)

将R和Q表达式代入Pr表达式可得

(15)

(16)

(17)

将式(1)和式(5)代入上式,可得

(18)

rij=Bsinc[B(ti-tj)]ej2πf0(ti-tj)

(19)

式中：qn代表N×1矩阵中的元素;rij代表N×N矩阵中的元素。sinc(x)函数的定义如下：

Wopt=R-1Q

(20)

由式(20)可知,最优权值Wopt由R矩阵和Q矩阵决定,即由信号带宽B、工作频率f0、多抽头各支路时延tn、无线干扰信道的时延τm和幅度衰减am决定。在共址平台这一工作场景下,当干扰信号发射天线与接收装备天线固定不变时(波束也未扫描),信号带宽B、工作频率f0、无线干扰信道的时延τm和幅度衰减am可以认为是固定不变的,因此剩余可控的变量就剩下多抽头各支路时延tn,并且可以确定至少存在一组多抽头时延组合t1…tn使得对消后残余信号功率最小。

在实际实施过程中,采用延迟线来实现信号的时延。传统最优权值的获取方式[8-10]是通过人为配置一组时延组合t1…tn,即将每个支路的时延量设置为固定值,一般采用等差数列的形式设置每个支路的时延,然后通过公式(20)计算出对应的最优权值。该方式虽然简便易行,但所得到的权值并不一定是全局最优的,因为式(20)对应的问题不一定是凸优化问题。为此,本文提出一种基于优化算法获取最优权值的方式,首先设定多抽头的个数即时延组合的维度,然后基于优化算法,以最小残余信号功率为优化目标,以多抽头各支路时延为优化变量,得到一组对应的时延量组合,最后根据公式计算出对应的最佳权值。整个过程的流程如图2所示。

图2 多抽头射频干扰对消流程Fig.2 Flowchart of the multi-tap RF interference suppression system

所采用的优化算法有遗传算法(Genetic Algorithm,GA)、全局搜索算法(Global Search,GS)和多起点算法(MultiStart,MS)。GA是借鉴生物界进化规律演化而来的随机搜索方法,能够自适应地调整搜索方向,具有良好的全局搜索能力,不需要给定初始值。GS和MS两者均需要给出初始值,然后在此起点上产生若干个起始点,通过求解器寻找各个起始点附近的最优值,然后通过多次迭代比较,再从这些最优值里选出最优的。

社论属于政论文的范畴，因此，其中必定存在大量的论证性话语，论证的质量是关系到社论劝说效果成败的重要因素。社论的总体是躯干，而论证就是其骨骼，论证支撑着整个社论。因此，社论的论证必须符合逻辑，必须保证论证过程的严密性和科学性，而要达到逻辑的科学严密，作者必须运用元话语资源，将不同的命题组织起来，同时站在受众的立场，考虑受众的需求，发挥元话语目的性的导向功能，引导受众理解社论的内容，在此基础上完成社论的逻辑诉诸劝说功能的构建。

图3给出了采用3种方法求解最优值的收敛过程,其中GS算法和MS算法采用相同的初值。仿真参数为中心频率3 GHz,信号带宽120 MHz,采用修正S-V信道模型的CM1统计模型。

(a)GA算法

表1列出了3种优化算法的收敛次数,最终目标值和优化得到的最佳时延组合。很明显,采用GS算法的收敛过程最快,最终的目标值也最小。

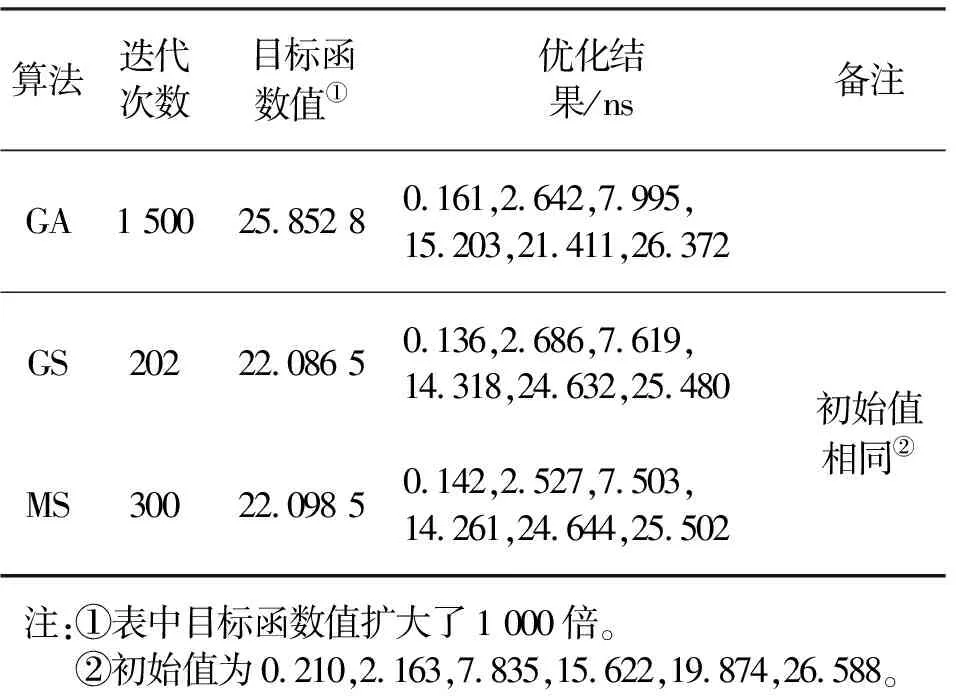
表1 3种搜索算法对比Tab.1 Comparisons among three methods

图4给出了3种优化算法得到的信道幅度响应对比曲线,可以看出,采用GS算法和MS算法的结果比较接近,两者均优于采用GA算法得到的结果,但GS算法的迭代次数较少,同时最终的目标值也稍小一些。因此,本文最终采用MS算法作为优化算法。

2 仿真与分析

根据前文分析,本文针对室内多径典型应用场景,基于Matlab开展仿真验证。仿真条件为载波频率2.4 GHz,信号带宽100 MHz,无线信道最大时延为26.2 ns。无线信道采用修正S-V信道模型的CM1统计模型,具体参数如表2所示。

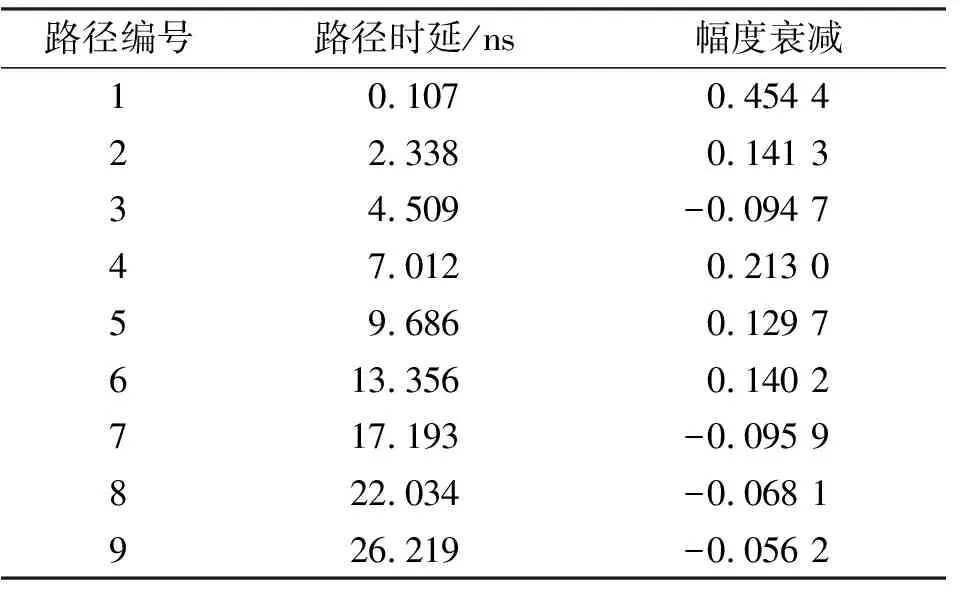
表2 无线信道参数Tab.2 Parameters of wireless channel

首先,设置多抽头的数目为6个,并设置多抽头的时延量初值,然后基于前文介绍的MS算法优化,得到一组时延量组合,然后根据式(18)得到多抽头支路的控制权值。同理,设置多抽头的数目为7个,重复上述过程,可得对应的最优控制权值。表3给出了初始值和优化得到的权值。

表3 多抽头的时延初值及优化后结果Tab.3 Initial and optimized values of the multi-tap circuits

图5给出了采用本文方法与文献[8]提出的干扰对消方法的仿真结果对比。可以看出,采用本文所提方法,抽头数目为6时,干扰抑制效果与对比文献的效果相当;当抽头数目为7时,本文方法效果远远优于对比文献方法的效果,但抽头数目却比对比文献方法抽头数目少。这表明,本文所提方法不仅干扰抑制效果好,而且可以减少抽头数目的个数,降低了射频电路的复杂度。同时,由于抽头数目的降低,其对相应的数字控制电路的要求也将降低。

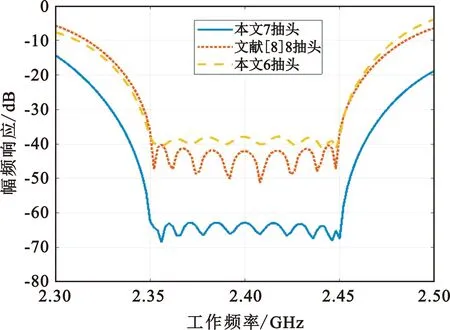
图5 本文所提方法与文献[8]干扰抑制效果对比Fig.5 Comparisons of the performance between the proposed method and Reference[8]

3 结束语

针对共址平台中大功率用频装备发射信号时会对其附近的高灵敏度接收机造成射频干扰的问题,本文提出了一种新型获取最优控制权值的方法,并给出了理论推导。Matlab仿真表明,采用本文方法的6抽头电路与传统方法的8抽头电路的干扰抑制性能相当,采用本文方法的7抽头电路比传统方法的8抽头电路的干扰抑制性能优大约25 dB,证明了本文方法具有抽头支路路少、干扰抑制性能高和对数字控制电路要求低的优点。

下一步将开展与数字域干扰对消相结合的混合干扰抑制系统研究。