基于IMM-KF算法改进的欺骗式干扰检测算法

陈世淼,倪淑燕,程凌峰,付琦玮,雷拓峰

(航天工程大学 a.研究生院;b.电子与光学工程系,北京 101416)

0 引 言

随着全球卫星导航系统(Global Navigation Satellite System,GNSS)在军事和民用领域中的广泛应用,GNSS的安全性和稳定性受到了极大的关注。由于导航信号强度弱、信号调制方式公开、部分导航数据可以预测等原因,GNSS极易受到欺骗式干扰[1-3],这对于导航系统是致命的。

欺骗式干扰是欺骗设备发出与真实导航信号相似的虚假导航信号,通过策略使得目标接收机将虚假导航信号误以为是真实导航信号,从而使目标接收机获取错误的定位、速度或时间信息。根据欺骗信号产生方式的不同,又可将欺骗式干扰分为生成式欺骗干扰和转发式欺骗干扰。

近年来已经出现了多种欺骗式干扰检测技术。基于单天线接收机信号处理的欺骗式干扰检测技术主要通过监测导航信号中载波相位[4]、码相位[5]和信号功率[6-7]等因素[8]的不合理跳变来实现欺骗干扰检测,可以作为接收机中的信号处理算法来实现。该方法对于简单欺骗式干扰具有很好的检测性能,是目前应用最多的欺骗干扰检测算法。基于信号空间信息的欺骗干扰检测技术利用欺骗干扰无法模拟真实导航信号的空间特征的特性,通过旋转单天线[9]、双天线[10-11]及多天线[12-13]技术进行信号的来向估计,从而实现欺骗干扰检测。该方法可有效检测来自同一方向的欺骗式干扰,但是对接收机天线要求较高。基于组合导航的欺骗干扰检测技术将GNSS与其他导航方式相结合,通过对比不同种导航方式的导航结果来进行欺骗干扰检测,常见的辅助导航方式有惯性导航、视觉导航、磁场导航、高精度时钟等。基于信号加密的欺骗干扰检测技术通过导航消息认证(Navigation Message Authentication,NMA)[14]、扩频码认证(Spreading Code Authentication,SCA)[15]和组合认证方法[16]对导航信号加密,使得导航信号难以被预测,并且接收机可以根据接收到的信号判断其完整性,从而更好地抵御欺骗攻击。基于机器学习的欺骗式干扰检测技术是一种通过机器学习对导航数据进行分析,并从中识别出欺骗式干扰的技术,目前常用的检测模型有卷积神经网络、K近邻算法、支持向量机、多层感知机、概率神经网络等,相比于传统的基于信号特性的欺骗式干扰检测算法有着更高的检测率。选择检测效果更好、计算量更小的模型是该检测算法的主要研究方向。

在当前欺骗式干扰检测方法中,绝大部分是基于接收机解算过程中的信息进行欺骗检测,在接收机上应用以上欺骗检测算法需要对原有的接收机进行重新设计,而已经出厂且不具有欺骗干扰检测功能的接收机将无法应用以上方法进行欺骗干扰检测。为此,文献[17-18]提出了一种基于基线长度观测量的欺骗干扰检测方法,通过多个接收机的导航解计算基线向量长度观测值,若基线向量长度观测值接近零则判定为被欺骗。该方法的检测性能与基线长度呈正比,在短基线情况下的检测性能较差。因此,本文引入交互多模型卡尔曼滤波(Interactive Multi-model Kalman Filtering,IMM-KF)算法,对多个接收机的定位解进行优化,降低误差对于基线长度观测值的影响,提高基线长度的解算精度,从而提高该检测方法在短基线和定位精度较差情况下的检测性能。

1 数学原理分析

根据欺骗信号产生装置的数目,可以将欺骗式干扰分为单站欺骗干扰和多站欺骗干扰。多站欺骗干扰中需要采用多个欺骗设备分别发射欺骗信号,这就要求对多个欺骗设备时钟同步,同时欺骗设备相对位置与导航卫星相对位置基本一致且能够协同发射欺骗信号,从而控制目标接收机接收到不同方位的欺骗信号。总的来说,多站欺骗式干扰实现的成本较高,技术与难度大,目前欺骗式干扰以单站为主。

下面以图1所示的单向欺骗式干扰为例,分析欺骗干扰对导航结果的影响。

图1 单方向欺骗式干扰示意Fig.1 Schematic diagram of spoofing in a single direction

在单站转发式欺骗干扰的情况下,欺骗设备接收到导航信号后通过一个发射机发送欺骗信号,若两接收机同时接收到欺骗信号,两接收机欺骗信号下的伪距单差为

(1)

式中：ds,r1为欺骗设备到接收机r1的距离;ds,r2为欺骗设备到接收机r2的距离。通过式(1)可以发现,欺骗信号中的不同卫星的站间单差均相等。

通过最小二乘法求导航解的过程中,将两接收机接收到的伪距表示为

(2)

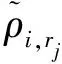
将式(1)代入式(2)可得

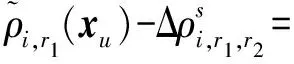
(3)

将伪距单差移到方程右侧可得

(4)

(5)

由此可以得出结论,在单站欺骗干扰环境下,被成功欺骗的两接收机根据欺骗信号求得的位置相同,而在两接收机接收真实导航信号的情况下,两接收机导航解的位置不同。所以,可以根据被欺骗的两接收机的基线长度观测值进行欺骗干扰检测。

2 欺骗检测算法

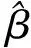
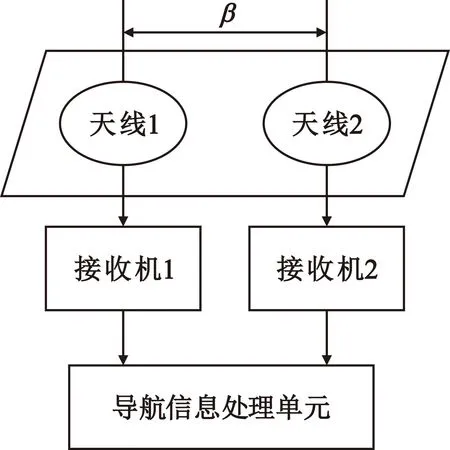
图2 欺骗信号检测系统模型Fig.2 Spoofing detection system model

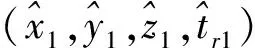
基线的长度观测量可表示为

(6)

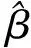
根据被欺骗和未被欺骗情况下基线长度的统计特性建立零假设和备选假设。在零假设情况下,构成基线的接收机未被欺骗,基线长度符合莱斯分布;在备选假设情况下,构成基线的接收机被欺骗,基线长度符合瑞利分布。基线长度在零假设和备选假设下的概率密度函数可以表示为

H0(未被欺骗)：

(7)

H1(被欺骗)：

(8)

式中：d为两接收机之间的距离;I0()是修正的0阶第一类贝塞尔函数;σpos为接收机定位的标准差。

基于基线长度观测量在零假设和备选假设下的概率密度函数,通过奈曼-皮尔逊(Neyman-Pearson)检验可以实现欺骗信号的检测。由于接收机定位的标准差受到位置精度强弱度(Position Dilution of Precision,PDOP)的影响,接收机的伪距测量误差σURE基本保持不变,所以令σpos=PDOP×σURE,根据检测过程中PDOP的变化调整检测阈值。

下面对检验性能与接收机距离和定位精度的关系进行分析。图3为接收机距离为2 m时受试者工作特征(Receiver Operation Characteristics,ROC)曲线与接收机定位精度的关系,可以看出随着接收机定位标准差σpos的增加,定位精度降低,欺骗检验的性能下降。原因是当两接收机距离固定时,σpos增加会导致零假设和备选假设下数据概率密度发散,数据重合概率增加,使得虚警概率增加,检测性能下降。图4为接收机定位精度σpos=2时ROC曲线与接收机距离的关系,可以看出随着接收机距离d的增加,欺骗检验的性能提升。原因是当两接收机定位性能确定时,d增加会导致零假设下数据的概率密度函数向x轴方向偏移,数据重合概率降低,使得虚警概率降低,检测性能提升。总之,当基线较短或接收机定位误差较大时,检测性能较差,因此引入交互式多模型对基线长度观测值进行优化。

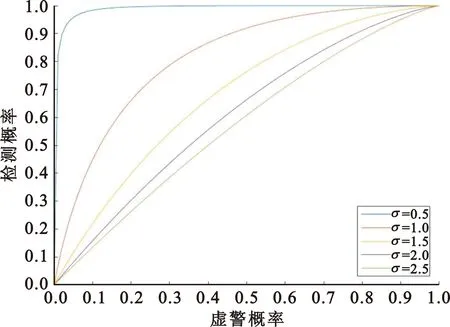
图3 d=2 m时的ROC曲线Fig.3 ROC curve at d=2 m

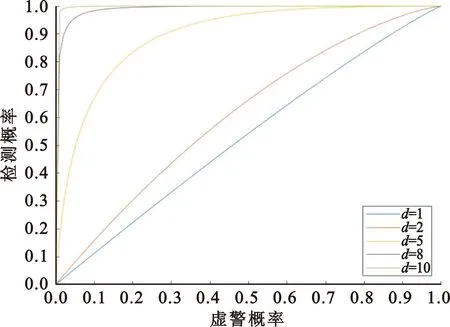
图4 σpos=2时的ROC曲线Fig.4 ROC curve at σpos=2

3 IMM-KF基线长度估计算法

考虑到欺骗检测设备一般应用于汽车、轮船、无人机等,采用单一运动模型进行滤波会降低鲁棒性,因此采用CV(Constant Velocity)运动模型和CT(Constant Turn)运动模型的IMM算法来描述系统的运动。IMM算法用多个运动模型来描述不断变化的系统,每一个模型对应一个滤波算法,根据模型概率融合多个模型的结果,作为每一个时刻的输出[19]。用于欺骗检测的两个接收机天线固定于应用载体,两个天线的位置不同,运动状态与应用载体相同,因此设置运动模型状态量为Xk=(xk,1,yk,1,zk,1,xk,2,yk,2,zk,2,vx,k,vy,k,vz,k)T。其中,(xk,1,yk,1,zk,1,xk,2,yk,2,zk,2)T为两个天线在k时刻的位置,(vx,k,vy,k,vz,k)T为应用载体在k时刻的速度。对文献[20]中卡尔曼滤波模型扩维可以得到本文的卡尔曼滤波模型。

建立欺骗检测设备的运动状态方程为

Xk=FXk-1+Gwk-1

(9)

式中：wk代表过程噪声;F和G分别代表状态转移矩阵和噪声驱动矩阵,定义分别为

(10)

(11)

(12)

式中：T是采样时间间隔。

建立欺骗设备的量测方程为

Zk=HXk+vk

(13)

式中：观测量Zk=[xk,1,yk,1,zk,1,xk,2,yk,2,zk,2]T;vk是量测噪声;H为量测矩阵,表示为

(14)

基于状态方程和量测方程,将卡尔曼滤波应用于提高估计精度的算法(IMM-KF算法)过程如下：

输入：不同模型在k-1时刻的状态估计量Xi,k-1,k-1时刻的状态协方差矩阵Pi,k-1,模型概率μi,k-1,k时刻的观测量Zk。

输出：不同模型在k时刻的状态估计量Xi,k,k时刻的状态协方差矩阵Pi,k,模型概率μi,k,融合输出的XIMM,kPIMM,k。

步骤1 交互输入。将上一时刻中CV模型和CT模型的输出值基于马尔可夫矩阵交互来得到新的滤波状态估计量和协方差矩阵：

(15)

(16)

(17)

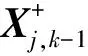
步骤2 CV模型和CT模型卡尔曼滤波器滤波。根据上一时刻的CV模型状态估计量和状态协方差矩阵进行滤波,得到当前时刻的状态估计量和状态协方差矩阵：

(18)

(19)

(20)

(21)

(22)

计算CV模型估计的残差和残差协方差矩阵：

ECV,k=Zk-HFCVXCV,k-1

(23)

(24)

对于CT模型重复执行上述流程。

步骤3 模型概率更新。计算各模型似然函数：

(25)

更新模型概率：

(26)

步骤4 输出融合后的状态估计量和状态协方差矩阵：

XIMM,k=XCV,kμCV,k+XCT,kμCT,k

(27)

PIMM,k=μCV,k[PCV,k+(XCV,k-XIMM,k)(XCV,k-XIMM,k)T]+
μCT,k[PCT,k+(XCT,k-XIMM,k)(XCT,k-XIMM,k)T]

(28)

4 性能仿真

4.1 仿真环境设置

仿真实验过程中真实和欺骗的导航中频信号由图5所示的导航信号模拟器产生,使用软件定义的导航接收机对中频信号进行解算,根据解算结果运行本文设计的算法,实现欺骗干扰检测。导航信号模拟器根据两个接收机的真实轨迹产生的导航信号作为真实信号;导航信号模拟器根据欺骗轨迹产生导航信号作为欺骗信号,在软件接收机根据伪距求解的过程中,其中一个接收机的每一个伪距都同时增加固定值,来模拟单站欺骗干扰导致的两个接收机之间的伪距差异。

图5 导航信号模拟器Fig.5 Navigation signal simulator

仿真过程中参数设置如表1所示。图6为真实导航信号和欺骗信号的真实轨迹,欺骗装置以5 m/s的速度向北方向前进,在第30 s施加欺骗信号,其中50～70 s以3 °/s的速度右转弯,80～100 s以3 °/s的速度左转弯,其余时间保持直线运动。仿真过程中PDOP值为1.603 2。

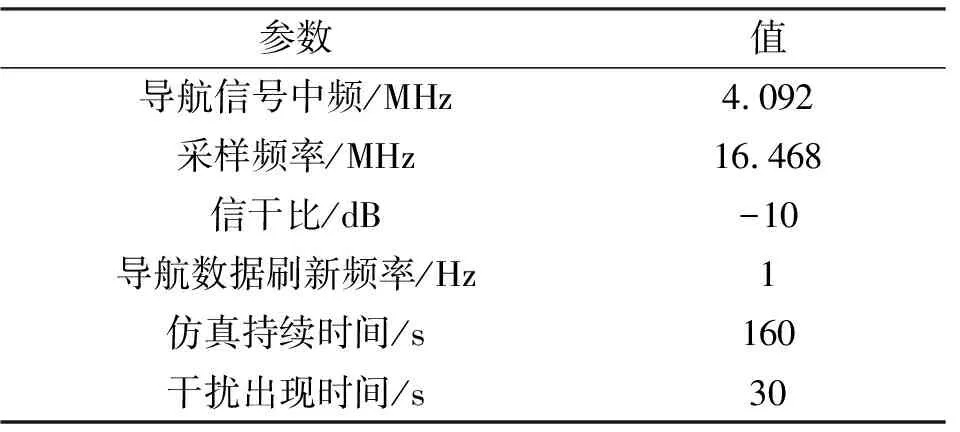
表1 仿真参数设置Tab.1 Simulation parameter settings

图6 轨迹Fig.6 Trajectory

4.2 仿真结果及分析

图7展示了接收机的基线长度和伪距观测精度取值不同时,基线长度观测值的变化。对比不同仿真结果可以得出如下结论：

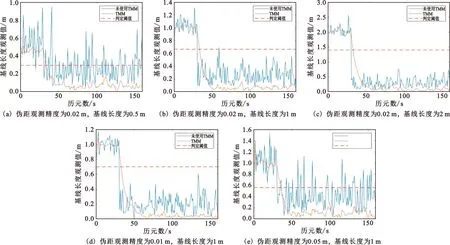
图7 不同情况下基线长度观测值Fig.7 Baseline length observations under different conditions

1)基线长度的增加和伪距观测精度的降低都会导致检测精度的下降,这与ROC曲线仿真结果一致;

2)经过IMM-KF算法处理后的基线长度估计精度明显优于原始值,因此采用IMM-KF算法会显著提高欺骗检测性能,特别是基线长度取值较小或伪距观测精度较差的情况下;

3)当伪距观测精度为0.02 m时,传统方法需要保证基线长度大于1 m才能保持较好的检测性能,本文所提出方法能够在基线长度为0.5 m时仍能保持较好的检测性能。

为了更好地评估检测性能,进行了1 000次蒙特卡罗仿真,图8是基线长度和伪距观测精度不同时的检测概率、虚警概率和检测响应时间。从图8可以看出,即使是在基线长度为0.5 m、伪距观测精度为0.1 m的情况下,经过IMM-KF算法改进的欺骗干扰检测算法仍然能达到86%的检测成功率,此时虚警概率约为0.39%,检测响应所需数据约为7.3组。当基线长度增加或者伪距观测精度提高时,算法的检测性能会进一步得到提升。在基线长度为0.5 m、伪距观测精度为0.1 m的情况下,未加入IMM-KF的传统检测算法的检测成功率仅为10%,此时传统检测算法基本失去欺骗干扰检测能力。

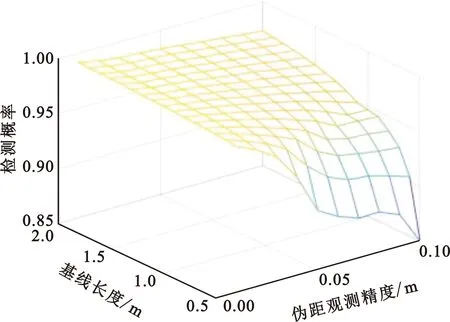
(a)检测概率

5 结束语

本文在分析基于基线长度的欺骗检测方法原理的基础上,考虑到检测算法在短基线和定位精度差的情况下检测效率低的问题,利用IMM-KF算法来提高基线长度观测值的估计精度,提高了检测算法的鲁棒性。通过仿真发现,IMM-KF算法的应用可有效提高欺骗检测算法在短基线和低定位精度情况下的检测性能,即使在基线长度为0.5 m、伪距观测精度为0.1 m的情况下,经过IMM-KF算法改进的欺骗检测算法仍然能达到86%的检测成功率,此时传统方法检测成功率仅为10%。

未来将针对多个接收机的多种组合方式、不同优化算法下的欺骗算法检测性能展开研究。