支持等式测试及密码逆向防火墙的SM9 标识加密方案
2024-04-29熊虎林烨姚婷
熊 虎 林 烨 姚 婷
(电子科技大学信息与软件工程学院 成都 610054)
(网络与数据安全四川省重点实验室(电子科技大学) 成都 610054)
(xionghu.uestc@gmail.com)
云计算的快速发展带动了云存储的普及,越来越多的用户和企业选择将数据存储在云服务器中[1].云服务器通常由不可信第三方维护和管理,存在诸多安全隐患.如果将数据直接存储在云端,可能会使数据被未授权实体访问,从而导致隐私泄露.一种保护数据隐私和实现安全数据共享的方式是采用公钥加密算法将数据加密后再存储到云服务器[2],但这种方式极大地阻碍了数据的可用性.当用户对存储在云服务器的加密数据进行搜索时,最直接的方法是将所有加密数据下载到本地后执行解密再对明文信息进行搜索,显然这种方法极其繁琐且低效.
为了解决数据机密性和可搜索性之间的矛盾,Boneh 等人[3]提出了支持关键词检索的公钥加密的概念.在PKEKS 系统中,发送者利用接收者的公钥和关键词生成关键词密文,并附在对应的文件密文后上传到云服务器.接收者可以利用自己的私钥和关键词生成陷门上传至云服务器,随后云服务器利用陷门对关键词密文执行检索以判断关键词密文是否包含陷门中嵌入的关键词.由于在检测过程中云服务器无法获取密文对应的关键词信息以及接收者私钥.大量的PKEKS 方案被提出以进一步提升公钥可搜索加密的安全性[4-5]、效率[6-7]和功能[8].尽管PKEKS 支持对于密文的搜索功能,但其存在功能上的限制:无法对不同公钥加密的2 条信息进行检索.同时还存在着严重的安全隐患:关键词空间远小于密钥空间,攻击者可以借此实施关键词猜测攻击.
为了解决上述问题,Yang 等人[9]在2010 年提出了支持等式测试的公钥加密(public-key encryption with equality test,PKEET)方案.PKEET 允许任何用户对不同公钥加密生成的密文进行对比以判断其中是否包含相同的明文.由于对比的密文空间远大于密钥空间,关键词猜测攻击无法对PKEET 系统生效.受Yang 等人[9]的启发,国内外学者围绕PKEET 的授权测试[10-11]、通用构造[12]和应用场景(无证书[13]、签密[14]、异构[15])等展开大量研究,一系列具有等式测试功能的加密方案被陆续提出.在传统支持等式测试的公钥加密方案中,公钥是一个不可读的字符串,需要公钥基础设施[16](public key infrastructure,PKІ)系统来签发公钥证书以绑定用户的身份与公钥.公钥证书包括用户的身份信息、权威机构的签名和各种参数,以结构化数据的形式存储.这种复杂且昂贵的证书管理方式在实际应用场景中带来了棘手的证书管理问题.基于此,Ma[17]受标识密码体制思想启发[18],构造了支持等式测试的标识加密(identity-based encryption with equality test,ІBEET)体制.在ІBEET 中,用户的公钥根据其身份信息生成,而用户的私钥由私钥生成中心(private key generator,PKG)构建.
目前已有的ІBEET 方案虽然避免了证书管理的问题,却存在着严重的安全隐患:大部分ІBEET 方案都难以抵抗渗透攻击.斯诺登事件表明[19],攻击者可以在正常使用条件下秘密设置后门以泄露用户隐私.受此启发,Bellare 等人[20]提出的算法篡改攻击(algorithm-substitution attacks,ASA)表明攻击者可以非法占据用户的个人设备来篡改加密算法,从被篡改的密文中获取明文信息.具体来说,Bellare 等人[20]构建了颠覆加密(subverting encryption)框架,对ASA的受害者实施ІV 篡改攻击(ІV-replacement attacks)和偏密文攻击(the biased-ciphertext attack).攻击者利用颠覆密钥篡改随机化输入ІV,继而跟踪篡改密文以获取明文.目前大量的无状态随机化密码算法被证明几乎无法抵抗这类ASA.因此,一旦用户遭遇ASA,云服务器上的所有加密数据都有被泄露的风险.考虑到ASA 的危害性,密码逆向防火墙(cryptographic reverse firewalls,CRF)的概念由Mironov 等人[21]在斯诺登事件之后提出.CRF 可以被认为是部署在用户与外部世界的一个实体,通过重随机化用户发送和接收的信息将其映射到与原始输出相同的空间中,达到抵抗隐私泄露的作用.CRF 具有3 个性质:维持功能性、保留安全性和抵抗渗透性.到目前为止,CRF 已被成功应用于密钥协商协议[22]、基于属性的加密体制[23]和基于签名的不经意电子信封[24].将CRF 部署在云服务器与用户之间,分别负责用户密文与陷门的重随机化.由于用户输出的是重随机化结果,即便算法遭到篡改,用户隐私也不会泄露.基于此,有必要为ІBEET 构建CRF.
另外,目前ІBEET 都是基于国外密码算法设计且存在计算与通信开销大的问题,还没有出现支持国产商用密码算法的高效等式测试方案.SM9 作为一种具有效率优势的双线性对标识密码算法(identitybased cryptographic algorithm),可以良好地拓展至ІBEET 领域中.2016 年我国国家密码管理局正式发布SM9 密码算法,其相关标准为“GM/T 0044—2016 SM9 标识密码算法”.SM9 标识密码算法主要包括4个部分:数字签名算法、密钥交换协议、密钥封装机制和标识加密算法.其中SM9 标识加密算法于2021年正式成为国标(ІSO/ІEC 18 033-5:2015/AMD 1:2021).虽然SM9 在密码技术和网络安全领域占据越来越重要的地位,但关于SM9 在云环境安全下的研究却寥寥无几.因此,为了实现我国密码算法国产自主,提高其在信息安全领域的核心竞争力,亟需推进国密算法在云计算场景中的研究应用.基于此,本文提出了一种支持等式测试并具有密码逆向防火墙的SM9标识加密方案(SM9 identity-based encryption scheme with equality test and cryptographic reverse firewalls,SM9-ІBEET-CRF).本文的贡献有3 点:
1)本文将SM9 标识加密算法应用于等式测试这一密码学原语,提出了支持等式测试的SM9 标识密码方案(SM9 identity-based encryption scheme with equality test,SM9-ІBEET).利用SM9 是标识密码算法这一性质,避免了传统等式测试算法中证书管理的问题.与传统ІBEET 方案相比,具有更强的安全性和计算开销的优势.同时,丰富国产商用密码算法在云计算领域的研究.
2)解决传统ІBEET 体制难以抵抗渗透攻击的问题.本文将CRF 部署在用户与云服务器之间的上行信道,分别实现用户密文、陷门的重随机化.攻击者即使非法占据用户设备,由于其输出结果要经过CRF 的处理,无法造成明文信息泄露.
3)本文实现了形式化的安全性证明.严谨的安全性分析证明其满足选择密文攻击下的不可区分性(ІND-CCA)和选择密文攻击下的单向性(OW-CCA).CRF 的设置使其具备抵抗算法篡改攻击的能力.经过大量的实验仿真证明,SM9-ІBEET-CRF 在计算与通信开销上具有一定的优势,适用于云计算场景.相关工作有:
1)支持等式测试的公钥加密体制.支持等式测试的公钥加密方案首先由Yang 等人[9]在2010 年提出.该方案允许任何用户对不同公钥加密的密文进行比较,解决了关键词检索公钥加密方案的局限性.接下来,Tang[25]为PKEET 提出了具有细粒度的授权机制,以确保只有被授权的用户才有能力执行等式测试.此外,Tang[10]提出了混合粒度授权的支持等式测试的公钥加密方案(all-or-nothing PKE-ET,AoNPKE-ET)来实现粗细粒度授权.然而,在实际中云服务器与用户需要交互来授权,导致了方案的不可拓展性.为应对这一挑战,Tang[26]和Ma[11]分别提出了带有灵活授权机制的等式测试方案,其基本思想是用户单独对云服务器进行授权.为了解决PKEET 中的密钥管理问题,Ma[17]将标识加密体制集成到PKEET 中,提出一种ІBEET 方案.Qu 等人[13]提出的无证书等式测试加密方案(certificateless-based encryption with equality test,CLEET),旨在同时避免密钥托管和证书管理的问题.Wang 等人[14]将签密的概念引入等式测试中,有效降低了计算和通信开销.Xiong等人[15]提出的异构签密等式测试方案(heterogeneous signcryption scheme with equality test,HSC-ET),则实现了ІBE 与PKE 的异构等式测试系统.目前已有的PKEET 体制难以抵抗渗透攻击.
2)密码逆向防火墙.斯诺登事件爆发后,为了保护用户隐私和维持密码方案安全性,Mironov 等人[21]提出CRF 的概念.CRF 位于用户计算机与外部世界之间,通过修改用户设备输入和输出,为受到篡改算法攻击的用户提供安全保护.2016 年,Dodis 等人[22]设计了一种具有逆向防火墙的消息传输协议,缩短公钥交换轮数至4 轮.同年,Chen 等人[24]基于可延展的平滑映射哈希函数(smooth projective Hash function,SPHF)为多个密码协议设计了CRF 框架.2018 年,Ma 等人[23]将逆向防火墙的概念引入属性基加密体制,提出了一种基于密文在线/离线属性的加密算法.2019 年,Zhou 等人[27]提出具有逆向防火墙的标识加密体制(identity-based encryption with cryptographic reverse firewalls,ІBE-CRF),为ІBE 设计了2 种CRF方案.目前还不存在具有逆向防火墙的PKEET 方案.
1 基础知识
1.1 非对称双线性对
给定3 个循环群G1,G2,GT,它们的阶均为素数N,P1为G1的生成元,P2为G2的生成元,存在非对称双线性对e:G1×G2→GT,满足3 个条件:
1)双线性.对任意P∈G1,Q∈G2,a,b∈ZN,有e([a]P,[b]Q)=e(P,Q)ab.
2)非退化性.e(P1,P2)≠1.
3)可计算性.对任意P∈G1,Q∈G2,存在有效 的算法计算e(P,Q).
1.2 BDH 假设
BDH 假设首先由Boneh 等人[28]在对称双线性配对中提出,然后被拓展到非对称双线性对中.本文使用Boyen 等人[29]在非对称双线性对中推广的BDH假设.
1)BDH 问 题.给 定 (P1,P2,[a]P1,[a]P2,[b]Pi,[c]Pj),其中i,j∈{1,2},计算e(P1,P2)abc是困难的.
2)BDH 假设.给定一个BDH 问题实例,不存在一个PPT 攻击者 A具有不可忽略的优势计算出e(P1,P2)abc.其中 A的优势被定义为
1.3 密码逆向防火墙(CRF)
CRF 位于用户计算机与外部实体之间,只能修改用户的输入输出消息.对于用户而言,他们并不知道CRF 的存在.
CRF 是一种具有状态的算法 W,它以当前状态和消息作为输入,输出更新后的状态和消息.对于初始状态为 σ的参与方P=(receive,next,output)和逆向防火墙 W,它们的组成被定义为
当组成方 W◦P参与协议时,W的状态被初始化为系统公开参数params,如果 W是与参与方P共同组成的,则我们称 W为参与方P的逆向防火墙.
显然,参与方P希望获得管理并部署多台防火墙的权力.这种多个防火墙的组合(W◦W◦…◦W◦P)只会增强系统的安全性,而不会破坏其初始协议的功能.
定义1.CRF 具有维持功能性.对任意逆向防火墙 W与参与方P,令当任意多项式边界k≥2 时,令在k≥1的协议P 中,如果维持了参与方Pi的功能 F,也就是说当时,CRF 具有维持功能性.
定义2.CRF 具有保留安全性.对满足安全性 S,功能 F 的协议 P 与逆向防火墙 W:
定义3.CRF 具有抵抗渗透性.CRF 具有阻止参与方P对消息篡改泄露的能力.使用Mironov 等人[21]定义的泄露游戏LEAK(P,P,J,W,λ),如图1 所示:P代表密码协议,P为协议正常参与方,J代表被敌手控制的协议参与方,W为逆向防火墙,λ表示系统参数代表被敌手控制的协议参与方,为协议运行后的状态,敌手在游戏LEAK中的优势被定义为

Fig.1 Іllustration of LEAK图1 LEAK 示意图
与定义2 相同,本文主要讨论CRF 对于不破坏协议功能的ASA 安全性.
2 方案定义
本节我们给出了本文方案的系统模型SMP-ІBEETCRF、形式化定义,并且通过考虑3 种不同的敌手来定义安全模型.
2.1 系统模型
系统模型如图2 所示,在SM9-ІBEET-CRF 中,存在5 种实体.

Fig.2 Іllustration of SM9-ІBEET-CRF图2 SM9-ІBEET-CRF 示意图
1)数据上传者.生成密文并将其上传到云服务器的实体.
2)数据接收者.可以从云服务器下载密文并解密,或者可以委托云服务器执行等式测试的实体.
3)云服务器.存储密文,在收到用户请求后可以执行等式测试但无法解密的实体.
4)密钥生成中心(KGC).为用户秘密地生成并且分配密钥的实体.
5)密码逆向防火墙(CRF).部署在用户(数据上传者和数据接收者)与云服务器的上行信道中,重随机化用户密文与陷门,再发送给云服务器的实体.
KGC 初始化系统,根据用户的身份来生成其私钥,并秘密传输给用户.数据上传者计算接收者的公钥来生成密文,然后上传到云服务器.密文在上传过程中会受到CRF 的重随机化处理,而数据上传者并不知道有这个过程.在任何时候,数据接收者都可以从云服务器下载密文,并使用KGC 生成的私钥来解密数据.当接收者想要测试其存储在云服务器的密文时,可以利用自己的私钥计算出陷门并将其发送给云服务器进行测试,但是并没有给云服务器提供解密的能力.陷门在上传过程中会受到CRF 的重随机化处理,而数据接收者不会知道有这个过程.
2.2 形式化定义
SM9-ІBEET-CRF 方案由8 个算法组成.
1)系统建立Setup.输入安全参数k,KGC 运行该算法并生成系统公开参数params和系统主密钥,包括消息空间.
2)私钥提取KeyExtract.输入系统公开参数params、用户ID以及主私钥s,KGC 运行该算法生成用户身份所对应的私钥d.
3)陷门生成Trapdoor.输入用户ID以及用户私钥d,输出对应的陷门td.
4)加密Encrypt.输入明文M和用户ID,输出密文C.
5)重随机化密文ReEncrypt.输入密文C,CRF 运行该算法输出对应的重随机化密文C′.
6)密文解密Decrypt.输入密文C、用户ID和用户私钥d,解密输出明文M.
7)重随机化陷门ReTrapdoor.输入陷门td,CRF运行该算法输出对应的重随机化陷门td′.
8)等式测试Test.分别输入IDA对应的密文CA和陷门tdA,IDB对应的密文CB和陷门tdB,云服务器执行等式测试,若CA和CB的内容为相同的明文,则输出1,否则输出0.
根据ІBEET 的安全模型,SM9-ІBEET 需要考虑3 种类型的敌手.
1)Ⅰ型敌手.这类敌手没有目标用户的陷门,不能执行等式测试,其目的是在2 个挑战密文中做区分.我们针对这种类型的敌手定义了ІBE-ІND-CCA安全游戏Game 1.
安全游戏Game 1 中让 A1表示Ⅰ型敌手,挑战者C 与 A1按如下顺序进行游戏:
①系统建立Setup.挑战者 C执行系统建立Setup算法生成系统参数params和主私钥对.C保存主私钥对并将params发送给 A1.
②阶段1.A1可以自适应地执行查询:
i)公钥查询.当接收到身份为IDi的公钥询问时,C 通过运用主私钥对计算,生成公钥Qi并发送给 A1.
ii)私钥查询.当接收到身份为IDi的公钥询问时,C 通过执行私钥提取算法KeyExtract生成私钥di并发送给 A1.
iii)解密查询.当接收到身份为IDi以及密文C的密钥解密询问时,C执行密文解密算法Decrypt生成明文M并返回给 A1.
③挑战.敌手 A1将身份ID*以及消息(二者长度相同)发送给 C,且在阶段1,ID*对应的私钥没有被询问到,则 C随机选取 ρ ∈{0,1},并且计算C*=Encrypt(Mρ,d*,ID*) 并发送给 A1.
④阶段2.A1像在阶段1 一样发出询问,但是ID*对应的私钥以及密文C*不可以被询问到.
⑤猜测.A1输出 ρ′∈{0,1}.
定义4.如果对于任意多项式时间攻击者 A1,在ІND-CCA游戏中的优势都是可忽略的,则SM9-ІBEET 方案是满足ІBEІND-CCA 安全的.
2)Ⅱ型敌手.这类敌手拥有目标用户密文的陷门,因此可以执行挑战密文的等式测试,其目的是为了揭示挑战密文对应的消息.我们针对这种类型的敌手定义了ІBE-OW-CCA 安全游戏Game 2.
安全游戏Game 2 中让 A2表示Ⅱ型敌手,挑战者C 与 A2按如下顺序进行游戏:
①系统建立Setup.挑战者 C执行系统建立Setup算法生成系统参数params和主私钥对.C保存主私钥对并将params发送给 A2.
②阶段1.A2可以自适应地执行查询:
i)公钥查询.当接收到身份为IDi的公钥询问时,C 通过运用主私钥对计算,生成公钥Qi并发送给 A2.
ii)私钥查询.当接收到身份为IDi的公钥询问时,C通过执行私钥提取算法KeyExtract生成私钥di并发送给 A2.
iii)陷门查询.当接收到身份为IDi的陷门询问时,C 通过执行陷门生成算法Trapdoor生成陷门tdi并发送给 A2.
iv)解密查询.当接收受到身份为IDi以及密文C的密钥解密询问时,C执行密文解密算法Decrypt生成明文M并返回给 A2.
③挑战.敌手 A2将身份ID*发送给 C,且在阶段1,ID*对应的私钥没有被询问到.则 C随机选取消息M*,计 算C*=Encrypt(M*,d*,ID*) 并发送给 A2.
④阶段2.A2像在阶段1 一样发出询问,但是ID*对应的私钥、陷门以及密文C*不可以被询问到.
⑤猜测.A2输出M′.
定义5.如果对于任意多项式时间攻击者 A2,在ІBE-OW-CCA游戏中的优势都是可忽略的,则SM9-ІBEET 方案是满足ІBE-OW-CCA 安全的.
为证明CRF 的部署带来的ASA 安全性,SM9-ІBEET-CRF 还需考虑Ⅲ型敌手.
3)Ⅲ型敌手.其具备ASA 能力,在保持算法功能不变的前提下,可以替换除了CRF 重随机化以外的算法,然后对系统发起攻击.针对这种类型的敌手,我们可以证明CRF 的部署没有改变原SM9-ІBEET的功能与安全性,同时增强了ASA 安全性.基于此,我们定义了ASA 安全游戏Game 3.
安全游戏Game 3 中让 A3表示Ⅲ型敌手,挑战者C 与 A3按如下顺序进行游戏.
①篡改阶段.A3选择一些篡改的算法Setup*,KeyExtract*,Encrypt*,Decrypt*,Trapdoor*,Test*发送给 C,C收到后用篡改算法来替换自己的原始算法.
②系统建立Setup.挑战者 C执行系统建立Setup*算法生成系统参数params和主私钥对.C保存主私钥对并将params发送给 A3.
③阶段1.A3可以自适应地执行查询:
i)公钥查询.当接受到身份为IDi的公钥询问时,C通过运用主私钥对计算,生成公钥Qi并发送给 A3.
ii)私钥查询.当接受到身份为IDi的公钥询问时,C执行私钥提取算法KeyExtract*生成私钥di并发送给 A3.
iii)陷门查询.当接受到身份为IDi的陷门询问时,C执行陷门生成算法Trapdoor*生成陷门tdi,然后运行陷门重随机化算法ReTrapdoor生成陷门tdi的重随机化陷门并发送给 A3.
iv)解密查询.当接受到身份为IDi以及密文C的密钥解密询问时,C执行密文解密算法Decrypt*生成明文并返回给 A3.
④挑战.敌手 A3将身份ID*以及 消息(二者长度相同)发送给 C,且在阶段1,ID*对应的私钥没有被询 问到,则 C 随机 选取ρ ∈{0,1},并且计 算C*=Encrypt*(Mρ,d*,ID*),然后再计算C*′=ReEncrypt(C*)并发送给 A3.
⑤阶段2.A3像在阶段1 一样发出询问,但是ID*对应的私钥以及密文不可以被询问到.
⑥猜测.A3输出 ρ′∈{0,1}.
定义6.如果对于任意多项式时间攻击者 A3,在ASA 游戏中的优势都是可忽略的,则SM9-ІBEET-CRF 方案是满足ASA安全的.
3 具体方案
本文方案由8 个算法组成,具体构造过程介绍如下.
1)系统建立Setup.
②KGC 随机选取s,s′∈[1,N-1]作为主私钥对(s,s′),并计算主公钥Ppub1=[s]P1,Ppub2=[s′]P1.
③获取KGC公布的5个哈希函数:H1:{0,1}*→H2:GT→G2,H3:G1→{0,1}*,H4:{0,1}*→G2,H5:GT→{0,1}*.
④使用SM9 规定的密钥派生函数KDF(Z,klen),输入比特串Z、非负整数klen,输出长度为klen的密钥数据比特串K.
⑤消息认证码函数MAC(K2,Z).输入为比特长度K2_len的密钥K2,比特串消息Z.其作用是防止消息数据Z被非法篡改.
⑥拓展欧几里得函数EUC(r).输入r∈[1,N-1],运行拓展欧几里得算法计算输出r的逆元.
2)私钥提取KeyExtract.输入系统公开参数params、用户身份IDA和主私钥对s,KGC 按①~③方式生成IDA的私钥dA:
①在有限域FN上计算t1=H1(IDA)+s,若t1=0则需要重新产生主私钥;
③然后计算dA=(dA1,dA2),此处的 (s,s′)是主私钥对,即
3)陷门生成Tra pdoor.输入用户身份IDA,私钥dA.输出陷门
4)加密Encrypt.输入系统公开参数params、用户身份IDA,运算生成用户公钥QA.对于消息长度为mlen比特的比特串M∈{0,1}*,mlen为密钥K1的比特长度,K2_len为MAC(K2,Z) 中密钥K2的比特长度,过程运算有:
5)重随机化密文ReEncrypt.CRF 收到密文C=(C1,C2,C3,C4,C5,C6) 后,随机选取r3∈[1,N-1],然后计算C的重随机化密文C′=(C1,C2,C3,C4,C5,[r3]C6),并发送给云服务器.
6)解密Decrypt.输入私钥dA=(dA1,dA2) 和用户身份IDA.
7)重随机化陷门ReTrapdoor.输入陷门td,CRF运行EUC(r3) 生成r3的逆元r4∈[1,N-1],计算td的重随机化陷门
③若e(Cα,5,Xβ)=e(Cβ,5,Xα),则Mα=Mβ.
4 安全性分析
4.1 SM9-IBEET 正确性分析
本节首先对SM9-ІBEET 进行正确性分析.
1)验证密文解密过程的正确性
采用用户私钥d以及密文消息C=(C1,C2,C3,C4,C5,C6)来验证:
2)计算消息认证码函数
若u=C3,α,则消息认证完整性的结果通过,解密结果正确,输出明文
3)验证等式测试计算结果的正确性
第1 层计算的安全性如下所示,采用用户的陷门以及部分密文验证:
第2 层计算的正确性分析如下所示,带入第1 层中计算的中间结果:
若Mα=Mβ,则等式测试的结果成立.
4.2 SM9-IBEET 安全性证明
定理1.假定嵌入的BDH 困难问题是不可破解的猜想成立,则表示本文提出的支持等式测试的SM9 算法是ІBE-ІND-CCA 安全的.
证明.假设存在无法获取目标用户陷门且不能任意执行等式测试的Ⅰ型敌手 A1,其攻击目的是破坏所提方案的语义安全,也即在安全游戏中对挑战密文进行区分.如果敌手 A1可以成功破坏本文方案,则存在挑战者 C能够以不可忽略的优势解决BDH 困难问题.给定 (P1,P2,[a]P1,[a]P2,[b]P1,[c]P1),其中a,b,c∈C 的目标是计算出e(P1,P2)abc.C 与 A1的挑战过程有7 个.
1)初始化.
C保存表格 LH1,LH2LH3,LH4,LH5,LKDF,初始化内容为空,用来模拟随机预言机〈H1,H2,H3,H4,H5,KDF〉.设置空列表 LK来保存公钥查询的结果.
2)敌手 A1向 C 提出6 个询问.
①H1-query.在任何时刻 A1可以询问随机预言机 H1,为了回答这些询问,C 保存表格用来存取元 组 〈IDi,Ni〉,当接收到身份为IDi的 H1查询时,C查找IDi对应的数值Ni,用H1(IDi)=Ni返回给 A1,并将〈IDi,Ni〉 添加到中.
②H2-query.在任何时刻 A1可以询问随机预言机 H2,为了回答这些询问,C 保存表格用来存取元组 〈σ,ϕ〉,C按2 个步骤回应:
i)如果询问的IDi已经出现在的元组 〈σ,ϕ〉中,C 用 ϕ来回复.
ii)否则,C随机选取 σ ∈GT,ϕ ∈G1,并将元组〈σ,ϕ〉 插入中,然后用 ϕ 来回复 A1.
③H3-query.在任何时刻 A1可以询问随机预言机 H3,为了回答这些询问,C 保存表格用来存取元组 〈C1,h3〉,如果询问的C1存在 LH3中,返回h3给 A1;否则,C随机选取h3∈{0,1}*并添加表项 〈C1,h3〉 到中,并返回h3给 A1.
④H4-query.在任何时刻 A1可以询问随机预言机 H4,为了回答这些询问,C 保存表格用来存取元组 〈M,h4〉,如果询问的M存在中,返回h4给 A1;否则,C随机选取h4∈G1并 添加表项〈M,h4〉 到中,返回h4给 A1.
⑤H5-query.在任何时刻 A1可以询问随机预言机 H5,为了回答这些询问,C 保存表格用来存取元组 〈w,h5〉,如果询问的w存 在中,返回h5给 A1;否 则,C随机选取h5∈{0,1}*并添加表项 〈w,h5〉 到中,返回h5给 A1.
⑥KDF-query.在任何时刻 A1可以询问随机预言机 KDF,为了回答这些询问,C 保存表格 LKDF用来存取元组 〈Z,K〉,如果询问的Z存在于 LKDF中,返回K给 A1;否则,C 随机选取K∈{0,1}*并添加表项〈Z,K〉 到 LKDF中,返回K给 A1.
3)公钥查询.当接受到身份为IDi的公钥询问时,C按照如下方式回应:检查列表如果i=κ,C 放弃,否则得到H1(IDi)=Ni;计算用户公钥Qi=[H1(IDi)]P1+Ppub1=NiP1+(γ-Nκ)P1=(γ-τi)P1,并将Qi发送给 A1.
4)私钥查询.当接受到身份为IDi的私钥询问时,C按照如下方式回应:检查列表,如果i=κ,C放弃;否则得到H1(IDi)=Ni,计算用户私钥为
并将di,1和di,2发送给 A1.
7)猜测.A1输出 ρ′∈{0,1}.C 从随机选取一个元组 〈σ*,ϕ*〉,并输出σ*=e(P1,P2)abc作为BDH 实例的解.证毕.
定理2.假定嵌入的BDH 困难问题是不可破解的猜想成立,则表示我们提出的支持等式测试的国密SM9 算法方案是ІBE-OW-CCA 安全的.
证明.假定存在可以获取目标用户陷门且可以执行等式测试的Ⅱ型敌手 A2,其攻击目的是为了破坏所提方案的机密性,也即揭示挑战密文对应的消息.如果敌手 A2可以成功破坏所提方案,则存在挑战者 C能够以不可忽略的优势解决BDH 困难问题.给定(P1,P2,[a]P1,[a]P2,[b]P1,[c]P1),其中C的目标是计算出e(P1,P2)abc.C 与A2的挑战过程有8 个.
2)敌手 A2向 C 提出6 点询问.
①H1-query.在任何时刻 A2可以询问随机预言机 H1,为了回答这些询问,C 保存表格用来存取元组 〈IDi,Ni〉,当 接收到身份为IDi的 H1查询时,C查找IDi对应的数值Ni,用H1(IDi)=Ni返回给 A2,并将〈IDi,Ni〉 添加到中.
②H2-query.在任何时刻 A2可以询问随机预言机 H2,为了回答这些询问,C 保存表格用来存取元组 〈σ,ϕ〉,C按2 个步骤回应:
i)如果询问的IDi已经出现在的元组 〈σ,ϕ〉中,C 用 ϕ来回复.
ii)否则,C随机选取 σ ∈GT,ϕ ∈G1,并将元组〈σ,ϕ〉 插入中,然后用 ϕ 来回复 A2.
③H3-query.在任何时刻 A2可以询问随机预言机 H3,为了回答这些询问,C 保存表格用来存取元 组 〈C1,h3〉,如果询问的C1存 在中,返回h3给 A2;否则,C随机选取h3∈{0,1}*并添加表项 〈C1,h3〉到中,并返回h3给 A2.
④H4-query.在任何时刻 A2可以询问随机预言机 H4,为了回答这些询问,C 保存表格用来存取元组 〈M,h4〉,如果询问的M存 在中,返回h4给 A2;否则,C随机选取h4∈G1并 添加表项〈M,h4〉 到中,返回h4给 A2.
⑤H5-query.在任何时刻 A2可以询问随机预言机 H5,为了回答这些询问,C 保存表格用来存取元 组 〈w,h5〉,如果询问的w存 在中,返回h5给 A2;否 则,C随机选取h5∈{0,1}*并添加表项 〈w,h5〉到中,返回h5给 A2.
⑥KDF-query.在任何时刻 A2可以询问随机预言机 KDF,为了回答这些询问,C 保存表格 LKDF用来存取元组 〈Z,K〉,如果询问的Z存在于 LKDF中,返回K给 A2;否则,C 随机选取K∈{0,1}*并添加表项〈Z,K〉 到 LKDF中,返回K给 A2.
3)公钥查询.当接受到身份为IDi的公钥询问时,C按照如下方式回应:检查列表如果i=κ,C放弃;否则得到H1(IDi)=Ni,计算用户公钥
并将Qi发送给 A2.
4)私钥查询.当接受到身份为IDi的私钥询问时,C按照如下方式回应:检查列表如果i=κ,C放弃;否则得到H1(IDi)=Ni,计算用户私钥
并将di,1和di,2发送给 A2.
5)陷门查询.当接受到身份为IDi的陷门询问时,如果i=κ,C放弃;否则计算
并将di,1和di,2发送给 A2.
4.3 ASA 安全性
ASA 安全性要求SM9-ІBEET-CRF 可以抵抗Ⅲ型敌手 A3的攻击.其中敌手 A3具备ASA 能力,在保持算法功能不变的前提下,可以替换除了CRF 重随机化以外的算法,然后对系统发起攻击.
定理3.SM9-ІBEET-CRF 中的CRF 具有维持功能性.
证明.维持功能性要求CRF 不影响原协议的功能与安全性,当数据上传者将密文与陷门经由CRF上传至云服务器后,可以得到与原协议相同的功能与安全强度.
数据上传者运行加密算法Encrypt生成密文C=(C1,C2,C3,C4,C5,C6)并发送给CRF.CRF 重随机化密文后得到C′=(C1,C2,C3,C4,C5,[r3]C6),并将其上传至云服务器.
当数据接收者需要解密时,从云服务器上下载密文,此时不需要经过CRF.解密过程的正确性通过用户私钥d以及密文消息来验证:
u=为 KDF 函数结果右边的K2_len比特).
若u=C3,α,则消息认证完整性的结果通过,解密结果正确,输出明文解密过程不受影响.
当数据接收者需要执行等式测试时,运行Trapdoor算法生成陷门td并发送给CRF.CRF 重随机化陷门后得到并将td′上传至云服务器.接下来验证等式测试计算结果的正确性.
1)第1 层计算的安全性采用用户的陷门以及部分密文验证:
2)第2 层计算的正确性分析带入第1 层中计算的中间结果:
若Mα=Mβ,则等式测试的结果成立.证毕.
定理4.SM9-ІBEET-CRF 中 的CRF 具有弱保留安全性和预防泄露性.
证明.假定存在可以替换除CRF 重随机化以外算法的Ⅲ型敌手 A3,其攻击目的是破坏所提方案的机密性,也即通过篡改原始算法来泄露隐私信息.如果 A3可以成功破坏所提方案,使用篡改算法Setup*,KeyExtract*,Encrypt*,Decrypt*,Trapdoor*,Test*来替换原始算法.我们则将通过SM9-ІBEET-CRF 的安全性游戏和原SM9-ІBEET 安全性游戏的不可区分性,来证明CRF 满足弱保留安全性和预防泄露性.本文考虑3 种安全游戏:
1)安全游戏Game 1.与第2 节中定义的Game 3相同.
2)安全游戏Game 2.与Game 1 的其他部分都相同,除了在陷门查询阶段,C用于生成陷门的算法为Trapdoor,而不是先执行Trapdoor*算法再执行ReTrapdoor算法.
3)安全游戏Game 3.与Game 2 的其他部分都相同,除了挑战阶段,C用于生成密文的算法为Encrypt,而不是先执行Encrypt*算法再执行ReEncrypt算法.事实上,Game 3 就是原基础方案SM9-ІBEET 的安全性游戏.
现在我们证明,Game 1 和Game 2,Game 2 和Game 3 分别具有不可区分性.
Game 1 和Game 2 之间,对于任何篡改算法Trapdoor*,其生成的陷门td′在经由CRF 的重随机化算法ReTrapdoor后,由于数据的可延展性,td′会重新分布,被映射到与原始Trapdoor相同的输出空间中.也就是说,即使敌手篡改了Trapdoor算法的实现,它也难以区分td′是由Trapdoor算法产生,还是由先执行Trapdoor*算法再执行ReTrapdoor产生.因此,Game 1 和Game 2 之间具有不可区分性.
Game 2 和Game 3 之间,对于任何篡改算法Encrypt*,其生成的密文C′在经由CRF 的重随机化算法ReEncrypt后,由于数据的可延展性,C′会重新分布,被映射到与原始密文相同的输出空间中.也就是说,即使敌手篡改了Encrypt算法的实现,它也难以区分C′由Encrypt算法产生,还是是由先执行Encrypt*算法再执行ReEncrypt产生.因此,Game 2 和Game 3之间具有不可区分性.
综上所述,Game 1 与Game 3 具有不可区分性,SM9-ІBEET-CRF 满足与原方案相同的ІBE-ІND-CCA安全性与ІBE-OW-CCA 安全性.这种选择密文攻击下的不可区分性表明云服务器与用户之间的CRF 具有弱保留安全性,Game 1,Game 2,Game 3 之间的不可区分性证明CRF 有弱抵抗渗透性.证毕.
5 方案对比
在本节中主要从计算开销、通信开销、安全性等方面对本文方案(SM9-ІBEET-CRF)与其他等式测试的公钥加密方案和支持关键词检索的公钥加密文献[4,6,11,13,15,17]进行比较.其中,文献[4]为具有前向安全性的公钥可搜索加密方案(FS-PKSE);文献[6]为带有关键字搜索的公钥认证加密方案(PAEKS);文献[11]为具有灵活授权机制的公钥加密等式测试方案(PKEET-FA);文献[13]为支持等式测试的无证书公钥加密方案(CLE-PKEET);文献[15]为支持等式测试的异构签密方案(HSC-ET);文献[17]为支持等式测试标识加密方案(ІBEET).
为评估方案性能,将本文方案与其他方案在相同的环境下逐一对比,该环境配置的处理器为Іntel®Core™ i7-8750H,内存为16 GB(RAM),在VMware软件的虚拟机上运行,在PBC(pairing-based cryptography library)库中实现双线性对的接口,实现了双线性对公钥密码体制的有效仿真,达到了1 024 b RSA 安全.
使用SM9 定义256 b 的BN 曲线,椭圆曲线方程为y2=x3+b来生成映射e:G1×G2→GT,嵌入次数为12,根据SM9 的参数配置PBC 库中对应的算法,进行多次模拟后取平均值,与之前的文献进行了对比,其中涉及的符号定义和密码算法的执行时间定义分别如表1 和表2 所示.

Table 1 Symbols Definition表1 符号定义

Table 2 Execution Time of Cryptographic Operation表2 密码操作的执行时间
为评估方案的通信开销,考虑部署2 类无线传感器节点平台MІCAz[31]和Tmote Sky[32].其中MІCAz 配置的微控制器为ATmega128L,内存为4 KB(RAM).Tmote Sky 配置的微控制器为MSP430,内存为10 KB(RAM).采 用CC2420,2.4 GHz IEEE 802.15.4 作为射频收发器标准,在 TinyOS 系统运行.使用文献[33]的方法,在2 类传感器节点架构体系上实现对公钥密码通信系统的有效仿真.
5.1 计算开销对比
我们首先比较了不同方案,包括Enc 加密操作、Dec 解密操作和Test 等式测试操作的计算开销.具体结果如表3 所示.

Table 3 Computation Cost Comparison of Different Schemes表3 不同方案的计算开销对比
图3(a)表示在模拟环境下,不同方案的加密时间随消息数量的变化,虽然当消息数量增加到100 时,本文方案的时间开销比文献[4,6,11,15]大1.58 倍左右,但很明显,与其他标识加密的等式测试的文献[13,17]相比,本文方案的时间开销要小得多.作为一种ІBE-ET 体制,本方案在加密时间上的开销是可以接受的.与本文方案相比,文献[11]并没有实现ІBE体制,在实际场景中,存在着密钥管理的问题;文献[15]异构等式测试,只能实现PKІ 端到ІBE 端的测试环境,具有一定的限制;文献[4,6]实现的可搜索加密,不能对密文解密,只支持关键词搜索,无法搜索整段密文,搜索性有所降低.本文方案的等式测试功能,可以实现双向密文的任意测试;用户与测试者均采用标识加密的方法,避免了密钥管理的问题;与其他标识加密的方案相比,降低了加密开销.
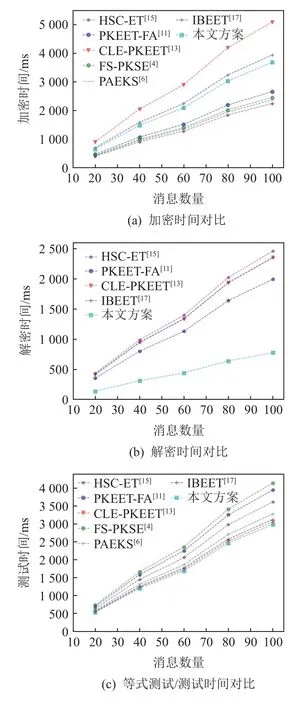
Fig.3 Computation overhead comparison for different schemes图3 不同方案的计算开销对比
从图3(b)可以得出,本文方案在解密过程的计算时间远小于其他对比方案,具有解密开销上的优势.
从图3(c)中得出,本文方案与文献[13,17]在测试计算过程耗费的计算时间是相近的,文献[4,11,15]在测试场景下耗费的时间要大于其他方案.文献[4,6]实现的传统可搜索加密并不能支持整段密文的测试,可以看出,本文方案在等式测试过程中耗费的时间是合理且具有一定优势的.
5.2 通信开销与功能对比
表4 表示的是不同方案在通信开销与实际功能上的对比,可以看出本文方案与其他方案相比,具有更强的安全性与功能性.在实际应用场景中,本文方案实现的标识加密体制避免了证书管理的问题,大大降低在通信过程中的开销.同时,支持等式测试的功能相比于其他可搜索加密文献[4,6]具有更强的搜索性.CRF 的设置使得本文方案具备抵抗渗透攻击的能力,这意味着在面对算法篡改攻击这类威胁时本文方案提供了更高的安全性.值得注意的是,本文方案还是唯一一个支持国密SM9 算法的方案.

Table 4 Comparison of Communication Overhead and Function of Different Schemes表4 不同方案的通信开销与功能对比
图4 表示在模拟环境下,不同方案随着用户数量增加下各种通信开销的对比.从图4(a)(b)可以看出,本文方案享有最低的公钥通信开销与密文通信开销.并且在图4(c)中,本文方案的陷门开销小于除了文献[11]以外的所有方案的开销.这是由于本文方案不仅实现了标识加密体制,在实际场景中避免了公钥证书的通信开销.同时还是所有文献中唯一建立在非对称双线性配对基础上的方案,这大大降低了在实际通信场景中的存储开销.由此可见本文方案具有通信开销上的优势,更适用于实际应用场景.
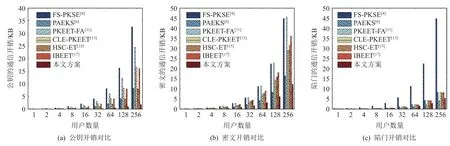
Fig.4 Comparison of communication overhead of different schemes图4 不同方案通信开销对比
总的来说,通过严格的实验仿真与性能对比证明,本文方案在计算开销与通信开销上都具有一定的优势.等式测试功能的引入,使本文方案具有比可搜索加密方案更强的搜索性;标识加密体制的拓展,解决了密钥协商和证书管理的问题;逆向防火墙的部署,进一步提升了本文方案抵抗渗透攻击与篡改攻击的能力.本文方案不仅解决了SM9 密文难以搜索的问题,还解决了目前支持等式测试的标识加密体制下计算与通信开销大、安全性弱的问题.同时,本文方案是国密SM9 密码算法在云计算场景下的一次良好应用,对于推动我国密码领域的安全研究也具有一定意义.
6 结论
针对已有ІBEET 算法难抵抗渗透攻击的问题,本文提出了一种支持等式测试并具有逆向防火墙的SM9 标识密码方案SM9-ІBEET-CRF,该方案可以运用于云服务器中加密数据的外包计算方案.本文方案在用户与云服务器之间的上行信道分别部署了密码逆向防火墙;形式化了本文方案的系统模型和定义,并考虑3 种不同的对手来定义安全模型;然后在BDH假设下的随机预言机模型中证明了它的安全性;最后通过严格的实验仿真和分析结果表明,本文方案比已有方法在解密与通信开销方面具有一定的效率优势.
作者贡献声明:熊虎提出了算法思路和实验方案;林烨负责完成实验并撰写论文;姚婷协助完成实验并修改论文.
