申威26010 众核处理器上Winograd 卷积算法的研究与优化

武 铮 金 旭 安 虹

（中国科学技术大学计算机科学与技术学院 合肥 230026）

（zhengwu@mail.ustc.edu.cn）

随着深度学习的快速发展，卷积神经网络（convolutional neural networks,CNNs）作为其最成熟的网络模型之一，被广泛应用于计算机视觉[1]、语音识别[2]、自动驾驶[3]、智能医疗健康[4]等领域，以获取更高的产业效率和更好的用户体验.而当前CNNs 高准确率的背后是巨大的计算代价，随着数据集变大、网络参数变多以及模型结构变得更加的复杂，CNNs 对运行效率的要求越来越高.对于整个CNNs 来说，90%以上的计算量都集中在卷积层中[5]，这也使得众核处理器上高性能并行卷积算法的研究成为了当前学术界和工业界的热门话题之一.

当前最受欢迎的卷积算法有4 种[6]，分别是直接卷积算法、GEMM 卷积算法、FFT 卷积算法和Winograd卷积算法.直接卷积算法是基于7 层循环做卷积，虽然实现简单，但是因为数据局部性差而导致性能不高.GEMM 卷积算法的核心是高效的矩阵乘实现，因为许多硬件平台上有可以直接使用的高效矩阵乘库，所以GEMM 卷积算法成为了加速卷积计算算法中非常受欢迎的算法，该算法可以分为显式的GEMM 卷积算法[7]和隐式的GEMM 卷积算法[8].相比于直接卷积算法，GEMM 卷积算法并不会改变整体的计算量，只是将离散的计算操作集中并连续执行，从而提高数据的局部性以实现卷积的高效执行.而FFT 卷积算法[9]和Winograd 卷积算法[10]则不同，两者都是通过将输入数据和卷积核数据线性变换，然后进行对应位相乘，中间结果再进行逆线性变换得到最终的输出数据.通过这种“变换—运算—逆变换”的过程，大大降低了卷积的计算复杂度.FFT 卷积算法将直接卷积算法的计算复杂度从O(OH2×FH2)降到了O(OH2×logOH)[6]，Winograd 卷积算法则进一步将卷积的计算复杂度降到了O((OH+FH-1)2)[10].

Winograd 卷积算法因其较低的计算复杂度，受到了广泛的关注与研究.Park 等人[11]针对卷积中大量的零权重和Winograd 变换中额外的加运算限制，提出了ZeroSkip 硬件机制和AddOpt 数据重用优化，增强后的算法能够取得51.8%的性能提升.Jia 等人[12]在Іntel Xeon Phi 上进行了任意卷积核维度的Wingorad卷积算法的优化与实现，对比最优的GPU 实现，在2D CNNs 上取得了旗鼓相当的性能，在3D CNNs 上性能更佳.武铮等人[13]利用Іntel KNL 的MCDRAM、多Memory/SNC 模式等微架构特性优化Winograd 卷积算法实现.测试VGG16，对比MKL-DNN 有2 倍多的性能加速.Mazaheri 等人[14]提出了一种基于符号计算的Winograd 卷积算法，利用元编程和自动调谐引入了能够为GPU 自动生成高效可移植Wingorad 卷积实现的系统.Jia 等人[15]提出了一种基于MegaKernel的Winograd 卷积实现，通过映射算法将不同的计算任务分配给GPU 线程块，并构建1 个按照依赖关系来获取和执行任务的调度器.结果表明，与cuDNN 的2 种Winograd 卷积实现相比，基于MegaKernel 的Winograd 卷积实现有1.25 倍和1.7 倍的性能加速.Castro 等人[16]通过汇编代码实现性能热点部分的方法，提出了一种优化的Wingorad 卷积算法OpenCNN，相比于cuDNN 的Winograd 卷积实现，在Turing RTX 2080Ti 和Ampere RTX 3090 上分别加速了1.76 倍和1.85 倍.王庆林等人[17]在融合数据scatter 和矩阵乘数据打包的基础上，针对飞腾多核处理器设计了一种不依赖矩阵乘库函数的Winograd 卷积实现，使得Mxnet 中VGG16 的前向计算获得了3.01～6.79 倍的性能加速.总的来说，近些年Winograd 卷积算法在通用处理器Іntel Xeon/Xeon Phi 和NVІDІA GPU 上得到了快速发展.与此同时，许多其他硬件平台的Winograd卷积加速也在不断吸引着研究人员投身其中，如国产多核处理器[17]、ARM CPU[18]、FPGA[19]等.

申威26010 众核处理器作为世界一流超算系统“神威·太湖之光”的核心算力来源，其低功耗高性能的特性使得其在人工智能领域拥有巨大潜力，8×8的从核阵列、软件控制的存储器层次结构、硬件支持的寄存器通信、从核的双流水指令运行等独特的架构特征既给了研究人员充足的可控空间，又提出了巨大的技术挑战.然而，该处理器上有关卷积算法的研究一直处于初级阶段，仅有的一些研究工作[5,8,20]也只是针对GEMM 卷积算法在该处理器上的高效并行实现.

综上所述，为了进一步探索申威26010 处理器上卷积算法的潜力，本文详细讨论了单精度Winograd 卷积算法在该处理器上的高性能并行设计，主要贡献有3 点：

1）提出了一种并行卷积算法—融合Winograd卷积算法，并为该算法设计了匹配的定制矩阵乘，使得该算法避免了传统Winograd 卷积算法对官方GEMM库接口的依赖.

2）提出的融合Winograd 卷积算法具有可视的执行过程，能够结合申威处理器典型架构特征进行更细粒度的计算访存优化.同时，通过设计合并的Winograd 变换模式、DMA 双缓冲、片上存储的强化使用、输出数据块的弹性处理以及指令重排等优化方案，在提升算法性能的同时，也为未来处理器上的并行研究工作提供了有意义的参考借鉴.

3）从优化效果、卷积性能和卷积神经网络性能3 个方面进行了实验.实验结果表明，在VGG 网络模型的测试中，融合Winograd 卷积算法性能高达传统Winograd 卷积算法性能的7.8 倍.通过对典型CNNs中常见卷积的收集测试，融合Winograd 卷积算法最高可以发挥申威处理器峰值性能的116.21%，平均可以达到93.14%.同时，通过测试对比定制矩阵乘和该处理器的通用GEMM，表明定制矩阵乘更有利于融合Winograd 卷积算法性能的发挥.

1 相关背景

1.1 Winograd 卷积算法

CNNs 主要包括卷积层、下采样层和全连接层等，其中卷积层和下采样层进行特征提取，全连接层在提取的最终特征上进行识别.综合来看，卷积层是CNNs 的关键动力，也是整个网络执行过程中最耗时的部分.考虑到卷积层的本质是卷积运算，因而，如何高效地设计卷积算法已经成为了一个热门研究话题.本文选择计算复杂度最低的Winograd 卷积算法作为研究对象，主要研究工作为该算法在国产申威26010 众核处理器上的高效并行.

对于通常的卷积运算，可以将输入数据标记为in[B][IC][IH][IW]，表示B个IC通道的样本，每个通道可以看作一个大小为IH×IW的输入特征映射；将卷积核数据标记为f tl[OC][IC][FH][FW]，表示OC组卷积核，每组IC个卷积核中每个卷积核的高度和宽度分别为FH和FW；将输出数据标记为out[B][OC][OH][OW]，表示B个OC通道的样本中每个通道可以看作一个大小为OH×OW的输出特征映射.除此之外，不同的填充大小和不同的跨步大小相互组合形成了不同的卷积形式，可以把高和宽的填充大小分别标记为padH和padW，类似地，高和宽的跨步大小则为stdH和stdW.卷积的执行过程为IC个输入特征映射和IC个卷积核一一对应卷积，然后累加IC个局部卷积结果，从而得到一个输出特征映射，因此一个完整的卷积需要OC×IC个卷积核.上述卷积过程可以简化为式（1）中关于in,flt,out的张量乘法和累加.

其中 0 ≤b＜B,0 ≤oc＜OC,0 ≤oh＜OH,0 ≤ow＜OW.

Winograd 卷积起源于有限脉冲响应（finite impulse response,FІR）滤波的最小滤波算法[10]，该最小滤波算法由r拍的FІR 滤波器生成m个输出，也就是F(m,r).此时，算法运算需要 µ(F(m,r))=m+r-1次乘法操作.对于1 维的Winograd 最小滤波算法可以表示为矩阵的形式：

通过嵌套1 维的Winograd 最小滤波算法可以得到2 维的Wingorad 最小滤波算法F(m×m,r×r)：

其中x表示输入，w表示过滤器，y表示输出；AT,G,BT表示该算法的系数矩阵；⊙表示矩阵的对应位相乘，即Hadamard 乘积.如果把x替换为卷积中的输入数据in，w替换为卷积中的卷积核数据flt，y替换为卷积中的输出数据out，参考文献[10]则可以得到Winograd 卷积算法，如算法1 所示.

算法1.Winograd 卷积算法.

对于Wingorad 卷积算法，系数矩阵AT,G,BT是由m和r决定的，以F(2×2,3×3)为例，此时有

1.2 申威26010 众核处理器

申威26010 众核处理器[21-22]是由上海高性能集成电路设计中心自主研发的一款国产异构众核处理器，支持64 b 自主神威指令级系统，采用分布式共享存储和片上计算阵列.如图1 所示，该处理器单芯片由4 个等价的核组（core group,CG）构成，核组间通过片上网络（network on chip,NoC）互连.每个核组由1个主核（management processing element,MPE）和64 个从核（computing processing element,CPE）组成，共计260 个计算核心.每个核组私有1 个4 路128 b 的DDR3主存控制器（memory controller,MC）和1 个协议处理单元（protocol processing unit,PPU），并通过MC 直连1 块8 GB 的DDR3 主存.

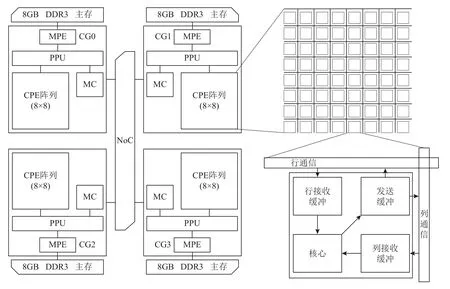
Fig.1 The architecture of ShenWei-26010 processor图1 申威26010 的处理器架构

主核和从核的工作频率都是1.45 GHz，两者都支持256 b 的浮点向量乘加指令，不同的是主核有2 条浮点运算流水，从核仅有1 条浮点运算流水.同时，双精度数据运算和单精度数据运算共用双精度浮点运算单元的微体系结构特征，使得该处理器上浮点数据的向量长度都为4.基于此，单核组从核阵列的理论单精度浮点峰值是742.4 GFLOPS，主核是23.2 GFLOPS.其中计算性能约97%来源于从核阵列，可见在该处理器上进行性能优化最为关键的任务就是如何高效地组织利用从核阵列的各种资源，以充分发挥从核阵列的计算性能.每个主核拥有2 级私有缓存，包括1 个32 KB 的L1 指令缓存、1 个32 KB 的L1数据缓存以及1 个256 KB 的L2 缓存.每个从核都有1 个16 KB 的L1 指令缓存和1 个64 KB 本地设备内存（local device memory,LDM）.从核阵列上的64 个从核共享一个大小为64 KB 的直接映射的L2 指令缓存.

该处理器为了尽可能缓解片外访存的压力，提供了2 个核心技术.一个是不同的主从核间的数据访问方式：1）gld/gst 离散访主存，即是从核直接对主存进行读写操作，这种方式的好处是简单易用，缺陷就是速度很慢，访存延迟高达278 个时钟周期；2）DMA（direct memory access）批量式访主存，即是从核先通过DMA 操作将主存数据提取到LDM，然后再对LDM 内的数据进行相关操作，整个过程的访存延迟较低，大约29 个时钟周期.其中，DMA 支持多种访存模式，应用最为广泛的有PE_MODE,ROW_MODE,BROW_MODE.另一个是寄存器通信实现同一核组内64 个从核的片上数据共享，为了有效支持这一机制，每个从核上配备了发送缓冲区、行接收缓冲区和列接收缓冲区，发送缓冲区可以缓冲6 个寄存器消息，2 个接收缓冲区可以分别缓冲4 个寄存器消息.寄存器通信机制需要注意3 点：1）通信时数据的大小固定为256 b；2）行和列都不同的2 个从核之间不能直接进行通信，需要借助同行或者同列上的从核作为中间转折点；3）通信的过程是匿名的，当多个从核发送消息到某个从核时，该从核基于先到先得的策略接收消息.Benchmarking[23]显示每个从核阵列上寄存器通信的带宽在P2P 模式和广播模式下分别可以达到637.25 GBps 和1 115.25 GBps.

申威26010 处理器每个从核支持2 条硬件流水线P0 和P1.其中，P0 支持浮点和整数的标量/向量操作，P1 支持数据迁移、比较、跳转和整数标量操作.2条流水线共享1 个指令解码器（instruction decoder,ІD）和1 个指令队列，每个时钟周期ІD 对队列中前2 条指令进行检测，当满足3 种情况时2 条指令可以同时被加载到2 条流水中：1）2 条指令同已发射未完成的指令不存在冲突；2）2 条指令间不存在写后读和写后写冲突；3）2 条指令可以分别被2 条流水处理.不难看出，如何混合交差程序中2 种类型的指令，使P0和P1 能够并行运行，对于该处理器性能的发挥起着重要的作用.

2 Winograd 卷积算法的并行优化

首先介绍提出的并行Winograd 卷积算法的整体设计思路.然后以F(2×2,3×3)为例，结合申威26010处理器架构特征，详细阐述该算法的各种计算和访存的优化方案.最后，对研究工作的通用性进行了分析，以期望能够对其他众核处理器上卷积研究提供有益的参考借鉴.

2.1 融合Winograd 卷积算法

如算法1 所示，Winograd 卷积算法的基本运算流程可以分为4 个部分：

现代处理器存在的普遍问题就是访存速度无法跟上计算能力，申威26010 处理器在这方面尤为严重，其每字节浮点计算率高达33.84[23].而通用处理器Іntel KNL 7290 和NVІDІA Tesla V100 分别为7.05[24]和7.78[25]，可见申威26010 处理器每字节的片外主存数据访问需要匹配远高于通用处理器的计算量.对于许多工作来说，要想充分发挥该处理器的性能，访存受限无疑是一个巨大的挑战.在上述Winograd 卷积算法的基本运算流程中，scatter 和gather 过程中的维度变化都是大量的离散访存操作，这将造成难以忍受的高额访存开销.为了解决上述问题，设置了新的数据格式—in[IH][IW][IC][B],flt[FH][FW][IC][OC],out[OH][OW][OC][B].这些数据格式的核心便是通过直接使用卷积过程中天然的矩阵乘关系（对应矩阵乘参数M,N,K分别为OC,B,IC），在避 免scatter 和gather 过程中的维度变化造成的高额访存开销的同时，也省去了存储中间数据而需要的额外内存资源.另一方面，将矩阵乘关系放到低维度中可以尽可能地提高整个算法执行过程中访存的连续性.

如图2（a）所示，Winograd 卷积最直接的实现方法就是在步骤3 中调用官方GEMM 库接口，而步骤1、步骤2 和步骤4 利用从核阵列并行执行Winograd 变换和Winograd 逆变换，这是一种传统的Winograd 卷积算法.该算法的优点是实现简单方便，缺点是中间数据需要消耗大量片外存储资源，极低的数据重用导致频繁的片外访存，高额的访存开销导致即便有着高性能的GEMM 库接口也难以实现卷积的高效运行.

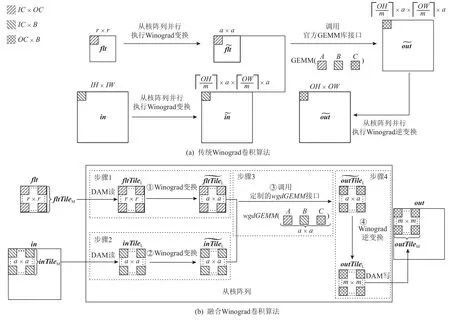
Fig.2 Basic framework of the fused Winograd convolution algorithm图2 融合Wingorad 卷积算法的基本框架

为了充分挖掘Winograd 卷积算法在申威26010处理器上的潜力，本文提出了一种不依赖官方GEMM库接口的算法.该算法能够将原本独立执行的Winograd变换、核心运算和Winograd 逆变换融合到一起，以充分发挥Winograd 卷积算法本身潜在的数据重用，从而尽可能降低访存对算法执行效率的影响，将其称之为“融合Winograd 卷积算法”.如图2（b）所示，将原卷积数据中的最后2 维看成1 个元素，那么in,flt,out则分别可以看成IH×IW,FH×FW,OH×OW的2维数组，且三者的单元素大小分别为IC×B,IC×OC,OC×B.在融合Winograd 算法中，步骤1 是通过DMA读取主存上r×r的卷积核数据块fltTileM到LDM 空间中的fltTileL，再通过Winograd 变换得到 α×α的步骤2 与步骤1 类似，先是读取 α×α的输入数据块inTileM到LDM 空间中的inTileL，然后通过Winograd 变换得到 α×α 的为了能够更好地适应融合Winograd 卷积算法中核心运算的实际情况，定制了高效的矩阵乘实现，并提供了便于该算法调用的从核函数接口wgdGEMM.步骤3 则是通过一一对应的方式调用 α×α 次的wgdGEMM，从而得到α×α的步骤4 执行Winograd 逆变换得到outTileL，并DMA 写回到主存中的对应位置outTileM.考虑整个过程中fltTileM是固定的，而inTileM和outTileM则是通过移动滑窗获取的，所以fltTileM将会被反复使用次.为了最大化fltTileM的时间局部性，设计算法仅且只执行1 次步骤1，并将变换后的结果长期驻留在片上存储LDM 中，直到卷积结束.步骤2、步骤3和步骤4则会随着滑窗的移动获取不同的inTileM和outTileM，继而执行次得到最终的输出数据out.

2.2 算法优化方案

后续内容将以F(2×2,3×3)为例进行详细阐述，即m=2,r=3,α=4.在2.1 节融合Winograd 卷积算法的基础上，结合申威26010 处理器的架构特征以及卷积运算的实际情况，进一步探索细粒度的访存和计算的优化方案.

2.2.1 合并的Winograd 变换模式

考虑到申威26010 处理器在进行矩阵乘的计算kernel 设计时，需要进行向量加载和寄存器通信.而该处理器仅支持双精度数据情况下单条指令完成向量加载和寄存器通信.如果是单精度数据的话，则需要分2 条指令进行，且这2 条指令之间存在写后读关系，将极大地降低计算kernel 的指令级并行度.因此，选择在片上存储LDM 中提前进行单精度数据和双精度数据的类型转换，从而保证送入wgdGEMM中的源数据都是双精度数据，以最大化卷积算法的指令级并行度.为此，可以设置融合Winograd 卷积算法中inTileL,fltTileL,outTileL用于存储LDM 上的单精度数据，则用于存储LDM 上的双精度数据.此时，对于输入数据块和卷积核数据块的Winograd 变换，以及输出数据块的Winograd 逆变换可以表示为：

在F(2×2,3×3) 中，BT,G,AT为确定的常数矩阵，具体值可以参见1.1 节.此时，i nTileL的维度为4 ×4×IC×B，可以将其简单视为 16×IC×B.相应的，维度也可以表示为 16×IC×B.那么对于输入数据块的Winograd 变换直观上可以分为二次矩阵乘运算，称之为“分离的Winograd 变换模式”，如图3 所示.其中i=0,1,…,IC×B-1，整个过程需要 224×IC×B次浮点运算.这种Winograd 变换方式虽然简单直观，但是不仅浮点运算量大，而且中间数据tmp会增大片上存储资源LDM 的开销，如果引入向量化则更会使这种额外的LDM 开销成倍增加.

Fig.3 Separated Winograd-transformed mode图3 分离的Winograd 变换模式

为了解决上述问题，设计了合并的Winograd 变换模式，通过将BTinTileLB的二次矩阵乘运算合并到一次，直接获取中每个元素关于inTileL中16个元素的线性关系，结果如图4 所示.

Fig.4 Merged Winograd-transformed mode图4 合并的Winograd 变换模式

通过合并的Winograd 变换模式，将浮点运算次数降低到了 48×IC×B，仅为原计算量的21.4%.同时，消除了中间数据带来的额外LDM 开销，使得向量化的使用不再受限制.因为申威26010 处理器的浮点向量长度为4，如果在合并的Winograd 变换模式中加入向量化，计算量将进一步降低至原计算量的5.35%.

类似地，对于fltTileL和通过合并的Winograd 变换模式，整个变换过程中计算量降为原计算量的11.43%；对于outTileL和通过合并的Winograd 变换模式，整个变换过程中计算量降为原计算量的9.52%.

2.2.2 DMA 双缓冲

申威26010 处理器支持异步的DMA 访存，因此有可能通过精心设计算法，从而尽可能地将DMA 访存开销分摊到核心运算上，缓解该处理器的片外访存压力，提高并行算法性能.

算法2.基于DMA 双缓冲的融合Winograd 卷积算法.

如算法2 所示，DMA 双缓冲的核心思想是通过预先执行1 次循环的DMA 操作，以消耗部分双倍的LDM 片上存储为代价，使得相邻2 次循环间的DMA操作和核心运算能够无依赖并行，从而掩藏掉部分访存时间.其中，ldst表示存储DMA 操作所需数据的LDM 空间，cmpt表示存储当前核心运算所需数据的LDM 空间.其中fltTileL用于DMA 读取卷积核数据块，并将fltTileL在Winograd 变换后的数据以双精度的形式放入考虑到Winograd 卷积中卷积核数据的反复使用，中数据将会常驻LDM 空间，直至卷积结束.同时，设置i nTileL[cmpt]和inTileL[ldst]用于双缓冲输入数据块inTileM的DMA 读取，设置outTileL[cmpt]和outTileL[ldst]用于双缓冲输出数据块outTileM的DMA 写回.相应地，分配和用于存储当前核心运算所需要的对应双精度数据.在算法2 中，实现了下一次inTileM的DMA读取和上一次outTileM的DMA 写回同当前核心运算的并行执行，理论最优情况下将会实现大约2 倍的性能提升.

2.2.3 片上存储的强化使用

申威26010 处理器提供了用户可控的片上存储LDM，但是单个从核的LDM 仅有64 KB，有限的LDM容量要求研究人员不得不精心设计算法，以尽可能提高片上存储资源的使用效率.在算法2 中，双缓冲虽然能够很好地实现核心运算和DMA 访存的并行，但是也会使部分使用中的LDM 空间翻倍，同时考虑到存储双精度数据带来的额外LDM 消耗，这些都给本就有限的LDM 带来了巨大压力.为了缓解算法2中片上存储的使用压力，设计了2 种优化方案：展开的LDM 强化使用和交错的LDM 强化使用.两者都是从算法设计的角度，通过重新组织算法的执行流程，寻找能够节省的LDM 空间.

假设B=IC=OC，如图5 所示，算法2 中初始使用的LDM 空间大小为580B2字节.在展开的LDM 强化使用中，将核心运算的整体展开并拆分成16 次独立的wgdGEMM，依次标识为wgdGEMM[0]～[15].同时，结合2.2.1 节中合并的Winograd 变换模式下的线性关系，如式（5）所示.

Fig.5 Unfolding LDM enhanced usage图5 展开的LDM 强化使用

Fig.6 Іnterleaving LDM enhanced usage图6 交错的LDM 强化使用

2.2.4 输出数据块的弹性处理

在融合Winograd 算法的优化中，都是以单个输出数据块为计算粒度设计算法，对于片上存储LDM的使用由B,IC,OC决定.但是并非任何情况下LDM都能够得到充分使用，当B,IC,OC三者较小时，会出现大量LDM 空间闲置的情况.针对上述问题，设计了输出数据块的弹性处理方案：通过增大算法基于输出数据块的计算粒度，使闲置的LDM 空间能够被使用起来，从而进一步探索融合Winograd 算法中潜在的数据局部性.

在进行Winograd 卷积时，移动输入数据的滑窗获取输入数据块时，2 个相邻的输入数据块之间会产生r-1的重叠.因此，对于以单个输出数据块为计算粒度的融合Winograd 算法，输入数据会出现反复被读取的情况.如图7 所示的卷积中，对于优化前的算法，输入数据将会被平均反复读取2.56 次.通过引入输出数据块的弹性处理，假设算法的计算粒度由单个输出数据块变为2 个输出数据块，那么每次只需要读取 4×6的inTileM相当于之前读取2 次 4×4的inTileM.因此，优化后的算法中输入数据的平均反复读取降为了1.92 次，相应地，输入数据的访存开销降低了25%.在不考虑LDM容量的情况下，可以设置单次计算输出数据块的数量为，此时将完全消除输入数据的不必要访存，使其访存局部性达到最大.

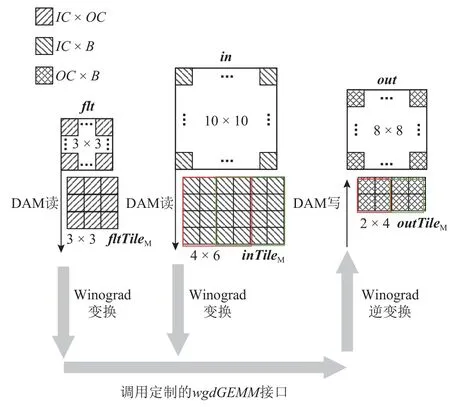
Fig.7 Processing two output data blocks in a single run图7 单次处理2 个输出数据块

2.2.5 定制的矩阵乘

融合Winograd 卷积算法相比传统Winograd 卷积算法的一大优势就在于其不依赖于GEMM 库接口，这使得整个Winograd 卷积的执行过程不再是透明的，从而让更细粒度的计算访存优化成为可能.为此，参考申威26010 处理器上的通用GEMM[26]，定制了匹配该算法的矩阵乘实现.为了方便后续说明，将算法中的卷积参数映射到对应的矩阵乘参数.其中，矩阵A,B,C分别对应每次DMA 访存的fltTileM,inTileM,outTileM数据块，矩阵乘参数M,N,K分别对应卷积中的OC,B,IC.

如图8 所示，整个定制矩阵乘实现可以分为2 部分：一部分为原始矩阵数据到单核组的任务映射；一部分为融合Winograd 卷积算法执行过程中调用的wgdGEMM.首先，前者由Winograd 变换、Winograd逆变换和核组级分块构成，对于Winograd 变换和Winograd 逆变换过程，在2.1 节中已经进行了详细的介绍，而核组级分块直接采用文献[26]中的分块原理，详细过程可以参考文献[26]中的研究工作.其次，需要注意Winograd 转换和Winograd 逆变换的线程级并行同wgdGEMM的线程级并行间是相对应的.以fltTileM为例，其在wgdGEMM中的对应矩阵A在进行线程级任务划分时，是通过对Kcg×Mcg矩阵块进行 8×8网格划分从而实现单个从核的任务映射.同理，fltTileM也将通过对 3×3个ICcg×OCcg（ICcg=Kcg,OCcg=Mcg）数据块的 8×8网格划分以实现卷积核的Winograd 变换过程的线程级并行.类似地，inTileM需要通对 4×4个ICcg×Bcg（ICcg=Kcg,Bcg=Ncg）数据块的 8×8网格划分以实现输入的Winograd 变换过程的线程级并行，outTileM需要通过对 2×2个OCcg×Bcg（OCcg=Mcg,Bcg=Ncg）数据块的 8×8网格划分以实现输出的Winograd 逆变换过程的线程级并行.最后，将结合融合Winograd 卷积算法中矩阵乘与文献[26]的2 点关键不同之处对wgdGEMM的实现进行详细介绍：1）不同一.矩阵乘不再是非转置的矩阵乘，而是矩阵A转置的矩阵乘；2）不同二.M,N,K通常情况下小于1 000[27].

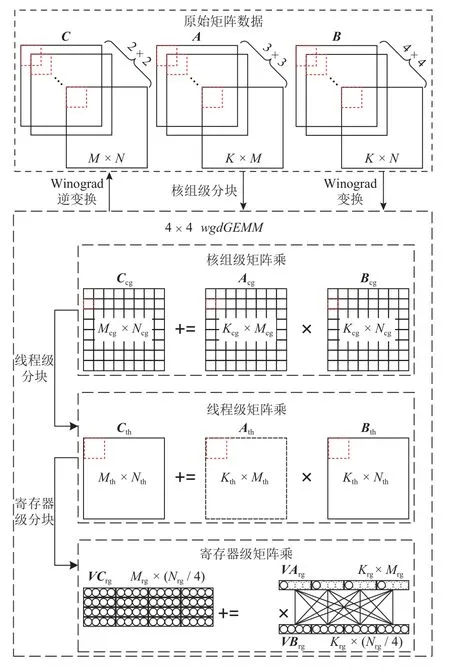
Fig.8 Customized matrix multiplication implementation图8 定制的矩阵乘实现

将16 个wgdGEMM绑定到一起作为融合Winograd卷积算法的单位计算粒度.其中，单个wgdGEMM可以分为3 个层次，分别为核组级矩阵乘、线程级矩阵乘和寄存器级矩阵乘.对于核组级矩阵乘，Acg,Bcg,Ccg分别对应算法中存储双精度数据的LDM 缓冲区当LDM 空间足够的情况下，Mcg,Ncg,Kcg分别与M,N,K相等.然后，基于单个核组上的 8×8从核阵列，对Acg,Bcg,Ccg进行 8×8网格形式的线程级分块，从而将单核组的矩阵乘映射到单线程的矩阵乘.为了满足Cth的计算需求，需要通过广播-广播的寄存器通信方案[26]，分别对Ath和Bth进行广播.在对从核进行Ath,Bth,Cth数据分配时，考虑到“不同一”，定制矩阵乘不再采用单一的行对行映射，而是按照行对行映射的方式为每个从核分配Bth和Cth，按照行对列映射的方式为每个从核分配Ath.由此，可得第i行第j列的从核将分配到Acg[j][i],Bcg[i][j],Ccg[i][j].通过这种混合映射方法，使得在广播-广播的寄存器通信中，分别对Ath进行行广播，对Bth进行列广播，从而使得每个从核上寄存器通信缓冲区资源能够得到充分利用.为了能够尽可能发挥wgdGEMM的指令级并行效率，通过寄存器级分块进一步将线程级矩阵乘划分为更细粒度的寄存器级矩阵乘，从而方便最底层核心指令序列的手动重排.考虑到“不同一”中可以先对Ath进行转置，将其维度从Kth×Mth变为Mth×Kth，再直接运用文献[26]中的方法.但是我们更希望能够避免这一转置带来的额外访存开销，为此，基于申威26010 处理器单精度向量长度为4 这一特性，设计了如图8 所示的寄存器级矩阵乘映射方案：1）通过vldd 指令依次装入Cth中元素，每次4 个元素，得到一个VCrg[Mrg][Nrg/4]的向量数组；2）通过ldder 指令依次装入Ath的单个元素进行向量扩展，得到一个VArg[Krg][Mrg]的向量数组，并行广播；3）通过vldc 指令依次装入Bth中元素，每次4 个元素，得到一个VBrg[Krg][Nrg/4]的向量数组，并列广播；4）通过vmad 指令对VArg和VBrg的所有向量数据进行全相连的乘法运算，并同VCrg中对应向量元素进行累加运算5）通过vstd 指令将计算结果写入Cth的对应位置.其中，每执行一次方案1和方案5，相应的方案2～4将会被执行次，不难看出方案2～4 组成了寄存器级矩阵乘的核心指令序列.为了保证寄存器级矩阵乘的运算效率，取Krg=1使得累加运算过程不存在数据依赖.同时，考虑到申威26010 处理器除去零寄存器和栈指针（stack pointer，SP）寄存器能够自由使用的向量寄存器数为30，所以有

再考虑整个线程级矩阵乘的计算访存比，所以有

在保证涉及到的每个向量元素能够匹配1 个独立向量寄存器的情况下，为了最大化计算访存比，减少不必要的访存开销，结合式（6）（7），可得因此，对于寄存器级矩阵乘，分配4 个向量寄存器存储VArg、4 个向量寄存器存储VBrg和16 个向量寄存器存储VCrg.

申威26010 处理器每个从核支持2 条不同的流水线P0 和P1，其中P0 支持浮点和整数的标量/向量操作，而P1 支持数据迁移、比较、跳转和整数标量操作.为了能够获得高性能的wgdGEMM，可以通过手写汇编保证寄存器级矩阵乘核心指令序列尽可能精简，同时手动重排指令序列以充分发挥从核的双流水指令运行机制.通过对上述寄存器级矩阵乘的描述，可以得到理想情况下向量寄存器的分配.其中，4个向量寄存器用于载入VArg数据，标记为AR0～AR3；4 个向量寄存器用于载入VBrg数据，标记为BR0～BR3；16 个向量寄存器用于存储VCrg数据，标记为CR00～CR33.由此，可以得出寄存器级矩阵乘最内层循环核心指令序列如图9（a）左侧所示，执行时间为25 个时钟周期，此时整个执行过程几乎处于单流水状态.为了能够真正启动从核的双流水模式，对初始指令序列手动重排，重排后如图9（a）右侧所示.在最内层循环开始前，首先预取第1 次计算所需的AR0,AR1,BR0,BR1，然后在最内层循环指令序列中实现当前循环的计算前部分和访存后部分的双流水，以及当前循环的计算后部分和下一轮循环的访存前部分的双流水，最终优化后的指令序列的执行时间为16 个时钟周期，性能提升约56.25%.此时，虽然从核双流水的性能得以充分发挥，但是Mrg=4且Nrg=16，却要求矩阵乘中M是32 的倍数且N是128 的倍数.虽然当M和N不满足此要求时可以使用填充的方式先满足倍数要求再进行运算，但是考虑到“不同二”，这种开销往往是不可忽视的.例如，当M=64,N=64,K=128时，依照图9（a）中实现，需要额外1 倍的计算和访存，这些不必要的计算和访存将极大地降低算法的性能.

Fig.9 Іnstruction reordering图9 指令重排

为了尽可能缓解这一问题，依照Mrg=4且Nrg=16 时指令重排的思想，对Mrg∈{1,2,3,4}和Nrg∈{4,8,12,16}组成的16 种情况中余下的15 种情况的实现分别进行了指令重排，如图9（b）所示Mrg=4且Nrg=8时的情况.为了配合这一实现，将Mth分为2 部分[0,Mthmod(Mth,4)) 和[Mth-mod(Mth,4),Mth).类似地，Nth也 被分为 [0,Nth-mod(Nth,16)) 和 [Nth-mod(Nth,16),Nth).通过Mth的2 部分和Nth的2 部分的一一对应关系可以将寄存器级矩阵乘分为4 个部分.此时，对于M=64,N=64,K=128的情况则可以直接运算，不需要任何多余的计算和访存开销.

2.3 通用性分析

本文研究工作虽然是面向国产申威26010 处理器探索并行卷积算法的高性能实现，但是仍然对其他众核处理器硬件平台具有一定的借鉴意义.如2.1节中Winograd 变换、核心运算和Winograd 逆变换融合执行以尽可能减少分离执行造成的高额访存开销的思想，2.2.1 节中合并Winograd 变换过程并向量化以避免存储中间数据带来的额外片上存储资源的开销并降低变换过程中的计算量，以及2.2.4 节中弹性处理输出数据块的数量以充分利用片上存储资源，这些优化方案都是脱离硬件平台特征的，可以直接应用于其他众核处理器.除此之外，其他的优化方案，比如DMA 双缓冲、片上存储的强化使用、定制矩阵乘实现这些工作则是同申威26010 处理器架构特征紧密联系的，虽然无法直接应用于其他众核处理器平台，但是对于某些类似架构特征的硬件平台仍然可以提供一些参考价值.

如上所述，Winograd 融合卷积算法可以分为与架构无关的优化方案和与架构相关的优化方案2 个部分，对于新一代的申威26010Pro 处理器[28-29]，主要关注于架构相关的优化方案的适用性.而架构相关的优化方案主要是DMA 双缓冲、片上存储的强化使用、定制矩阵乘实现，其中申威26010Pro 处理器对于DMA 双缓冲是依旧支持的；片上存储LDM 则由原来的64 KB 增加到了256 KB，更多的片上存储资源更有利于降低主存的访问频率；定制矩阵乘的实现中，最大变化来自于寄存器通信机制的取消和SІMD 指令向量长度的增加，但是仍然具备对单核组从核间的数据通信的支持，也就是新的RMA（remote memory access），向量长度的增加则更有利于浮点性能的发挥.因此，综合上述分析不难看出，融合Winograd 卷积算法对于申威26010Pro 处理器同样适用.

3 实验结果与分析

申威26010 处理器的配置如表1 所示.

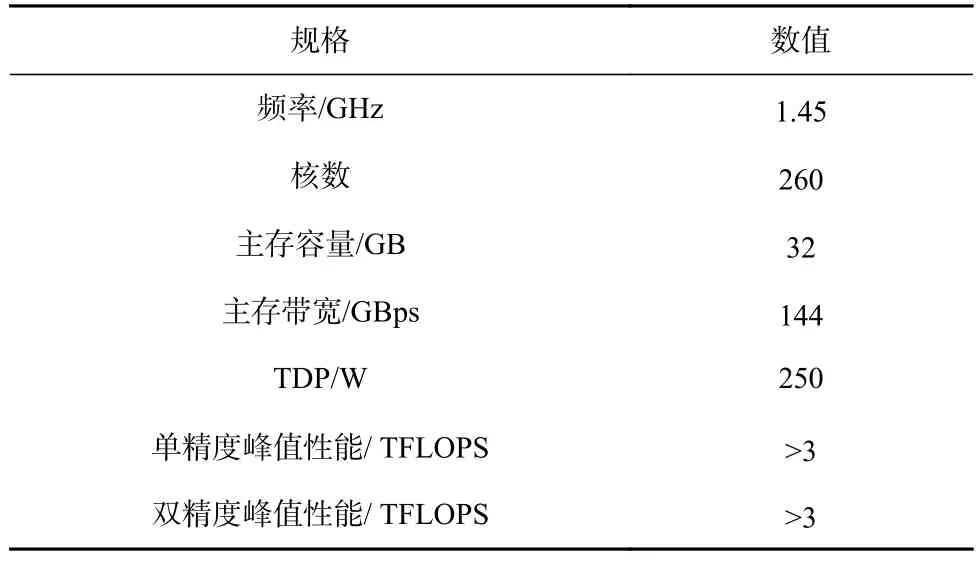
Table 1 Configure Parameters for ShenWei-26010 Processor表1 申威 26010 处理器配置参数

本次实验全部在申威26010 处理器单核组上进行，因为跨不同核组的并行通常由更高编程级别的用户自己处理[26,30].实验中将本文提出的不依赖官方GEMM 库接口的融合Winograd 卷积算法标记为fusedWgdConv，类似地，将依赖官方GEMM 库接口的传统Winograd 卷积算法作为基准测试对象，并标记为simpleWgdConv.从4 个不同的角度设计实验，从而充分展示研究工作的成果和价值.1）通过对不同优化方案的累加设计实验，测试各个优化方案的效果；2）抽取典型卷积神经网络模型AlexNet,GoogleNet,ResNet,VGG 中的常见卷积层，测试评估fusedWgdConv在实际应用场景中的性能；3）基于fusedWgdConv，在深度学习框架Caffe 中测试不同批大小下VGG 网络模型的卷积性能提升.4）对fusedWgdConv 调用的wgdGEMM的效果进行了测试.为了保证测试结果的精确性，所有测试均迭代10 次，去掉1 个最优值和1个最差值，取剩余8 个测试结果的平均值.

3.1 优化效果测试

选取VGG 中的卷积作为测试实例，并以simpleWgd-Conv 作为测试基准，测试并记录fusedWgdConv 在不同优化方案累加下相比于simpleWgdConv 的性能加速.

通过对不同优化方法的累加，可以得到7 个版本的fusedWgdConv，分别为：1）ІNІT，融合Winograd 变换、核心运算和Winograd 逆变换的执行过程，初步实现fusedWgdConv；2）MERGE，在ІNІT 版本的基础上引入合并的Winograd 变换模式；3）DB_ІN，在MERGE版本的基础上，双缓冲实现in的DMA 访存和核心运算的并行；4）DB_OUT，在DB_ІN 版本的基础上，双缓冲实现out的DMA 访存和核心运算的并行；5）LDM_OPT，在DB_OUT 的基础上，引入展开的LDM 强化使用和交错的LDM 强化使用，缓解有限片上存储资源的使用压力，降低算法的片外访存开销；6）MULTІ_OUT，在LDM_OPT 的基础上，考虑小规模卷积时LDM 大量闲置的情况，引入输出数据块的弹性处理机制，使得任何情况下算法都能充分利用片上存储资源；7）ADD_F43，通过添加F(4×4,3×3)的实现，探索不同输出数据块大小的影响.

如图10 所示，初步实现了fusedWgdConv 的ІNІT版本相比simpleWgdConv 有67%的性能提升，可见ІNІT 的基本设计思路能够明显降低simpleWgdConv依赖官方GEMM 库接口造成的高额访存开销.依据Winograd 变换系数能够提前确定这一特征，将原本分离的Winograd 变换模式替换为合并的Winograd变换模式，同时引入向量化，不仅消除了额外的LDM使用，而且大大降低了Winograd 变换过程中的计算量，基于此的MERGE 版本性能是simpleWgdConv 的2.9 倍.申威26010 处理器支持DMA 的异步执行，通过对fusedWgdConv 的精心设计实现了in和out的DMA访存同核心运算的并行运行，使得大部分的片外访存开销得以被计算掩藏.基于此的DB_ІN 版本相比MERGE 版本性能提升了52.76%.进一步优化后的DB_OUT 版本相比MERGE 版本性能提升了74.14%.最终双缓冲使得fusedWgdConv 运行性能达到了simpleWgdConv 的5.05 倍.有限的片上存储资源限制了fusedWgdConv 的性能提升，为了能够尽可能提升片上存储的使用效率，设计了展开的LDM 强化使用以减少数据类型变换带来的额外LDM 消耗，以及交错的LDM 强化使用降低inTileL双缓冲的LDM 需求，由此LDM_OPT 版本性能相比DB_OUT 版本进一步提升了48.51%.MULTІ_OUT 版本中的输出数据块弹性处理仅对小规模卷积有作用，因此对算法性能提升并不明显，其最终性能是simpleWgdConv 的7.75 倍.ADD_F43 版本相比于MULTІ_OUT 版本的性能提升非常微弱，主要原因在于fusedWgdConv 单核组每次至少要处理1 个输出数据块所涉及到的Winograd变换、Winograd 逆变换和核心运算，造成片上存储资源的开销很高.当算法由F(2×2,3×3)扩展到F(4×4,3×3)时，单个输出数据块的规模增加了4 倍，大大增加了对片上存储资源的需求，而申威26010处理器有限的片上存储资源不足以很好地支撑fused-WgdConv 的进一步扩展.

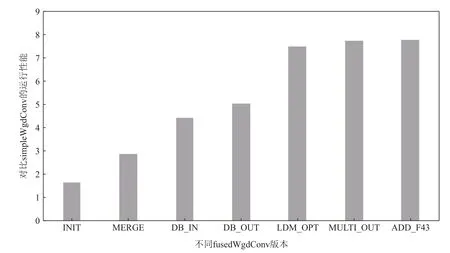
Fig.10 Performance comparison of different fusedWgdConv versions and simpleWgdConv图10 不同fusedWgdConv 版本和simpleWgdConv 的性能对比

综合来看，fusedWgdConv 相比simpleWgdConv 对于申威26010 处理器上的卷积有显著的性能提升.

3.2 卷积性能测试

为了能够进一步验证fusedWgdConv 对常用卷积是否具有现实意义，抽取典型卷积神经网络模型AlexNet，GoogleNet，RestNet,VGG 中卷积层的卷积参数，并测试对比fusedWgdConv 和simpleWgdConv 的卷积性能.一般来说，卷积性能测试时的测试标准是运行时的性能，但是为了能够更好地观察算法对硬件处理器的使用效果，实验选择运行时相对理论峰值性能的百分比作为测试标准，计算公式为硬件效率=.

如图11 所示，将抽取的卷积按照计算量由小到大排列，同时对2 种常见的卷积形式进行测试分析：1）填充为0 且跨步为1；2）填充为1 且跨步为1.从总体卷积测试来看，fusedWgdConv 在无填充和有填充的情况下平均硬件效率分别为95.08%和91.2%，分别是simpleWgdConv 下卷积性能的14.54 倍和14.52 倍.可以看出，fusedWgdConv 的卷积能够很好地适应现实中的卷积场景.从单个卷积测试来看，无填充时，fusedWgdConv 性能最小时是simpleWgdConv 性能的3.02 倍，最大时可以达到62.81 倍；有填充时，fusedWgd-Conv 相比simpleWgdConv，卷积性能与无填充时差不多，在3.01～62.72 倍不等.其中，无填充和有填充情况下，fusedWgdConv 的最高硬件效率可以分别达到116.21%和111.41%.可以看出，fusedWgdConv 能够很好地发挥申威26010 处理器的硬件性能，且相比simpleWgdConv有明显的性能提升.

Fig.11 Hardware efficiency of ShenWei-26010 processor for different convoltuions图11 不同卷积下申威26010 处理器的硬件效率

3.3 卷积神经网络性能测试

为了测试评估本文工作在实际使用中的效果，以原始版本的Caffe 为基准，基于fusedWgdConv 测试不同批大小下VGG 模型的卷积性能提升.同时，考虑到Caffe 中卷积的数据格式为N-C-H-W，fused-WgdConv 的数据格式为H-W-C-N，标记Caffe-FWC和Caffe-FWC-DFT 这 2 个版本的Caffe，分别表示基于fusedWgdConv 的Caffe 和基于fusedWgdConv 且进行数据格式转换的Caffe.

如图12 所示，Caffe-FWC 的性能加速比在3.4～9.8之间.而Caffe-FWC-DFT 虽然仍能带来可观的性能提升，但是数据格式转换大约占了整个卷积执行过程的40.5%，因此是不容忽视的.但是数据转换过程完全是可以避免的，只需要将卷积神经网络模型中的所有网络层格式设计成H-W-C-N即可.此时在实际使用中仅需对样本数据进行 1 次的N-C-H-W到H-W-C-N的数据格式转换即可，其代价相对于后续成千上万次的网络模型的循环迭代是非常微小的.这也是我们目前正在致力于的整个DNN 库的研究工作，具体内容会在以后的文章中进行详细阐述.

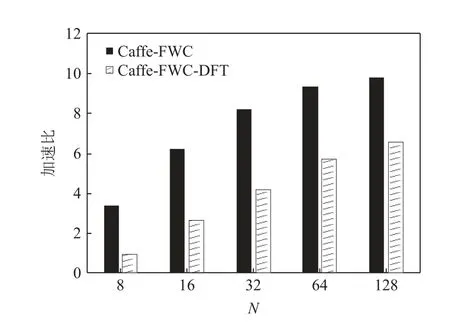
Fig.12 Performance speedup of Caffe with different versions图12 不同版本Caffe 的性能加速比

3.4 定制矩阵乘效果测试

fusedWgdConv 的关键点之一就是与其匹配的定制矩阵乘，如2.2.5 节所示，wgdGEMM在申威26010处理器现有的通用GEMM[26]的基础上，针对2 点不同进行了设计.针对“不同一”，设计了混合映射的广播-广播的寄存器通信以及避免转置开销的寄存器级矩阵乘.相应的，针对”不同二”，对Mrg∈{1,2,3,4}和Nrg∈{4,8,12,16}组成的16 种情况下寄存器级矩阵乘的核心指令序列都进行了手写汇编和指令重排，而文献[26]只考虑了Mrg=4且Nrg=16的情况.

实验选择8 组矩阵乘场景作为测试对象，其中每组矩阵乘满足2 点：一是矩阵A转置；二矩阵的维度不同时满足Mrg=4和Nrg=16.同时，选取申 威26010 处理器现有的GEMM[26]作为基准，对比测试wgdGEMM的效果.假设GEMM 同wgdGEMM一 样所需数据已存在于LDM 中，如表2 所示为两者的运行时间.其中，wgdGEMM相对GEMM 性能加速比为0.202 3～0.278 8 不等，平均性能加速比约为0.239 9.由此可见，针对fusedWgdConv 定制矩阵乘是有必要的，且wgdGEMM相比GEMM 有明显的性能提升.

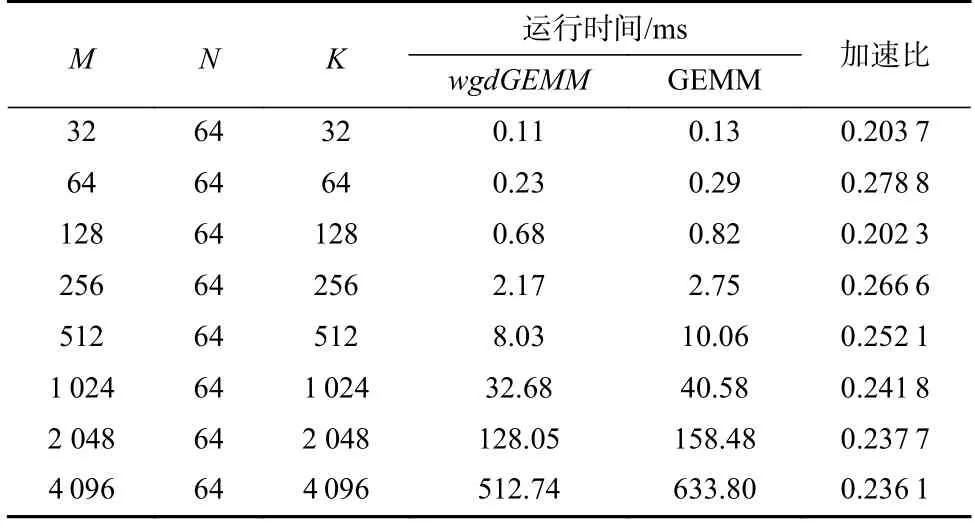
Table 2 Running Time for wgdGEMM and GEMM表2 wgdGEMM 和GEMM 的运行时间

4 总结展望

随着我国自主研发的申威26010 众核处理器在人工智能领域的快速发展，对该处理器上高性能卷积算法的实现也提出了更高的要求.而该处理器上卷积算法现有的研究尚处于初级阶段，本文针对这一问题，结合申威26010 处理器的架构特征，提出并实现了一种高性能并行的融合Winograd 卷积算法.该算法有2 个主要特点：1）不依赖于官方GEMM库接口，设计了匹配该算法的定制矩阵乘，并结合现实卷积计算特征和通用矩阵乘算法，在零开销情况下完成了矩阵转置，并对其寄存器级矩阵乘的核心指令序列进行了各种情况的指令重排；2）Winograd变换、核心运算和Winograd 逆变换过程的融合优化避免了三者分开执行时造成的反复读取主存数据带来的高额访存开销.此外，还设计了合并的Winograd变换模式加速Winograd 变换过程；DMA 双缓冲实现从核阵列上计算和访存的并行；展开和交错的LDM强化使用方法以提高有限片上存储资源的使用效率；输出数据块的弹性处理避免小规模卷积下片上存储资源的浪费，通过这些优化保证了融合Winograd 卷积算法在申威26010 处理器上的高性能并行.在实验分析中，以依赖官方GEMM 库接口的传统Winograd卷积算法为基准，从优化效果和卷积性能2 个方面进行测试分析，证明了融合Winograd 卷积算法不仅有远高于传统Winograd 卷积算法的性能，而且能够很好地应用于现实卷积场景.

未来将对本文工作进行扩展，结合其他网络层优化设计以及主流深度学习框架，进一步探索申威26010 众核处理器上深度学习的并行优化.

作者贡献声明：武铮提出算法思路，设计并实现具体的优化方案，撰写并修改论文；金旭参与算法实现、实验设计以及数据分析；安虹负责指导论文撰写.