意外充分性引导的深度神经网络测试样本生成
2024-04-29郭虹静陶传奇黄志球
郭虹静 陶传奇,2,3 黄志球,2
1(南京航空航天大学计算机科学与技术学院 南京 210016)
2(高安全系统的软件开发与验证技术工信部重点实验室(南京航空航天大学) 南京 210016)
3(计算机软件新技术国家重点实验室(南京大学) 南京 210023)
(guohongjing@nuaa.edu.cn)
以深度学习(deep learning,DL)为代表的人工智能技术迅猛发展,基于大量数据训练的深度神经网络(deep neural network,DNN)模型越来越多地被部署在智能软件系统中,并广泛应用在工业生产、社会生活、金融经济等各方面.然而,智能软件的可靠性、鲁棒性、安全性等问题也日益凸显,尤其在安全攸关领域,例如无人驾驶汽车系统、恶意软件检测系统以及飞机碰撞避免系统等,如不能有效加以防范,可能会导致重大损失甚至灾难性后果.例如,2018 年 3 月,Uber 公司在美国亚利桑那州开展汽车试验时发生了一起无人驾驶汽车将行人误识别为物体的意外事件,导致行人遭受了撞击[1].当前智能软件的核心组件是DNN 模型,通过DNN 模型的感知与决策实现智能功能.DNN 模型不遵循传统软件的编程范式,其决策逻辑是从训练集中学习而得[2-3],具有高度复杂的数据依赖性、内在行为不确定性等特点,样本中任何微小的扰动都可能导致模型做出难以理解的错误行为.因此,有效保证DNN 模型的质量至关重要.软件测试是发现软件错误、保障质量的关键手段.为保证DNN 模型的可靠性,使用足够的测试样本对模型的一般行为和边界条件下的行为进行充分的测试是必要的[4].
DNN 模型的决策逻辑无法通过控制流、数据流分析等程序分析方法进行解析,模型的输入具有维度高、特征复杂的特点,导致以最大化语句或分支覆盖为引导的传统软件测试数据生成技术不再适用于DNN 模型[5-6].因此针对DNN 模型设计有效的测试样本生成方法是近年来深度学习测试领域的研究热点.覆盖引导的模糊测试(coverage-guided fuzzing,CGF)在传统软件测试中表现出较强的错误揭示能力,能够在有限的测试数据上自动化产生大量的、具有高代码覆盖率的测试数据[6].CGF 方法也被广泛用于DNN 模型的测试样本生成,以DNN 模型的测试覆盖率为指导准则,在原始测试集的基础上,通过对种子样本进行变异,生成新的测试样本,揭露原始测试集无法暴露的错误,并且使得衍生测试集具有更高的覆盖率[6-8].
在DNN 模型测试覆盖度量指标方面,Kim 等人[9]从测试样本多样性的角度,提出意外充分性(surprise adequacy,SA)指标,该指标量化单个测试样本相对训练集的“意外性”.在此基础上设计意外覆盖(surprise coverage,SC)准则,度量测试的充分程度.意外充分性是针对单个测试样本的指标,用于量化测试样本与训练集在DNN 模型内部神经元输出方面的差异.意外充分性值越低,表明该测试样本与训练集的神经元输出较为相似;值越高,表明该测试样本与训练集的神经元输出值差异越大,更有可能揭示DNN 模型隐藏的错误[9-11].尽管已提出的意外充分性指标能够捕捉测试样本相较于训练集的意外程度,但由于指标在度量时需要将DNN 模型一层的全部神经元的输出作为特征,执行时间开销较大[12].计算效率极大依赖于模型的规模,特定网络层的神经元数量越多,执行时间开销越大.此外,已提出的意外充分性度量指标未考虑神经元与模型决策结果之间的因果关系,即忽略神经元输出值对模型决策结果的贡献程度[13-14].
当前CGF 方法主要采用神经元覆盖[7]、强神经元激活覆盖[15]等结构性测试覆盖准则作为引导,较少考虑单个样本的揭错能力,缺乏基于意外充分性的测试样本生成方法.此外,种子测试样本是影响DNN模型测试样本生成有效性的关键.然而已有测试样本生成方法多采用随机的方式筛选种子样本,忽略对种子样本揭错能力的考虑;同时,筛选种子样本时未充分覆盖原始测试集的全部类别,生成的测试样本多样性不足.因此,利用覆盖引导的模糊测试思想,将样本的意外充分性作为引导,在生成对抗样本的同时,能够最大化模型的意外覆盖率,即生成丰富多样的测试样本,进一步探索模型的输入空间,以提升测试充分性.
针对上述问题,本文提出了意外充分性引导的深度神经网络(surprise adequacy-guided deep neural network,DeepSA)测试样本生成方法.考虑到对于决策结果影响较大的重要神经元能够刻画模型的决策逻辑,DNN模型在相似的样本上的决策逻辑很大程度上具有一定的相似性,利用重要神经元的输出值作为特征,从而可以更精准地刻画样本间的差异程度.因此DeepSA首先筛选出对于决策结果影响较大的神经元,利用这些神经元的输出改进意外充分性指标,并进一步提升计算效率.其次,基于测试样本的意外充分性选取种子样本;为了使得生成的样本能够探索模型的不同内部逻辑,选取种子样本时覆盖原始测试样本的所有类别.最后,利用覆盖引导的模糊测试思想,将样本的意外充分性和模型预测的类别概率间差异作为联合优化目标,利用梯度上升算法迭代产生扰动,对种子样本进行变异,生成新的测试样本.
本文在5 组经典的深度学习数据集和模型上对DeepSA 开展了实验评估,实验对象涵盖4 个分类模型和1 个回归模型.实验结果表明,改进的意外充分性指标能够精准地捕捉异常的测试样本,并进一步提升计算效率.在测试样本生成方面,在最好情况下,LeNet4 模型与DeepGini[16]和RobOT[17]相比,基于DeepSA 种子选择策略生成的衍生测试集的意外覆盖率提升幅度分别为29.9%和95.4%.Fashion-LeNet5模型相比于DeepXplore[7]和DLFuzz[8],基于DeepSA种子选择策略生成的衍生测试集的意外覆盖率提升了33.7%和26.5%.
本文的主要贡献可总结为4 点:
1)提出了意外充分性引导的测试样本生成方法,基于意外充分性指标选取种子样本,并将样本的意外充分性作为反馈,迭代引导测试样本的生成.该方法能够在生成对抗样本的同时提升意外覆盖率.
2)改进了意外充分性指标,利用对于决策结果影响较大的神经元的输出值,量化模型在测试样本和训练样本上决策的差异;改进的指标可减少测试集意外充分性计算的时间开销.
3)在4 种公开图像数据集和5 个DNN 模型上验证了所提方法的有效性.在4 个分类模型上,相比于已有方法,DeepSA 生成的衍生测试集的意外覆盖率提升达到23.4%,7.5%,3.9%,33.7%.
4)基于Tensorflow1.10.0,Keras2.2.0 等框架 实现了DeepSA,方法实现源代码及DeepSA 生成的测试样本已共享至网址①https://github.com/TestingAІGroup/DeepSA,以方便其他研究者开展后续研究.
1 背景知识
1.1 覆盖引导的深度神经网络模糊测试
受传统测试覆盖思想的启发,已有研究学者提出了多种基于神经元输出值的结构性测试覆盖指标,以此定义测试数据对于 DNN 模型的覆盖率.例如,神经元覆盖[7]、K多段区域神经元覆盖[15]、强神经元激活覆盖[15]、激活路径覆盖[18]、t-路组合稠密覆盖[19]、状态覆盖[20]等.在此基础上,研究人员提出面向DNN模型的CGF 技术,通过执行待测DNN 模型,基于覆盖率和模型预测结果,指导模糊测试过程[21].
CGF 技术首先依据种子选择策略选取测试样本,然后依据变异策略对种子样本进行变异,生成新的测试数据,旨在揭露原始测试集无法暴露的错误,并且使得衍生测试集具有更高的测试覆盖率.变异策略直接影响CGF 方法的错误揭示能力,通常采用基于梯度的变异方法、基于神经网络的变异方法、基于搜索的变异方法等.基于梯度的变异方法将种子样本的变异建模为联合优化问题进行求解,即生成使得结构性覆盖最大化并且模型输出错误结果的样本,通过设计损失函数作为优化目标,在最大化目标的驱动下,采用梯度上升等算法迭代产生扰动,将扰动添加到种子样本中生成新的测试样本.
1.2 意外充分性与意外覆盖
Kim 等人[9]从非结构性角度引入了意外充分性的概率,提出了基于似然的意外充分性(likelihoodbased surprise adequacy,LSA)和基于距离的意外充分性(distance-based surprise adequacy,DSA),在此基础上度量测试集的意外覆盖率.本节主要介绍意外充分性度量指标及意外覆盖准则.
首先给出相关符号的定义,给定测试样本x,表示DNN模型第l层全部神经元的输出值构成的向量,为训练集T中所有样本的神经元输出值向量构成的集合;D(x)为模型预测的测试样本x的类别,TD(x)表示与该测试样本属于同一类别的训练样本子集.
1)基于似然的意外充分性.给定测试样本x,该指标利用核密度估计来估计DNN 模型D在训练过程中出现相似样本的可能性.其定义为:
其中K为高斯核函数,H为带宽.对于分类模型,可利用TD(x)替换公式中的T.LSA指标表明与训练集差异较大的测试样本的概率密度函数值较小.
2)基于距离的意外充分性.该指标基于单个测试样本的神经元输出向量与训练样本的神经元输出向量间的欧氏距离来量化样本间的差异.
其中xa表示与x距离最近且属于同类别的训练样本,xb表示与xa距离最近且属于不同类别的训练样本.DSA指标表明越接近2 个类间决策边界的测试样本与训练集的差异越大.由于DSA指标利用样本间的距离刻画DNN 模型类别间的决策边界,因此该指标仅适用于分类模型.
3)意外覆盖.给定一个测试集,L为测试集的SA值下界,U为预先设置的SA值上界,将[L,U]区间平均分成k段,Si表示第i段;若测试样本x计算出的DSA值或LSA值位于段Si内,则该段被覆盖.意外覆盖计算被测试集覆盖的段的比例为:
其中测试集对应的SC值越高,则表明该测试集更加多样化,既包含与训练数据相似的输入,又包含与训练数据具有差异的输入.DSC和LSC分别表示基于DSA指标和LSA指标度量的意外覆盖准则.
2 意外充分性引导的测试样本生成
2.1 方法框架
本文所提出的DeepSA 方法的框架如图1 所示,首先引入分层相关性传播(layer-wise relevance propagation,LRP)算法[22-23],识别对于DNN 模型决策结果贡献大的重要神经元,将这些神经元的输出值作为特征,改进意外充分性指标.然后基于测试样本的意外充分性选取种子样本;采用基于梯度的种子样本变异方法,利用梯度上升算法对目标损失函数求解产生扰动,生成中间样本;将中间样本的意外充分性作为反馈,指导后续测试样本的生成并不断迭代.在生成有效的对抗性测试样本的同时,最大化模型的意外覆盖率,以探索DNN 模型的输入空间.

Fig.1 Framework of DeepSA approach图1 DeepSA 方法框架
2.2 重要神经元筛选
DeepSA 选取网络中的特定隐藏层作为目标层,利用LRP 算法[22],输入训练集,利用神经元的正向输出值和神经元间的权重,度量DNN 模型中各神经元与输出结果的相关性得分,捕捉网络中每个神经元对决策的实际贡献,识别目标层中的重要神经元.
以图像分类算法为例,将一张图像输入至DNN模型中,LRP 算法利用深度泰勒分解技术,以神经网络中神经元间的权重为引导,结合神经元的正向输出值,将模型输出层的预测值逐层分解并反向传播到输入空间,为图像输入的每个像素分配与输出结果相关的贡献值,从而确定输入和输出之间的相关性.DeepSA 将训练样本x输入至DNN 模型中,获取输出的样本x所属类别对应的概率f(x),每层网络层中所有神经元的相关性得分之和等于f(x).针对每个训练样本,LRP 算法将模型的输出逐层反向传播,依据式(4)计算目标层中每个神经元的相关性得分.
针对目标层中的每个神经元,DeepSA 将其在每个训练样本上计算出的相关性得分进行累加,得到每个神经元在训练集上的相关性得分;选取每层相关性得分为前m%的神经元作为重要神经元,构成目标层重要神经元集合,表示为针对不同的DNN模型,可通过实验找到m的最优取值.
2.3 意外充分性引导的测试样本生成
DeepSA 基于CGF 的思想,将样本的意外充分性作为反馈,迭代引导测试样本的生成.
2.3.1 改进的意外充分性
意外充分性指标利用DNN 模型产生的中间表示,即样本的神经元输出值,量化单个测试样本与训练集的差异,能够发现使得模型产生错误预测行为的测试样本.DeepSA 将目标层中重要神经元的输出值作为特征,利用代替式(1)(2)中的Nl,以度量测试样本的LSA值和DSA值.DeepSA 改进的2 种意外充分性度量指标表示为LSAv和DSAv,对应的意外覆盖指标表示为LSCv和DSCv.
2.3.2 种子测试样本选择
CGF 方法需要从原始测试集中选取一定数量的样本作为种子样本,依据变异策略对其进行变异.种子样本是模糊测试的基础,对于测试的有效性具有关键影响[6].多样性的种子测试样本能够提升模糊测试探索DNN 模型内部的能力;并且对具有错误揭示能力的种子样本进行变异生成新的测试样本,能够尽可能多地揭露原始测试集无法暴露的错误.因此,DeepSA 结合种子样本的类别标签,基于测试样本的意外充分性LSAv值和DSAv值优先筛选具有揭错能力的种子测试样本作为后续测试样本迭代生成的基础.
DeepSA 设计2 种种子测试样本选择策略.第1种选择策略表示为ST-Dall 和ST-Lall,即分别依据DSAv值和LSAv值将测试样本进行降序排序,选取前num个样本作为种子测试样本,其中num为预先定义的种子测试样本数量.第2 种是考虑类别标签的选择策略ST-Dper 和ST-Lper.由于不同类别的种子测试样本能够探索模型的不同内部逻辑,受沐燕舟等人[24]的工作启发,DeepSA 在选择种子测试样本时,不仅考虑意外充分性,而且覆盖到原始测试集中包含的全部测试样本类别.需要说明的是,沐燕舟等人[24]提出的测试样本选择方法旨在筛选小规模的测试子集,以精确估计原始测试集的准确率.尽管该方法与DeepSA 在测试样本选择上的目标不同,但其核心思想与动机类似,即筛选测试样本时尽可能多地覆盖到原始测试集中包含的测试样本类别.具体而言,ST-Dper 和ST-Lper 种子样本选择策略以样本的真实标签作为区分测试样本类别的依据,针对每个类别,算法选取相同数量的样本作为种子样本,以保证所选的种子测试样本集覆盖全部的样本类别.种子测试样本选择算法如算法1 所示.
算法1.种子测试样本选择算法.
种子测试样本选择算法将被测DNN 模型D、训练集train_data、测试集test_data以及测试样本的类别标签集合labels作为输入;输出种子测试样本集针对每个类别,算法选取相同数量的样本作为种子样本,以保证所选的种子测试样本集覆盖全部的测试样本类别,num_label表示每个类别需要筛选出的种子样本数量.算法首先将测试集test_data输入至DNN模型中,比较样本的真实标签和模型预测结果,筛选被模型正确预测的测试样本子集,存储至test_corr中(行③);针对每种类别标签la,筛选属于该类别并被DNN 模型正确预测的测试样本,构成测试子集label_corr(行⑤).然后利用函数SA_var()计算测试样本子集中各样本的LSAv值或DSAv值,结果存储在意外充分性值列表sa_list中(行⑥~⑧).接着依据意外充分性值,通过函数sort()将类别标签为la的测试样本进行降序排序,选择前num_label个测试样本作为种子样本,存储在seeds_label中(行⑨).最后将各类别筛选出的种子样本存储在种子测试样本集seeds_list中(行⑩).
2.3.3 测试样本生成
DeepSA 采用基于梯度的变异方法[6,8],将如何对种子样本迭代产生扰动建模成联合优化问题,通过设计目标损失函数,将目标损失函数作为优化目标,采用梯度上升算法最大化目标损失函数,产生扰动,迭代生成测试样本.目标损失函数定义为:
其中给定样本x′,DNN 模型Softmax 层输出的概率分布向量为(P(c),P(c1),…,P(cm)),各分量为模型预测的样本属于各类别的概率.P(c)表示概率分布向量中最大的概率值,c为其对应的类别标签;ci(1≤i≤k)表示预测概率低于c的前i个类标签之一,k=4.目标损失函数的前半部分旨在使得生成的测试样本跨越DNN 模型类别间的决策边界[17],使模型产生错误分类.SAv(x′) 表示样本x′的意外充分性LSAv值或DSAv值,用于增大测试样本相对于训练集的重要神经元输出差异.算法2 展示了测试样本生成的伪代码.
算法2.意外充分性引导的测试样本生成算法.
算法2 将被测DNN 模型D、种子测试样本集合seeds_list、训练集train_data以及预先设置的学习速率lr作为输入;算法输出为生成的对抗样本adv_samples.算法使用s_list存储每个种子产生的中间样本,对于s_list中的每个样本,算法首先得到模型预测的类别标签c_orig、最大预测概率p以及低于p的前K个预测概率p_topk(行⑥);其次利用函数SA_var()度量该样本的意外充分性sa_orig、目标值obj以及目标对原始样本的梯度grads(行⑦~⑨).然后依据梯度构造中间样本x′(行⑪),其中函数random()用于产生随机值,防止持续迭代的过程中产生相同的微小扰动.将目标obj对原始样本的梯度grads乘以学习速率lr,再乘以随机值(random()+0.5),作为添加到原始样本上的微小扰动,以产生中间样本x′.之后算法获取模型预测的该中间样本的类别c_fup、意外充分性sa_fup以及与原始样本的距离dis(行⑫~⑭).依据意外充分性值是否能够提升以及样本间的距离约束来决定生成的中间样本是否应该被保留,用于下一轮迭代生成测试样本(行⑮~⑰).函数dis_constraint()用于计算样本间的范数距离,dis表示样本间的距离.判定中间样本与原始样本的预测类别,若不一致则该中间样本即为对抗性测试样本,添加到adv_samples中(行⑱~⑳).经过多轮迭代,生成更多的对抗性测试样本.由于生成的中间样本都需要度量其意外充分性值,DeepSA 方法筛选重要神经元,能够减少中间样本意外充分性度量的时间开销,以提升测试样本生成的效率.
算法设置种子测试样本的总数量num=100,迭代次数iters=5,学习速率lr=0.1,距离阈值 ε=0.5;设置目标函数权值 λ=1,λ值越大表明算法更倾向于生成能够提升意外充分性的样本.为方便描述算法2 的时间复杂度,使用sj表示种子测试样本集seeds_list中第j个种子样本对应的中间样本列表s_list中样本的数量,算法2 的时间复杂度表示为
3 实验设计
3.1 研究问题
1)问题1:DeepSA 方法是否能够有效地生成测试样本.
问题1 分别从生成的对抗样本数量和意外覆盖率提升2 个方面评估DeepSA 测试样本生成方法的有效性.由于DeepSA 结合DNN 模型输出的测试样本类别概率差异及改进的意外充分性设计目标优化函数,本文提出的测试样本生成方法仅适用于分类模型.针对问题1,本文仅在分类模型上开展实验分析.
实验将DeepSA 分别与DeepXplore[7]和DLFuzz[8]对比,分析在相同的迭代停止条件下,DeepSA 是否能够生成更多的对抗性测试样本,并提升测试集的意外覆盖率.DeepXplore 与DLFuzz 均采用基于梯度的变异方法.DeepXplore 旨在生成能够最大化不同DNN 模型输出结果之间的差异和神经元覆盖率的对抗性测试样本.DLFuzz 将最大化神经元覆盖和最大化模型预测错误的概率作为联合目标函数,生成对抗性测试样本.DeepXplore 和DLFuzz 随机选取样本作为种子样本,种子样本随机选择策略表示为random.
为了进一步分析DeepSA 提出的种子测试样本选择策略的有效性,问题1 利用不同的种子测试样本选择策略,选取相同数量的种子测试样本,对比分析不同种子样本策略在测试样本生成上的效果.DeepSA提出的模糊策略分别表示为DFuzz 和LFuzz,即分别利用DSAv和LSAv指标设计目标损失函数.对比实验基于DFuzz 和LFuzz 模糊策略,分别采用DeepGini[16]提出的基于模型预测概率的选择策略以及RobOT[17]提出的基于样本损失值的BE-ST(bi-end strategy)选择策略,从原始测试集中筛选种子测试样本.此外,问题1 进一步分析不同种子样本数量对测试样本生成的影响,种子测试样本数量分别取50 和100.
2)问题2:改进的意外充分性指标是否能够捕捉异常的测试样本.
为了探究以重要神经元输出值为特征改进的意外充分性指标是否能够更加精准地捕捉到异常的测试样本,问题2 依据LSAv值或DSAv值将测试样本降序排序,计算DNN 模型在具有不同样本数量的测试子集上的准确率或均方误差(mean squared error,MSE).问题2 在分类模型和回归模型上开展实验评估.针对分类模型,测试样本子集中包含的样本数量分别为100,300,500,1 000,2 000,4 000,6 000,8 000.分类模型在测试子集上的准确率越低,则表明可以捕捉到更多的异常样本.针对回归模型,基于改进的意外充分性度量值分别构建5 个测试样本子集,包含的样本数量分别为100,1 000,2 000,4 000,5 000.采用MSE 评估改进的意外充分性指标在回归模型上的效果;回归模型在测试子集上的MSE 值越高,表明利用该指标捕捉到的异常样本的数量越多.实验中,m的取值范围为10~100,步长设置为10;m=100 表示选取目标层的全部神经元,即原始意外充分性指标的特征选取方式.
3)问题3:改进的意外充分性度量指标的运行时间开销.
DeepSA 在度量样本的意外充分性时预先筛选出重要神经元,为了探究以重要神经元输出值为特征是否能够提升意外充分性计算的性能,问题3 对比基于不同m取值的测试集意外充分性计算的时间开销.从获取目标层神经元的输出开始计时,直至测试集中所有样本的意外充分性值度量完毕,不包含DNN模型加载以及测试集、训练集的读取.m取值的设置与问题2 中的一致.
3.2 实验对象和评测指标
3.2.1 实验对象
本文利用MNІST[25],CІFAR10[26],Fashion-MNІST[27],Udacity Self-driving Car Challenge[28]图像数据集,在4个分类模型和1 个回归模型上开展方法的有效性评估,表1 列出了待测模型及数据集的详细信息.采用的数据集被广泛应用在DNN 模型测试的研究中,MNІST 是手写数字0~9 的图像数据集;CІFAR10 数据集包含10 种类别的真实世界中的对象,如鸟类、飞机等的图像;Fashion-MNІST 数据集包含10 种类别商品,如裙子、T 恤等的图像;Udacity Self-driving Car Challenge 数据集包含从行驶的汽车挡风玻璃上捕获的摄像头图像,被广泛用于自动驾驶系统的方向盘转向角预测.表1 中第3 列和第4 列列出了分类模型在测试集上达到的准确率以及回归模型在测试集上的MSE 值.考虑到一些隐藏层中的神经元数量较少,提取出的神经元输出值向量无法精准区分样本间差异,Deep-SA 在选取目标层时,重点考虑了层数较深且包含一定数量神经元的卷积层、激活层或全连接层.

Table 1 DNN Models and Data Sets表1 DNN 模型和数据集
3.2.2 评估指标
1)对抗性测试样本数量.在相同的种子测试样本数量、迭代次数、学习速率、样本距离阈值的情况下,对比分析不同方法生成的对抗性测试样本数量.
2)意外覆盖率差值.将原始测试集与DeepSA 生成的测试样本合并为衍生测试集,本文采用原始测试集和衍生测试集在意外覆盖率上的差值来衡量DeepSA 生成的测试样本是否能够提升意外覆盖.表2展示了本文在度量原始测试集的意外覆盖率DSCv和LSCv时分别采用的意外充分性上界值和段的数量.
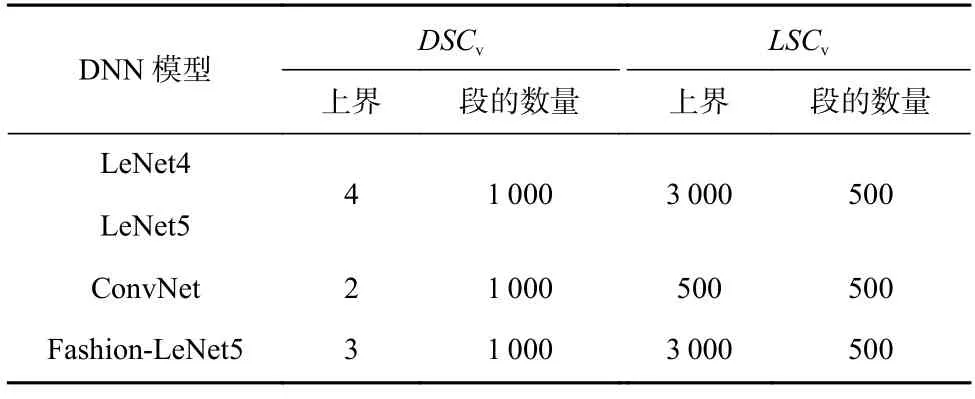
Table 2 Parameter Configurations of Surprise Coverage表2 意外覆盖率的参数配置
4 实验结果分析
4.1 测试样本生成的有效性
表3 展示了采用不同的模糊策略和种子样本选择策略生成的对抗样本数量、原始测试集的意外覆盖率以及衍生测试集对应的意外覆盖率差值.种子样本数量均设置为100.
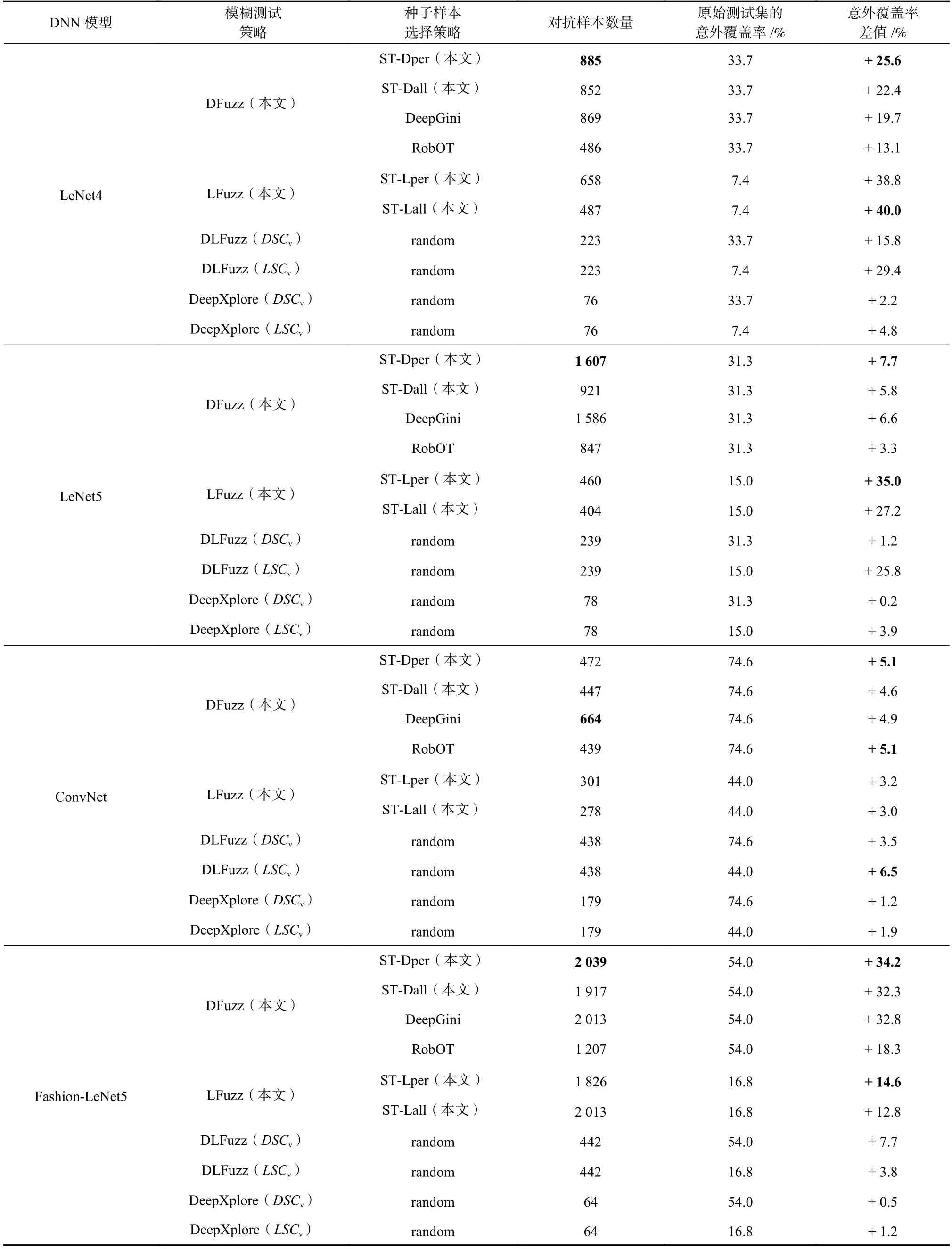
Table 3 The Number of Generated Adversarial Examples and Corresponding Surprise Coverage Differences表3 生成的对抗样本数量及对应的意外覆盖率差值
从生成的对抗样本数量上看,DeepSA 在LeNet4,LeNet5,Fashion-LeNet5 模型上生成的最多对抗样本数量分别为:885,1 607,2 039.在种子样本数量和迭代次数相同的条件下,利用ST-Dper 种子样本选择策略和DFuzz 模糊策略,生成的对抗样本数量较多.例如,在相同的模糊测试策略DFuzz 下,相比于RobOT 提出的BE-ST 种子选择策略,利用ST-Dper 策略生成的对抗样本数量提升幅度分别达到82.1%,89.7%,7.5%,68.9%.此外,利用ST-Dper 和ST-Lper 作为种子测试样本选择策略生成的对抗样本的数量多于采用STDall 及ST-Lall 策略生成的.
相较于已有的测试样本生成方法DeepXplore 和DLFuzz,在相同的种子样本数量、迭代次数、迭代停止条件下,DeepSA 在对抗样本生成数量上表现较为显著.具体而言,对于4 个分类模型,DeepSA 相比Deep-Xplore 能够多生成809,1 529,293,1 975 个对抗样本;与DLFuzz 相比,DeepSA 能够多生成662,1 368,34,1 597个对抗样本.
从意外覆盖率差值的角度,基于DeepSA 提出的模糊策略和种子样本选择策略生成的衍生测试样本,能够有效提升意外覆盖率.其中,在4 个DNN 模型上,DeepSA 的DSCv提升最大值分别为25.6%,7.7%,5.1%,34.2%.LSCv提升的最大值分别为40.0%,35.0%,6.5%,14.6%.在大多数情况下,采用ST-Dper 和ST-Lper 作为种子样本选择策略,衍生测试集提升的意外覆盖率更高.例如,在Fashion-LeNet5 模型上,尽管LFuzz+ST-Lper 策略生成的对抗样本数量少于LFuzz+STLall 策略生成的,但前者对应的意外覆盖率差值高于后者.在ConvNet 模型上,基于ST-Dper 种子选择策略生成的对抗样本数量略少于使用DeepGini 策略生成的对抗样本,但意外覆盖率提升幅度达4.1%.在LeNet4 模型上,采用ST-Dper 种子选择策略取得的意外覆盖率差值(25.6%)高于DeepGini 策略(19.7%)和RobOT 策略(13.1%).上述结果表明,在筛选种子测试样本时,覆盖原始测试集的所有类别能够生成更加多样化的样本,从而提升意外覆盖率,以进一步探索DNN 模型的输入空间.
与DeepXplore 和DLFuzz 相比,DeepSA 生成的衍生测试样本集的意外覆盖率提升显著.在4 个分类模型上,相比于DeepXplore,DeepSA 生成的衍生测试样本集的意外覆盖率DSCv显著提升,分别提升了23.4%,7.5%,3.9%,33.7%;LSCv意外覆盖率差值分别提升了35.2%,31.1%,1.3%,13.4%.与DLFuzz 相比,DeepSA 生成的衍生测试样本集的DSCv意外覆盖率差值分别提升了9.8%,6.5%,1.6%,26.5%;除ConvNet模型外,LSCv意外覆盖率差值分别提升了10.6%,9.2%,10.8%.
本文基于DFuzz 模糊策略和ST-Dper 种子样本选择策略,进一步分析不同种子样本数量对于测试样本生成的影响.表4 列出了种子样本数量分别为100 和50 时,DeepSA 生成的对抗样本数量及衍生测试集的意外覆盖率差值.结果表明,随着种子样本数量的增加,生成的对抗样本数量和意外覆盖率差值显著提升.此外,结合表3 可以观察到,与DeepXplore相比,DeepSA 使用仅50 个种子样本即可生成数量更多、意外覆盖率更高的衍生测试样本.在LeNet4,LeNet5,Fashion-LeNet5 模型上,DeepSA 基于50 个种子样本生成的对抗样本数量及衍生测试样本集意外覆盖率的提升均优于DLFuzz.
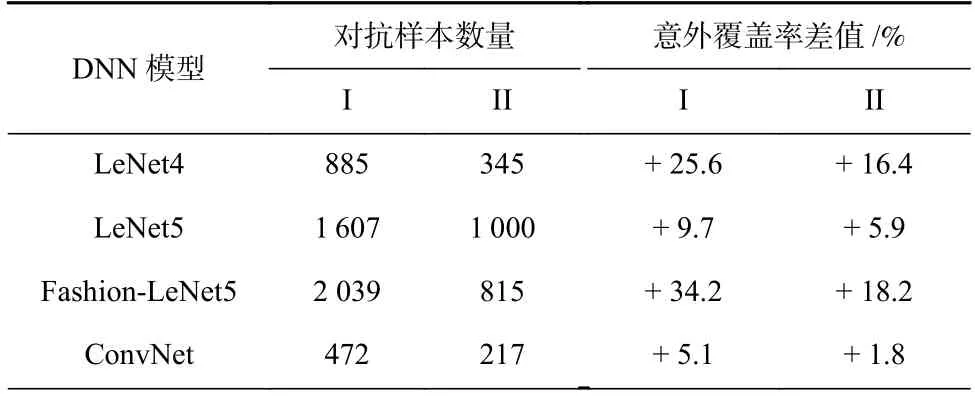
Table 4 Results of Test Samples Generated by DeepSA with Different Numbers of Seeds表4 不同种子样本数量下DeepSA 生成的测试样本结果
综上,DeepSA 能够有效地生成对抗性测试样本,生成的测试样本能够提升意外覆盖率.在选取种子样本时覆盖原始测试集中包含的所有测试样本类别,可以有效地提升衍生测试集的多样性.
4.2 改进的意外充分性的有效性
图2~5 分别展示了4 个待测分类模型在基于LSAv值和DSAv值排序的测试样本子集的准确率.DeepSA 通过对具有揭错能力的种子样本进行变异来迭代生成新的测试样本,种子样本数量设置为100,因此问题2 重点关注DNN 模型在LSAv值和DSAv值最高的前100 个测试样本的准确率.图2~5 分别展示了m=100 以及其余9 种m取值的最优前3 个配置的准确率结果.图2~5 中的实线表示模型在基于LSAv值排序的测试样本集上的准确率变化;虚线表示各模型在基于DSAv值排序的测试样本集上的准确率变化.
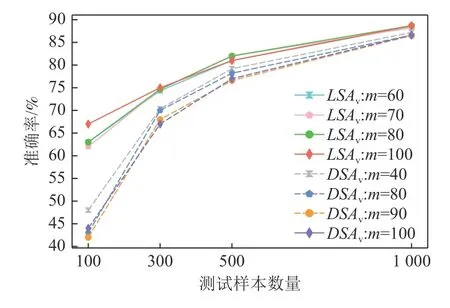
Fig.2 Accuracy of LeNet4 model on selected test subsets based on LSAv values and DSAv values图2 LeNet4 模型在基于LSAv 值和DSAv 值筛选的测试样本子集上的准确率

Fig.3 Accuracy of LeNet5 model on selected test subsets based on LSAv values and DSAv values图3 LeNet5 模型在基于LSAv 值和DSAv 值筛选的测试样本子集上的准确率
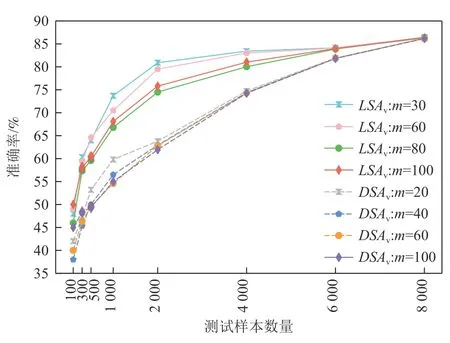
Fig.4 Accuracy of Fashion-LeNet5 model on selected test subsets based on LSAv values and DSAv values图4 Fashion-LeNet5 模型在基于LSAv 值和DSAv 值筛选的测试样本子集上的准确率
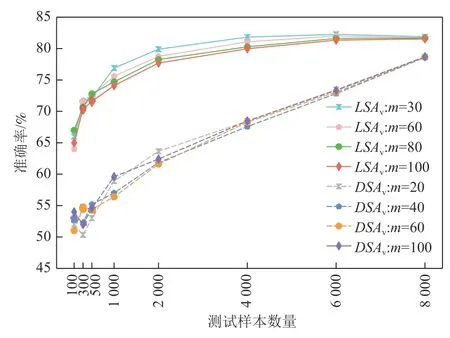
Fig.5 Accuracy of ConvNet model on selected test subsets based on LSAv values and DSAv values图5 ConvNet 模型在基于LSAv 值和DSAv 值筛选的测试样本子集上的准确率
从捕捉异常测试样本的角度,改进的意外充分性度量指标LSAv及DSAv能够有效提升原始指标的效果.通过分析图2~5 中呈现的准确率结果可以看出,LeNet4,LeNet5,Fashion-LeNet5,ConvNet 模型在LSAv值最高的前100 个测试样本上的最低准确率分别在m取值为70,80,80,80 时得到.与LSA指标相比,LSAv指标取得的准确率分别降低了5 个百分比,2 个百分比,4 个百分比,1 个百分比.例如,LeNet4 模型在LSA值最高的前100 个测试样本上的最高准确率为67%,在LSAv值最高的前100 个测试样本上的最低准确率为62%,准确率降低了5 个百分点.针对DSAv指标,LeNet4 和Fashion-LeNet5 模型在DSAv值最高的前100 个测试样本上的最低准确率分别在m取值为90 和40 时得到.例如,Fashion-LeNet5 模型在m=100 时的准确率为45%(模型DSAv值最高的前100 个样本上的最高准确率),而在m=40 时的准确率降低到38.0%,准确率降低的幅度达到15.6 个百分点.在LeNet5 和ConvNet 模型上,DSA指标的准确率分别为58 个百分点和54%,而在最佳m配置下,DSAv指标取得的准确率为55%和51%,相比DSA指标均降低了3 个百分点的准确率.
随着测试样本数量的增多,LSAv和DSAv指标与原始意外充分性指标的结果趋于接近.当测试样本数量为4 000,6 000,8 000 时,改进的意外充分性指标和原始指标在LeNet4 和LeNet5 模型上取得了一致的结果.随着意外充分性值较低的样本数量增多,模型的准确率有所提升.值得注意的是,LSAv指标在4个分 类模 型上更倾向于较大的m取值(m>60).当m>70 时,DSAv指标在LeNet4,LeNet5,ConvNet 模型上效果较好.后续还将进一步探索m取值的自动化配置方法.
表5 展示了待测回归模型Dave_orig 在基于LSAv值排序的多个测试样本集上的MSE 值.可以看出,m=100 时,Dave_orig 模型在LSA值最高的前100 个测试样本上的MSE 值为0.363;m=80 时,LSAv指标取得的MSE 值为0.370,是所有m配置下的最高值.测试样本数量分别为1 000,2 000,4 000,5 000 时,LSAv与LSA指标取得的MSE 结果基本一致.
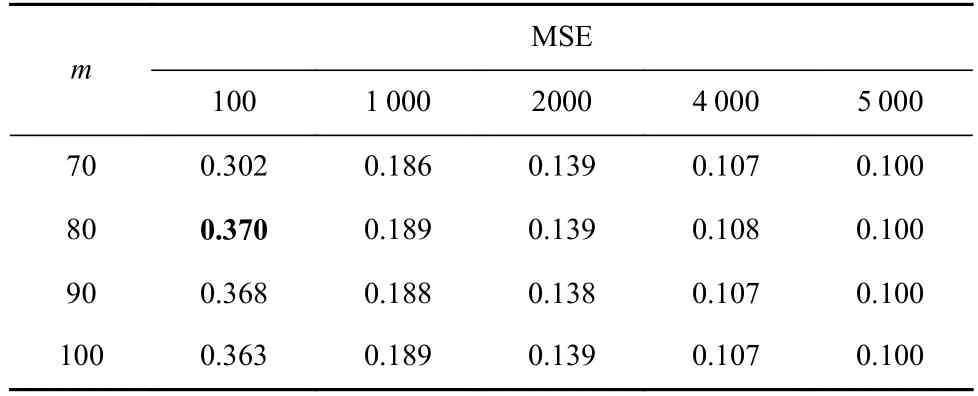
Table 5 MSE of Dave_orig Model on Selected Test Samples Based on LSAv Values表5 Dave_orig 模型在基于LSAv 值选择的测试样本上的均方误差
上述结果表明,利用重要神经元的输出值作为特征能够精准刻画样本间的差异,以此捕捉到异常的测试样本.利用深度神经网络可解释性算法LRP筛选出的对于决策结果影响较大的重要神经元能够刻画模型的决策逻辑,模型在差异较大的样本上的决策逻辑不同,则重要神经元输出值向量间的差异也就越大.测试样本的LSAv值和DSAv值越高,模型越难准确地预测,该样本更有可能是异常样本.在测试样本的真实类别标签未知的情况下,利用LSAv和DSAv指标可预先精准识别出可能被模型错误分类的异常样本.
4.3 改进的意外充分性的运行时间开销
图6 和图7 分别展示了待测DNN 模型在度量测试集的DSAv值和LSAv值的时间开销.从图6~7 中可看出,给定相同的测试数据集,LSAv指标的运行时间开销更小,性能更好.例如,在m=80 时,DSAv在ConvNet,LeNet5,LeNet4,Fashion-LeNet5 模型上的运行时间开销分别是LSAv指标的3.0,3.9,4.4,4.5 倍.其潜在原因在于度量单个测试样本的DSAv值时需要计算2 次样本间的神经元输出值差异,运行的时间开销更高.
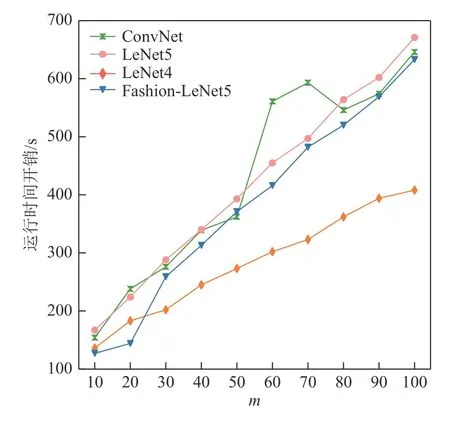
Fig.6 Time cost of measuring DSAv values with selecting different number of important neurons图6 选取不同数量的重要神经元度量DSAv 值的时间开销

Fig.7 Time cost of measuring LSAv values selecting with different number of important neurons图7 选取不同数量的重要神经元度量LSAv 值的时间开销
4.4 有效性威胁
1)内部有效性威胁.其主要体现在DeepSA 方法的实现、对比方法的实现以及实验结果分析评估的代码实现.为了有效减少这些威胁,DeepSA 方法在筛选重要神经元时采用了Alber 等人[29]开发的iNNvestigate 库,该库集成了多个DNN 模型可解释性技术,被广泛应用于模型可解释性相关的研究中,具备一定的可靠性.DeepSA 方法采用对比方法所贡献的开源链接上的最新版本源代码.此外,仔细检查了用于实验结果分析评估的代码实现,确保结果无误.
2)外部有效性威胁.其主要来源于本文所采用的深度学习数据集以及待测的DNN 模型.由于DeepSA 设计的联合优化目标仅适用于分类模型,本文仅在图像领域的分类模型上开展了测试样本生成方面的实验.后续还将进一步研究面向回归模型的CGF 方法.本文选取4 种公开图像数据集、5 个DNN模型开展实验,涵盖4 个分类模型和1 个回归模型,实验数据和被测模型被广泛应用于DNN 模型的测试中.之后的研究中还将选择任务更复杂的图像领域模型以及其他领域的模型作为实验对象,开展更广泛的研究.
3)结构有效性威胁.其主要来源于实验中DeepSA方法运行时指定的参数.DeepSA 方法运行时涉及到的主要参数包括:筛选的重要神经元占神经元总数的比例、样本生成迭代次数、学习速率、样本间距离阈值以及目标函数权值.本文根据相关CGF 方法中的参数推荐,对测试样本生成方面的参数进行了设计.在未来工作中,还将继续探究不同参数选择对方法效果和性能的影响.此外,选择待测DNN 模型的哪一隐藏层作为目标层也会对实验结果产生影响.针对不同的DNN 模型,实验中选取了多个隐藏层作为目标层,考虑到层数较深的隐藏层包含的神经元数量更多,且神经元的输出更能刻画样本复杂且多样的特征,DeepSA 重点考虑了层数较深的卷积层和全连接层.
5 相关工作
5.1 DNN 模型测试覆盖准则
软件的测试充分性是评价与保障软件质量的关键指标,传统软件测试已形成一套相对成熟的测试充分性度量准则,如分支覆盖、条件覆盖、MC/DC 覆盖等.然而,DNN 模型的构成机理和运行原理不同于传统软件,针对传统软件的测试覆盖准则难以直接运用于DNN 模型,研究学者提出了面向DNN 模型的结构性和非结构性测试覆盖准则,用于评估测试的充分性.测试集的覆盖率越高,越有可能揭露模型中隐藏的错误.
结构性覆盖准则用于量化DNN 模型内部结构被测试数据集覆盖的程度[15,19,30].Pei 等人[7]提出了首个针对DNN 的白盒测试覆盖准则—神经元覆盖,该准则量化测试样本激活的神经元数量与DNN 中神经元总数的比例.Ma 等人[15]从神经元的输出分布、活跃神经元的序列等角度,定义了神经元级和网络层级的多粒度覆盖准则,包括K多段区域神经元覆盖、神经元边界覆盖、Top-K神经元覆盖等.Gerasimou等人[13]设计了神经元重要性驱动的测试覆盖准则ІDC,在训练数据集上引入LRP 算法,获取对于决策结果贡献较大的神经元;通过聚类算法将每个重要神经元的激活值划分为簇;ІDC 准则分析重要神经元的激活值簇构成的组合被测试集覆盖的比例.Xie 等人[14]将DNN 隐藏层中对决策有关键贡献的神经元集合构成序列,作为模型的关键决策路径,分别从决策路径结构和决策路径中神经元激活值的角度,提出基于结构的神经元路径覆盖和基于激活值的神经元路径覆盖.
当前非结构性覆盖准则主要是指意外覆盖,Kim等人[9]从测试样本多样性的角度,衡量单个测试样本与训练集的差异,分析测试集的意外充分性值分布,基于此设计意外覆盖准则.本文聚焦DNN 模型的非结构性覆盖,以测试样本的意外充分性为引导,生成能够提升意外覆盖率的对抗样本.
5.2 测试样本生成
目前针对DNN 模型的测试样本生成方法分为2 类.第1 类是基于覆盖的测试样本生成方法,将传统软件测试的思路迁移到DNN 模型的测试中,通过对给定的种子样本进行变换,以最大化模型覆盖率为目标生成测试样本;第2 类是基于对抗的测试样本生成方法,通过向原始样本添加微小扰动的方式产生对抗样本,使DNN 模型产生错误分类结果[31-32].第1 类方法更关注生成的测试样本是否对模型内部结构实现了覆盖;第2 类方法则更关注生成的测试样本是否能够使模型产生错误输出.与对抗样本生成不同,DeepSA 以测试覆盖率为指导原则,构造变化微小、意外充分性值更高的测试样本,使得衍生测试样本集具有更高的测试覆盖率,旨在实现测试的充分性.本节主要介绍基于覆盖的测试样本生成的研究现状.
在基于覆盖的测试样本生成方法中,CGF 是当前的主要方法.Pei 等人[7]提出结合查分测试和神经元覆盖的测试样本生成方法,旨在最大化不同DNN模型输出结果差异和神经元覆盖率.Guo 等人[8]提出DLFuzz 方法,通过不断应用微小的扰动来对测试样本进行变异,最大化神经元覆盖以及原始样本和变异样本间的模型预测差异,同时定义了4 种神经元选择策略来选择更有可能提高覆盖率的神经元.Lee等人[33]在此基础上提出自适应的神经元选择策略,在测试样本生成的过程中,利用神经元的静态和动态特征,迭代生成神经元选择策略;通过计算选择的神经元的梯度对种子样本进行变异.Zhang 等人[34]提出CAGFuzz 方法,使用神经元覆盖率作为引导,利用对抗样本生成器生成对抗样本.代贺鹏等人[6]围绕测试数据生成、测试结果判定和覆盖分析3 个方面,对DNN 模型的CGF 方法进行了系统性地总结.本文提出的DeepSA 方法将测试样本生成建模为联合优化问题.不同之处在于,DeepSA 设置的2 个优化目标分别为测试样本的意外充分性和模型预测的类别概率向量间的差异.
6 总结与展望
本文将测试样本生成建模为联合优化问题求解,提出了一种意外充分性引导的深度神经网络测试样本生成方法DeepSA.该方法通过筛选对于决策结果重要的神经元,改进意外充分性指标;并利用该指标捕捉异常测试样本的能力,结合DNN 模型输出的类别间预测概率差异,设计联合优化目标,通过梯度上升算法产生扰动,对种子测试样本进行变异,迭代生成测试样本.本文在4 种图像数据集和5 个DNN 模型上对DeepSA 开展了有效性评估.实验结果表明,DeepSA 改进的意外充分性指标能够有效地捕捉异常的测试样本,并减少指标度量的时间开销;DeepSA 能够在生成对抗样本的同时提升意外覆盖率,优于典型的测试样本生成方法DeepXplore 和DLFuzz.在后续研究中,还将进一步利用意外充分性度量指标拓展至测试集优化[16,35]等任务中,基于意外充分性指标筛选测试子集用于模型重训练,以提升模型的准确率.后续还将改进DeepSA 方法,将其应用至回归模型上.
作者贡献声明:郭虹静提出方法框架,负责完成实验并撰写论文;陶传奇设计实验方案,提出指导意见并修改论文;黄志球提出指导意见.
