基于机器视觉的小型零件圆度测量*

丁哲文,张 瑞,,朱振伟,,赵华东,,刘丙康

(1.郑州大学机械与动力工程学院,郑州 450001;2.河南省智能制造研究院,郑州 450066)

0 引言

圆度误差是判断机械零件质量的重要参数之一,会直接影响零件的互换性、旋转精度、摩擦性及使用寿命等,甚至会影响到产品的使用寿命以及功能的实现。因次,快速、准确的评定圆度误差是检验圆形零件加工质量的重要标准之一。

目前,大部分制造厂商仍在采用接触式测量方法测量圆度误差,例如使用轮廓仪、三坐标测量机等测量工具,这些方法能够确保较高的测量精度,但成本高且对环境要求较高[1]。相比之下,机器视觉测量具有速度快、无损检测、可在线测量等优点。金守峰等[2]使用改进Zernike亚像素边缘检测获得边缘点,并使用最小二乘法评定圆度;吴德刚等[3]采用模糊遗传边缘检测获取边缘特征,并使用插值圆度检测算法测量出圆孔的半径等参数;朱丹丹等[4]使用Zernike算子定位边缘,并使用3准则剔除粗大噪声,然后利用最小二乘法评定圆度,其测量重复精度为9.6 μm。索振鹏等[5]利用灰度梯度边缘检测获取边缘后,使用最小二乘法计算圆度误差。韩宗旺等[6]对工件轮廓进行三维重构,提出一种自适应搜索逼近法评定圆度,其测量值与三坐标测量仪的平均有7.6 μm的误差。

传统的人工接触式方法用于小型零件圆度检测存在诸多问题,包括效率低、精度低、无法实时检测等问题。此外,现有研究中存在提取边缘特征的方法耗时长、计算量大,圆度评定方法精度低且原理不符合国际标准的最小条件等问题。为解决这些问题,本文提出了一种基于机器视觉的小型零件圆度测量方法。采用8邻域扩张算法划分感兴趣区域(region of interest,ROI),并结合多项式插值亚像素检测算法实现对小型零件边缘的精准定位,缩短计算时间,提高定位精度。在此基础上,结合改进区域搜索算法和最小区域法的几何结构,用于测量圆度误差,从而提高圆度误差测量的准确度。

1 边缘检测

在视觉检测过程中,边缘检测是决定测量精度的关键因素之一。

1.1 Canny算子边缘检测与ROI区域划分

常用的一阶边缘检测算子中,Canny算子因其抗干扰能力强、检测精度高而被应用广泛。本文采用Canny算子对待测零件的边缘进行初步定位,并以此边缘为基准进行8邻域扩张,将邻域范围内的像素点划定为感兴趣区域(ROI)。图1a为Canny算子检测出来的边缘,图1b展示了8邻域扩张后的ROI,之后进行亚像素边缘检测时只计算ROI内的像素点。这种方法可以显著减少计算时间,提高检测效率。

(a) Canny边缘 (b) 8邻域扩张

1.2 多项式插值的亚像素边缘检测

随着工业的快速发展,边缘检测要求的精度也不断提高,受到硬件限制的像素级已经无法满足高精度测量的需求,因此提出了不受像素尺寸大小影响的亚像素边缘检测。目前亚像素检测主要分为插值法、拟合法和矩方法3类[7]。在达到相同的精度下,插值法计算速度快,且对任意窗口尺寸都适用。本文采用多项式插值法进行亚像素边缘检测[8]。

二次多项式插值法原理为:

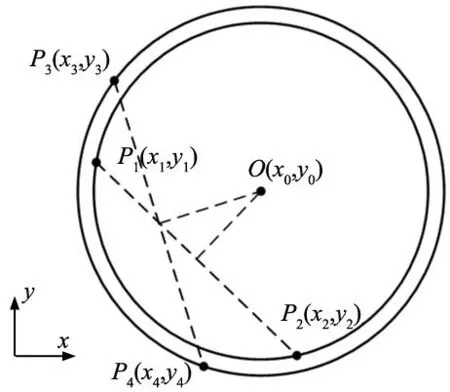
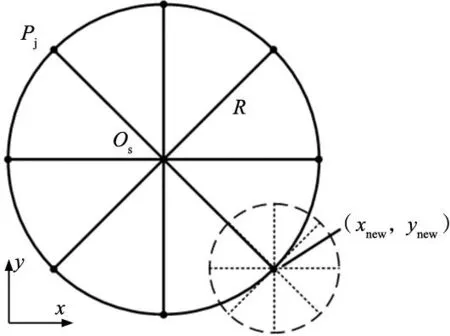
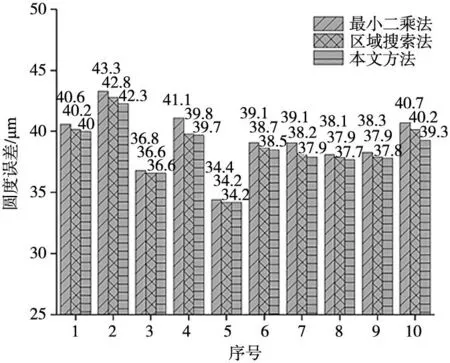
对相邻3点(x0,y0)、(x1,y1)、(x2,y2),满足y0

(1)

式中:f(x)为插值函数。

(2)

(3)

设边缘像素的梯度幅值函数为R(x,y)。如图2所示,R1、R-1、R0分别代表点M、N、O的梯度幅值。幅值最大的O点会被Canny算子检测为边缘点,但实际上在O点和M点之间存在P点,它的梯度幅值Rp大于其它点,因此P点能更适合表示边缘。

图2 相邻三点梯度幅值

对边缘点O(x0,y0)进行二次多项式插值,获得亚像素边缘点坐标P(xp,yp):

(4)

式中:D为相邻像素点到像素点的距离,θ为梯度方向与X轴正向夹角。该算法定义了8个方向模板,0°、45°、90°、135°、180°、225°、270°、315°、360°分别为模板的方向表示为图片实际边缘方向,顺着模板方向顺时针转90°为梯度方向。

算法流程为:

步骤1:ROI区域中的像素点与8个方向的模板进行卷积计算;

步骤2:卷积计算结果绝对值最大的值为该点的梯度幅值R0,并将对应模板的方向顺时针旋转90°获得梯度方向;

步骤3:沿着该点的梯度方向找到相邻点M和N,并计算两点梯度幅值,设为R-1和R1,根据R>R-1且R>R1进行判断,若满足条件则带入式(4)计算亚像素坐标,否则跳过。

2 圆度误差评定

圆度误差评定方法主要有4种,分别为:最小二乘法、最小外接圆法、最大内接圆法和最小区域法[9-10]。其中,最小二乘法是应用最为广泛的方法,但不满足国际标准定义的最小条件。最小外接圆法和最大外接圆法在确定轮廓的外接圆和内接圆时可能存在多个解,因此应用不便。最小区域法符合标准定义的最小条件,但属于无约束非线性化问题,难以直接求解[11]。本文针对小型零件的圆度评定,提出了一种通过改进区域搜索算法和最小区域法的几何结构相结合的方法。首先,利用最小二乘法拟合圆,将以最小二乘圆圆心为圆心,最小二乘圆度误差为半径的圆设为初始搜索区域,进行迭代,获得准圆心。接下来,利用最小区域法“2+2”几何结构和准圆心确定同心圆的内圆和外圆各两个点。最终,求解出圆度误差。

2.1 最小区域法圆度误差评定原理

圆度误差为实际轮廓两个最小同心圆的半径之差,计算公式为:

(5)

式中:(x0,y0)为最小区域圆心坐标,(xi,yi)为采样数据点,fmax为采样数据点到圆心的最大距离,fmin为采样数据点到圆心的最小距离,e为圆度误差。

最小区域法的几何结构为“2+2”形式[12-13]。该结构由采样点中4个非共线点决定,其中两个点位于同心圆外圆上,另外两个点位于内圆上,并且它们以最小的半径差值包围了所有的采样点。此外,外圆两点形成的线段和内圆两点形成的线段满足相交条件[14]。图3中P1(x1,y1)、P2(x2,y2)为外圆控制点,P3(x3,y3)、P4(x4,y4)为内圆控制点。由几何关系得,最小区域圆心O(x0,y0)为外圆控制点与内圆控制点连线的中垂线交点。

图3 “2+2”几何结构

线段P1P2中垂线公式为:

(x-x1)2+(y-y1)2=(x-x2)2+(y-y2)2

(6)

同理,线段P3P4中垂线式为:

(x-x3)2+(y-y3)2=(x-x4)2+(y-y4)2

(7)

联立式(6)～式(7),可得到4个控制点确定的最小区域圆心O(x0,y0),内圆半径Ri,外圆半径Ro分别为:

(8)

(9)

(10)

2.2 评定步骤

步骤1:通过最小二乘法[15]:

(11)

(12)

式中:n为数据点总数,(xi,yi)为样本数据点。

(13)

根据式(12)求出a、b、c后,根据式(13)获得最小二乘圆圆心Olsm(xlsm,ylsm)和半径rlsm。由式(5)获得初始圆度误差e0。

步骤2:将以Olsm(xlsm,ylsm)为搜索中心Os(xs,ys),e0为半径R的圆设为圆形搜索区域,并将圆n等分,获得搜索点Pj,其坐标由式(14)获得;

(14)

式中:(xs,ys)为当前搜索区域圆心,(xj,yj)为搜索点坐标,n为被等分数量。

步骤3:根据式(5)计算出搜索点的距离差值,并选出搜索点中最小距离差值enew,并记录其坐标(xnew,ynew)。如果搜索区域半径R小于指定的迭代精度ε,则停止迭代,转到步骤5。否则,进行下一步骤;

步骤4:如果enew≥e0,保持搜索中心Os不变,将R缩小10倍;如果enew

图4 圆形搜索区域示意图

步骤5:将迭代结束后的搜索中心Os设为准圆心,计算采样点到准圆心的距离,并选取距离最大值,次大值和最小值的采样点;

步骤6:将满足相交条件的采样点依次设为次近点,并根据式(5)和式(8),选出距离差值最小的采样点为次近点;

步骤7:根据式(8)～式(10),计算同心圆的圆心、内径Ri和外径Ro。并计算采样点到圆心的最小距离dmin和最大距离dmax,若dminRo,将同心圆的圆心设为搜索中心Os,并返回步骤3;若上述情况均不满足,则该采样点为次近点;

步骤8:计算圆心坐标和圆度误差值。

流程图如图5所示。

图5 圆度误差评定流程图

2.3 圆度评定方法验证

为了验证算法的可行性和准确性,采用文献[11]中圆度误差为0.002 mm的14个数据点和文献[10]中的39个数据点进行验证,本文方法取迭代精度ε=0.000 001,n=12并分别与最小二乘法、区域搜索法进行对比,对比结果分别如表1和表2所示。

表1 对14个数据点的数据对比结果 (mm)

表2 对39个数据点的数据对比结果 (mm)

从表1可以看出,基于区域搜索的圆度误差评定法比最小二乘法准确性更高,但仍有一些误差,并且该方法易受到步长和搜索方向的影响。通过本文方法测量得到的圆度误差值为0.002 mm,与标准值一致,这表明本文方法能够准确的检测的圆度误差。从表2可以看出本文方法求解出来的圆度误差值0.008 537 47 mm相较于其它方法更小。

3 实验分析

3.1 小型零件圆度测量系统

为了获得小型零件图像,建立了一个小型零件圆度测量系统,如图6所示,该系统主要包括工业相机、远心镜头、光源等。为满足检测需求,选用分辨率5472×3648的CCD工业相机,以获得高品质图像。光源采用LED背光光源,可以减少环境光线对采集图像的影响,并突出检测目标的轮廓边缘。系统的部分设备参数如表3所示。待测零件是外径环规。图7展示了外径环规图像,其中图7a为外径环规,图7b为工业相机拍摄的背光图像原图。在检测过程中,通过工业相机获取外径环规图像,实时传输到计算机进行处理。

表3 部分设备参数

图6 小型零件圆度测量系统

(a) 外径环规 (b) 背光图像原图

3.2 相机标定和图像预处理

相机获得的图像以像素为单位,若想获得零件的实际圆度误差,需要确定每个像素所代表的物理尺寸。通过相机采集20张左右在不同位姿下的圆形标定板图像后,利用张定友标定法,获得相机内参、畸变系数和圆心坐标等参数后,进行畸变矫正并求出像素当量k=0.008 755 mm/piexl。

图像矫正完成后,进行灰度化、引导滤波去除噪声以及基于Ostu的二值化阈值分割等预处理操作。图8和图9分别为滤波后的图像和二值化图像。

图8 滤波图像

3.3 圆度测量结果

为验证本文提出的测量方法的重复性和准确性,将外径环规的外圆作为检测目标。对外径环规的外圆重复测量10次,并在圆度评定时分别使用最小二乘法、区域搜索法和本文方法进行对比。测量结果如图10所示。

图10 测量结果

由图10和表4可以看出,本文方法的圆度测量结果平均值为38.4 μm,均方差为2.167 μm,均比区域搜索法和最小二乘法更小,并且重复精度为8.1 μm,说明本文方法测量的数据分布比较集中,波动小,重复性较好。

表4 测量结果对比 (μm)

4 结论

针对小型零件圆度测量存在的问题,搭建了基于机器视觉的小型零件圆度测量系统,通过Canny边缘检测、8领域算法划定ROI、多项式插值亚像素边缘检测提高了边缘定位的速度和精度。

提出了一种改进的圆度检测方法,结合了改进区域搜索算法和最小区域法的几何结构。该方法对采样点的分布没有特殊要求,能够有效测量的圆度误差,克服了区域搜索法等算法无法找到最小区域圆心的缺点。此外,该方法对迭代精度、步长等参数要求不高,提高了测量结果的稳定性。实验结果表明:本文方法测量结果的准确性相较于最小二乘法和区域搜索法有所提升,重复精度为8.1 μm,验证了本文方法的有效性,能够实现小型零件的圆度误差非接触测量。