基于FIR-Stacking的刀具磨损预测*
2024-04-29李备备陈春晓郑飂默
李备备,陈春晓,郑飂默,张 强
(1.中国科学院沈阳计算技术研究所,沈阳 110168;2.中国科学院大学,北京 100049;3.沈阳中科数控技术股份有限公司,沈阳 110168)
0 引言
铣床刀具是金属切削过程中经常使用的工具之一,其性能和寿命对铣削加工的质量、效率和成本具有直接影响[1]。然而,在使用过程中,刀具会遭受磨损和断裂等故障,这导致切削力增大、表面粗糙度降低、加工精度下降等问题[2]。因此,准确预测铣床刀具的磨损量对于保证加工质量、提高生产效率、降低维修成本以及延长刀具使用寿命具有重要意义。
目前,基于数据驱动的预测方法是预测刀具磨损量的研究热点之一。该方法通过分析刀具监测信号数据,利用信号学和特征工程的方法提取刀具磨损的退化特征,然后构建算法模型来完成刀具磨损量的预测[3]。基于数据驱动的预测方法的效果受到两个主要因素的影响:信号数据的处理和刀具磨损预测模型的选择。
在信号数据的处理方面,由于加工现场存在多种干扰源,采集到的数据常常包含大量噪声,因此对数据进行去噪处理至关重要[4]。常用的去噪方法包括时域的平均滤波、中值滤波,频域的低通滤波、高通滤波,以及时频域的小波去噪等[5]。然而,针对多轮铣削加工产生的多组信号数据,上述方法难以通过一组确定的参数获得良好的去噪效果。
在刀具磨损预测模型的选择方面,已有的研究中,朱云伟等[6]使用LightGBM模型预测刀具磨损状态,并通过遗传算法对模型进行调优。梁柱等[7]将支持向量机(support vector machine,SVM)和鲸鱼优化算法结合,实现了对钛合金加工刀具磨损状态的预测。李鑫等[8]则采用S变换提取特征,并利用隐马尔可夫模型识别刀具磨损状态。然而,这些研究只采用了单一传统机器学习模型,未考虑结合多种机器学习模型的优点。
综上所述,本文提出了一种基于自适应FIR滤波器和Stacking集成模型的刀具磨损预测方法。该方法采用自适应FIR滤波器解决工业噪声问题,并利用Stacking集成模型解决单一传统机器学习模型预测效果不佳的问题。通过在实际数控机床铣刀数据集上的实验应用,与其他方法进行对比,实验结果表明本文提出的方法相对于其他方法具有更高的预测准确性。
1 模型提出
1.1 FIR滤波
FIR滤波是基于有限长冲激响应的数字滤波器,其特点是结构简单、易于实现和稳定可靠。与无限长冲激响应的IIR滤波器不同,FIR滤波器可以实现线性相位响应,因此在数字通信、语音处理、音频处理等领域得到广泛的应用[9]。
在FIR滤波器中,输入信号从上一个时刻的输入值和滤波器中的状态序列计算得到。输出信号的计算是在输入信号通过滤波器后,由滤波器的输出序列组成。
FIR滤波器的设计可以通过两种方法实现:窗函数法和频率采样法。其中,窗函数法中又以Kaiser窗函数最为常用。Kaiser窗函数通过设定窗函数的形状参数β来实现对滤波器的频率响应进行调节,较大的β值会导致更陡峭的衰减,但可能会引入较宽的过渡带,较小的β值会产生较宽的主瓣,但过渡带可能较窄。它的特点是具有平滑的衰减特性,从而可以在带阻滤波器等需要高衰减的场合中得到较好的滤波效果。
1.2 Stacking集成模型
Stacking集成模型是集成学习中一种常用的模型结构。Stacking不仅可以用于提高模型的表现能力,也可以用于模型融合以及特征选择等任务。该算法的核心思想在于将不同的模型进行串联,使得每个模型的预测结果成为下一个模型的输入,以此提高模型的性能和稳定性[10]。
Stacking将多个基模型组合成一个更高层次的模型,在预测时,将每个基模型的预测结果作为新特征输入到元模型中进行训练和预测。元模型可以是任何机器学习模型,典型的包括线性回归、Lasso回归、Ridge回归等。
Stacking的训练过程可以分为两个阶段,如图1所示。首先,在第1阶段中,使用交叉验证将输入数据划分为多个折,然后在每个折中训练多个基模型。这些基模型可以是不同的回归器,例如SVR、LightGBM和MLP等。第2阶段中,使用第1阶段的基模型在训练集上生成新的特征,并且使用这些特征训练元模型进行最终的预测。

图1 Stacking的训练过程
Stacking集成模型是一种强大的机器学习融合模型,它已被广泛应用于各种学习任务。通过将多个基模型融合在一起,Stacking可以显著提高模型的预测性能和稳定性,同时也能够进一步挖掘数据中的信息,使模型更具有表现力。
1.3 LightGBM模型
LightGBM是一种基于决策树算法的快速、高效、分布式梯度提升框架[11]。其核心原理是采用直方图算法对连续特征进行离散化,减少内存压力和计算负担,提高训练速度。在构建决策树时,LightGBM利用基于梯度的one-side相对误差来分割数据,保证分区质量,提高了预测精度。
1.4 SVR模型
SVR是一种基于SVM的非线性回归方法[12]。SVR的核心原理是通过在特征空间中找到一个能够将样本点映射到高维空间的决策函数,使得该函数与样本点的距离最小。在SVR中,使用参数C来控制模型的容错率,同时通过引入核函数将非线性问题映射到高维空间,进行复杂的非线性回归任务。
1.5 MLP模型
MLP是一种基于人工神经网络(artificial neural network,ANN)的前馈神经网络[13]。MLP的核心原理是将输入层、隐藏层和输出层连接起来构成网络模型,通过反向传播算法进行网络训练,进而实现分类或回归任务。在MLP中,每个节点用sigmoid、tanh、relu等激活函数进行非线性变换,将输入信号传递到下一层节点。隐藏层的存在使得MLP具有处理非线性问题的能力,而输出层则根据任务需求确定其节点数量和激活函数。
1.6 Lasso模型
Lasso是一种基于L1范数正则化的线性回归算法[14]。Lasso的核心原理是通过在普通最小二乘的基础上加入L1正则项,实现变量选择和模型压缩。在Lasso中,L1正则化项通过对回归系数进行惩罚,将某些回归系数压缩到0,从而可以进行变量选择,避免模型过拟合。
1.7 基于FIR-Stacking的刀具磨损预测方法
针对工业噪声问题,使用基于Kaiser窗函数的FIR滤波器,设计一个带阻滤波器进行信号数据的去噪。为了保证设计的带阻滤波器可以尽可能的去除噪声频带,并且保留原有信息,本文使用贝叶斯优化算法对滤波器的阶数、截止频率、带宽和Kaiser窗函数的β值组成的参数空间进行参数寻优,以最大化信噪比为目标,最终得到最优滤波器。信噪比的公式如式(1)所示。
(1)
式中:Ps是信号的功率,Pn是噪声的功率。
针对单一传统机器学习模型预测效果不理想的问题,设计一个Stacking集成模型。由于Stacking集成模型的基模型需要选取强回归模型并且模型之间存在差异性,才能使得集成模型的效果变好。因此通过对多种回归模型的实验,最终选择使用LightGBM、SVR和MLP作为集成模型的基模型。Stacking集成模型的元模型一般来说需要选择比较简单的回归模型,这样可以避免集成模型过拟合,因此本文通过对线性回归、Lasso回归和Ridge回归3种简单回归模型的实验,最终选择效果最好的Lasso回归作为元模型。
综上所述,本文设计了一种基于自适应FIR滤波器和Stacking集成模型的刀具磨损预测方法,算法流程如图2所示。
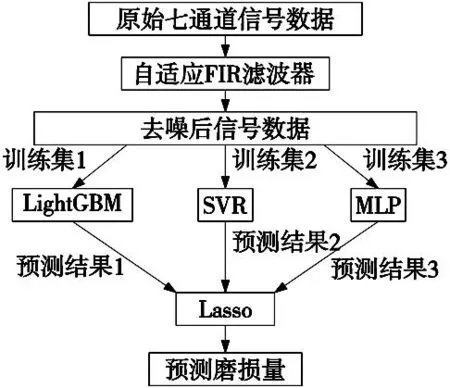
图2 FIR-Stacking算法流程图
2 实验验证及结果分析
2.1 实验数据集介绍
为了验证本文所提刀具磨损预测方法的有效性,选择刀具磨损预测竞赛的公开数据集进行实验,实验环境如图3所示。该数据集使用Roders Tech RFM760高速数控机床,采用三槽球头硬质合金铣刀,在HRC52硬度的不锈钢上进行了铣削试验,试验条件如下:主轴转速为10 400 r/min,进给率为1555 mm/min,径向切深为0.2 mm,轴向切深为0.125 mm。试验过程中,使用力、振动和声发射传感器进行数据采集,采样频率为50 kHz,共采集了7个通道的信号,包括切削力信号(3个方向)、加速度信号(3个方向)和声发射信号。每完成一次工件表面铣削,使用莱卡MZ12型号显微镜进行离线测量刀具磨损量,直到刀具达到磨钝标准停止实验。实验过程中进行了315次切削试验,使用了6个刀具进行了6组试验,得到了标记为C1、C2、C3、C4、C5和C6的6个数据集。
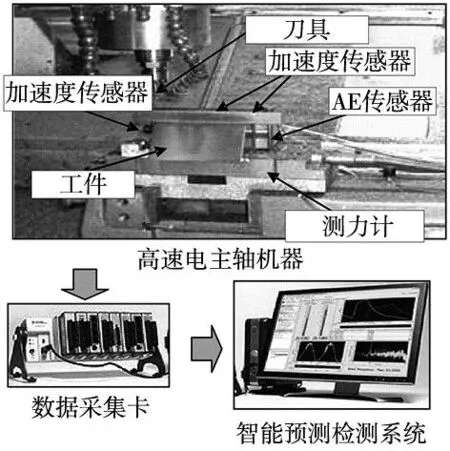
图3 铣削过程中刀具监测实验环境
本实验将选取带有磨损值标签的C1、C4和C6数据集作为实验数据集,使用7维信号数据作为实验数据,并取其中80%作为训练集,20%作为测试集。
2.2 数据异常值剔除
在刀具加工过程中,因为存在进刀(刀具下降加工)和出刀(刀具上升移动)操作,导致产生了一些不同于正常信号的波动,这些波动可以被视为异常值,需要进行剔除。通过对信号的观察和分析,本文决定将信号数据的前10%和后10%视为异常值,并进行剔除。剩余的信号数据具有较好的稳定性和连续性,更适合用于后续的实验研究。另外,由于铣刀每轮加工产生的信号长度不同,因此我们在截取后的信号数据中取长度为100 000的信号数据进行后续实验。
2.3 数据去噪
在工业加工中,由于存在大量不知名噪声,这些噪声会对刀具磨损预测的准确性和稳定性造成不良影响,因此去噪处理成为必要的步骤。
为了解决噪声问题,使用本文设计的自适应FIR滤波器进行去噪,并且将它与原始多源信号数据进行比较,如图4所示,是C6数据集第1轮加工中X方向振动信号的滤波前后对比图。由图4可以看出,原始信号存在一个信号突变,它出现的原因可能是现场干扰噪声、颤振等,但是经过自适应FIR滤波器滤波之后,信号突变就被滤去了,并且信号变得平滑许多。

图4 滤波前后对比图
后续的实验结果也表明,经过本文的自适应 FIR 滤波器处理后的信号数据与原始信号数据相比,预测准确性更高。
2.4 数据增强
本文使用的刀具数据集,单把刀具只有315个样本,由于样本太小容易造成模型过拟合等问题,从而严重影响模型预测结果。因此,我们采用了数据增强技术,将原始信号数据切分成10份,对每份数据分别进行特征提取,将单把刀具的样本量提升至3150个,提高了数据的多样性和数量,进而提高了模型的准确性和鲁棒性。
2.5 数据特征提取
数字特征提取是信号分析和处理的重要一环,其目的是从原始信号中提取有用的信息,用于后续的建模和分析。在本文中,我们使用傅里叶变换(fourier transform,FT)得到信号的频域信息,使用短时傅里叶变换(short time fourier transform,STFT)得到信号的时频域信息,并对信号的时域、频域和时频域信息分别提取了10类常用的统计量,包括均值、偏度、峰度、标准差、能量、均方根、峰峰值、波形因子、脉冲因子和裕度因子,上述10种统计量的计算方法如表1所示。

表1 信号数据常用统计量计算方法
这些统计量可以反映出信号数据在时域、频域和时频域不同方面的特点和变化规律,对于刀具磨损的分析和预测具有重要的作用。其中均值、标准差和能量是信号特性的基本统计量,可以反映出信号的中心趋势、波动程度和信号强度;偏度和峰度可以描述信号数据的非对称程度和峰态;均方根和峰峰值可以反映信号的幅值大小和变化范围;波形因子、脉冲因子和裕度因子可以反映信号数据的形状特征和变化规律,对于提高刀具磨损预测准确性具有重要的影响。
在本文中,通过对于单维信号的特征提取,获得时域、频域和时频域共计30种特征,然后通过将7维信号的特征进行拼接处理,获得共计210种特征。
2.6 数据降维
数据降维是在保留原始数据特征的同时,尽可能减少数据特征的数量,以达到减少计算负担和提高模型性能的目的。在本文中,采用Pearson相关系数进行特征选择,筛选出相关系数大于0.2的特征,作为本文所提模型的输入。
2.7 实验结果对比
为了验证本文所提方法的预测性能,从数据和模型两方面做出对比。在数据方面,分别对数据进行了不去噪、使用自适应FIR滤波器去噪两种预处理方式,以得到不同干预下的数据集,从而探究不同预处理方式对模型预测效果的影响。在模型方面,采用了Stacking集成模型、LightGBM模型、SVR模型和MLP模型,对比不同模型的刀具磨损量预测准确性。在实验中,我们使用平均绝对误差(mean absolute error,MAE)和均方根误差(root mean square error,RMSE)作为指标来评估模型的预测准确性。MAE与RMSE的公式如式(2)、式(3)所示。
(2)
(3)
式中:ytest是测试值,ypred是预测值。
表2展示了不进行去噪处理的情况下,各个模型在样本集上的MAE。从结果可以观察到,与3种基本模型相比,本文设计的Stacking集成模型表现出更低的MAE值。
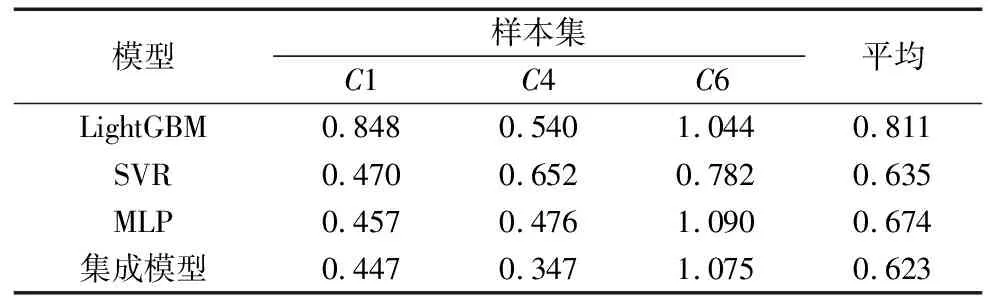
表2 不去噪处理方式下各模型在样本集上的MAE
表3展示了不进行去噪处理的情况下,各个模型在样本集上的RMSE。从结果可以观察到,与3种基本模型相比,本文设计的Stacking集成模型表现出更低的RMSE值。

表3 不去噪处理方式下各模型在样本集上的RMSE
表4展示了使用自适应FIR滤波器去噪的情况下,各个模型在样本集上的MAE。从结果可以观察到,与3种基本模型相比,本文设计的Stacking集成模型表现出更低的MAE值。

表4 自适应FIR滤波处理方式下各模型在样本集上的MAE
表5展示了使用自适应FIR滤波器去噪的情况下,各个模型在样本集上的RMSE。从结果可以观察到,与3种基本模型相比,本文设计的Stacking集成模型表现出更低的RMSE值。
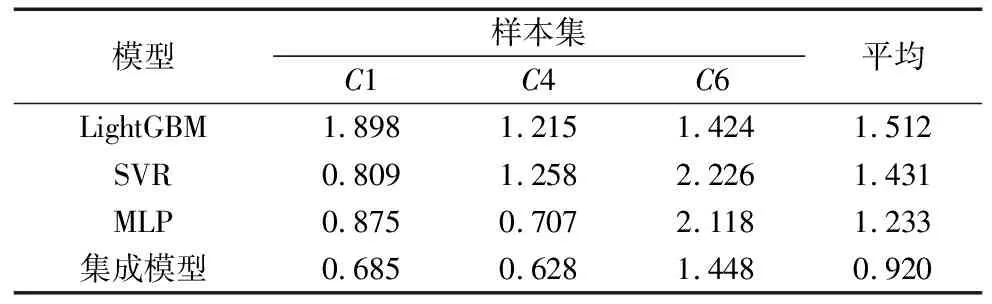
表5 自适应FIR滤波处理方式下各模型在样本集上的RMSE
综合表2~表5的结果可以看出,在数据预处理方面,使用自适应FIR滤波器去噪相比于不进行去噪效果更佳,尤其是在C6数据集上效果提升很大。并且在各种方法中,C6数据集的MAE和RMSE都要明显低于C1数据集和C4数据集,这就说明C6相对于另外两把刀具数据包含了更多的噪声,从而导致预测效果不好,而本文提出的自适应FIR滤波器可以有效的过滤C6数据集中的噪声,提高它的预测效果。在模型方面,Stacking集成模型相对于LightGBM模型、SVR模型和MLP模型具有更好的预测效果。
图5~图7是基于自适应FIR滤波器和Stacking集成模型预测方法在C1、C4、C6测试集上的预测图。
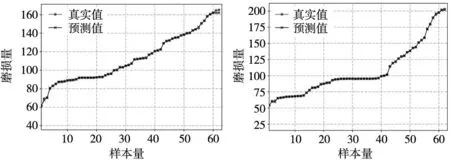
图5 C1刀具磨损量预测曲线

图7 C6刀具磨损量预测曲线
从表4、表5和图5~图7可以看出,本文所提的基于自适应FIR滤波器和Stacking集成模型的刀具磨损预测方法在样本集上的平均MAE是0.459,平均RMSE是0.920,预测准确性很高。
3 结论
本文提出了一种基于自适应FIR滤波器和Stacking集成模型的刀具磨损预测方法,该方法能够有效地解决传感器信号存在噪声和单一传统机器学习模型预测准确性不理想的问题。通过在铣刀加工数据集上的对比实验,验证了本文所提预测方法的可行性和有效性,并且相较于其它几种预测方法,本文所提方法在刀具磨损预测精度上有了较大的提高。
目前,本文只是利用Stacking集成模型集成了几种不同的机器学习模型,在后续的研究中可以考虑选择机器学习模型和深度学习模型作为基模型,从而结合两类模型的优点,并进一步提高刀具磨损预测准确性。
