基于平面共轭对数的弧齿锥齿轮齿面设计研究*
2024-04-29付雁博田国富
付雁博,田国富
(沈阳工业大学机械工程学院,沈阳 110870)
0 引言
弧齿锥齿轮因具有较高的齿面接触的重合度而可以实现较为优秀的传动平稳性和承载能力,同时具有能够实现交错轴及相交轴传动的特点,因此被广泛应用于机械的传动机构中,如作为汽车或轮船和航空航天的载具中的重载传动部件。弧齿锥齿轮因为其齿面形状的复杂,在进行参数设计以及建模的过程中往往会出现曲面精度不足等问题造成后续仿真实验结果的数值偏差。实现弧齿锥齿轮对中的大小齿轮的凹凸面、齿根与齿顶,以及齿根过渡曲面的参数设计与之后的建模是实现轮齿使用强度及寿命等性能指标仿真分析的重要基石。
LITVIN、李兆文等[1-2]在研究中利用展成法的原理对弧齿锥齿轮齿面进行参数设计,通过刀具外侧方程和刀尖圆角方程通过齿面的展成加工原理所进行的齿面特征点进行计算;薛德余等[3]基于展成法,利用计算机模拟实际的弧齿锥齿轮加工过程,并反向推导出齿轮工作曲面的凹凸面点位,进而生成齿槽。
利用展成法等理论的参数设计方法所得出的数学建模,在计算齿面点时往往会因为齿轮或者加工过程中刀具或加工机床等的参数设置差异使得结果齿面精度并不理想,同时对于齿根过渡曲面大多采用了近似取值,在实际应用中往往需要通过齿面拟合等方法进行矫正,且计算过程复杂,其程序生成齿面点时过程繁琐,存在较大误差,不利于提高弧齿锥齿轮参数建模的效率和精度。
随着研究发展,利用球面渐开线齿廓进行设计计算逐渐在弧齿锥齿轮设计与制造中获得重视[4-6]。利用球面渐开线理论设计的工作曲面的齿面齿形可以实现传动过程中一堆共轭曲面的正确啮合,且基于球面渐开线的设计具有轴角误差补偿能力[7]。
近几年来,有学者基于共轭曲线理论发展出了新的弧齿锥齿轮网格划分理论[8],为利用平面对数几何元素引入到齿面生成中提供了理论依据;ZHOU等[9]提出了一种新型的计算齿轮齿面点位的方法,以此来获得弧齿锥齿轮近似等距点与曲线;为了避免制造和装配的空间及角度误差造成的对中性误差,有学者通过调整机床设置获得最佳齿面进行了尝试[10-11]。目前基于球面渐开线的弧齿锥齿轮齿形设计仍有改良的空间,为了使球面渐开线理论在弧齿锥齿轮设计中得到更加充分的应用,本文利用平面共轭对数进一步提升工作齿面的精度。
1 利用空间共轭曲线改进的弧齿锥齿轮成形原理
理论上,弧齿锥齿轮中本身具有的球面渐开线是具有类似于轴角误差补偿等能力的,因此若是根据展成法等理论进行弧齿锥齿轮的齿形设计,其生成齿廓在实际建模和虚拟装配中往往会出现对中性误差等等,需要在后续的实验中不断矫正以达到相对准确的精度与平稳的接触应力变化。故本文提出以球面渐开线理论为基础,并基于平面共轭对数进行弧齿锥齿轮基于共轭曲线的改进设计理论与方法。
1.1 改进的弧齿锥齿轮设计理论
为了使齿轮啮合时能够沿着啮合线始终保持较高的接触强度,故本文在球面渐开线齿形设计理论的基础上,利用共轭曲线设计,如图1所示,为球面渐开线的形成原理。在从弧齿锥齿轮的基础齿面所展开的盘型平面上,盘形平面所处的坐标系沿着基圆锥的母线相连并相切。处在盘形平面边缘上的动点P在球面渐开线上的任意一个位置其与基圆锥的顶点O,即盘形平面坐标轴的原点的距离相等,且动点P在空间活动的迹为球面渐开线,利用平面对数在弧齿锥齿轮啮合传动的共轭曲线上利用法向截面的圆弧齿形上建立新的齿面。

图1 平面对数在球面渐开线锥齿轮设计中的引入
弧齿锥齿轮的齿面即可根据从同时存在于基圆锥底部与圆盘平面的交点来进行确定,其平面对数rlog可表示为:
rlog=[0ecotβ·θsin(φsinδb)ecotβ·θ(φsinδb) 1]T
(1)
式中:δb为基圆锥轴线OO0与圆盘坐标系中yc轴的夹角,同时也为基圆锥母线与基圆锥轴线的夹角。所以当基圆锥与圆盘平面发生相对滚动时,两者的坐标系的转换为:
(2)
故引入平面共轭对数后的弧齿锥齿轮的球面渐开线齿廓的对数齿面转化可表示为:
[x1y1z11]=M1c·[x1y1z11]T
(3)
在图2中设动点P在球形渐开线的另一位置时处于点过点Q。作与圆形盘面所处坐标系原点O0及基圆锥底面圆心O这两者连线OO0保持垂直关系的平面,与轴线OO0相交于K点,与基圆锥母线相交于N点。根据三角函数关系,在直角三角形O0NK、O0NP和O0PM中,可知:
(4)

图2 球面渐开线的形成原理
且根据球形渐开线的性质可知:
(5)
继而得出:
(6)
得到在球面渐开线上的任何位置上的动点P所在的偏角为:
(7)
式中:δk为动点P在运动时的所对应的基圆锥母线与圆锥轴线的夹角。
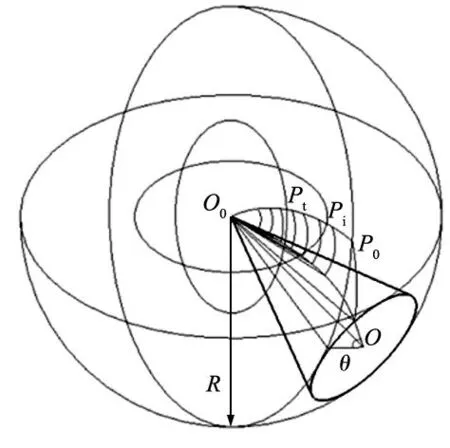
图3 齿面形成原理图
1.2 确定弧齿锥齿轮的齿面啮合曲线
由图4所示的柔性坐标系中,S0和Sp是与水平面相连,其中点O1、O2、O0、Op是弧齿锥齿轮中的两个齿轮的顶点重合。z0轴穿过小轮的轴线,zp则穿过大轮的轴线。x0与γp·φ1和φ2重合,其中γp·φ1和φ2(φ2=i21φ1)表示小轮和大轮在一定时间段内相对于原位置的转动角度,Γ1和Γ2分别表示大小齿轮的球面渐开线共轭曲线。

图4 齿轮传动啮合的基本坐标系
坐标轴S1到坐标轴S2的转换矩阵可表示为:
M21=M2pMp0M01=
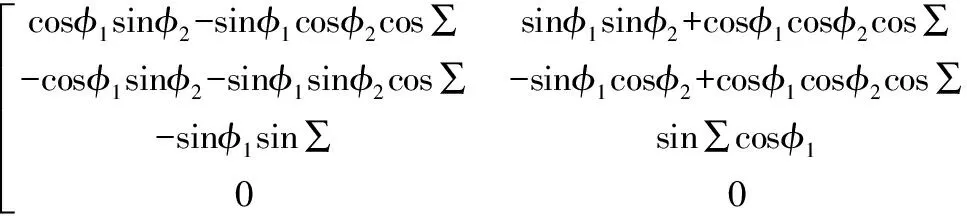
(8)
基于球面渐开线建模的弧齿锥齿轮中的齿面接触路径可表示:
(9)
式中:c1与c2的值由边界条件所确定。
对于小轮来说,接触迹线可表达为:
rΓ1=[xΓ1(φ)yΓ1(φ)zΓ1(φ) 1]T
(10)
齿面上进行网格化处理之后曲线的相对速度可表示为:
v12=ω1×rΓ1-ω2×rΓ2
(11)
式中:rΓ1、rΓ2和ω1、ω2分别表示为小轮和大轮在坐标轴S1中的位置矢量以及相对角速度。
在接触迹线rΓ1中存在的单位法向量nΓ1需要满足与起始球面渐开线方向重合,则有:
(12)
nΓ1·v12=0
(13)
继而推导:
(14)
故共轭曲线Γ2与共轭曲线Γ1相切等性质可以总结为:
(15)
2 弧齿锥齿轮的齿面生成
在弧齿锥齿轮建模程序中,将建模过程分为齿轮工作曲面、大小齿端曲线以及齿根过渡部分3个部分。
2.1 生成弧齿锥齿轮工作齿面
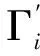
(16)

图5 弧齿锥齿轮齿面生成原理
式中:单个齿面凹凸面的法向横截面的齿廓可表示为:
(17)
所以在以球形渐开线为设计基础的弧齿锥齿轮的齿面选择两对共轭曲线,一对在节锥角上方,另一对在下方,通过此方法可以生成齿轮的凹凸面。根据变换矩阵M21可以得到图5中两个向量αΓi与nΓi:
(18)
2.2 大小齿端曲线的确定
大端的曲线分为齿顶、齿根进行求解。其中齿顶部分用以下公式进行确定:
(19)
进行齿根计算时则需要公式:
(20)
式中:ρ表示矢径。对于同一齿的另一面的计算,则需要替换以下参数:
(21)
式中:φf表示齿厚。
对于小端部分的曲线求解的方程可表示为:
(22)
式中:Δφ表示小端相对于大端的偏角。
2.3 齿根过渡曲面参数的确定
齿根过渡曲面需要根据以基于球面渐开线设计中的渐开线与基圆锥的参数进行单独设计。根据设计齿轮的参数不同,也会随其球面渐开线中的基圆锥的底面半径的变化有关。在半径值大于齿根圆的半径时,根据选用的刀盘圆角的半径以及考虑刀具与被加工齿轮之间是否存在侧面间隙和齿顶间隙,有公式为:
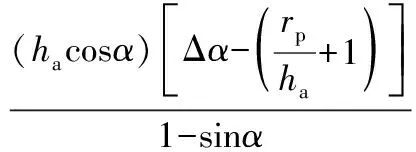
(23)
式中:
(24)
式中:α为弧齿锥齿轮参数中的压力角,ha为齿顶高,rp为节圆半径。
如果加工刀具与齿轮之间存在侧面间隙或齿顶间隙时,则需要将以下参数进行替换:
(25)
式中:jm表示为最大间隙。
若基圆锥底面半径小于齿根圆半径,根据文献[12]可使用变半径倒圆角的计算来进行齿根过渡圆角的处理,有以下公式进行推算:
rt=0.3m
(26)
3 基于球形渐开线设计的弧齿锥齿轮建模与网格划分实例
3.1 弧齿锥齿轮三维建模
本次建模选取的弧齿锥齿轮参数如表1所示。

表1 弧齿锥齿轮主要参数
由结合之前公式及理论所设计出的程序得出单个齿槽的齿面点阵,并利用三维绘图软件中的点线连接以及放样曲面功能沿着由点阵列所组成的曲线进行曲面组成,如图6所示。根据弧齿锥齿轮设计手册,可以确定弧齿锥齿轮毛坯的尺寸,并进行绘制。使用所得到曲面进行放样切除,并利用圆周阵列功能按照齿数进行布置,得到如图7所示的弧齿锥齿轮大轮模型。

图6 弧齿锥齿轮单齿槽的凹凸面及齿顶面
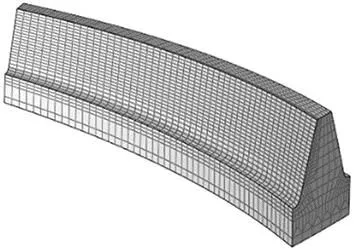
图8 弧齿锥齿轮单齿网格划分模型
3.2 弧齿锥齿轮仿真前处理的网格划分
为了对弧齿锥齿轮传动副进行精确的有限元分析,需要对由上述步骤所生成的弧齿锥齿轮进行网格划分以作为前处理环节。
为了能够实现提升仿真速度以及提高后续的仿真精度,需要对弧齿锥齿轮对接触面的工作曲面和齿根过渡曲面进行特别加密。根据实际承载接触分析或动力学仿真时情况总结出需将弧齿锥齿轮副中进行主要接触的工作曲面和相对应的齿根部分的网格数量进行相应的增加,而对齿轮接触仿真结果影响很小的齿坯部分的网格适当减少,加快仿真后处理的效率。
4 仿真算例
在仿真中,赋予网格材料属性为20GrMnti,材料密度7.8×10-9t/mm3,设置杨氏模量和泊松比分别为E=205 GPa和λ=0.3,有限元模型及经过接触面定义以及旋转耦合约束后的建模如图9所示。
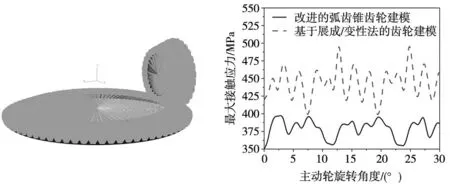
图9 弧齿锥齿轮耦合定义模型
设置基于展成法弧齿锥齿轮程序[13]作为对照组,给予作为主动轮的小轮旋转的一定旋转角速度,对两组被动旋转的大轮施加同样的抵抗旋转的力矩,对弧齿锥齿轮装配体进行接触强度的分析,得到如图10所示的多组小轮进入啮合到脱离这个时间段内接触应力变化的数据。可以看到引入平面对数进行改进的球面渐开线弧齿锥齿轮建模在实验仿真中具有更高的接触强度,其中改进后的小轮凹面最大齿面接触应力图如图11所示。
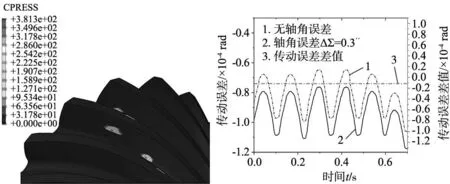
图11 改进后的小轮齿面应力云图
为了验证此次改进的弧齿锥齿轮建模在实际仿真中因制造与装配而产生的轴角变化ΔΣ导致的传动平稳性上的变化,设置装配之后的小轮相对于理论位置的轴角变化值ΔΣ,小轮转角设置为1.3 rad,运行时间为1 s,摩擦系数为0.15。根据传动误差公式计算得到如图12所示在轴角误差装配误差下的传动误差函数。
5 结论
本篇研究在原先球面渐开线的弧齿锥齿轮参数建模中引入几何元素中平面对数等设计与计算方法对弧齿锥齿轮的曲面建模进行了改进,最终得到结论如下:
(1)结合数学程序设计以及三维制图软件的应用,使建模过程的复杂程度大幅降低,减少了进行复杂运算的时间,为之后的接触分析和动态分析提供了精确的建模和网格划分前处理的条件。
(2)改进的设计提升了基于球面渐开线理论设计的弧齿锥齿轮对于装配时存在的对中性误差之一的轴角误差的适应能力,在存在轴角误差的情况下整体的加载传动误差变化趋势较稳定,展现了球面渐开线齿面设计理论当中对弧齿锥齿轮在传动过程中轴角补偿的能力。
(3)设计的弧齿锥齿轮在同样的仿真条件下,其接触应力低于传统设计的弧齿锥齿轮,且接触应力变化更加稳定,体现出了更高的接触强度。
