基于应变测试矿用汽车车架结构优化设计分析

李 伟，杨 晨

（郑州科技学院机械工程学院，河南 郑州 450064）

1 引言

矿用汽车中的铰接式车辆主要应用于矿山运输，承载较大，同时由于道路环境限制，车架常常采用铰接式布置形式。铰接式布置可以有效缩短转弯半径，提升转向能力，而被广泛应用于巷道运输[1]。此类车辆通常是空载-装载-满载-卸载等的往复工作循环，此种形式的工作，对车架形成较大的冲击载荷作用。因此，设计过程中，需要对车架，尤其是后车架和货箱的应力分布进行分析，根据结果对设计进行优化，以提升设备的安全性。对此，进行研究，为实际设计提供参考。国内外学者对此进行了一定研究：文献[2]应用NASTRAN对铰接式车架的受力进行分析，并对应力较大区域进行优化设计；文献[3]应用ANSYS对超重型铰接车进行有限元分析，获得车架的自振频率和振型；文献[4]应用ANSYS对铰接式车架的承载特性进行分析，获得较为精确的结构性能参数和受载结果参数；文献[5]利用ANSYS∕LS-DYNA对有货箱的装卸过程进行分析，以获取最佳的补丁板结构设计。

针对某铰接式矿用汽车为研究对象，选取不同运行工况下，对后车架和货箱的受力情况进行分析；基于有限单元法建立后车架的分析模型，以分析结果进行加载和边界设置，分析四种典型工况下，车架的受力情况，获取不同工况的应力最大点和应力集中区域；选取结构、材料、焊接等方法，对应力较大和集中区域结构进行优化设计，并对修正后的模型进行分析；基于实车测试，选取极限工况，在应力较大和集中区域布置传感器，获取实测结果值，并与仿真结果进行对比分析，以验证仿真分析和优化设计的可靠性。

2 后车架承载分析

矿用铰接式车辆满载卸货工况，如图1所示。此类车辆的组成结构主要包括以下部分：前车架、后车架、铰接装置、举升机构、货箱等[6]。整车满载货物为25t，前车架11t，后车架5t，整车尺寸为（9.15×2.96×2.54）m。

图1 车辆举升状态Fig.1 Vehicle Lifting Status

2.1 满载运行

车辆满载货物为25t，此时，货箱的主要重量集中在与车架的接触面和铰接点位置[7]，此时货箱未举升，货箱和车架受力，如图2所示。

图2 满载运行工况受力Fig.2 Stress Under Full Load Operation Condition

图中：G—总重量；R—货箱与车架接触部位的支撑力；N—货箱与车架的后铰接轴销处的力。

对货箱的力学模型，得到如下的平衡方程：

R点合力矩平衡，则：

此时，车架在水平方向不受力。

对R2作用点取矩，则：

式中：N3和N2，R和R3—互为反作用力，假设R4=R5。

2.2 举升工况

此时，车辆满载货物，而处于停车状态，油缸开始把货箱举升起瞬间的货箱和车架受力，如图3所示。

图3 举升工况受力分析Fig.3 Force Analysis of Lifting Condition

图中：F—货箱与举油缸的作用力。

对货箱的力学模型，得出如下的力平衡方程：

重心点力矩为0，则，可得：

其中，F1=Fcosa，F2=Fsina。

根据受力平衡，则：

对R2作用点取矩，则：

对F3作用点取矩，则：

上式中假设P1=P2，R1=R2。由上面的方程可以求解出：P2和R2、R4、R5。

2.3 制动工况

车辆满载运行，发生制动时，车辆匀速运行的限速为26km∕h，根据载重情况，可得最大制动距离为9.12m。此时的受力情况，如图4所示。

图4 制动工况受力分析Fig.4 Force Analysis of Braking Condition

根据达朗伯原理，Fg为惯性力，则：

对R作用点取矩，则：

由达朗伯原理，可知：

由上面的方程可以求解出：P1、P2、R1、R2、R4、R5。

2.4 满载上坡

车辆满载运输时，爬坡工况，运行的坡度角为15°[8]，此时，货箱和车架的受力分析，如图5所示。

图5 上坡工况受力分析Fig.5 Force Analysis of Uphill Condition

匀速上坡时候，忽略了迎风阻力和加速惯性阻力，只考虑上坡阻力，根据受力平衡，则：

对铰支点取矩：

对下铰接点取矩为0∑M1=0；对R5作用点取矩为零∑M2=0。由以上的方程可以求出阻力P1、P2、R1、R2、R4、R5。

3 后车架不同工况应力分析

3.1 有限单元模型

后车架由连接板、铰接板、后桥连接板、档板等结构组成，不但承受压力，还承受弯矩。选用壳单元建模模拟[9-10]。除与摆动架连接的前后轴承板用实体单元外，其余均用壳单元建立模型，实体单元与壳单元通过共同的节点连接。前后轴承板选用实体单元是为了更接近真实模型的刚度，因为前后轴承板的厚度过大，如果使用壳单元进行模拟，将与真实的刚度相差过大。

在与摆动架连接的圆形区域也是选用三角形单元进行了细划处理。后车架模型共有节点6073个。有限单元模型，如图6所示。车架选用的材料为16Mn，屈服极限[σ]s=345MPa，安全系数设计为n=1.2，则最大许用应力[σ]=287MPa。

图6 后车架模型Fig.6 Rear Frame Model

3.2 不同工况分析

3.2.1 满载匀速运行

满载匀速运行时，只需加载在后车架的相应受力位置，获得应力集中区域，如图7所示。

图7 应力集中区域Fig.7 Stress Concentration Area

从图中可知，整体受力情况比较均匀，受力不大。受力比较大的位置是后车架与摆动架连接的轴销作用位置和鹅颈部位，最大应力是101.6MPa，，在材料许可应力的范围内。

3.2.2 满载举升工况

满载举升的时候，主要的受力部位是与举升油缸和与货箱铰接处，应力分布云图，如图8所示。

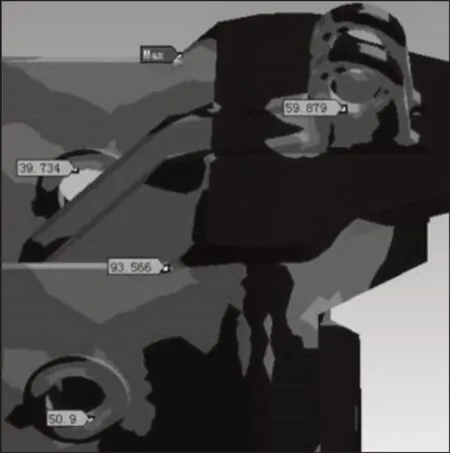
图8 应力分布云图Fig.8 Stress Distribution Nephogram

如图可知，满载进行举升操作时，开始进入举升流程时，系统的承载较大，最大变形和受力区域为鹅颈和高副支撑附近，变形和应力集中比较明显，最大应力值达到235.1MPa，满足材料的许可应用范围，同时铰接点连接区域变形较大，需要予以改进加强。

3.2.3 满载制动工况

车辆满载发生制动时，车辆应力最大位置与举升工况类似，位于高副支撑和车架尾部的铰接点。应力分布云图，如图9所示。由图可知，在此工况的最大应力为193.2MPa，满足材料的许可范围，鹅颈区域为应力集中区域，需进行改进设计。

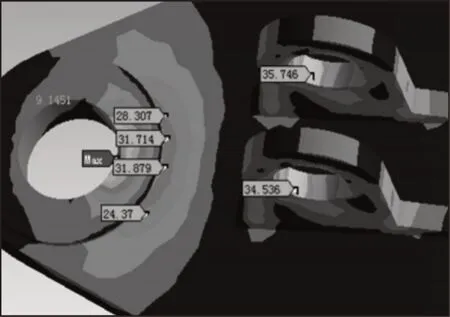
图9 应力分布云图Fig.9 Stress Distribution Nephogram

根据以上分析，获取不同工况的应力状态，如表1所示。

表1 各工况应力状态Tab.1 Stress State of Each Working Condition

由不同工况分析结果可知，车架的整体受力均匀，最大应力值均在许可的范围之内，当在鹅颈和铰接点处出现了应力集中，需对相应区域进行优化设计和改进。

3.3 方案优化设计

针对以上分析，从材料、结构和焊接工艺等方面进行改进：材料优化，针对鹅颈和铰接点处的材料进行优化增厚，其中，鹅颈处材料由原来55mm，变更为65mm，而在铰接点处增加30mm的支撑筋板；对应力集中处的圆角进行放大，原来的半径为10mm，放大到15mm；对焊缝的焊接工艺进行调整，增大焊接电流由10kA提升到10.6kA，提升焊接时间，由15ms增加到25ms，增加焊缝的厚度，由3mm提升至5mm，以此提升焊接质量。根据优化设计方案，对车架模型进行修改，进行重新计划，获取变化后应力分布，如图10所示。

图10 改进后应力分布Fig.10 Stress Distribution After Improvement

由图可知，通过改进设计以后，应力集中得到明显改善；获取满载举升工况下的最大应力降低到186.3MPa，得到明显改善，满足材料的许可范围。

4 实车测试分析

为验证有限元分析及改进方案的可靠性，选用应变片式应力测试系统对关键区域进行测试，主要实验设备及实验用车，如图11所示。根据前文分析在应力分布较大的位置黏贴应变片。

图11 测试系统Fig.11 Test System

根据以上分析结果，在鹅颈处和铰接点后侧加强板处布置传感器，获取满载举升工况时，最大应力的分布情况。

车辆从空载运行开始，进行测试，整个过程包括装载、运输、举升等，在整个过程中，应力波动变化，最大值分别与仿真值进行比较，如表2所示。

表2 测量点的最大值对比（MPa）Tab.2 Measurement Point Extreme Table（MPa）

分析结果可知，优化设计后，在满载举升工况，车架的应力分布得到明显改善，应力集中现象得到有效改善，同时测试与仿真结果对比可知，二者的误差控制在6%以内，均小于优化值，表明有限元分析的可靠性，同时验证了模型的准确与可靠性。

5 结论

（1）结构整体满足使用，但在满载举升工况，鹅颈处和铰接处存在应力集中和最大值分布，最大值为235.1 MPa，小于材料的需用应力，设计时需要重点关注；（2）针对应力集中和较大位置，采用厚度提升、圆角放大、优化焊接工艺等方案，可以有效改善应力集中现象，最大值具有明显降低；（3）采用应变片对实车进行测试，满载举升工况，最大值分别为195.48MPa、159.21MPa，测试结果与仿真值之间的误差小于6%，同时均小于优化前的数值，表明优化方案是可行的，优化设计方案和分析结果是可靠的。