单摆永磁直驱式波浪能发电装置的性能研究

李文宏，管 超，刘 晨

（山东科技大学海洋科学与工程学院，山东 青岛 266590）

1 引言

随着海洋开发范围从浅蓝到深蓝，由近海向远海的持续推进，海洋仪器的长期能源供应已然成为制约其发展的短板问题[1]。现阶段海洋仪器的供能方式多为蓄电池和太阳能，受工作环境的限制并不能持续稳定地为仪器供电。研究高转化效率的自然能量收集装置成为提高海洋仪器续航能力的有效手段。波浪能作为一种储存量大、分布面广的清洁可再生能源，是为海洋仪器提供能量的绝佳选择。实现海洋仪器的就地取能、能量自给功能，将提高其远距离、长时间、高稳定性的工作能力，对海洋资源开发利用、海洋环境监测、海洋灾害预警等方面具有重大意义。

为实现海洋传感器节点的自供电，国内外学者在能量收集和转换技术方面做了大量研究。文献[2]设计了一种电磁摩擦复合式波浪能量收集器，在工作频率为3Hz时，总功率密度为1.57W∕cm3；文献[3]利用压电技术提出了一种振动棒型波浪能收集器，平均输出电压为2.42V；文献[4]提出了一种与浮标结合的压电式波浪能发电装置，输出功率为53.7µW；文献[5]设计的海洋摆动发电系统在0.5Hz 的激励条件下，输出峰值电压为1.5V，最大输出功率0.7W；文献[6]利用AQWA 对一种球形波浪发电装置进行了运动性能研究。

整体来看，现阶段的波浪能量转换装置普遍存在输出功率低、装置本身与海洋仪器的体积匹配度差、环境适用性差等需进一步改善的问题，基于电磁感应定律，采用易于起振的摆式结构，设计了一种与小体积球形浮标相结合的单摆永磁式波浪能发电装置。选用永磁体作为磁动势的摆式发电装置，在低频率运动条件下，可以提供较高的磁能密度和能量转换效率。

2 系统的基本结构与发电原理

研究的单摆永磁式发电装置的物理模型示意图，如图1 所示。其结构主要由球形浮体外壳、摆杆、线圈绕组、线圈铁芯，永磁体、磁扼等部件构成。

图1 永磁式波浪发电装置结构示意图Fig.1 Schematic Diagram of Permanent Magnet Wave Energy Generation Device

当浮标体在波浪的冲击作用下发生摇荡运动，摆锤在装置内部与浮标体之间发生相对摇动，从而导致线圈绕组与永磁体之间发生相对运动，由电磁感应定律可知，当闭合的线圈绕组与永磁体之间发生相对运动时，线圈做切割磁感线的运动，而且线圈中的磁通量也会变化，从而产生感应电动势。

线圈中的感应电动势可用下式［7］表示：

式中：E—感应电场强度；Φ—线圈的总磁通；φ—每匝线圈的平均磁通；N—线圈的匝数。

这里设计的波浪能量转换装置具有以下优点：

（1）采用直驱式两级能量转换，减少了传统发电装置的传动蓄能机制，在减少能量损耗的同时提高了装置的可靠性；

（2）优化能量转换部分运动方式，改善与波浪低频运动特性的匹配度，从而提高了能量吸收与转换的效率；

（3）采用内置式结构，即发电部分位于能量俘获装置的内部，既能够满足发电部分与俘能部分的匹配度要求，又可避免与海水的直接接触，进一步提高装置的寿命与可靠性。

3 运动性能模拟

根据前文所介绍的系统发电机理可知，球形浮标体的摆动角度以及摆锤的相对摆动角度的大小是衡量系统吸收能量大小的主要依据。使用物理方程描述装置在波浪中的运动，并依靠AQWA软件对装置进行运动性能的模拟。选择波浪入射角度β=0°，分析波浪激励力随入射波频率的变化规律；讨论装置外部壳体的纵摇以及摆锤的相对纵摇运动响应的变化规律。

3.1 运动方程

为描述整个装置在波浪作用下的运动情况，引入整体的固定参考坐标系Oxyz，设原点O位于未扰动的海平面上，z轴垂直于海面向上；外部壳体的参考坐标系Ob-xyz原点位于重心Ob处，为随体坐标系，并假设该处为转动中心；摆锤参考坐标系Op-xyz原点位于摆锤重心Op处，摆长为l。

我们只取发电装置外部壳体的纵荡运动、垂荡运动、纵摇运动以及摆锤的相对纵摇运动为研究对象进行讨论，分别用Xp，Zp，α，θ表征上述四个自由度的运动，定义位移矢量如下：

浮标体的运动用其重心Ob的位移表示，摆锤的运动用其重心Op的位移表示，则有：

根据Lagrange方程可建立整个系统的运动方程：

式中：M—装置整体的质量矩阵；FH—波浪力；A—附加质量矩阵，与装置外壳的形状和加速度有关；Fg—重力作用矩阵；Fc—静水恢复力矩阵；FPTO—电磁阻尼矩阵。

通过进一步地简化可以得到，以相对摆动角度表征的多参数激励下的摆锤非线性运动方程[8]为：

3.2 入射波浪频率对浮标体所受波浪激励力的影响

浮标体在波浪作用下受到的激励力由两个部分组成：F-K力和绕射力。利用势函数对物体湿表面进行积分，得到浮标体所受波浪力[9]。其表达式为：

为讨论在给定波浪入射角度下各个运动模态的波浪激励力之间的关系，给出在波浪入射角度为0°时，浮标体在六种不同模态下波浪激励力的变化对比曲线，如图2所示。

图2 外部壳体不同模态下波浪激励力的变化曲线Fig.2 The Change Curve of Wave Force of Shell in Different Modes

从图中可以明显发现浮标体纵荡、垂荡、纵摇三种模态所受到的波浪力的大小明显高出于另外三种运动模态，也就说明，在入射波浪角度为0°时，浮标的主要运动形式即为纵荡、垂荡和纵摇，其他三种模态的运动响应并不明显。而摆锤与浮标体的相对纵摇角度是影响装置发电能力的主要因素，因此，在后文中我们将以摆锤的相对纵摇运动为对象，着重进行讨论。

3.3 入射波浪高度对摆锤相对纵摇运动的影响

在入射波角度β=0°，波浪周期T=3.5s，波高分别为0.2m、0.4m、0.6m、0.8m、1.0m、1.2m的波浪条件下，研究波浪高度对摆锤相对纵摇运动的影响，其仿真结果，如图3所示。

图3 不同波浪高度下摆锤相对纵摇响应曲线Fig.3 Relative Pitch Response Curve of Pendulum Under Different Wave Heights

由图3 可知，摆锤的相对纵摇响应曲线呈现为周期性的变化，波浪高度不断增加，响应幅值随之增加，波高为1.2m时，摆锤相对纵摇响应幅值的最值为41.25°。但明显可以看出，在波浪高度H=0.6m时，摆锤相对纵摇响应的变化曲线更稳定。

3.4 入射波浪周期对摆锤相对纵摇运动的影响

在入射波角度β=0°，波高H=0.6m，波浪周期分别为3s、3.5s、4s、4.5s、5s、5.5s的波浪条件下，研究波浪周期对摆锤相对纵摇运动的影响，其仿真结果，如图4所示。

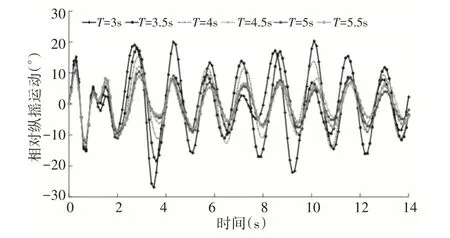
图4 不同波浪周期下摆锤相对纵摇响应曲线Fig.4 Relative Pitch Response Curve of Pendulum Under Different Wave Cycles

由图4可知，摆锤相对纵摇响应随着入射波浪周期的增加，运动趋势保持不变，但运动响应幅值减小。在波浪周期T=3s时，摆锤相对纵摇响应幅值的最值为20°，但相比较而言，在波浪周期T=4s时，摆锤相对纵摇响应的变化曲线最为稳定，而且运动幅值也较为理想。

综上，当波浪周期T=4s，波浪高度H=0.6m时，发电装置在保证运动稳定性的前提下，具有较理想的相对纵摇响应幅值。摆锤的相对纵摇运动周期约为2s，最大幅值约为21°，平均幅值为15°，因此选择摆锤在稳定状态下的运动响应与曲线θ=15sin（π·t）进行拟合对比，其结果，如图5所示。

图5 摆锤最佳相对纵摇运动曲线Fig.5 The Best Relative Pitch Motion Curve of the Pendulum

从图5中我们可以看到，两曲线间的吻合程度良好，完全满足拟合的基本要求。因此，综合仿真结果，有理由认为当波浪周期T=4s，波浪高度H=0.6m 时，摆锤的相对纵摇运动的运动状态为Tp=2s，最大幅值Ap=15°的振荡运动，暂不考虑相位问题，其运动可表示为：θ=15sin（π·t）。

4 发电性能模拟

所谓波浪能转换装置，其设计的根本出发点和最终目标都是实现电能的转换，本节使用在水动力模拟中得到的理想结果作为电磁仿真过程中的外部激励，建立发电模型并进行有限元仿真，讨论软磁材料的相对磁导率和气隙宽度对电磁转换的影响，最终求出线圈绕组的感应电动势以及输出功率。

4.1 静态仿真优化

4.1.1 软磁材料相对磁导率对磁感应强度的影响

软磁材料的磁导率决定了其导磁性能，导磁性能的强弱决定了穿过线圈的磁通量。磁通量与磁感应强度的关系可以表示为[10]：

式中：φ—单匝平均磁通；B—磁感应强度；s—线圈截面积。

在磁感应强度和铁芯尺寸一定的情况下，磁导率越大，磁饱和的数值越大，磁通量也就越大，线圈中的感应电动势也就相应提高。虽然装置选择的硅钢为非线性材料，其导磁性能由B-H曲线来定义，但通过定义相对磁导率常数的方法模拟其工作状态，对分析磁场的分布仍具有效性。在仿真中，设置铁芯相对磁导率μc的变化范围为（500～8000），其磁感应强度与相对磁导率之间的变化关系曲线，如图6所示。

图6 磁感应强度与相对磁导率的关系Fig.6 The Relationship Between Magnetic Induction Intensity and Permeability

从图中可以看到，随着铁芯材料相对磁导率的增加，铁芯轴向路径上的磁感应强度也随之增加，磁通量也以相同的趋势增大，当相对磁导率达到6000后，曲线的增长放缓。所以，单纯的增大材料的相对磁导率并不会实现磁通量的持续增长，而且材料的相对磁导率越大，制造的成本也会相应增加，结合仿真结果，选取相对磁导率为6000的硅钢作为装置的软磁材料。

4.1.2 气隙宽度对磁感应强度的影响

气隙是指线圈铁芯与永磁体之间的空气间隙，空气的磁导率远远低于软磁材料，因此在磁感线传递到气隙中时势必会引起扩散，使磁损耗增大的同时引起边缘效应，影响发电质量。在仿真中设置气隙宽度δ的变化范围为（2～15）mm，磁感应强度与气隙宽度之间的关系曲线，如图7所示。

图7 磁感应强度与气隙宽度的关系Fig.7 The Relationship Between Magnetic Induction Intensity and Air Gap

由于磁感应强度和磁通量具有相同的变化趋势，因此在这里只给出了磁场强度的变化曲线。从图中可以看到，当气隙宽度逐渐增大时，铁芯中的磁感应强度呈现出近乎直线的下降趋势，这样的变化趋势说明，磁感应强度的大小受气隙宽度的影响十分明显，气隙宽度越大，漏磁越多，磁感应强度越小，磁通量也就越小，发电效率也就越低。因此，在设计的过程中应该使得气隙宽度尽可能小，来减少漏磁现象的发生，但考虑实际加工与安装，选择最终的气隙宽度为2mm。

4.2 动态仿真

假设浮标保持静止，摆锤部分做相对摇动，利用动态仿真进行结构优化，动态仿真初始参数，如表1所示。

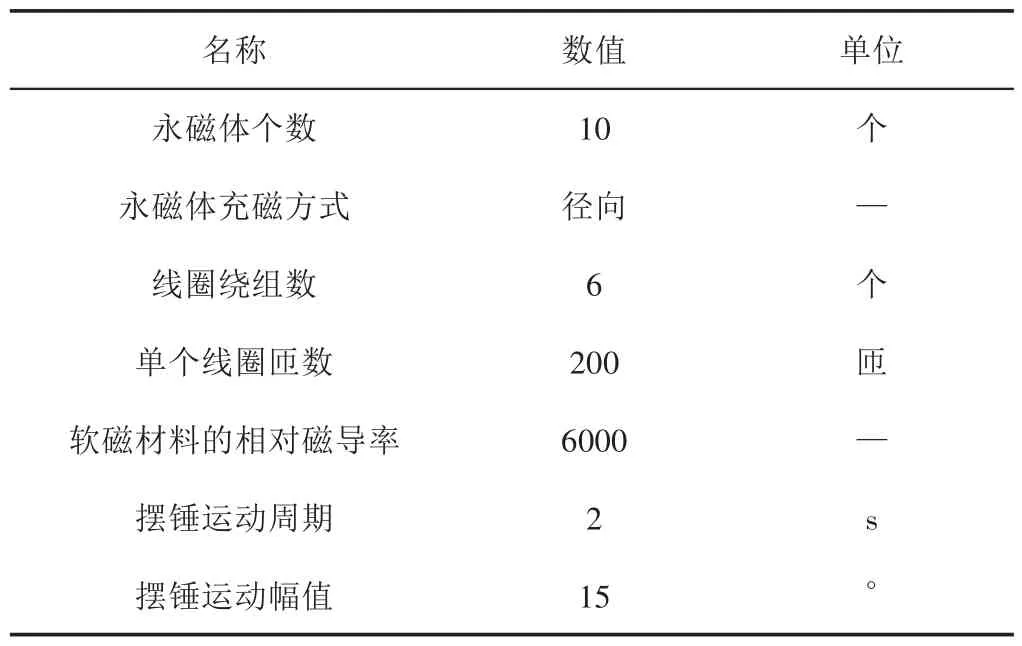
表1 Maxwell动态仿真初始参数表Tab.1 Maxwell Dynamic Simulation Initial Parameter Table

我们将摆锤的运动近似为周期Tp=2s，最大幅值Ap=15°的往复振荡运动，并将6匝线圈定义为独立的6相绕组，每相的匝数N=200。经仿真得到的线圈磁链和空载电动势，如图8、图9所示。对比图8和图9中可以看出，单相绕组上的磁链与产生的感应电动势呈现对应的周期性变化，变化周期为1s，最大磁通为1.92Wb，最大感应电动势为10.57V。

图8 六相绕组的磁链变化Fig.8 The Flux Linkage Change of Six-Phase Winding

图9 六相绕组的感应电动势变化Fig.9 The Induced Electromotive Force Change of Six-Phase Winding

同时，从图9中可以看出A相、C相和E相同相，B相、D相和F相同相，因此我们考虑采用同极串联的思想，将A相、C相和E相合为一相Phase_A，将B相、D相和F相合为一相Phase_B，这样不仅可以提高单相绕组内产生的感应电动势，还有利于后期的电能处理。合并后的磁链和感应电动势波形，如图10、图11所示。

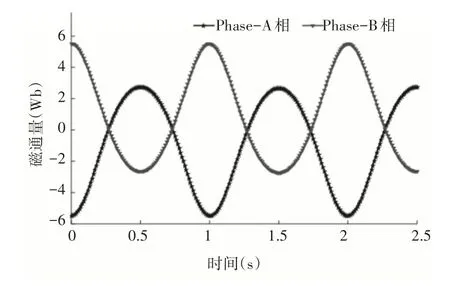
图10 绕组结构优化后的磁链变化Fig.10 The Flux Linkage Change After Winding Structure Optimization

图11 绕组结构优化后的感应电动势变化Fig.11 The Induced Electromotive Force Change After Winding Structure Optimization

从图10、图11中可以看出，两相绕组中的磁链与产生的感应电动势均为相互对应的周期性变化，与优化前相比，周期未发生改变，其中Phase_A相磁通量最大值为-5.49Wb，感应电动势最大值为27.7V，Phase_B相磁通量最大值为5.49Wb，感应电动势的最大值为27.7V。

由此可知，Phase_A和Phase_B两相所产生的感应电动势幅值大小相等，相位相反。与线圈结构优化前相比，单相输出空载电动势的能力提高了2.6 倍，在未对电能造成明显损失的情况下提高了单项绕组的输出能力，对后期的电能处理与应用具有重要意义。

在低频条件下，线圈内的感抗与阻抗相比可以忽略不计。线圈内阻可表示为：

式中：ρc—铜的电阻率；

Lc—漆包线的长度；

Ac—漆包线的横截面积。

选用直径dc=0.8mm的漆包线，其电阻率ρc=34.8Ω∕km，从而可以求得单相线圈内阻Rc=46.2Ω。易知，当外接电阻与线圈绕组的内阻大小相同，即R0=Rc时，装置可达到最佳输出功率，其表达式为：

式中：U—单相总感应电动势；

R0—外接负载电阻；

Rc—线圈绕组的内阻。

所以将电阻值代入式（9），在理论上可以求得单相的最佳输出功率为P0=2.07W。

5 结论

利用永磁材料的电磁特性，选择易于起振的摆式结构，提出一种与小型球形浮标相结合的单摆永磁式波浪发电装置，推导了在波浪激励下的运动模型，使用AQWA与Maxwell进行了联合仿真，分析了其运动规律与发电性能。主要结论如下：

（1）当波浪入射角度β=0°，装置外壳的主要运动形式为纵荡、垂荡和纵摇，摆锤的相对纵摇运动幅值与波浪高度成正比，与波浪周期成反比；在波浪周期T=3.5s，波浪高度H=0.6m的波况下摆锤做较为理想的周期Tp=2s，幅值Ap=15°的往复振荡运动。

（2）通过优化发电装置线圈结构可有效提高感应电动势，在f=0.5Hz 的摆动频率下，单相绕组产生的最大感应电动势U0=27.7V，最佳输出功率P0=2.07W。与前文中提到的发电装置相比，虽结构尺寸与发电原理不尽相同，但输出的电动势与功率具有较明显的提升，可以有效满足各类海洋仪器与无线传感器节点的供电需求，具有广阔的应用前景。