直流电压下局部放电数值模拟方法研究综述

2024-04-27陈芳，荣娜，胡晓，2，3

绝缘材料 2024年4期

陈芳，荣娜，胡晓，2，3

（1. 贵州大学电气工程学院，贵州贵阳 550025；2. 浙江大学电气工程学院，浙江杭州 310027；3. 浙江天际互感器股份有限公司，浙江衢州 324100）

0 引言

随着新型电力系统的发展，直流输电技术广泛应用于大规模清洁能源超远距离、跨区域、大容量传输等领域，同时也对直流电压下电气设备绝缘系统的设计和故障诊断提出了新的挑战[1-2]。

绝缘材料在制造、运输、安装及运行过程中不可避免地会出现绝缘缺陷[3]。在这些缺陷处，电场会发生畸变，进而容易引起局部放电，放电持续发展会使绝缘性能恶化，甚至导致绝缘失效[4]。直流电压下的局部放电特性与交流电压下的显著不同，首先，交流电压下的电场分布由绝缘介电常数决定，而稳定直流电压下的电场分布取决于绝缘电导率；其次，由于在稳定直流电压下电压幅值和极性保持不变，缺陷处电场的变化主要受局部放电产生的空间电荷影响，这使得下一次局部放电的发生和终止取决于空间电荷的衰减和积累。因此现有的交流电压下局部放电的机理、检测和分析方法并不完全适用于直流电压下局部放电的研究。目前对直流电压下局部放电现象的认识和分析仍处于研究阶段，尚未有专门针对直流电压下局部放电检测和评估的国际标准[5]。为了更好地了解直流电压下局部放电的机理和特性，有必要对其发展过程进行深入研究。

本文首先介绍了直流电压下局部放电的机理，在此基础上进一步介绍了直流电压下局部放电数值模拟方法的3种模型，即三电容模型、电导模型和等离子体模型，其中重点介绍了各模型的建模方法，总结各模型的优缺点，并对国内外学者采用这些模型对直流电压下局部放电的研究进行了梳理。最后分析了温度、绝缘材料、电压谐波、大气压、绝缘缺陷等因素对直流电压下局部放电的影响。本文旨在归纳总结直流电压下局部放电数值模拟方法的研究现状，为后续直流电压下局部放电仿真的相关研究提供参考。

1 直流电压下局部放电的物理模型

1.1 直流电压下局部放电的机理

局部放电的发生需满足两个条件：电场超过临界值和生成自由电子[6]。在电压作用下，当绝缘气隙上施加的电场大于该气隙的临界电场且有自由电子生成时，气隙中就会发生放电，放电生成的正、负电荷在外电场作用下沿相反方向运动，积聚在气隙两端并形成与外加电场相反的电场，使得气隙内停止放电[7]。经过一定时间后，聚集在气隙表面的电荷发生复合而衰减，导致气隙内的电场恢复至临界值，才可能出现第2 次局部放电，如图1 所示。与交流电压不同的是，直流电压下绝缘介质中的电场分布不再由介电常数控制，而是由介质的体积电导率和表面电导率决定，因此交流电压与直流电压下的放电机制有所不同[8]。气隙内发生放电的电场Εcav如式（1）所示。

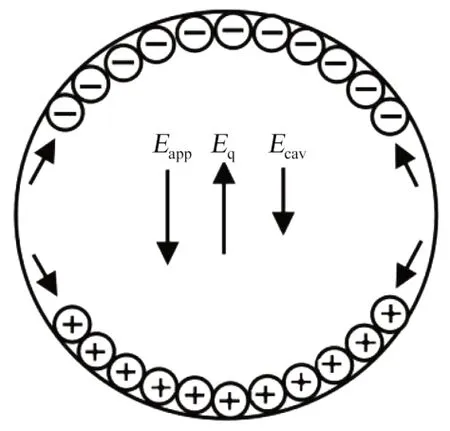
图1 气隙电场和表面电导率变化导致的电荷移动Fig.1 Charge movement due to changes of air gap electric field and surface conductivity

式（1）中：Εapp指施加电压时气隙内产生的电场；Εq指气隙表面电荷移动时引起的电场。

直流电压下，施加的电压幅值和极性保持恒定，导致气隙内Εcav和Εq方向始终保持一致，因此气隙表面电荷的衰减是气隙内发生放电后的熄灭电场恢复至临界电场以触发下一次放电的唯一条件。

随着计算机技术的发展，关于局部放电的数值模拟方法已成为继局部放电理论分析、实验分析后的又一科学研究方法[9]。通过建立局部放电的仿真模型，可深入了解绝缘缺陷从初始状态发展到老化甚至到击穿的过程[10]，有利于探究温度、电压幅值等因素与局部放电特性之间的关系[11]。此外局部放电的数值模拟方法不仅促进了局部放电机理的深入探讨，也推动了绝缘故障诊断技术的发展[12]。通过国内外学者对直流电压下局部放电数值模拟方法的研究，了解到目前其放电模型可分为三电容模型、电导模型和等离子体模型，3 种模型的优缺点如表1所示。

表1 3种物理模型的优缺点比较Tab.1 Comparison on advantages and disadvantages of three physical models

1.2 三电容模型

为模拟直流电压下缺陷的局部放电特性，U FROMM 等[13]在交流电压三电容等效电路的基础上，在3个电容处分别并联一个电阻，得到了直流电压下局部放电的三电容等效模型，如图2所示。图2中的Cc和Rc分别表示绝缘电介质顶部和底部之间的电容和阻抗；Cb和Rb分别表示气隙和电极之间串联的电容和阻抗；Ca和Ra分别表示气隙的电容和阻抗。

图2 直流电压下局部放电的三电容等效模型Fig.2 Three capacitance equivalent model of partial discharge at DC voltage

当气隙两端的电压（Ucav）超过局部放电的起始电压（Uinc）并有有效电子生成时，气隙会发生局部放电。放电结束后气隙两端的电压降低到放电的熄灭电压（Uext），当气隙两端持续加压并满足放电条件时将重复上述放电过程。图3为发生局部放电时气隙两端电压的变化。图3 中的tL表示达到初始电压后有效电子生成的时间，tR表示放电后从熄灭电压恢复到起始电压的时间。为了评估直流电压下的局部放电活性，除了要考虑局部放电的电荷量（内部和外部电荷）之外，还应考虑两个连续放电脉冲之间的时间间隔，J C DEVINS[14]和U FROMM[15]对其进行了理论分析。

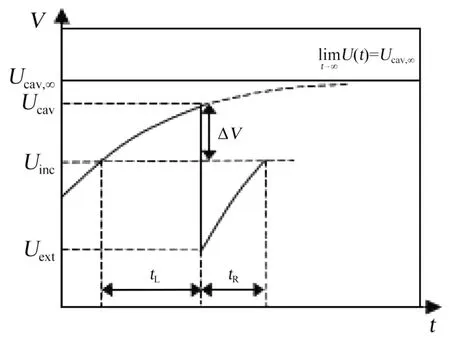
图3 发生局部放电时气隙两端电压的变化Fig.3 Changes of voltage at both end of air gap during partial discharge

由电路原理可知，气隙充电时间常数（τ）的计算公式如式（2）所示。

气隙两端的电压（Ucav）的计算公式如式（3）所示。

式（3）中，Ucav,∞为不发生局部放电时气隙两端电压的稳态值。

在直流电压下，因介质的电阻率有限，在发生一次局部放电之后，下一次的局部放电可能在某一时间间隔之后发生。在局部放电产生的过程中，自由电子生成的随机性导致电场在到达临界值之后并不会立即放电，即从电场超过临界值的时刻到放电发生的时刻之间存在一个时间延迟，称为放电时延。两次放电脉冲之间的时间间隔Δt指放电的恢复时间和放电时延之和[16]，如式（4）所示。

当Ucav,∞＞＞Uext且tL忽略不计时，Δt=-τln[1-(Uinc-Uext)/Ucav,∞]，取泰勒展开，取第1项得到式（5）。

则直流电压下的放电重复率（n）可以表示为式（6）。

从式（6）可知，直流电压下的放电重复率与Ucav,∞呈正比[17]。与交流电压下局部放电相比，相同幅值的直流电压下放电重复率要低几个数量级，但其单次局部放电的电荷量、放电波形、放电形状等与交流放电下的相同[18]，直流电压下局部放电的视在电荷（qapp）和实际放电量（qreal）[6]可分别表示为式（7）、式（8）。

因直流电压没有交流电压工频相位的概念，直流局部放电通常以放电幅值q、时间t（或两次放电脉冲之间的时间间隔Δt）及规定时间内的放电次数N之间的关系建立q-t、q-N、N-t图来展开分析[19]。P H F MORSHUIS 等[20]将三电容模型应用于高压直流设备中，研究了不同缺陷类型的放电特征，提出了直流电压下局部放电分类的不同方法，并用q-t图分别表示了气隙放电、油中杂质放电、表面放电以及电晕放电4种缺陷类型的放电现象。

曹馨予等[21]采用三电容模型研究了直流电压叠加交流电压时对绝缘间隙的局部放电幅值和放电重复率的影响。结果表明，与没有叠加交流电压的直流电压相比，当叠加的交流电压幅值小于局部放电的熄灭电压时，其放电幅值增加，但放电重复率远低于交流电压频率。N MORETTE 等[22]基于三电容模型探讨了电荷衰减时间常数（τ1）与缺陷几何电气参数（ρc）之间的关系，并搭建实验平台验证了电荷衰减时间常数随缺陷尺寸变化的理论与实验结果具有一致性。但在探讨τ1与ρc之间的关系时，因实验测量过程中缺陷内表面电荷复合及测量电路的频率响应等因素影响，导致实验结果与理论值存在一定的偏差。

LI Y 等[23]采用三电容模型分析了直流电压下油-纸绝缘系统中放电重复率与温度的关系，根据模型中的方程组分析得到，温度影响介质的电阻率，从而影响气隙的放电行为，随着温度升高，放电重复率将增大一个数量级。例如，在室温下每分钟的放电重复率为8～12次，当温度升高到40℃时，放电重复率仅观察到每分钟1～10 次，之后随着温度持续升高，放电重复率呈指数递增。O ZIDANE等[24]采用三电容模型分别研究了在直流电压、交流纹波电压下不同气隙尺寸和温度对交联聚乙烯绝缘材料含圆柱形缺陷时局部放电行为的影响。结果表明直流电压、交流纹波电压下的最大放电幅值均随温度的升高而增大，但两者的放电重复率不同，直流电压下的放电重复率随温度的升高而增大，而交流纹波电压下的放电重复率随温度的升高而减小。其原因在于交流纹波电压下的放电重复率只受初始电压的影响，而直流电压下的放电重复率则受时间常数的影响。此外，该研究中的放电幅值与气隙高度呈正相关，而放电重复率随着气隙高度的增加而减小。

三电容模型将局部放电过程简化为求解局部放电的放电时间间隔和电容的充放电过程，便于考虑放电的发生和放电量的计算，在局部放电仿真研究中已得到众多应用。但直流电压具有恒定的电压幅值和极性，缺陷内电压的变化取决于空间电荷的移动以及缺陷表面电荷的积累和消散。而该模型中并没有具体描述与缺陷内局部放电有关的电荷复合、累积、消散的过程，且模型中只有当缺陷表面为等电位时，定义的电容才有效[25]，故不能准确地反映气隙内电压的变化，进而无法区分局部放电的位置。

1.3 电导模型

气隙放电可通过放电时改变气体的电导率来模拟，C FORSSEN 等[26]据此提出了基于有限元分析的局部放电仿真模型，用于动态计算气隙放电的脉冲序列，后有学者将其应用于研究直流电压下的局部放电特性[8]。

介质和气隙两端的电场分布遵循高斯定律、欧姆定律及电流连续性方程[18]，如式（9）～（11）所示。

式（9）～（11）中：D为电位移，C/m2；J为电流密度，A/m2；ρ为自由电荷的体密度，C/m3；σ为电导率，S/m；Ε为电场强度，V/m；t为时间，s。

将式（9）～（11）相结合可得到电场控制方程，如式（12）所示。

式（12）中，V为电势差，V。

运用计算机软件，代入各数值求解公式（12），可得到电导模型的电势和电场分布。图4为电导模型的常用结构图，其中1 为气隙缺陷；2 为气隙表面（将气隙表面建模为薄层，可用于模拟沿气隙表面传导导致的电荷衰减）；3 为绝缘材料；上电极接高压电源，下电极接地，侧边边界为电绝缘，所有的内部边界采用了连续性条件。

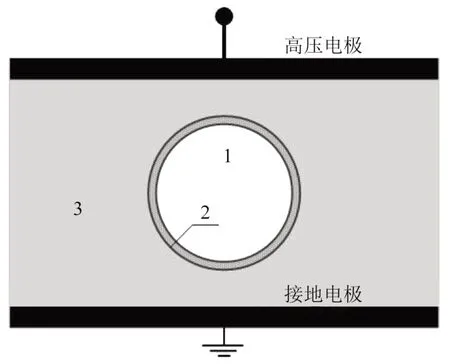
图4 直流电压下的电导模型Fig.4 Conductivity model under DC voltage

根据直流电压下局部放电的原理，其产生的条件之一是要有满足超过临界值的电压。结合气体击穿理论中的汤姆逊机理和巴申定律，可得到介质击穿的临界场强Εinc的表达式[27]如式（13）所示。

式（13）中：(Ε/p)cr、n和Β是与气体电离过程相关的系数；p为气隙压强，Pa。对于空气而言，n=0.5，Β=8.6 Pa0.5·m0.5，(Ε/p)cr=24.2 V/(Pa·m)，则临界电压Uinc的计算如式（14）所示。

式（14）中：ρ0为P=1.013×105Pa和T=293 K时的空气密度，kg/m3；d为平行于施加电场的气隙高度，m。

自由电子的生成也是发生局部放电的条件之一，体积电离和表面发射是自由电子生成的主要机制[27]。其中体积电离与气体辐射电离以及电子、负离子的场分离有关，考虑到体积电离很难发生，建模中通常将其设置为一个常数。表面发射主要通过离子碰撞、电极发射及表面光辐射释放电子，其满足Richardson-Schottky 规律[28]，表达式如式（15）所示。

式（15）中：Nes为表面发射的电子生成率，s-1；Ne0为初始电子生成率，s-1；Ne0=ζ(q/e)，其中ζ为比例系数，指电子能从载流子中脱离出来的比例，与表面电荷极性有关，q为电荷量，e为基本电荷量；tPD为距离上一次放电发生的时间，s；τ1为时间常数；ν0为基本声子频率，Hz；kb为玻尔兹曼常数，eV/K；T为热力学温度，K；Φ为有效逸出功，eV；ε0为真空介电常数。运用MATLAB 中的随机数生成器对初始电子的生成进行建模，得到局部放电发生的概率P，如式（16）所示[29]。

式（16）中，Net为总自由电子的生成率，s-1，Net=Nes+Nev，其中Nev为体积电离的电子生成率，s-1。当气隙两端的电压Ucav超过放电的起始电压Uinc且有P大于随机数R（0＜R＜1）时，局部放电发生。文献[11,30-36]在放电发展期间通过改变气隙电导率来模拟沿放电通道的放电电流，各文献气隙内电导率的取值如表2所示。

表2 气隙内电导率的取值Tab.2 The value of electrical conductivity in the cavity

表2 中：σcavmax为放电期间气隙内的最大电导率；Ucav和I分别为穿过气隙的电压和电流；Icirt为电子雪崩的临界电流；σcav0为气隙内的初始电导率。表2中第2行和第4行的最大电导率σcavmax是介于1×10-4～1×10-2S/m 之间的常数[30]。文献[7]给出了计算局部放电活动期间气隙最大电导率的表达式，如式（17）所示。

式（17）中：e为电子电荷；me为电子质量；λe为电子的自由行程；ce为电子热运动的速率；ne为电子密度。

直流电压下，电场的分布与电导率有关，而电导率取决于电场和温度[37]，如式（18）所示。

式（18）中：Α为电流密度常数，A/m2；Β为电场相关的常数，m/V；φ为热活化能，eV；q1为基本电荷量，C；Ε为电场强度，V/m。

在发生局部放电期间，随着电导率的增加，气隙内的电场低于放电的熄灭电压Uext时，放电终止，气隙的电导率恢复到初始值。运用欧姆定律对发生放电所得的电流密度进行积分，可计算每个放电脉冲的电荷量[38]，如式（19）所示。

式（19）中，S和Δt1分别为放电区域的横截面积和放电脉冲的持续时间。

A SAHU 等[39]建立了电导模型研究XLPE 绝缘样品中人工气隙缺陷的放电，通过改变气隙几何形状、气隙位置及直流电压幅值，计算气隙内的电势、电场及放电活动的分布。研究表明，气隙内的最大电场取决于气隙的大小、形状和位置。放电过程中，由于绝缘介电常数和气隙表面上的电荷积累，电场在气隙和XLPE 交界处发生畸变。与球型相比，椭圆形气隙表面边界附近的电场畸变更大。M SAGHAFI 等[40]运用电导模型研究了直流电压下的局部放电特性，并对内部有无气隙的聚乳酸（PLA）样品进行对比实验。结果表明，在直流电压下，内部有气隙的样品会出现局部放电，当直流电压为3.45 kV时，平均放电时间间隔为10 ms，且放电量和放电重复率的实测值与模拟值之间具有良好的一致性。

GU X 等[41]通过建立电导模型研究了不同外加电压和温度下XLPE 夹层中存在气隙时的局部放电特性，并考虑到XLPE的电导率与场强和温度有关，计算了气隙内的电场分布。结果表明，在研究70℃和30 kV稳定电压下的局部放电时，若不考虑XLPE电导率与温度的关系，气隙内电压的计算误差约为500%，且随着温度升高，电场畸变加剧。不同温度和直流电压下的放电重复率如图5 所示，在施加相同电压下，当温度从23℃升高到70℃时，放电重复率增加了2 个数量级，与实验结果一致。赵洋等[42]运用电导模型研究±320 kV 电缆预制式终端复合界面上气隙缺陷的放电，并建立温度和气隙位置等随机因素条件下电缆接头的局部放电概率密度函数，以研究直流试验电压幅值与电缆预制式终端气隙缺陷检出率之间的关系。结果表明，气隙缺陷检出率与环境温度、直流试验电压的函数关系式符合4次方幂函数关系式，当直流试验电压取1.85U0、温度取20℃时，气隙缺陷的检出率为99.25%，而温度取30℃时，气隙检出率可达99.85%，即检出率随着温度的升高而升高。

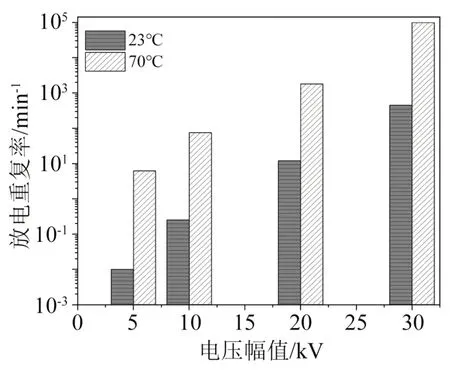
图5 23℃和70℃时直流电压下的放电重复率Fig.5 Discharge repetition rate under DC voltage at 23℃ and 70℃

LU Y 等[43]考虑交联聚乙烯电缆在直流电压下的场强分布主要与电导率有关，运用电导模型研究了交、直流电压下320 kV 直流电缆接头存在不同缺陷类型时的电场分布和放电起始电压。研究表明，气隙缺陷中的电场畸变最小，其直流电压下的初始放电电压是交流电压下的1.2 倍；凹陷缺陷在直流电压下的初始放电电压是交流电压下的1.09 倍；划痕缺陷在直流电压下的放电起始电压是交流电压下的1.075 倍；断痕缺陷在直流电压下的放电起始电压是交流电压下的1.05 倍。此外，研究指出因电缆缺陷类型和尺寸的多样性，相关研究需要进一步改进。

综上，与三电容模型相比，电导模型具有更为广泛的适用性，可以连续模拟局部放电过程，实时计算放电电流、感应电荷以及电压等变量，并准确反映实际放电电荷的分布以及多物理条件下的放电现象[8]，其仿真结果与实际情况相符，适用于多次、大量局部放电的仿真分析以及统计局部放电特性与发展规律的研究。

1.4 等离子体模型

传统的三电容模型通过引入放电恢复时间和放电时延来解释直流电压下绝缘气隙的局部放电特性，其中放电恢复时间采用电容的充放电原理计算。事实上，稳定直流电压下气隙电场的变化取决于电荷的运输，放电恢复时间取决于表面电荷的衰减。当放电发生后，残余电荷在外加电场的作用下在气隙表面积聚[44]，使得气隙内电场减小，甚至导致放电终止。在放电间隔期间，表面电荷的衰减使气隙的电场恢复至临界值，随着自由电子的生成，在满足放电条件后又将发生下一次放电，因此放电恢复时间实际上取决于表面电荷的衰减。大多数研究人员都已意识到这一点[14,17]，但因缺乏对放电期间表面电荷分布的了解，导致对直流电压下局部放电的研究尚未考虑表面电荷的衰减。在之前的研究中，有学者发现表面电荷衰减时间为1 s[45]。由于该衰减速度非常快，传统测量技术（如静电探针）很难测量到表面电荷的衰减[46-48]。此外，表面电荷的累积由单次局部放电过程中生成的电子、正离子和负离子的移动而产生。因此，为了更好地理解表面电荷衰减对局部放电特性的影响，应定量描述由电荷经碰撞电离、漂移、扩散和中和等组成的放电过程。等离子体模型最初用于模拟电极间的气体放电[49]和介质阻挡放电[50]，由于其工作原理与局部放电有着一定的相似性，R BARTNIKAS等[51-52]使用等离子体模型模拟单个局部放电的过程，并采用流体方程模拟局部放电的发展过程，同时考虑电离过程、电荷漂移、扩散、复合[53]、等离子化学反应及边界条件[53]，得到该模型定量描述局部放电发展的方程如式（20）～（22）[54-55]所示。

式（20）～（22）中：Ne、Np、Nn分别为电子、正离子和负离子的空间电荷浓度；t为时间；α、η、β分别为碰撞电离系数、附着系数和复合系数；We、Wp、Wn分别为电子、正离子和负离子的迁移速度；De为电子扩散系数。为减少计算时间，忽略二次放电过程。

当电荷到达气隙表面时，电子、正离子和负离子的迁移速度为0，此时表面电荷密度Ns的计算如式（23）所示。

式（23）中，ΔS和ΔV分别指单位面积和体积。局部放电生成的电荷对电场的影响不容忽视，因此采用泊松方程计算气隙内的电势分布，表达式如式（24）所示。

式（24）中：V为电势；εr为介质相对介电常数。在边界处采用泊松方程表示，如式（25）～（26）所示。

式（25）～（26）中：dg为气隙的高度；Εz()和Εz()分别为上表面两侧电场在z轴的分量；Εz(0-)和Εz(0+)分别为下表面两侧电场在z轴的分量；Nsu和Nsd分别为上表面和下表面的电荷密度。上电极接正极性的高电压，而下电极接地。其中正离子或负离子迁移速度的时间步长计算如式（27）所示。

式（27）中：Δte,p为电荷迁移的时间步长；Δz为沿z轴的栅格长度；|We,p|max为电荷迁移速度的最大值。放电发生后，计算放电电流[47]，其计算公式如式（28）所示。

式（28）中：U为施加的电压；Ε为施加的电场；V为放电体积。放电时延服从指数分布[33]，表达式如式（29）所示。

式（29）中：P（0≤P≤1）为放电的概率；λ为指数分布参数。当放电发生后，表面电荷的衰减决定电场的恢复，表面电荷衰减率如式（30）～（31）所示。

式（30）～（31）中，σp0、σe0分别为介质表面的初始正电荷和电子的密度。

为避免气体放电的汤森阶段，将一定浓度的自由电子放置在阴极附近，在外加电场的作用下，高浓度的电子促使放电过程直接达到流注阶段[56]。通过求解泊松方程，获得放电过程中气隙内的电荷和电场分布。因电子的迁移速度远高于离子的迁移速度，故分两步计算气隙内的电子和离子浓度。首先根据电子的迁移速度计算时间步长，并求解流体方程，当电子在界面处完全积累或被金属电极吸收后，开始计算气隙内的离子浓度。同理，根据离子迁移速度计算时间步长，并求解流体方程，当气隙内没有剩余电荷时，放电结束，如图6所示。

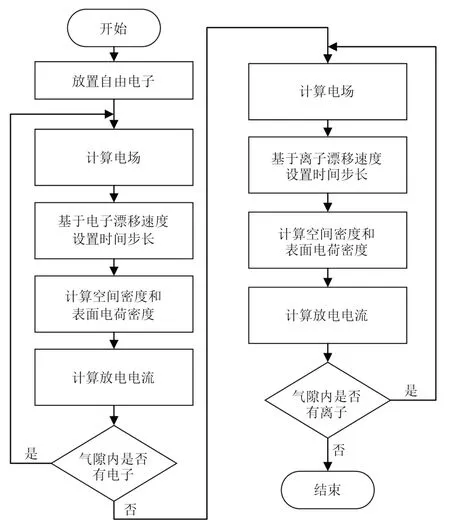
图6 单个局部放电模拟流程图Fig.6 Flowchart for the simulation procedure of a single PD

PAN C等[57]采用等离子体模型研究了直流电压下局部放电过程中表面电荷的动态分布。研究表明，正电荷的衰减速率高于负电荷的衰减速率，且局部放电会因表面残留电荷而再次发生。通过对表面电荷衰减的实验测量，得到正电荷的衰减时间约为573 ms，负电荷的衰减时间约为1 222 ms。此外，PAN C 等[58]采用等离子体模型探究了直流电压下局部放电的物理过程，研究表明，在局部放电的过程中，前一次放电产生的表面电荷衰减被认为是导致下一次放电发生的关键因素，且当对模型上电极施加正电压时，正离子和电子分别积聚在气隙下表面和上表面。因电子的迁移速度高于正离子的迁移速度，正离子的积累时间（约90 ns）比电子的积累时间（＜1 ns）长。同时，PAN C 等[58]为探究表面电荷衰减和放电时滞对局部放电的影响，计算了不同电荷速率参数下的放电结果，结果如表3 所示。从表3 可以看出，当指数分布参数λ保持不变时，放电时间间隔随着表面电荷衰减速率增加而减小；当指数分布参数λ增大时，放电时滞减少，放电时间间隔也相应减小。若放电时滞增加，表面电荷衰减时间变长，将导致表面残余电荷减少，从而降低对后续放电的影响。

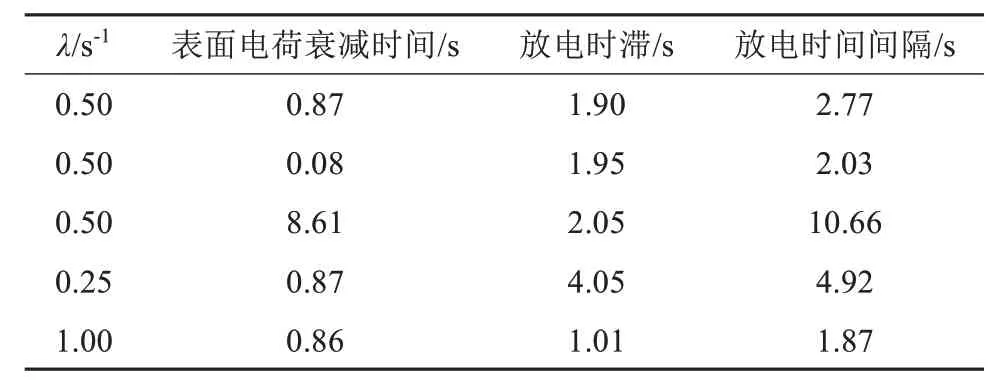
表3 不同电荷速率参数下放电结果的平均值Tab.3 Average values of discharge results under different charge rate parameters

综上，与其他模型相比，等离子体模型可以更为详细地描述单个局部放电的物理过程，进而促进局部放电发展的深入研究。但该模型所考虑的电子二次发射[59]和光电离[60]过程也为建模增加了计算量，因此等离子体模型只适用于少量局部放电的模拟分析，而不适用于需要大量数据的局部放电规律统计。

2 影响直流电压下局部放电的主要因素

国内外众多学者针对直流电压下的局部放电特性开展了大量的研究工作，系统分析了多个因素对局部放电特性的影响，如温度、绝缘材料、谐波、大气压、缺陷类型，并取得了显著的成果。

2.1 温度和绝缘材料的影响

直流电压下电导率是影响局部放电剧烈程度的重要因素，而电导率又受到电场分布和温度的影响。

E ILDSTAD 等[61]研究了聚丙烯绝缘层含气隙缺陷时温度对局部放电特性的影响。研究表明，在施加直流电压期间，放电频率与流经绝缘层的电流成正比，即放电的强度随温度和施加电压的增大而增大，放电频率、绝缘电导率与温度的关系如图7所示。BAO L W 等[62]研究了温度对脉冲直流电压下油-纸绝缘气隙内局部放电行为的影响。结果表明，随着温度的升高，放电脉冲序列倾向于出现在电压波形的正半周且逐渐减少，在负半周甚至已经消失。CHEN L 等[63]采用电导模型研究了电导率所引起的电场畸变对直流电压下局部放电的影响，并在室温和70℃下对试验样品进行了直流放电测试。结果表明，升高温度可以显著提升气隙内的场强，室温下的初始放电电压高于70℃时的初始放电电压，且仿真结果与实验结果一致。潘祖欣等[64]同样采用电导模型研究了温度对高压直流电缆中绝缘气隙内局部放电的影响，结果表明，放电重复率和平均放电电荷量随温度的升高而增大。

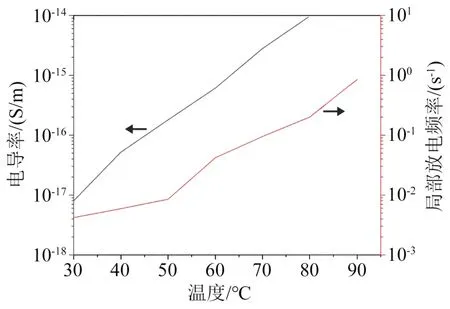
图7 放电重复率、绝缘电导率与温度的关系Fig.7 Relationship between partial discharge frequency,conductivity and temperature

M FLORKOWSKI[65]应用改进的三电容模型，分析了局部放电的起始条件和放电后的时间间隔，通过设计均匀的绝缘纸（PK）、XLPE、XLPE-PKXLPE、PK-XLPE-PK 4 种试样组合，证明了不同绝缘材料电导率会对局部放电活动产生不同的影响。由于XLPE 的电阻率高于PK 的电阻率，XLPE 试样连续放电脉冲之间的平均时间间隔最长。同时，研究还表明，绝缘材料电阻率与气隙电阻率之间的相互作用对于直流电压下局部放电的合理建模和模拟至关重要。T SHAHSAVARIAN 等[66]研究了乙烯-四氟乙烯（ETFE）和聚醚醚酮（PEEK）在斜坡电压、直流电压和不同温度下的表面放电行为。研究发现，尽管两种材料都表现出与其电导率有关的非线性放电行为，但ETFE 在100℃以上的高温下表现出更高的放电水平，为在高温条件下选择可抑制局部放电的绝缘材料奠定了基础。

2.2 电压谐波的影响

在电力系统整流转换过程中整流装置产生的谐波电压是不可避免的，谐波的注入可能影响电力设备绝缘系统的完整性，并加速绝缘材料老化[67]。M A FARD 等[38,68]研究了高压直流叠加电压谐波时对局部放电的影响，对聚合物绝缘板中的单个气隙进行建模，并运用MATLAB 和COMSOL 的交互环境进行仿真分析。研究表明，放电重复率与谐波振幅之间存在正比例关系，即随着谐波相对幅度的增加，放电脉冲数增加，且大多数放电脉冲出现在谐波电压的峰值处。此外，实验结果与仿真结果具有一致性。

LI Z L等[69]研究了频率为50～350 Hz的谐波分量叠加直流电压对高温超导直流电缆绝缘系统内局部放电的影响。结果表明，当叠加电压幅值保持一致时，放电幅值和放电重复率随谐波幅值的增加而增大。而谐波阶次的增加导致施加电压的时间导数沿相位变化，进一步促进了放电重复率的增大。芦山等[70]采用电导模型研究了电压谐波对高压直流电缆局部放电的影响，并搭建了检测平台进行验证。结果表明，放电脉冲通常发生在电压波形的峰值处，但随着谐波幅值的增大，也会出现在电压波形的其他区域。当谐波幅值为直流电压的5%～20%以及叠加谐波次数为6、12、18 时，放电脉冲次数为2～9 次。放电脉冲数随谐波次数及相对幅值的变化如图8所示。

图8 放电脉冲数随谐波的次数及相对幅值变化Fig.8 Change of PD pulse number with harmonic superposition times and harmonic amplitude

从图8 可以看出，放电脉冲数随着谐波相对幅值和谐波阶次的增加而增大，进而导致放电活动增强，加速绝缘老化，绝缘寿命缩短。

2.3 气压的影响

随着直流系统在航空领域的广泛应用，引起了人们对绝缘材料在高空和恶劣环境下受局部放电影响而导致退化的担忧。T SHAHSAVARIAN 等[71]研究了航空系统中常用的高温绝缘材料在正、负直流电压下的局部放电特性，并深入讨论了大气压对局部放电的影响。结果表明，在正极性电压下，自由电子向正极迁移，放电轨迹与场强大的高压电极相邻；在负极性电压下，高迁移率的负电荷促进了放电发展。此外，在低气压条件下总放电量高于标准大气压下的放电量，相对于正极性电压，负极性电压下的差异更显著。LI H L等[72]分别使用30%三氟碘甲烷/70%CO2和4% C4-全氟氮化物/96%CO2混合气体替代高压直流绝缘系统中的气体，研究在正、负直流电压和不同气压（0.1～0.5 MPa）下的局部放电起始电压。研究表明，在正极性和负极性直流电压下，局部放电起始电压均随着气压的增大而增大。在相同时间间隔和气压下，负直流电压产生的电流脉冲幅值高于正直流电压下产生的电流脉冲幅值。

2.4 缺陷的影响

电力设备绝缘在生产、运输、安装和运行中可能会形成绝缘缺陷，因此关于不同绝缘缺陷的直流局部放电发展过程和放电特性的研究引起了众多学者的关注。ZHU Y F 等[73]利用COMSOL 模拟了直流电压下交联聚乙烯中4 种典型绝缘缺陷（尖刺缺陷、气隙缺陷、划痕缺陷、外半导体层断口处台阶气隙缺陷）的电场分布和局部放电。结果表明，不同类型的缺陷会导致不同的电场畸变，其中尖刺缺陷下的电场畸变最严重，外半导体层断口处台阶气隙缺陷下的电场畸变最轻微。尖刺缺陷的放电重复率最大，其放电幅值与划痕缺陷的相似，而外半导体层断口处台阶气隙缺陷因电场畸变很小，放电重复率最低。通过以上结论验证了仿真结果与实验结果的一致性。杜浩等[74]采用实际运行的电缆制作了绝缘内部气隙、尖刺缺陷、外半导体层断口处台阶气隙缺陷3 种典型缺陷类型，并研究直流电压下含典型绝缘缺陷电缆的局部放电特性。结果表明，尖刺缺陷的放电起始电压最低，放电幅值最大，放电次数最少；断口缺陷的放电起始电压最高，放电次数最多，放电重复率呈现先增大后减小的趋势；内部气隙缺陷放电发展过程中存在“放电死区”，不同的放电量-时间间隔（Q-t）图谱呈“山丘状”，放电幅值最小。

3 目前研究存在的不足

局部放电的数值模拟方法需要考虑自由电子生成、放电发展和表面电荷衰减等几个物理过程。这些物理过程由各种方程和逻辑表达式定量描述，为此需要分配大量的参数值。参数值的选取可能需要大量的计算或测量，有些甚至是基于其他放电类型获得。此外，有些研究人员定义的参数值可能偏离了物理本质，还有的在数值模拟过程中使用了多个自由参数，不同的参数设置获得了类似的结果，导致研究人员对某些物理现象的原因产生误解。因此应减少模型中自由参数的数量，谨慎合理地选取相关参数，有助于避免得出错误的实验结论。

局部放电活动具有“记忆”特性，主要表现在先前放电产生的残余电荷会对后续放电产生影响。在恒定直流条件下残余电荷释放缓慢，对放电的影响尤其显著。残余电荷通过影响气隙内的电场并提供额外的自由电子来影响后续的放电特性，可能会导致放电加剧，进而加速绝缘材料老化，老化可能引起放电缺陷的永久变化，如气体成分、气隙表面的物理和化学特性[75]，该程度的影响称为永久记忆效应。其中，气体成分的变化主要归因于气隙中电负性气体的消耗和其他气体成分的生成；气隙表面物理和化学特性的变化主要表现在表面电导率和粗糙度的增加、液体或固体副产物的沉积[76-78]，从而导致气隙内气压的变化以及表面发射特性的改变。因此，有必要在数值模拟方法中考虑绝缘老化引起的气体成分、气隙表面粗糙度及固体或液体副产物等对放电特性的影响。

本文介绍的3种模型已经被众多学者用于研究不同绝缘缺陷的局部放电特性，并对建立的模型进行了实验验证，评估了模型与实验结果的一致性。但也有学者对所应用的模型只给出了仿真分析结果而并没有给出实验验证。因此，在后续工作中有必要继续运用实验来进一步验证模型的有效性以及探究模型的广泛适用性。