SiC逆变器供电的牵引电机匝间绝缘性能评估
2024-04-27罗英露赵安然于超凡林沐泓黄文冬
罗英露,赵安然,王 鹏,于超凡,林沐泓,黄文冬,彭 增
(1. 中车株洲电力机车研究所有限公司,湖南 株洲 410002;2. 四川大学 电气工程学院,四川 成都 610065)
0 引 言
电力电子装置可实现一次能源的高效转换,是高速铁路机车变频牵引电机驱动系统的核心设备。随着科学技术的发展,变频牵引电机朝着大功率的方向不断发展,对于半导体的要求越来越高,传统的Si 半导体已无法适应当前工业发展的速度。近年来,碳化硅(SiC)、氮化镓(GaN)等第三代宽禁带半导体器件的出现,有望使电力电子器件开断频率和可承受工作电压提高10 倍、体积缩小至原来的1/40、能量密度及热导率大幅度提升、开断时间降低至100 ns 以下,从而解决制约电力电子发展的瓶颈问题[1-2]。
作为交流传动牵引机车的核心设备,变频牵引电机绝缘的可靠性直接影响着整个机车的安全,而变频牵引电机绝缘承受逆变器产生的快速变化的脉宽调制(PWM)电压,在服役期间易发生局部放电,从而造成绝缘老化加速,引发安全事故[3-4]。随着SiC 等性质优良的第三代半导体在地铁牵引系统中的应用,地铁牵引系统的电压转换速率(上升时间)和工作频率将由Si 基逆变器的3 000 V/µs、500 Hz 提升至9 000 V/µs、2 kHz(未来可能进一步提升至5 kHz),由此引发的变频电机绝缘问题亟需探究。目前日本的新干线N700S车辆以及Bombardier公司参与制备的斯德哥尔摩地铁已开始使用SiC 逆变器驱动,国内从2019 年开始研究SiC 牵引系统的使用,所研发的牵引逆变器已在深圳地铁线等进行试行考核。
然而采用SiC 逆变器驱动的变频电机绝缘系统工作在高频、短上升时间的脉冲电压下,绝缘承受更加严酷的电、热应力,失效现象时有发生[5]。根据报道及相关研究,绝缘失效多数始发于匝间绝缘最后延伸至主绝缘[6]。针对变频电机匝间绝缘性能,A CAVALLINI 等[7-8]利用双绞线材料模拟变频电机匝间绝缘,检测其在方波电压下的局部放电起始电压(PDIV),探讨了频率对PDIV 和重复局部放电起始电压(RPDIV)的影响。结果表明,频率增大,RPDIV 随之降低,但对PDIV 没有影响。A RUMI 等[9]研究发现,在高温下,浸渍双绞线的PDIV 比未浸渍双绞线的PDIV 更低,这可能与温度变化、介电常数的改变有关系。针对上升时间对双绞线PDIV 的影响,A RUMI 等[10]认为上升时间过短引起的过电压,其有效持续时间也较短,因此PDIV 测试结果偏高。在上升时间较长时,PDIV 测试结果与正弦测试结果基本一致。HU Boxue 等[11]研究了在不同高电压变化速率(dV/dt)下电机定子绕组的局部放电,主要从改变脉冲的宽度和上升时间的角度出发,并拟合出经验公式,认为随着脉冲宽度的增长,PDIV 逐渐减小后趋于不变。目前,大多数学者在对变频电机匝间绝缘进行研究时,所采用的试样多为低压散绕试样,研究对象局限于PDIV。然而,随着SiC 的应用,高速机车内电机绝缘倾向II型绝缘结构,要求其在服役期间具备承受一定电应力的能力。此外,随着频率和dV/dt的提高,将增加绝缘结构介质损耗,更易造成电机端部过电压,加剧绝缘系统内电压分布不均度,进而诱发局部放电,加速绝缘老化。目前,尚没有理论表明匝间绝缘或加厚匝间绝缘能适应SiC 逆变器输出的更高dV/dt和更高开关频率的电压波形。
因此,本文通过模拟Si 逆变器和SiC 逆变器在不同工况(不同上升时间、电压峰峰值、频率)下牵引电机端部的电压波形,并测量高压变频电机电磁线的PDIV 及耐电晕寿命曲线,希望为变频牵引电机绝缘系统的开发和验证工作提供参考。
1 试 验
1.1 试验平台
重复脉冲电压绝缘检测平台如图1 所示,系统由高压脉冲电源、高压探头、特高频天线、示波器、高通滤波器、击穿保护器、烘箱及真空箱组成。
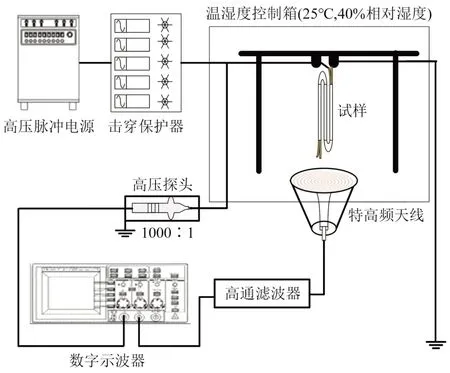
图1 重复脉冲电压绝缘检测平台Fig.1 Repetitive impulse voltage insulation test platform
高压脉冲电源参数信息如表1 所示,输出的脉冲电压用于模拟变频电机的实际工况。特高频传感器用于检测局部放电信号,在进行测试前,采用特高频天线检测电力电子开断信号。电力电子干扰信号频域分析如图2 所示,可以看出电力电子开断所产生的干扰集中在较低频段。根据文献[12-13]可知,局部放电的频域能量分布在0~2 GHz,而电力电子干扰则在500 MHz 以下,因此,采用信号处理模块滤除掉500 MHz 以下的信号能够消除电力电子器件产生的干扰。击穿保护器能够在试样击穿时断开加压回路,同时记录试样寿命时间。在进行PDIV 测试时,试样两端电压由0 V 开始,以50 V/s 的升压速率进行升压,直至检测出局部放电(信号阈值设置为5 mV)后停止升压,此时试样两端的电压幅值记录为PDIV。在进行耐电晕寿命测试时,快速升压至试验设置电压,激发局部放电并记录试样从施加该电压至击穿的时间为耐电晕寿命。

表1 高压脉冲电源参数Tab.1 High voltage pulse power supply parameters

图2 电力电子干扰信号频域示意图Fig.2 Frequency domain diagram of power electronic interference signal
1.2 试样处理
高压成型电机绕组主要由漆包扁线组成,本文采用MYFCRB-23 型(绝缘厚度为0.23 mm)和MYFCRB-30 型(绝缘厚度为0.30 mm)背靠背扁线(生产厂家为中国中车株洲研究所)模拟存在气隙的高压变频电机匝间绝缘,试样如图3所示。其中MYFCRB-23 型为主要研究试样,MYFCRB-30 型为厚度对照组。试验前采用无水酒精对其进行预处理,去除表面杂质,然后将试样置于烘箱烘烤24 h,消除水分。为排除偶然因素对试验的影响,每组试验均至少在相同的条件下测试5 个试样,每个试样测试5次。

图3 漆包扁线试样Fig.3 The enamelled rectangular wire sample
2 不同工况下的局部放电起始电压及绝缘寿命
2.1 不同频率下的局部放电起始电压及绝缘寿命
2.1.1 不同频率下的局部放电起始电压
与传统Si 基半导体相比,采用SiC 逆变器驱动的变频电机绝缘承受频率更高的脉冲过电压冲击,更易引发局部放电并加速电机绝缘老化,导致电机绝缘过早失效[14]。本文选择开关频率为2、6、10 kHz的高频重复方波电压波形(由宽禁带半导体固态开关对正、负直流电源进行切换产生),试验过程中保证环境温度为180℃,排除其他环境因素的影响。
局部放电具有随机性,其发生部位与PDIV 值并不确定,因此采用箱线图对局部放电起始电压进行统计研究,对每个试样的5次PDIV值结果取平均值,得到不同频率下PDIV测试结果如图4所示。从图4可以看出,随着频率的改变,高压变频牵引电机匝间绝缘的PDIV 并不会发生较大变化,PDIV 值基本集中在2.8~2.9 kV,因此改变开关频率对变频电机绝缘系统的PDIV几乎无影响。

图4 不同频率下的PDIV测试结果Fig.4 PDIV test results at different frequencies
2.1.2 不同频率下的绝缘寿命
设置上升时间一定,电压峰峰值为10 kV,环境温度为180℃,得到不同频率下耐电晕绝缘寿命测试结果如图5 所示。由图5 可知,随着频率升高,绝缘寿命减小。其中,10 kHz 下的耐电晕寿命约为63 min,比2 kHz 下的耐电晕寿命下降了89.8%。采用威布尔分布对本批试样的特征值寿命进行统计定量分析,威布尔可靠性函数由式(1)所示[15]。
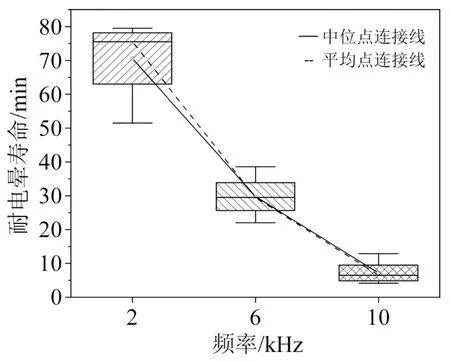
图5 不同频率下的耐电晕绝缘寿命测试结果Fig.5 Endurance life test results at different frequencies
式(1)中:α为失效概率为63.2%对应的参数,即尺度参数;β为形状参数;t为故障发生时间,min。
2.1.3 不同频率下的寿命模型
不同频率下,电压-频率具有联合老化寿命模型[16],可由式(2)表达。
式(2)中:L为耐电晕寿命,min;C、n、m为由实验数据拟合所得常数;V为电压峰峰值,kV;f为频率,kHz。
采用该模型对不同频率下的耐电晕绝缘寿命进行拟合,在试验中应控制其余重复方波参数及环境条件一致,由于该联合老化模型中V-n为定值,则该模型可简化为式(3)。
式(3)中,C0为实验数据拟合所得常数。
通过曲线拟合得到不同频率重复方波电压下的绝缘寿命,满足反幂函数规律,拟合结果如图6所示。
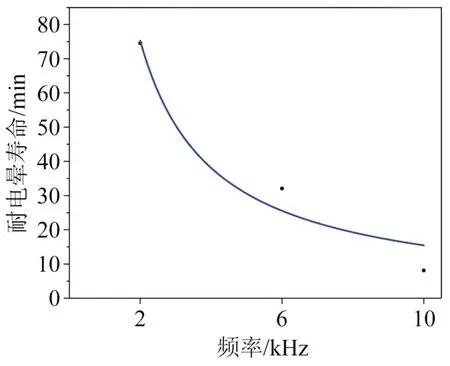
图6 不同频率下的绝缘寿命模型Fig.6 Endurance life model at different frequencies
由图6可得不同频率下的耐电晕寿命模型如式(4)所示。由图6 可以看出,随着频率的上升,变频牵引电机匝间绝缘的耐电晕寿命减小。虽然在不同频率下的实际耐电晕寿命值与模型预测值具有一定的差异,但是由于威布尔分布考虑的是失效概率为63.2%时的特征寿命,其具有一定的置信区间,该经验拟合模型能够较好地表征频率变化所引起的变频牵引电机匝间绝缘耐电晕寿命变化。此外,在实际工业应用中也应当充分考虑可能由于预测误差引起的安全威胁,因此在预测结果的基础上,应当考虑留有一定的裕度再进行工业生产。
在实际应用中,采用增大频率对绝缘寿命进行测试后,往往需要根据高频下的测试结果对低频条件下的绝缘寿命进行折算,该过程在工业中要求尽量简单可靠,故引入频率加速系数af,如式(5)所示。
式(5)中:L0表示样品在2 kHz 重复方波电压下的寿命;Lf表示在频率为f下的寿命。
根据不同频率下的耐电晕绝缘寿命测试结果,结合式(5)可计算得到10 kHz 和6 kHz 下的频率加速系数分别为9.16和2.32。在工业应用中一般考虑先使用频率之比,依据已有数据对不同频率下绝缘寿命进行初步近似预估,在数据量充足的情况下,可利用电压-频率联合老化寿命模型缩小误差。本试验中,10 kHz 下的加速系数明显与频率之比不相符合,造成此类现象的原因可能是在10 kV 高频高压耐电晕老化测试中,由于试样间存在相互差异,其本身存在一定的估算误差;再者依据工业估算,以2 kHz 为基准时10 kHz 下的耐电晕寿命应为14.81 min,这从数值上与试验结果对比差别并不大,因此在工业应用中采用频率之比进行寿命估算依旧可行。
2.1.4 不同频率下的局部放电特性
对绝缘寿命的考核研究主要是通过施加超过PDIV 的电应力来激发局部放电,从而导致材料快速降解,因此对于耐电晕寿命的分析可通过分析局部放电行为来进行。为量化不同参数条件下局部放电的统计特性变化趋势,对部分重要放电特征参量的变化进行了统计,包括:①最大放电幅值,指200 个局部放电周期内所监测到的最大局部放电脉冲幅值;②平均放电幅值,指200个周期内监测到的所有局部放电脉冲幅值的平均值;③单周波放电次数,指200 个局部放电周期内的局部放电总次数与周期数的商;④单周波总放电幅值,由平均放电幅值与单周波放电次数相乘得到;⑤单位时间内放电次数及总放电幅值,重复方波下发生的局部放电可通过特高频天线对空间电磁波进行捕捉得到,同时示波器对波形保存需要一定时间,因此认为在示波器保存时间间隔一致的情况下,单周波放电次数与总放电幅值在一定程度上能够表征单位时间内放电次数及总放电幅值。
不同频率条件下放电特征参量变化趋势如图7所示。从图7可以看出,随着频率的升高,平均放电幅值与最大放电幅值均呈现减小趋势;相反地,随着频率的升高,单周波局部放电次数逐渐升高。研究表明绝缘的受损程度与局部放电幅值、次数具有极大关联,然而局部放电次数与幅值随着频率变化呈现相反趋势,因此采用简单的局部放电次数与幅值评估绝缘在该频率重复方波波形下的损伤程度是不合理的。单位时间总放电能量可通过单周波总放电能量得到,结合局部放电次数与幅值的影响,得到不同频率下单周波及单位时间总放电能量如图8 所示。从图8 可以看出,随着频率的升高,单周波放电总能量呈现下降趋势,但单位时间总放电能量呈现增大趋势,表明对绝缘的破坏性变大。
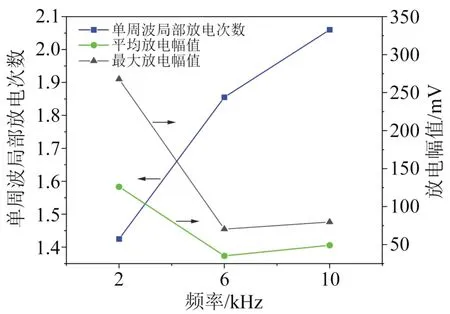
图7 不同频率下局部放电的幅值及次数Fig.7 The amplitude and number of partial discharge at the different frequencies
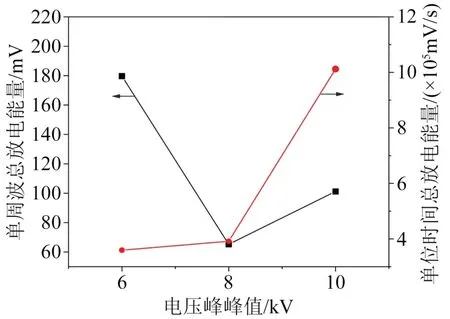
图8 不同电压峰峰值下单周波及单位时间的总放电能量Fig.8 Total discharge energy of a single cycle wave and unit time at different peak-to-peak volage
2.2 不同电压峰峰值下的绝缘寿命
2.2.1 不同电压峰峰值下的绝缘寿命
控制电压转换速率一定,电压频率为2 kHz,改变电压峰峰值分别为6、8、10 kV,环境温度为180℃,进一步测试不同重复方波电压波形下试样的耐电晕寿命,结果如图9 所示。从图9 可以看出,随着外加电压峰峰值的增加,高压变频牵引电机匝间绝缘的耐电晕寿命减小,且呈现明显的非线性关系。

图9 不同电压峰峰值下的耐电晕寿命Fig.9 Endurance life under different peak-to-peak voltage
2.2.2 不同电压峰峰值下的寿命模型
绝缘材料由高分子聚合物组成,其主要化学键键能如表2所示。电子运动的剧烈程度与外加电压峰峰值呈正相关,当外加电压峰峰值较大时,局部放电幅值很大,高速运动的电子直接轰击绝缘层,由于电子动能较大,在轰击绝缘层时,构成绝缘层组分的分子链将很容易被破坏,加剧绝缘结构的破坏。
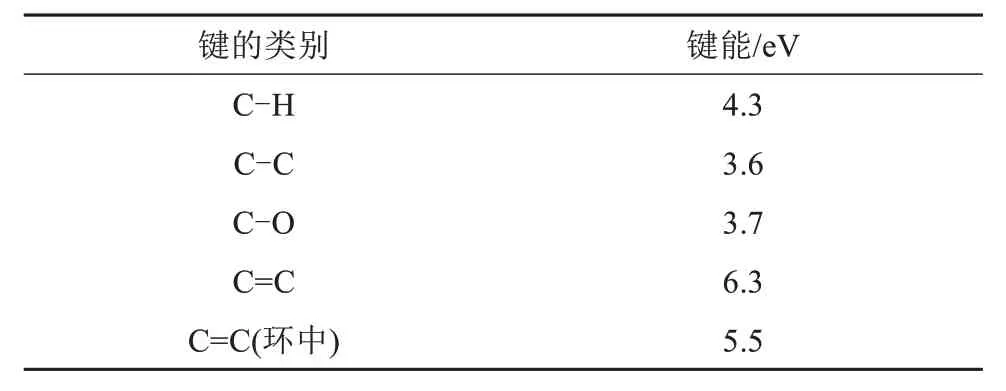
表2 聚合物中常见的化学键及其分解所需要能量Tab.2 Common chemical bonds in polymers and the energy required for their decomposition
利用式(5),以6 kV 下绝缘寿命为基准计算电压加速系数,结果发现8 kV、10 kV 下加速系数分别为2.31、7.04,并不满足线性关系,因此采用以电压峰峰值之比作为加速系数的方法是不可行的。根据IEC 60034-2020提出了一种普适的不同电压峰峰值下耐电晕寿命的反幂模型,可以很好地对不同电压峰峰值下的寿命情况进行模拟,其公式如(6)所示[17]。
式(6)中:n为耐久系数,为常值;L为试样耐电晕寿命;U为施加于试样两端的电压峰值;k为由试验数据拟合得到的常数。
通过拟合得到不同电压峰峰值下的耐电晕寿命模型如图10所示,可以看到不同电压峰峰值下的耐电晕寿命十分契合反幂模型,其相关系数为1。结合图10 计算得到试样在不同电压峰峰值下的耐电晕反幂模型公式如式(7)所示。采用该模型可为试样在其余电压峰峰值下的耐电晕寿命预测提供一定的帮助。

图10 不同电压峰峰值下的绝缘寿命Fig.10 Endurance life under different peak-to-peak voltage
2.2.3 不同电压峰峰值下的局部放电特性
图11 为不同电压峰峰值下的局部放电放电幅值及次数。由图11可知,随着试样两端外加重复方波电压幅值的增大,最大放电幅值与平均放电幅值逐渐增大,两者呈现相同的变化趋势。在电压由6 kV 提升至10 kV 时,平均局部放电幅值出现了微小的上升,最大放电幅值的变化相对更加明显。同时,随着重复方波电压峰峰值的增大,单周波局部放电次数减小。图12 为不同电压峰峰值下单周波及单位时间的总放电能量。由图12可知,单周波放电总能量与单位时间总放电能量随电压峰峰值的增大而增加,由此可知,单次放电能量增大。
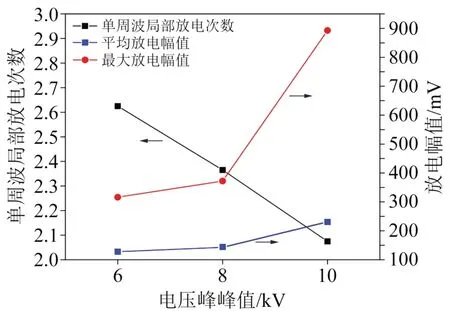
图11 不同电压峰峰值下局部放电的幅值及次数Fig.11 The amplitude and number of partial discharge at different peak-to-peak voltage
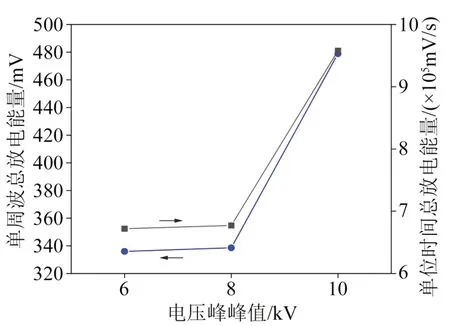
图12 不同电压峰峰值下单周波及单位时间的总放电能量Fig.12 Total discharge energy of a single cycle wave and unit time at different peak-to-peak voltage
2.3 不同上升时间下的局部放电起始电压及绝缘寿命
2.3.1 不同上升时间下的局部放电起始电压
电压上升时间对电机绝缘具有至关重要的影响。对于整机而言,其电路参数复杂,上升时间改变会使电机内部产生电压分布不均的情况。通过实际测量,一般电机首端线圈以及线圈的前几匝承受了最高电压峰峰值,L GUBBALA 等[18]通过等效电路仿真分析得到了同样的结果。研究使用高压成型扁线对来模拟高压变频电机匝间绝缘,该匝间绝缘试样在电路中呈现容性,且整机内无复杂电感环境,因此需要通过直接在试样两端施加不同上升时间的电压波形,对其实际工作中所承受的电应力进行模拟,以检验其绝缘性能。
固定电压频率与外界环境参数不变,设置环境温度为180℃,控制电压峰值一定,改变上升时间分别为500、670、1 000 ns对试样进行PDIV 测试,结果如图13 所示。从图13 可以看出,电压上升时间在500、670、1 000 ns 变化时,匝间绝缘试样的局部放电起始电压并未呈现显著的变化趋势,仅在较小范围内发生波动。这说明上升时间的变化会造成气隙内部的电场情况发生改变,因此对于耐电晕绝缘寿命会产生一定的影响。同时在对整机匝间绝缘进行PDIV 测试时,由于试样由容性变为感性,上升时间的变化会造成整机内部电压分布情况发生变化,从而影响PDIV测试值。
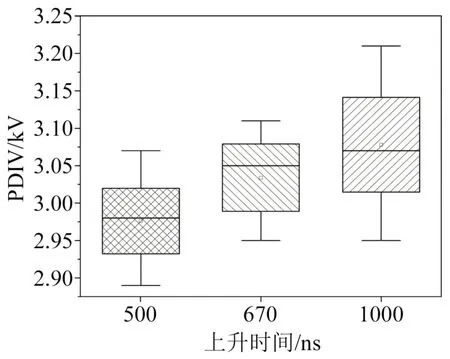
图13 不同上升时间下的PDIV结果Fig.13 PDIV results under different rise time
2.3.2 不同上升时间下的耐电晕寿命
在采集局部放电信号后增添试样,控制电压峰峰值为10 kV,频率为2 kHz,环境温度为180℃。由于试样电容一定,通过改变充放电电阻,分别施加上升时间为500、670、1 000 ns 的电压波形直至击穿,得到试样耐电晕寿命如图14 所示。由图14 可见,500 ns、670 ns下的耐电晕寿命几乎一致;当上升时间由670 ns 延长至1 000 ns 时,1 000 ns 时耐电晕寿命较前者增长了63.2%,增幅约为52 min。由此可见,电压上升时间对试样耐电晕寿命具有一定影响,在电压上升时间较大时,由于电压变化速率较小,局部放电能量相对较小,耐电晕寿命变长。

图14 不同上升时间下的耐电晕寿命Fig.14 Endurance life at different rise time
2.3.3 不同上升时间下的局部放电特性
图15 为不同上升时间下的局部放电幅值。由图15 可见,随着电压上升时间的增大,局部放电最大幅值变化不大,局部放电平均幅值随着电压上升时间减小也没有出现明显变化。因此,需要进一步监测单位时间内,不同上升时间条件下局部放电次数进行综合分析。文献[19]研究了100 ns 下电压上升沿时间的下降对于局部放电幅值的影响,发现局部放电幅值随着上升时间的缩短而增大,进一步验证了本文观点;文献[20]研究了在上升沿较长时(200~600 μs)的局部放电变化趋势,结果表明,随着上升时间的减小,局部放电幅值总体呈现为增大趋势。在衡量局部放电对绝缘的损伤时,除放电幅值外,局部放电次数也起到了重要作用,将单位时间局部放电次数与局部放电总能量绘制于图16中,结果发现随着电压上升时间减小,局部放电次数显著增加,但670 ns 下的局部放电次数大于500 ns 下的局部放电次数,同时单位时间内总放电能量与次数变化呈现相同的变化规律。总体上,随着上升时间减小,局部放电幅值与次数均呈现一定的上升趋势。

图15 不同上升时间下的局部放电幅值Fig.15 Partial discharge amplitude at different rise time

图16 不同上升时间下的单位时间局部放电次数及放电总能量Fig.16 Partial discharges number and total discharge energy per unit time at different rise time
2.4 不同温度下的局部放电起始电压及寿命
2.4.1 温度对PDIV的影响
研究表明,环境温度对绝缘层化学反应速率具有一定影响,导致绝缘材料的结构发生改变,造成其电荷累计效应、介质损耗发生变化,进而导致其局部放电起始电压与局部放电统计特性有所不同[21-22]。
控制电压上升时间为670 ns,占空比为50%,频率为2 kHz,改变温度分别为150、180、200℃,从零开始缓慢升压直至出现局部放电,统计激发局部放电的最小电压为局部放电起始电压并绘制于图17中,添加常温常压下PDIV 测试组进行对照。由图17可知,随着温度从常温升高到150℃,局部放电起始电压下降;然而随着温度从150℃升高至200℃,局部放电起始电压出现回升现象,但仍然小于常温下的局部放电起始电压,此趋势与文献[23]中趋势一致。

图17 不同温度下PDIVFig.17 PDIV at different temperatures
由于在常温下进行PDIV 测试时,测试结果相对运行时偏高,需要通过安全系数n对其进行折算,以保证实际运行中的高压变频牵引电机不会出现局部放电。根据研究结果,本批试样的安全系数如式(8)所示(采用最小PDIV 值),即本批试样在常温下检测时应使用大于12.01%的安全系数进行相应折算,以保证绝缘安全。
2.4.2 温度对耐电晕寿命的影响
高压变频牵引电机在实际运行过程中温度普遍集中在150~200℃。控制电压上升时间一定,电压峰峰值为10 kV,频率为2 kHz,改变环境温度分别为150、180、200℃,在重复方波电压下对漆包扁线试样进行测试,得到不同温度下的耐电晕寿命如图18所示。
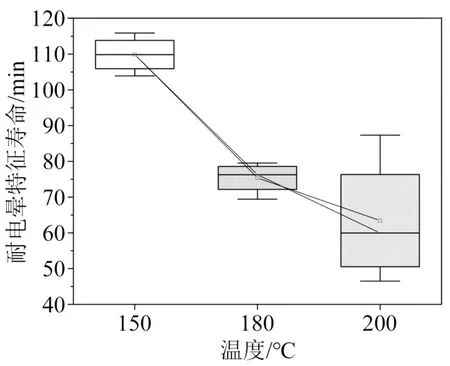
图18 不同温度下的耐电晕寿命Fig.18 Endurance life at different temperatures
从图18 可以看出,随着温度的升高,高压变频牵引电机匝间绝缘耐电晕寿命呈非线性递减趋势。其中,180℃、200℃时的耐电晕寿命比温度为150℃时的耐电晕寿命下降了约35 min 和50 min,下降幅度分别占150℃时的耐电晕寿命的32%和42%。可见,温度对试样耐电晕寿命具有较大的影响,为保证牵引电机在实际工况下的可靠性,应当在使用前根据其运行温度进行性能评估。
2.4.3 不同温度下的耐电晕寿命模型
当仅考虑温度变化时,随着温度的升高,绝缘的热老化速率变快。此时热老化的老化速度仅取决于化学反应速率,一般可用Arrhenius 方程表示,如式(9)所示[24]。
式(9)中:L为失效时间,min;T为温度,℃;Α、Β为常数,由化学反应的活化能确定。
学术界普遍认为,在纯热老化下绝缘寿命与在该温度下的化学反应速率成反比关系。根据“10℃减半原则”,当温度每升高8~12℃时,绝缘寿命将会缩短一半。由于高压变频电机匝间绝缘在实际工作中不仅会遭受热老化,也会承受一定的电热联合老化。G C MONTANARI 等[25-26]提出在Arrhenius方程的基础上应该考虑电应力的影响,该影响为外加电场的函数,可用f(Ε)进行表述,因此式(9)可用式(10)进行替代。
将不同温度下的耐电晕寿命以式(9)进行拟合并将结果绘制于图19中,得到匝间绝缘试样材料在不同温度、相同电应力加速条件下的加速模型如式(11)所示。由图19 可知,随着温度的升高,变频牵引电机匝间绝缘耐电晕寿命随之减小。在材料特性不发生明显变化的温度范围内,可以认为变频牵引电机匝间绝缘耐电晕寿命随着温度的升高呈现非线性减小趋势,该趋势满足考虑电应力条件下的Arrhenius 方程。因此,可以使用考虑电应力条件下的Arrhenius 方程对不同温度下绝缘结构或材料的耐电晕性能进行初始评估,为绝缘的设计提供指导思路。
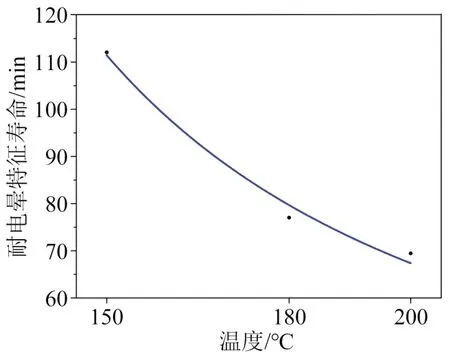
图19 耐电晕寿命模型的拟合曲线Fig.19 Fitting curve of endurance life model
2.4.4 不同温度下的局部放电特性
为进一步说明绝缘耐电晕寿命随着温度变化的原因,设置温度梯度分别为150、180、200℃,并在3 种不同的温度条件下采集在相同外加电压下200个周期的局部放电信号,得到不同温度下的局部放电特征参量和单位时间总放电能量分别如图20 和图21 所示。由图20~21 可以看出,随着温度的上升,单周波局部放电次数、最大放电幅值、平均放电幅值和单位时间总放电能量均增大。电热联合老化可能是高温绝缘失效的主要原因,需针对不同环境下的主导因素采取强有力的措施,以避免变频电机绝缘失效。

图20 不同温度下的局部放电特征参量Fig.20 Characteristic parameters of partial discharge at different temperatures

图21 不同温度下的单位时间总放电能量Fig.21 Total discharge energy per unit time at different temperatures
2.5 不同绝缘层厚度下的局部放电起始电压及寿命
2.5.1 不同绝缘层厚度下的PDIV对比
高压变频牵引电机绝缘失效事故中,匝间绝缘失效概率远高于主绝缘失效概率,然而,高压变频牵引电机匝间绝缘的破坏往往会引起主绝缘的破坏,同时在击穿过程中主绝缘常常出现严重碳化现象,而匝间绝缘却几乎完好,因此事后事故认定时,往往会忽略匝间绝缘失效而只考虑主绝缘失效[27]。从电机结构上看,匝间绝缘层较薄,接触面积大,在电机实际运行中过电压较高,因此往往发生绝缘过早失效。在工业应用中增加绝缘层厚度在一定程度上能够提升绝缘性能,然而由此导致的成本增加、工艺要求变高及空间利用率降低会造成更严重的经济损失与能源浪费,因此是否增加绝缘层厚度,取决于增加绝缘层厚度所带来的收益与支出的对比,寻找合适的绝缘层厚度对于工业生产应用具有举足轻重的作用。为探究厚度增加带来的绝缘性能改变,分别以0.23 mm 绝缘层试样(MYFCRB-23 型)与0.30 mm 绝缘层试样(MYFCRB-30 型)为研究对象开展试验,对比不同绝缘层厚度下的PDIV变化。
采用固定双极性方波对两种厚度绝缘层的高压变频牵引电机匝间试样进行测试,上升时间为670 ns,占空比为50%,频率为5 kHz,控制环境温度为180℃,测试结果如图22 所示。从图22 可以看出,随着绝缘层厚度的增加,局部放电起始电压明显提升。相比于0.23 mm 绝缘层试样,0.30 mm 绝缘层试样的厚度提高了30.4%,其最小局部放电电压则提高了36%,提升了1.2 kV。

图22 不同厚度绝缘层的PDIVFig.22 PDIV of insulation layers with different thickness
2.5.2 不同绝缘层厚度下的耐电晕寿命
不同的绝缘层厚度,其绝缘寿命表现是不同的。随着绝缘层厚度的增加,电机效率及槽满率下降,成本将会大幅度上升。工业上对于电机匝间绝缘要求具有一定的耐热性、耐油性和力学性能,同时对于匝间绝缘层厚度要求尽可能的小[28]。故在选取绝缘层厚度时,应充分考虑其性价比。本研究选取厚度为0.23 mm 与0.30 mm 的绝缘层匝间绝缘试样,对两者施加相同的电应力,控制电压峰峰值一致,占空比为50%,上升时间为670 ns,环境温度为180℃,设置电压峰峰值分别为6、8、10 kV,频率为2 kHz,上升时间一定,然后进行耐电晕测试,结果如图23所示。由图23可知,6 kV下的0.23 mm绝缘层试样的绝缘寿命约为472.5 min,0.30 mm 绝缘层试样的绝缘寿命约为1 105.5 min。绝缘层厚度的增加能够提升绝缘寿命。

图23 不同厚度绝缘层在不同电压峰峰值下的耐电晕寿命Fig.23 Endurance life of insulation layers with different thickness under different peak-to-peak voltage
2.5.3 不同厚度绝缘层下的耐电晕寿命模型
对于不同厚度绝缘层试样的绝缘失效,G C MONTANARI 等[29]将绝缘失效用数值化的方式进行定量描述,认为绝缘总寿命可用F进行描述,该变量是用来描述绝缘材料老化的性能p的函数,被描述为F(p),定义单位时间老化速率为g,当试样、环境参数及外加电压一定时,该老化速率可认定为常值。则绝缘总寿命与单位时间老化速率、失效时间之间的关系如式(12)所示。从图23可知,随着绝缘厚度的增加,绝缘总寿命增加。设绝缘总寿命变化系数为k,老化速率变化系数为n,根据特征寿命可知,计算得到k与m的比值约为2.34。对于厚度为0.30 mm 绝缘层的匝间绝缘试样,其在不同电压峰峰值下的绝缘寿命模型与2.2 节所述模型具有较高的吻合性,仅比例系数发生一定的变化。因此对于厚度为0.23 mm 与0.30 mm 的绝缘层试样耐电晕寿命(L0.23、L0.30),两者的关系可通过式(13)对耐电晕寿命进行描述。
2.5.4 不同绝缘层厚度下的局部放电特性
在3 个电压峰峰值下,不同厚度绝缘层试样的特征寿命值等效参数一致,以10 kV 外加电压为例,收集200 个10 kV 下不同厚度试样的局部放电周期进行局部放电特征参量统计,并对比分析不同厚度试样单位时间局部放电总放电能量的变化,结果如图24 所示。由图24 可知,随着绝缘层厚度的增加,单位时间内总放电能量减小,并且由于绝缘层厚度增加,其绝缘性能增强,因此随着厚度增加,绝缘性能可明显升高。

图24 不同厚度绝缘层的单位时间总放电能量Fig.24 Total discharge energy per unit time of insulation layers with different thicknesses
3 机理分析
3.1 不同参数下的PDIV分析
根据放电机理,局部放电发生需要满足两个条件[30]:
(1)电场需要大于局部放电起始电场,如式(14)所示。
式(14)中:Εt表示气隙所承受的瞬时场强;Εmin表示气隙发生放电所需要的最小场强。
(2)需要引发局部放电的初始电子。根据Richardson-Schottky 定律,表面电荷的积累更容易促使局部放电初始电子的出现,初始电子产生概率(λ)可由下述模型进行计算,如式(15)所示。
式(15)中:Ε为气隙处瞬时场强为ψ时产生电子所需的能量;ν0为光电离常数;qe为单位电荷;K为玻尔兹曼常数;T为温度;ε0为真空介电常数;Nsc为电荷数。
在重复方波条件下,在上升沿与下降沿处,由于极性翻转,气隙内电场强度超过局部放电起始电场强度,局部放电往往集中在上升沿与下降沿处。频率的变化并不会改变气隙,同时高压牵引电机匝间绝缘可以看作具有一定容值的电容器,假设其介电常数实部与介电常数虚部并不会发生变化,气隙中的电场可以等效为施加电压在开关机柜内部阻抗与负载上按照比例进行分压,因此频率的改变并不会影响PDIV。但实际上存在偶极取向的介质损耗,另外介电常数对频率的依赖性也必须加以考虑,因为偶极子取向不会发生在某些临界频率以上。考虑临界频率f=1/D处出现介质损耗峰值,其中D为偶极子的弛豫常数,那么在大于该临界频率的所有频率下,介电常数实部都会减小。而根据相关报道[31]变频电机绝缘材料的临界频率大于3 MHz,因此在当前测试频率(变频电机工作频率)下PDIV测试结果不变。
对于不同上升时间下的局部放电起始电压,目前IEC 60034-2014 规定应使用电压峰峰值作为PDIV 值而并非稳态电压,在采用匝间绝缘试样进行测试时,上升时间的改变并不会引起绝缘分压的变化,同时根据放电机理,上升时间并不会影响放电起始电场和初始电子产生概率,因此在统计学意义上,上升时间的变化并不会引起匝间绝缘试样PDIV 的变化。在本文中上升时间的改变造成绝缘PDIV 的微弱变化是PDIV 测试的偶然误差导致的。而对于整机测试,其测试的PDIV 不同主要是上升时间改变导致内部各绕组间分压不同造成的。
但是,随着温度的上升,介电常数发生变化,气隙电场强度增加,同时温度使空间电荷运动更剧烈,因而造成局部放电起始电压下降;而当温度达到150℃以上,局部放电电压随着温度升高而下降,原因可能是温度上升造成热胀冷缩,从而使气隙结构发生改变,造成放电位置发生变化,进而导致局部放电起始电压发生改变。
对于不同绝缘厚度的试样,绝缘层厚度的变化改变了气隙内部电场,因此随着绝缘层厚度的增加,气隙内部电场强度降低,PDIV升高。
3.2 不同参数下的耐电晕寿命分析
对于不同参数下的耐电晕寿命结果,可结合局部放电特性进行分析。
在不同频率下,虽然单个周期内放电次数增多、放电幅值减小,但是在单位时间内局部放电总能量增大,因此随着频率增加,耐电晕寿命降低。
电压峰峰值的增加虽然减少了单周期内放电次数,但提供了更大的电场强度,激发更剧烈的局部放电,此时电子崩内部的高能粒子增多,其动能超过表2 所示的聚合物化学键键能,通过碰撞能直接致使聚合物化学键断裂,因此,随着电压峰峰值的增加,局部放电能量呈现非线性变化趋势,对于绝缘的破坏作用呈现指数型上升趋势。
上升时间的变化会影响极性反转时气隙内部电场变化速率,从而改变局部放电的特性。随着上升时间的缩短,虽然在平均放电幅值上无太大变化,但其能够激发更多的局部放电,因此单位时间总局部放电能量增大,对绝缘的破坏作用增强。
绝缘层厚度的增加使得气隙长度与绝缘材料厚度之间的几何关系发生改变,从而影响了气隙内部电场强度,降低了单位时间内局部放电强度,同时绝缘厚度的增大也增强了绝缘耐电晕能力,使得绝缘材料的耐电晕寿命进一步提升。
4 结 论
(1)频率对PDIV 无影响,但是对耐电晕寿命具有重大影响。控制电压为10 kV,电压上升时间为670 ns,温度为180℃下,通过改变频率(2、6、10 kHz)进行耐电晕寿命测试,结果表明10 kHz下的耐电晕寿命比2 kHz下的耐电寿命下降了89.8%,约为63 min。因此在电机绝缘实际承受电应力可能超过PDIV 时,应当着重注意频率对耐电晕寿命产生的重大影响。
(2)电压峰峰值的变化会对耐电晕寿命产生较大影响,电压峰峰值与绝缘寿命呈现反幂趋势,若以6 kV下的耐电晕寿命为基准,电压峰峰值为8 kV时的耐电晕寿命相比减少了约315 min,约为66.7%;电压峰峰值为10 kV 时耐电晕寿命相比减少了约400 min,约为85.1%。因此应当考虑实际运行中最严峻的电应力条件下引发放电时其电压峰峰值不应高于PDIV值。
(3)电压上升时间对PDIV 无影响,但对耐电晕寿命具有较大影响。500 ns、670 ns下的耐电晕寿命几乎一致,但当电压上升时间延长至1 000 ns 时,与500 ns 的耐电晕寿命相比,其绝缘寿命增长率为63.2%,增幅约为52 min。
(4)温度对PDIV 具有一定的影响,由常温上升至150℃时,PDIV 降低了约300V;但当温度进一步上升至200℃时,PDIV 出现一定升高。在实际运行中应当考虑温度对试样老化分界线的作用。另外,温度对绝缘寿命具有较大影响,以150℃下的耐电晕寿命为基准,在180、200℃时的耐电晕寿命分别下降了约35 min 和50 min,下降值分别约占150℃下耐电晕寿命的32%和42%。
(5)绝缘厚度对PDIV 具有显著影响,MYFCRB-30 型试样的PDIV 测试结果比MYFCRB-23 型提高了36%,提升了1.2 kV。6 kV 下MYFCRB-23型试样的平均绝缘寿命约为472.5 min,MYFCRB-30 型试样的平均绝缘寿命约为1 105.5 min,厚度增加使耐电晕寿命大幅提升,因此可考虑增加绝缘厚度以提升试样的耐电晕寿命。
