基于IFM-KS模型的多层煤开采上覆岩层移动模型

程健维, 盛树平, 冉德志, 马永侦

(中国矿业大学 安全工程学院, 江苏 徐州 221116)

目前煤炭仍是我国能源的重要组成部分, 根据国家统计局数据显示, 2022年原煤年产量45.6亿t,占能源消费总量的56.2%。煤层开采后上覆岩层原始应力平衡被打破, 必然导致采空区上覆岩层发生垮落、弯曲, 引发沉降、离层等现象, 进而带来冲击地压、地表沉陷、岩层内部流体(水、瓦斯等)渗流等安全与环境问题[1]。岩层移动是发展科学采矿的技术基础, 研究岩层破断前后的力学行为, 揭示岩层移动规律, 对煤矿安全高效开采具有重要意义[1–2]。

在岩层移动研究领域, 国内外诸多学者进行了理论研究和实际应用, 并取得了丰硕成果。刘天泉[3]基于对采空区上覆岩层在采动影响下的移动和破断规律的研究, 提出了采空区“竖三带”、“横三区”理论, 对于上覆岩层裂隙活动的研究做出了重大贡献; 钱鸣高[4–5]等在采空区上覆岩层裂隙活动规律研究的基础上, 提出了关键层理论, 研究了在关键层作用下上覆岩层的变形、离层及破坏规律, 并通过运用模型试验、图像分析和离散元模拟的方法, 研究了采场上覆岩层裂隙演化的分布特征, 提出了采场“O”型裂隙圈理论。此外, 关于单层煤开采上覆岩层移动模型的推导、岩层沉降系数模型以及关键参数的计算方法等方面, 也有诸多学者进行了深入研究。刘宝琛[6–7]等引入了随机介质理论并发展为概率积分法, 该方法已成为最受欢迎的方法之一, 并被广泛应用于开采沉陷预测领域; 谢和平[8]等采用S-R分解应变定义, 提出了几何非线性和物理非线性的连续性介质模型对岩层移动定性和定量预测; 左建平[9–10]等通过模拟采空区顶板破断, 分析了不同厚度岩层的破断模式, 建立了采动岩层移动“类双曲线”模型和内外“类双曲线”模型; 程健维[11–15]等应用影响函数法, 考虑岩层变形力学特征及其层状结构的特点, 结合关键层理论, 提出了IFM-KS模型, 先后提出终态二维开采沉降预测模型、动态二维开采沉降预测模型、终态三维开采沉降预测模型, 并得到了广泛应用。

随着采矿技术水平的提升和浅埋煤层资源的枯竭, 煤炭开采逐渐向地下深部发展, 深部开采必将面临岩层二次扰动问题, 因此, 研究二次扰动后的岩层移动尤为重要[16]。上述研究推动了上覆岩层沉降预测理论的发展, 但对于双系煤层开采后岩层移动的研究相对较少。近距离开采, 煤层间距大于或小于冒落带高度, 均会导致导水裂缝带再扩展, 发育高度增加, 覆岩垂直应力集中系数降低,变形破坏加剧[17–20]。GHABRAIE[21]等考虑不同煤层堆叠关系等沉降参数, 提出了一种离散型影响函数法计算每层的最终沉降值, 并通过叠加获得最终沉降值; 王悦汉[22]等通过假定重复采动时碎胀减少量与初次采动碎胀量成正比, 提出了预测重复采动条件下下沉系数的计算式, 并与现场实测与公式对比证明了其正确性; 秦严[23]通过相似模型试验和数值模拟等方法, 对多层煤开采岩石破碎特性、煤层间距等方面进行研究, 指出多层煤采动会导致裂隙带高度增加, 煤层间距对沉降有较大的影响; 文虎[24]等进行了物理模拟试验和数值分析, 研究近距离两层煤开采的影响, 指出复动开采是导致裂隙沟通地表的主要原因; 刘世奇[25]、杜君武[26]等提出重复采动下导水裂缝带和垮落带高度预测应当考虑煤层的采高、煤层的间距和煤柱等, 通过物理相似模拟和数值模拟的方法分析了覆岩移动破坏规律, 并在实际工程应用中验证了模拟结果的合理性; SUI Wanghua[27]等讨论了煤层间距和下煤层厚度对双系煤层开采的影响, 结果表明当(M,h/M)(h指煤层间岩体的高度,M指下煤层的开采高度)位于分界线以下时, 重复采动对塌陷和导水裂缝带的发育影响较大, 需要考虑相互作用的叠加, 在分界线以上时可以忽略相互作用, 按单层煤开采计算破坏高度。此外, 空隙率可以定量表征采场裂隙分布,是描述瓦斯运移规律的关键参数[28–29]。WANG Gang[30]等通过相似模型试验和数值模拟, 定量判断裂隙带的高度, 通过现场验证其有效性和可靠性, 并探讨了应力比和顶板强度对裂隙带高度和渗透率的影响规律。对于这些研究主要采用数值模拟和相似试验结合的方法, 以试验总结规律为主。

针对双系煤层开采对岩层移动所带来的影响,笔者将重点聚焦煤层间距对岩层移动的影响特性。通过将多次扰动后的岩层移动与煤层间距建立联系, 从而将IFM-KS模型推广到双系煤层开采,建立复采条件下终态二维沉降预测模型, 揭示双系煤层开采后上覆岩层移动规律, 并结合岩层移动模型进行空隙率的计算, 对比单层煤开采, 分析双系煤层开采时空隙率的变化规律, 探讨采空区是否沟通形成复合采空区。该模型可为开采煤层群或近距离煤层时, 研究二次扰动的岩层沉降提供理论参考, 对煤矿安全生产、地表建筑物防护以及岩层移动研究提供重要理论参考和实践价值。

1 单层煤开采上覆岩层移动模型

煤层开采后, 其上覆岩层运动必然具有层状特点[1]。地下不同岩层, 所受载荷、强度不同, 因此,IFM-KS模型考虑了岩层的岩性及关键层的作用,按自然岩层划分计算不同岩层的沉降值, 依次计算每一岩层的垂直位移、水平位移量, 得到岩层移动的位移曲线[31–32]。该方法适用于连续性的岩层, 由于垮落带不具有层状结构, 不适用于垮落带的岩层移动研究。岩层沉降模型计算步骤如下:

(1)收集地质柱状剖面图, 从下至上命名1, 2,3, …,n层, 如图1所示。

图1 采区平面上覆岩层Fig.1 Overlying strata on the mining area plane

(2)定义影响函数。对每一层岩层进行垂直和水平运动的计算, 垂直位移、水平位移影响函数公式为

式中,fs为垂直位移;fu为水平位移;m为煤层开采厚度;ai为地层的沉陷系数;iR为主要影响半径;x'为局部坐标系预测点的横轴坐标;zi为预测点在全局坐标系的纵坐标。

(3)对影响函数积分。预测点(x',zi)处的垂直和水平位移是通过对第i层岩层左右拐点进行积分计算得到。为了方便使用影响函数,O–X坐标系的原点设置在采空区开切眼处,X方向为工作面走向方向,L为工作面推进长度, 如图2所示。假设预测点的坐标为x, 在工作面左侧拐点偏距(d1)和右侧拐点偏距(d2)区间内对影响函数进行积分, 积分域为Ls=[d1-x,L-d1-d2]。

图2 走向主断面最终沉降值预计原理Fig.2 Principle for predicting the final settlement value of the main section along the strike direction

基于影响函数法, 预测点的最终沉降值是开采煤层左右拐点偏距间的所有开采单元对该点所造成影响的叠加, 即沉降影响函数在积分域内的积分值。在图2中, 一小块宽度为dx的单元体的开采在预测点O′处诱发的沉降量为ds。当下一块单元体被开采时, 影响函数的中心将会移动到该单元体的位置并在预测点O′处诱发不同的沉降值。预测点的最终沉降值即为2个拐点偏距间影响函数曲线与坐标轴所围成阴影区域的面积, 最终沉降值的数学表达式为

式中,L为工作面走向推进长度;d为拐点的偏移距离。

与最终沉降值的预计相同, 预测点的最终水平移动值是开采煤层左右拐点偏距间的所有开采单元对该点所造成影响的叠加。最终水平移动值的数学表达式如式(4)所示, 其大小等于图3中阴影部分的面积。在图3中, 负值区域的面积大于正值区域的面积, 所以净面积为负值, 即预测点的最终水平位移为负值。

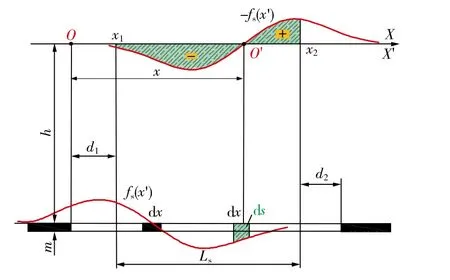
图3 走向主断面内最终水平移动值预计原理Fig.3 Principle for predicting the final horizontal movement value within the main section

2 双系煤开采上覆岩层移动模型

2.1 双系煤层开采岩层移动模型建立

针对单层煤开采模型, 预测点的沉降源自于下部开挖单元的影响叠加, 因此在预测点下方经历二次开挖时, 将受到2个开挖单元影响的叠加。在上层煤开采后, 产生的影响记为Su; 而进行下层煤开采时, 不仅煤层间的岩层受影响产生沉降位移, 上层煤覆岩在下层煤开采过程中也会受到干扰而产生沉降位移。在下层煤开采后, 煤层间预测点只受一次下层煤开采影响, 其沉降值记为Sd; 然而对于上层煤覆岩而言, 其受到二次开采影响, 预测点的位移为二次影响的累加。假设未开采上层煤, 仅开采下层煤时, 对上层煤覆岩产生沉降值Sd; 在上层煤开采后, 岩层的移动重新达到平衡, 形成复杂的铰链结构, 此时受下部煤层开采影响的沉降值不再是Sd, 记作bSd。双系煤层开采采区上覆岩层模型如图4所示。双系煤层开采后的沉降主要受下层煤开采的厚度、岩层的岩性、煤层重叠形态和煤层间距等因素影响。单层煤模型中已考虑了岩石力学特性和开采厚度等, 因此双系煤层模型重点考虑煤层间距产生的影响,b是关于煤层间距的经验系数, 则上层煤覆岩S2(x,zi)为

图4 双系煤层开采采区上覆岩层模型Fig.4 Overlying strata in the mining area of dual coal seams

式中,b为经验系数;S2为上层煤上覆岩层沉降值,受二次开采扰动;h1为上层煤埋深;h2为下层煤埋深。

有边界条件h2≫h1时, 即二次开采的煤层间距非常远, 可以认为二次开采对上煤层的上覆岩层不产生影响或影响非常小。将式(5)变换得到:

在煤炭开采过程中, 通常采用自上而下的顺序, 先开采上层煤, 然后开采下层煤, 那么只能观测到这两次开采后的沉陷值, 因此式(6)中的S2是未知数, 为二次开采后沉降的观测值,Su和Sd是模型计算值。结合所收集的多个实际案例和类似模拟计算案例的沉降数据, 通过回归分析进行拟合, 得到的拟合曲线如图5所示, 即

图5 拟合曲线Fig.5 Fitting curve

因此, 确定双系煤层开采岩层垂直移动模型为

式中,1S为层间岩层沉降值, 是受一次开采扰动影响后的沉降值。

相同的, 有双系煤层开采岩层水平移动模型为

式中,U1为层间岩层水平位移值, 是受一次开采扰动影响后的水平位移值;U2为上层煤上覆岩层水平位移值, 是受二次开采扰动影响后的水平位移值;Ud为上层煤开采时岩层水平位移;Uu为下煤层开采时岩层水平位移。

2.2 模型沉降参数

(1)地层沉陷系数ai

地层沉陷系数的影响因素包括深度、岩性、结构等, 都显著影响地表和地层的沉陷。从覆岩移动的案例中收集了148个沉陷系数, 通过回归分析得到的沉陷系数拟合曲线如图6所示, 拟合得到的经验公式[14]为

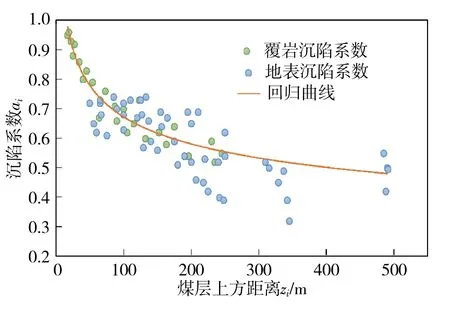
图6 沉陷系数回归分析拟合曲线[14]Fig.6 Regression analysis fitting curve of settlement coefficient[14]

(2)拐点的偏移距离di

拐点是曲线由凸变凹的临界点, 拐点的偏移距离即转折点到边缘的水平距离。其经验公式[12]为

(3)主要影响半径iR

从岩层移动盆地边缘到最近的充分沉降点之间的水平距离Li的一半即为主要影响半径Ri。为了确定特定岩层的影响半径, 可以将该岩层理想化为一个产生弯曲变形的固支梁模型, 左端固定于沉陷盆地边缘, 右端为最近的沉降量为Smax(zi)的点。根据材料力学的固支梁挠度计算公式, 可以得到岩层充分沉降值的表达式为

式中,Smax(zi)为岩层充分沉降值, m;qi为岩层上覆载荷, N;Ei为弹性模量, N/m;I为岩层断面惯性矩, m4;Li主要影响区域水平长度, m。

6.dabusu qami arun-a bui ɡebel ，dalai tenɡkis ba na arun-a要问盐是哪里来的，是从大海和湖泊里来的)

取固支梁岩层为单位宽度, 即长度为1 m, 则岩层的惯性矩Ii=h312, 岩层充分沉降值Smax(zi)=mai, 结合上式可以推导出主要影响半径Ri的表达式[33]为

根据关键层理论, 关键层可以承受部分或全部上覆地层的质量, 并控制部分或全部地层的移动。当关键层断裂时, 关键层上方部分或全部地层会同时下沉[34]。因此, 引入关键层理论来帮助关键层的荷载计算和判别, 确定上述各式中目标岩层所承受的载荷iq。假设煤层顶板上方存在m层岩层, 各岩层厚度为ih, 容重为ir。当关键层发生运动时, 由关键层控制的上覆岩层将同步移动, 形成类似组合梁的结构[35–36]。以煤层上方的第1层岩层为例, 其上覆载荷计算公式为

其中,

(qn)1为考虑到n层对第1层影响时形成的载荷。由此可得:

式(13)即为计算第1层岩层上覆载荷大小的公式。在实际计算各个岩层上覆载荷值时, 式(14)还可以用来确定上覆岩层中软硬岩层间产生的离层裂隙的位置。若第n层对第1层的载荷大于n+1层对第1层的载荷, 即(qn)1＞(qn+1)1, 则表明第n层岩层和第n+1层岩层之间会形成离层裂隙。因为第n+1层岩层可以承受较大的载荷, 将其视为关键层, 使得从n+1层以上的岩体载荷不会继续传递到其下的岩层之上[5,37]。

3 案 例

3.1 数值模拟研究方案

笔者通过UDEC软件数值模拟方法, 以具体案例为研究对象, 验证双系煤层开采岩层移动预测模型的合理性。

3.1.1 模型和参数设置

以某矿5106工作面为研究背景, 根据其地质资料及煤层柱状图, 沿走向方向建立模型。为了简化模型计算, 不考虑工作面支护的影响, 将具有相似岩石力学特性或厚度较小的岩层划分为一组, 共划分25组。岩块采用莫尔–库伦模型, 节理模型采用面接触的库伦滑移模型。模拟所采用的煤岩体力学特性参数为实测值, 具体参数见表1。

表1 煤岩体力学特性参数Table 1 Mechanical property parameters of coal and rock mass

3.1.2 模型边界条件设置

通过UDEC7.0软件所建模型长400 m, 高280 m, 煤和岩层共计25层, 重力加速度g为9.8 m/s2。模型左右边界施加位移约束, 即x=0,400 m边界的水平方向位移为0, 底部边界(y=0)显示垂直方向位移, 上部为自由边界。模拟模型如图7所示。

图7 模拟模型示意Fig.7 Schematic diagram of simulation model

3.1.3 模拟开挖方案

煤层开挖时, 左右两侧预留50 m宽, 具体开挖步骤:

①分步开挖上层的下1煤层, 开采高度4 m, 每次开挖50 m, 待计算平衡后, 开始下一次开挖, 开挖长度300 m。通过优化节理和网格参数, 减少模拟中位移与计算模型中位移的误差。

②保留优化参数, 分步开挖下5煤层, 开采高度9 m, 每次开挖50 m, 计算平衡后进行下一次开挖, 总开挖长度300 m, 研究岩层沉降情况。煤层开挖过程中监测上方组号20, 21, 22, 23岩层的移动情况, 即A, B, C, D监测线, 分别位于上层煤上方27, 34, 52, 118 m, 监测岩层移动情况, 并由history命令保存。

3.2 模型计算及其结果对比

上层煤和下层煤开采上覆岩层沉降云图如图8~9所示。由图8可知, 上层煤开采高度为4 m, 最大沉降值约为4 m, 其中, 前100 m的采动影响较为明显, 上覆岩层产生的位移约为3.5 m, 整体影响范围呈梯形。

图8 上层煤开采后上覆岩沉降值云图Fig.8 Cloud map of overlying rock settlement after upper coal mining

由图9可知, 在下层煤开采时, 垮落现象明显,煤层间岩层位移显著, 采动影响至上采空区, 加剧了上采空区上覆岩层的沉降, 造成上覆岩层“活化”, 产生明显位移, 影响范围扩大至地表, 影响范围呈梯形状。从开采过程来看, 当开挖距离超过50, 100 m时(图9(a)~(b)), 逐渐对上采空区产生较小的影响, 煤层间岩层在开采100 m时开始垮落; 当开挖距离为150, 200 m时(图9(c)~(d)), 煤层间岩层产生了显著的沉降, 沉降6~9 m, 对上采空区的影响范围进一步扩大, 局部区域沉降达到9 m; 在开挖距离为250, 300 m时(图9(e)~(f)), 影响范围向开采方向移动, 由于上方岩层载荷逐渐增大, 岩层发生垮落, 导致二次沉降、“活化”, 造成上采空区局部沉降范围扩大(图9(d)~(f)中黄色虚线), 其影响范围呈山峰状, 二次沉降约滞后工作面100~150 m。

图9 下层煤开采过程上覆岩层沉降值云图Fig.9 Cloud map of overlying rock settlement during lower coal mining process

运用MATLAB软件对双系煤层开采数学模型进行表达式计算, 采用Origin软件对计算结果进行处理, 绘制出煤层开采后测线A, B, C, D的沉降对比曲线, 如图10~11所示。各测线沉降值对比结果显示, 煤层开采后的沉降曲线呈现出良好的重合和相似趋势。

图10 下1煤开采后上覆岩层各测线沉降值对比Fig.10 Comparison of settlement of various measuring lines in the overlying strata after coal mining in lower 1

由图10可知, 上层煤开采后, 各测线在采空区两侧存在较大误差, 约为1 m, 是因为数值模型两侧悬臂梁未完全垮落, 而计算中考虑了主要影响半径与沉陷系数, 岩层与煤层距离越近, 垮落程度越高。测线C, D的整体沉降误差较小, 沉降曲线高度吻合, 但由于UDEC中岩层划分节理和工作面分步采动导致它们相互铰接, 沉降值有一定波动。其中, 在60, 80 m处的模拟沉降值均大于IFM-KS模型计算值, 在200~300 m处小于模型计算值。

由图11可知, 下层煤开采后, UDEC模拟的沉降曲线与模型计算曲线具有相似趋势, 但在两侧沉降值小于模型计算值, 在中间大于模型计算值。测线A, B, C的位移误差较小, 模拟与模型沉降曲线重合较好; 测线D的误差较大, 原因在于UDEC模拟中, 当关键层断裂时, 上覆岩层整体出现较大的沉降。而在移动模型中, 岩层沉降的计算充分考虑了关键层的作用, 特别是层间关键层对上覆岩层沉降具有重要作用; 以及计算时上煤层未开采的假设,导致岩层的载荷与实际载荷不同, 关键层没有发生断裂现象, 预测点与工作面间关键层越多, 计算结果越小。

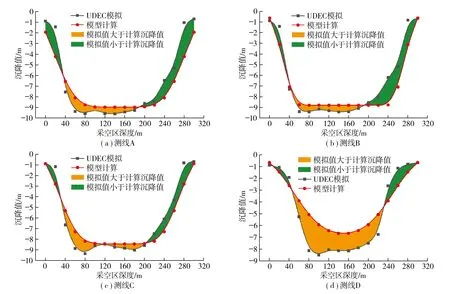
图11 双系煤层开采后上覆岩层各测线沉降值对比Fig.11 Comparison of settlement of each measuring line in the overlying strata after double-layer coal mining

双系煤层开采岩层移动模型各监测线沉降值误差统计结果见表2。由表2可知, 双系煤层开采后测线A, B, C, D上各测点有一定的误差。测线A的平均误差1.07 m, 平均误差率15.18%, 最大误差3.19 m, 该点误差率为75.41%; 测线B的平均误差0.85 m, 平均误差率12.40%, 最大误差2.56 m, 由于该点靠近一侧, 沉降值较小, 导致误差率较大, 为29.19%; 测线C的平均误差0.78 m, 平均误差率12.51%, 最大误差为1.98 m, 该点误差率为70.71%;测线D的沉降曲线趋势相似, 由于计算模型考虑了关键层的作用, 误差较大, 平均误差为1.31 m, 平均误差率为32.03%, 最大误差为3.05 m, 该点误差率为60.04%。在横向方向上, 由于模型在考虑影响半径的同时考虑了两侧悬臂梁的作用, 误差主要集中在左右两侧。在左右两侧40 m内的误差较大, 误差约为60%, 约为中间的3倍以上。而在纵向方向上, 距离开挖煤层越远, 模型计算的沉降值相对于模拟值更小, 误差也更大。上煤层上方27 m处(测线A)的平均误差率为15.18%, 而上煤层上方118 m处(测线D)的平均误差率为32.03%, 这是因为测线D位于亚关键层顶板, 而模型考虑了关键层的影响,计算的沉降值会更小。因此, 双系煤层开采模型整体误差在可接受范围内, 具有一定的适用性。

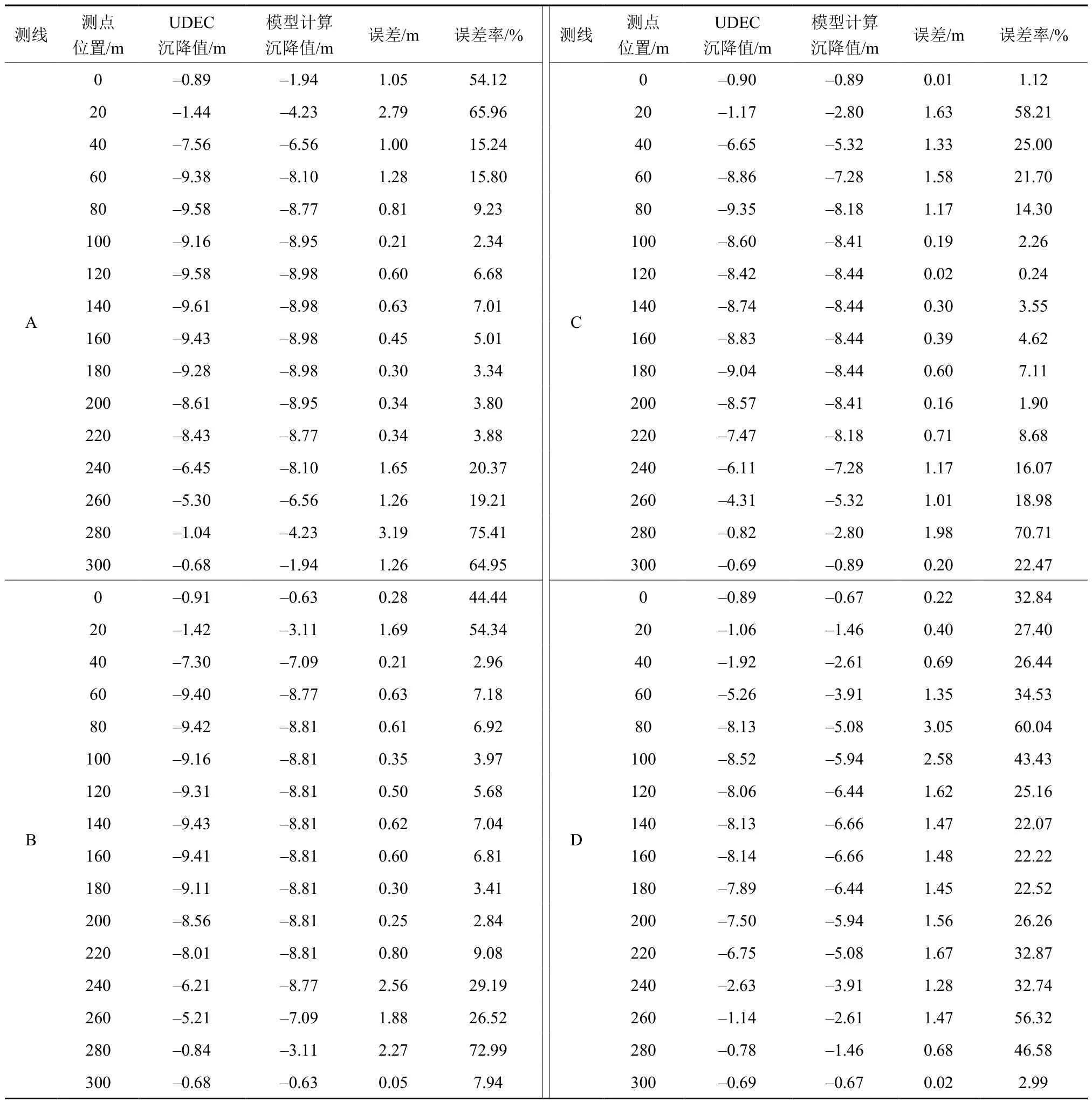
表2 双系煤层开采岩层移动模型各监测线沉降值误差统计Table 2 Statistics of settlement values errors of monitoring lines in the rock movement model of dual coal seam mining

3.3 双系煤层开采对覆岩空隙率的影响

煤炭开采后, 上覆岩层垮落形成的采空区裂隙空间是漏风和采空区气体流动的主要区域。采空区的气体流动主要受空隙率和渗透率的影响, 空隙率的分布是描述气体运移的重要参数, 同时也是描述采空区裂隙的关键指标。在建立煤岩体空隙率与全应变的关系时, 忽略煤岩体微小的本体变形和横向位移, 考虑煤岩体结构变形, 结合岩层移动模型进行分析推导[10]。根据空隙率的定义, 在初始状态下的煤岩体的空隙率为

式中,φ0为初始空隙率;kV为多孔介质孔隙的体积;zV为煤岩体的总体积。

当受采动影响时, 煤岩体在某一状态新的空隙率可表示为

式中,φ为煤岩体空隙率;tε为体积应变。

式中, ΔV为体积的变化量;V为初始体积;xε为x方向的体积应变;zε为z方向的体积应变; dU/dx为U(x,z)的一阶导数; dS/dz为S(x,z)的一阶导数。

因此, 以工作面走向为例, 工作面正中心的截面, 开采长度为300 m, 通过岩层移动模型计算得到岩层移动位移, 进而得到采动影响下上覆岩层的空隙率分布, 如图12~13所示。

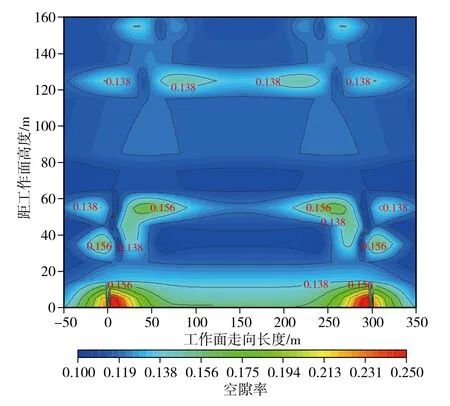
图12 上层煤开采后走向截面空隙率分布Fig.12 Distribution of void ratio in section after upper coal mining

由图12可知, 上层煤开采后, 煤层开采区域的空隙率最大, 两侧大于0.156; 采空区的中间大于0.138, 表明该区域存在较多裂隙。在关键层位置的两侧, 空隙率最大为0.156, 中间约为0.109, 这表明关键层可能没有发生断裂, 而其上方出现部分空隙率增大区域。在亚关键层区域, 空隙率较小, 岩层整体出现了移动, 没有明显的大裂隙区域, 而其上方岩层存在空隙率较大区域, 并且两岩层的厚度都相对较厚, 这表明岩层间发生了离层现象。上层煤开采后, 关键层发挥了重要作用, 20 m内的空隙率较大; 两个关键层上方局部空隙率增大, 可能出现了离层现象, 但岩层整体相对完整, 平均空隙率较小。

由图13可知, 在下层煤开采后, 煤层间岩层破坏较严重, 层间关键层与下层煤之间形成垮落带,空隙率约为0.19; 距离工作面40 m处为层间关键层的位置, 两侧的空隙率约为0.23, 裂隙区域导通到上采空区; 在层间关键层与上煤层之间, 岩层受到关键层支撑, 未发生破碎, 空隙率较小, 约为0.12;在距离工作面80 m处, 两侧空隙率为0.23, 中间位置为0.175, 由于悬臂梁的作用, 两侧岩层垮落后发生堆叠错位, 孔隙较大; 在距离工作面130 m处空隙率较大, 可能发生了离层现象。与上层煤开采相比, 双系煤层开采后空隙率增大, “活化”作用导致上覆岩层严重破碎, 平均空隙率约为0.15。随着距工作面高度的增加, 受影响区域逐渐减小, 孔隙较大的区域呈“梯形状”。根据空隙率分布图, 上下采空区之间两侧空隙率较大, 这表明下层煤工作面与上采空区和地表存在较大的裂隙, 存在导气通道, 最终导致地表漏风。

图13 下煤层开采后走向截面空隙率分布Fig.13 Distribution of void ratio in section after mining of lower coal seam

3.4 物理模型结果对比

文献[38]通过物理相似试验模拟多层煤逐层开采过程, 相似试验物理模型中上层煤开挖高度1.5 cm, 下层煤开挖高度3.5 cm, 每次开挖推进5 cm。笔者根据文献[38]中测线1的岩层移动规律,将多层煤开采岩层移动模型的计算结果与测线1进行对比, 如图14所示。由图14可知, 两条沉降曲线存在一定误差, 其中左侧误差较小, 而右侧的沉降误差较大, 平均误差为0.56 cm, 最大误差达到1 cm,平均误差率为16.7%。差异的原因是左侧岩层在开采过程中已经充分沉降, 而右侧由于岩层垮落时间较短, 沉降不够充分。测线1布置在上煤层顶板,岩层位移曲线受到推进速度影响, 因此曲线存在一定波动, 但两条曲线整体呈现相同的趋势。

图14 物理模型与模型计算结果对比Fig.14 Comparison of physical models and model calculation results

4 结 论

(1)探讨了关键层影响下“力学模型+几何方法”融合的上覆岩层移动模型的应用, 基于该成果构建了适用于双系煤层开采条件下的岩层移动模型, 并建立了岩层移动与煤层间距的关系, 推导出适用于双系煤层开采的岩层移动模型, 揭示了煤层重复开采情况下岩层二次扰动、“活化”后的移动变形规律, 弥补了原模型只能预测单层煤开采的不足。

(2)运用UDEC软件对双系煤层开采进行数值模拟, 对比了两次开采后的岩层位移曲线。上煤层开采后的曲线误差较小, 重合度较高; 在下煤层开采后, 测线A, B, C处的岩层沉降值与沉降模型计算值相比误差较小, 误差率小于15.18%, 沉降曲线呈现较好的一致性和相似趋势, 验证了双系煤层开采岩层移动模型的适用性。与文献[38]中物理相似模型开挖后结果对比, 平均误差率为16.7%, 两条曲线整体呈现相同的趋势。

(3)分析了双系煤层开采后的空隙率分布, 与单层煤开采相比, 空隙率发生了明显变化, 双系煤层开采对上覆岩层造成更严重的破坏, 增加了采空区贯通的可能, 进而产生导气通道。随着距工作面高度的增加, 受影响区域逐渐减小, 孔隙较大的区域呈“梯形状”。根据空隙率分布图, 上下采空区的两侧存在裂隙通道, 可能与地表和上采空区存在较大的裂隙通道有关, 最终导致地表漏风。