动荷载作用下不同应力波透射性结构面围岩层裂特性

朱建波, 毕 硕, 孙家鑫, 暴伟越, 廖志毅, 王 钥

(1.天津大学 水利工程仿真与安全国家重点实验室, 天津 300350; 2.深圳大学 广东省深地科学与地热能开发利用重点实验室, 广东 深圳 518060; 3.深圳大学 深地科学与绿色能源研究院, 广东 深圳 518060; 4.大连理工大学 岩石破裂与失稳研究所, 辽宁 大连 116081)

煤矿巷道经常受到矿震、爆破、机械振动等动荷载的影响[1–3],动荷载以应力波的形式在巷道围岩内传播, 当应力波传播至巷道表面时, 产生反射现象, 由入射波与反射波叠加产生的拉伸应力波会使巷道表面围岩产生层裂破坏[4–5]。同时, 结构面也会使围岩内应力波产生透射和反射, 结构面的拉伸力学特性在层裂破坏中也起着重要作用[6], 因此煤矿巷道的动力响应颇为复杂[7]。

在复杂的地质活动下, 围岩内会形成波阻抗与岩体相近的结构面, 这类结构面节理刚度和密度较高, 可以近似认为在应力波穿过这类结构面时完全透射[8–9], 笔者将此类结构面定义为“高应力波透射性结构面”, 将应力波无法完全透射的结构面定义为“低应力波透射性结构面”。含高应力波透射性结构面围岩由于高应力波透射性结构面特殊的无反射特性使其力学响应不同于含低应力波透射性结构面围岩, 在破坏模式上也表现出显著的差异性。因此, 开展动力扰动作用下的含高应力波透射性结构面围岩破坏特征研究对维护煤矿巷道的稳定性具有重要意义。

目前, 动荷载作用下含结构面岩体的动力响应及围岩层裂特性研究, 主要集中在理论研究、试验研究和数值模拟研究等3个方面。理论研究方面,李夕兵等[10]对半正弦波入射下岩石自由面附近发生的入射波、反射波相互作用进行了理论推导, 分析了岩石层裂破坏特性; 占学军等[11]分析了矩形、三角形和指数衰减三角形脉冲荷载下的层裂现象,并对层裂厚度进行了理论推导; ZHU等[12–13]研究了应力波入射含黏弹性节理面、断续节理面岩体的动态响应特性, 并推导出了相关的解析解。

现有试验研究主要集中于利用霍普金森压杆(SHPB)装置对含缺陷岩体和混凝土试样展开的冲击破坏试验。卞梁等[14]基于SHPB试验装置研究了损伤和应变率对混凝土层裂强度的影响, 发现层裂强度具有明显的应变率效应; 邱加冬等[15]利用SHPB装置分别对有无预制缺陷的花岗岩试样进行了层裂破坏特性的研究, 研究结果表明预制缺陷会影响初始层裂破坏位置, 且反射拉伸波上升沿越长时, 初始层裂破坏越可能出现在预制缺陷处; TAO等[16]使用SHPB装置研究了含预制孔洞岩样的动态拉伸破坏过程, 过程中圆孔周围产生应力集中现象, 研究发现岩样破坏是静应力集中和动应力集中共同作用的结果。目前, 关于岩体试验的研究大多针对完整、含孔洞或含预制缺陷岩体受动力荷载作用下的破坏特征, 鲜有关于含结构面围岩破坏模式的研究。

由于受试验材料制备的限制, 国内外学者利用数值模拟软件开展了岩体受荷破坏的研究。左宇军等[17]通过基于细观损伤力学开发的RFPA2D分析系统, 研究了不同自由面情况下冲击载荷对岩石层裂过程的影响; 张晓春[18]、卢爱红等[19]通过数值模拟的方法研究了动力扰动作用下, 应力波强度、巷道埋深和岩体物理性质等因素对围岩层裂特性的影响; TAO等[20]对含有椭圆形孔洞的地下硐室围岩进行了一维简化, 研究了硐室在动态荷载下的层裂破坏过程; 廖志毅等[21]采用数值模拟方法模拟了动荷载扰动下含结构面的地下硐室, 研究了结构面对于地下硐室层裂破坏和应力波传播的影响; NIU等[22]对不同频率和不同幅值下的1/4半正弦应力波作用在不同长度青砂岩杆的层裂破坏进行了模拟研究; XU[23], ZHAO等[24]通过模拟的方法分别研究了混凝土、砂岩为硐室材料时, 硐室围岩在不同结构条件和不同荷载类型下的层裂破坏情况; WANG等[25]通过自定义子程序的方法将岩石的连续损伤本构模型引入数值模拟软件模拟了动荷载作用下岩石的层裂过程。上述研究多集中于完整围岩或含低应力波透射性结构面围岩在动力扰动作用下岩体性质以及动荷载参数对围岩层裂破坏特征的影响, 鲜有含高应力波透射性结构面围岩层裂破坏特征的相关研究, 难以满足工程问题的需要。

因此, 笔者围绕动荷载扰动下, 含高、低应力波透射性结构面巷道围岩层裂破坏这一科学问题,分别开展了含有不同抗拉强度的低应力波透射性结构面围岩试样室内动载试验、和含高应力波透射性结构面围岩层裂破坏数值模拟试验。基于ABAUQS/Explicit, 建立了动载扰动下含Cohesive单元的低应力波透射性结构面围岩层裂破坏的数值模型, 对模拟结果和室内试验结果进行对比, 验证了数值模型的准确性。在此基础上, 建立含高应力波透射性结构面的数值模型, 分析应力波作用下结构面位置、结构面抗拉强度和应力波幅值对巷道围岩层裂破坏特征的影响规律。研究成果可为煤矿巷道支护设计和稳定性评价提供参考。

1 试验方案设计

试验主要研究受动荷载扰动下含结构面围岩的层裂破坏规律。试验材料选用均质性较好、地下工程常见的青砂岩, 产自四川省内江市隆昌市,材料物理参数见表1。

表1 试验材料及其基本物理参数Table 1 Test materials and basic parameters

青砂岩试样材质较均匀、无明显层理, 为长方体杆件, 其杆径为35 mm×35 mm, 长度为1 000 mm,如图1所示。试样两个端面需要经过垂直打磨, 使两端面的不平行度和不垂直度均小于0.02 mm。同时, 将两个端面的光滑程度控制在一定范围内, 以此来减小入射杆/透射杆和岩石试样之间的摩擦力,从而避免试样横向的不均匀形变。距离加载段每隔200 mm布置一个测点, 共布置4个测点, 如图1所示。

图1 试验试样Fig.1 Test specimens

因含高应力波透射性结构面围岩制备难度较大, 室内试验研究对象只限低应力波透射性结构面围岩, 并将试验结果作为数值模型验证的依据。实际工程中常用工程胶、云石胶等作为围岩加固材料, 围岩加固后也会形成类结构面的结构, 因此针对结构面不同抗拉强度的研究条件, 笔者选取具有黏性的石膏、云石胶和工程胶作为岩体中不同抗拉强度的结构面材料。

软弱结构面位置位于长方体试样正中心处, 结构面的制备过程为: 首先将左右两根岩石杆端部进行打磨, 使其平整度满足规范要求; 然后将两根岩石杆放置于水平平台之上, 调整两杆的水平位置和前后相对位置使其处于同一直线上, 预留3 mm间隙用于浇筑结构面材料; 固定好两杆的位置后, 使用纳米胶带将其四周紧密缠绕, 并对岩石边角处施加一定的力使纳米胶带与岩石之间紧密接触, 防止浇筑过程中结构面材料在凝固之前从缝隙流出, 如图2(a)所示; 由纳米胶带顶部预留的孔隙中浇筑结构面材料, 并在浇筑过程中用干净的细铁丝对其进行持续搅拌, 保证结构面材料的凝结过程中不产生气泡从而影响其均质性; 当结构面材料从预留孔隙中流出时, 停止浇筑; 待结构面材料终凝后(1 h),拆除纳米胶带, 并用砂纸打磨结构面至平整后备用, 最终结构面效果如图2(b)所示。不同结构面材质的抗拉强度通过室内巴西劈裂试验测得, 试样制备如图2(c)所示。

图2 结构面制备示意Fig.2 Schematic diagram of structural surface preparation

试验装置为分离式霍普金森压杆, 试验装置如图3所示。其中入射杆为圆柱型硅锰钢杆, 杆径为50 mm, 长度为3 000 mm。入射子弹为同材质的圆柱型钢锭, 直径为50 mm, 长度为100 mm。钢杆的弹性模量为211 GPa, 密度为7 652 kg/m3, 纵波波速为5 201 m/s。试验中采用直径为13 mm, 厚度为1.5 mm的黄铜圆片作为波形整形器, 用于消除应力波的弥散效应。

2 不同结构面抗拉强度影响规律

结构面的不同组分使其整体力学性能和界面两端黏结性能产生较大差异。笔者通过界面无填充、石膏填充、云石胶填充和工程胶填充等4种工况来说明结构面抗拉强度的变化。结构面的抗拉强度通过室内巴西劈裂试验测得, 分别测得石膏、云石胶和工程胶作为填充材料时圆盘试样的巴西劈裂强度σK为3.0, 4.9, 6.8 MPa。可知工程胶充填结构面的抗拉强度明显高于石膏和云石胶填充。

完整砂岩杆及不同结构面强度砂岩杆的层裂破坏试验结果如图4所示, 应力波从长方体试样右端进入, 结构面均距离自由端500 mm, 位于长方体试样中心处。

图4 不同结构面抗拉强度时岩石杆破坏结果Fig.4 Failure results of rock rods with different tensile strengths of structural planes

当结构面材质为无填充、石膏和云石胶填充时, 砂岩杆在应力波的作用下, 杆件中部的结构面先发生破坏, 随后靠近自由端处的岩石发生层裂破坏。由于结构面处强度较低, 在经历第1段轴向压缩波时, 结构面界面先发生破坏, 随后砂岩杆自由端发生拉伸破坏。当使用力学性能较好的工程胶填充结构面时, 结构面在相同峰值的第1段压缩波作用下未发生破坏, 仅靠近自由端处的岩石发生层裂破坏。

对试验结果中的结构面抗拉强度、层裂体长度(自由端到发生层裂破坏位置的长度)和4号测点拉伸应力幅值进行总结, 绘制3者的变化趋势图,如图5所示。由图5可知, 相较于无充填结构面, 当结构面材质为石膏时, 结构面抗拉强度提高至3 MPa, 测点拉伸应力提高了1.9%, 层裂体长度缩短了16.0%; 当结构面材质为云石胶时, 结构面抗拉强度提高至4.9 MPa, 拉伸应力提高了15.0%, 层裂体长度缩短了31.4%; 应力波幅值相同时, 结构面先发生破坏。随着结构面抗拉伸强度的增加, 靠近自由端处4号测点拉伸应力逐渐增加, 层裂体长度逐渐缩短。当工程胶填充结构面时, 结构面抗拉强度提高至6.8 MPa, 结构面不发生破坏, 4号测点拉伸应力处于较高水平, 层裂体长度为16.4 cm。

图5 应力波幅值、层裂体长度与不同结构面抗拉强度关系Fig.5 Relationship between stress wave amplitude, spall thickness and tensile strength of different structural planes

3 数值模拟

工程模拟有限元软件ABAQUS/Explicit在处理非线性动力学问题时能够详细展现破坏过程, 精确反映材料破坏前的应力–应变状态, 且其内置的Cohesive单元可以用来模拟两个单元之间的黏合行为、不同种材料之间的界面黏结行为和界面的完整性等。笔者通过在围岩模型中批量插入Cohesive单元对含高应力透射性巷道围岩在动荷载影响下的拉伸破坏行为进行模拟。

利用分离式霍普金森压杆装置和ABAQUS/Explicit软件研究岩石受动荷载影响下的动态响应破坏过程。

3.1 数值模型建立

基于ABAQUS有限元软件, 建立动力扰动作用下岩石层裂破坏的数值模拟模型, 设置模型左侧为加载端, 右侧为自由端。鉴于笔者侧重于探究一维应力波作用下岩石的层裂破坏过程, 为增加计算效率, 将模型简化为二维平面结构, 模型尺寸为35.3 mm×1 000 mm, 单元数3 946个。

建立含低应力波透射性结构面的围岩模型, 需分3部分进行建模, 分别为两段500 mm的围岩模型与一段3 mm的结构面模型, 并分别设置两段围岩与结构面之间的接触方式。面与面之间的接触考虑采用通用接触(General Contact), 对于围岩与结构面之间的接触, 考虑到其易发生受拉破坏, 在接触属性中添加了Cohesive单元行为以及损伤演化准则。

完整巷道围岩和含结构面围岩数值模型如图6(a), (b)所示, 与验证试验模型保持一致, 围岩材料和结构面材料参数及Cohesive参数设定见表2。

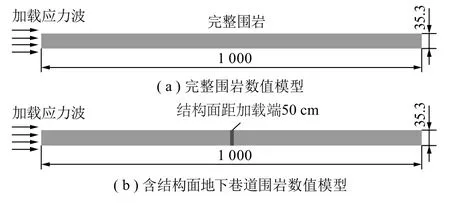
图6 数值模型示意Fig.6 Schematic diagram of numerical model

表2 Cohesive单元基本参数设定Table 2 Basic parameter setting of Cohesive unit

3.2 对比验证

根据上述过程建立基于分离式霍普金森压杆装置的二维围岩数值模型进行数值模拟仿真, 通过对比完整围岩和含结构面围岩的破坏过程和应力波幅值等参数验证数值模型的可行性。

在进行模型验证时, 岩样加载端处的入射波形特征与室内试验保持一致, 波形如图7所示。通过对完整围岩和低透射性结构面围岩数值和物理试验结果的对比, 验证模拟试验围岩材料参数和结构面材料参数、Cohesive单元参数的准确性。

图7 加载应力波波形Fig.7 Waveform diagram of loading stress wave

3.2.1 完整围岩验证

笔者首先通过对比完整围岩的数值模拟结果,对数值模型和围岩材料设置的有效性和准确性进行验证。选取试验过程中围岩的4号测点(距自由端200 mm处)与数值模型中相同位置拉伸应力波进行比较, 以此验证数值模型层裂破坏过程和模型参数设置的合理性和准确性。两者的层裂破坏结果和4号测点拉伸应力波对比结果如图8所示。

图8 完整巷道围岩动力学试验与数值模拟结果Fig.8 Dynamic test and numerical simulation results of surrounding rock of complete tunnel

3.2.2 含低应力波透射性结构面围岩验证

在验证完整围岩模型参数合理的基础上, 通过对比含低应力波透射型结构面模型模拟破坏过程,验证结构面参数设置的合理性。选取石膏填充材料作为含低应力波透射型模型中结构面材料对比分析, 结构面位置与试验保持一致, 位于杆件中心处, 同样选取距自由端200 mm处4号测点的应力波对比分析, 室内试验和模拟结果如图9所示。

图9 含结构面巷道围岩动力学室内试验和数值模拟结果Fig.9 Dynamic test and numerical simulation results of surrounding rock of cavern with structural plane

由图9可知, 含低应力波透射性结构面围岩在室内试验时发生层裂破坏的位置与在数值模拟时相同, 均距离自由端22 cm。由图9(c)可知, 室内与模拟试验在4号测点拉伸应力波幅值误差在15%以内, 波形变化趋势大致相同, 故可以认为含低应力波透射型结构面模型与室内试验具有较高的一致性, 结构面参数设置合理。

4 高应力波透射性围岩层裂特性数值模拟

第3节验证了数值模型的可行性, 围岩材料参数、结构面材料参数和Cohesive单元参数设置的准确性, 在此基础上, 笔者重点研究不同工况下含高应力波透射性结构面围岩的破坏过程及力学特征。

建立含高应力波透射性结构面围岩数值模型时, 以在完整1 000 mm围岩的既定位置插入Cohesive单元来实现对高应力波透射性结构面的模拟。

4.1 结构面抗拉强度对层裂的影响

由室内试验结果可知, 结构面抗拉强度对含低应力波透射型围岩受力状态及层裂位置影响较大, 因此针对含高应力波透射型结构面, 进行相同入射波幅值下的含不同抗拉强度结构面的模拟试验。

为详细研究含不同抗拉强度结构面围岩在动力扰动下的破坏形式与层裂破坏过程, 分别将结构面抗拉强度设置为5, 10, 15, 20, 25 MPa进行研究,结构面位置位于杆件正中心处, 通过调整Cohesive单元的黏聚力参数实现对结构面抗拉强度的调整。加载应力波幅值为75 MPa, 波长为1 000 mm。对不同结构面抗拉强度条件下的含高应力波透射性结构面围岩的破坏过程进行模拟, 并对A, B两点(A, B测点为紧邻围岩层裂破坏面及结构面的两个测点, 位置如图10(a)所示)的波形进行了监测, 其监测到的应力波幅值如图11所示。

图10 不同结构面强度数值模拟相关计算结果Fig.10 Numerical simulation related calculation diagram

图11 不同结构面抗拉强度巷道围岩A, B测点处拉伸应力波幅值曲线Fig.11 Tensile stress amplitude curves at A and B measuring points of surrounding rock of caverns with different structural plane tensile strength

数值模拟结果得出, 在应力波的扰动下, 当结构面抗拉强度为5, 10, 15, 20 MPa时, 含高应力波透射性结构面围岩在岩石靠近自由端处和结构面处均发生破坏; 当结构面抗拉强度为25 MPa时, 只在靠近自由端处发生层裂破坏, 结构面处未发生破坏。当冲击应力波在巷道围岩模型中传播时, 其材质自身的密度、孔隙率和阻尼等物理性质及弹性模量等力学性质会影响应力波的传播, 应力波幅值会随着传播距离的增加逐渐衰减。当结构面处拉伸应力波叠加后的幅值大于结构面抗拉强度时, 结构面发生破坏, 反之幅值小于结构面抗拉强度结构面不发生破坏。由图10(b)可知, 不同高应力波透射性结构面抗拉强度下的围岩层裂拉伸破坏位置相同, 且与图9中完整围岩的破坏位置一致, 均在距自由端260 mm处发生破坏, 不同于低应力波透射性结构面围岩层裂规律(图4)。这是由于相同应力波的作用下, 高应力波透射性结构面的透射系数几乎等于1, 不会在结构面处产生反射拉伸应力波。因此, 该类型结构面抗拉强度不影响围岩层裂的破坏位置, 应力波先后在靠近自由端处发生反射波叠加现象, 最终围岩先发生层裂破坏, 然后结构面发生拉伸破坏。

由图11可知, 靠近层裂位置的测点A处应力波幅值随着结构面抗拉强度的增加基本保持水平, 表现出结构面抗拉强度无关性; 靠近结构面位置测点B处的应力波幅值随着结构面抗拉强度的增加而增加。根据最大拉应力破坏准则, 当结构面和围岩处发生层裂破坏时, A, B测点处测得的拉伸应力波幅值分别小于围岩层裂破坏处和结构面处的应力波幅值, 考虑为破坏后的残余拉伸应力波。当结构面抗拉强度为25 MPa时, 由于到达结构面部位的拉伸应力波幅值经衰减后低于25 MPa, 未达到结构面破坏要求, 所以未发生破坏。因此, 测点A的拉伸应力波幅值表现出结构面抗拉强度无关性, 测点B的拉伸应力波幅值与结构面是否破坏有关: 当结构面发生破坏时, 与结构面抗拉强度成正相关; 当结构面未发生破坏时, 测点B的拉伸应力波幅值趋向于低于结构面抗拉强度的定值。

4.2 不同应力波对层裂的影响

应力波幅值对含结构面围岩层裂的破坏程度和破坏规律影响较大。为研究不同应力波幅值下含高应力波透射性结构面围岩的动力学响应, 分别将应力波幅值设置为45, 55, 65, 75和85 MPa, 应力波的波长固定为1 000 mm。将结构面的抗拉强度设定为20 MPa, 结构面位置仍位于杆件正中心处。

对不同幅值应力波作用下的含高应力波透射性结构面围岩破坏过程进行模拟, 并对A, B两点(A, B测点为分别紧邻围岩层裂破坏面及结构面的两个测点, 位置同图10(a)所示)的应力波波形进行监测。

不同幅值应力波条件下的数值模拟结果如图12所示。由图12可知, 随着应力波幅值的改变, 巷道围岩整体出现: 整体未破坏(应力波幅值45 MPa),围岩完整–结构面破坏(应力波幅值55, 65 MPa), 围岩破坏–结构面破坏(应力波幅值75, 85 MPa)等3种破坏形式。

图12 不同幅值应力波数值模拟计算结果Fig.12 Numerical simulation calculation results of different stress amptitudes

通过模拟结果可知, 应力波在高透射性结构面未发生反射现象, 应力波在340 μs时到达结构面,在750 μs时到达自由端并发生反射。巷道围岩中的应力波随着传播距离的增加逐渐衰减, 当应力波幅值为45 MPa时, 从自由面反射的应力波在整个围岩和结构面位置处的幅值未满足拉伸破坏强度要求,故未发生破坏。随着应力波幅值的增加, 由于结构面的抗拉强度低于围岩的抗拉强度, 整体在破坏时依次出现围岩完整–结构面破坏, 围岩破坏–结构面破坏(围岩先破坏, 结构面后破坏)的破坏模式。当应力波幅值增大到85 MPa时, 靠近自由面的围岩在高幅值反射应力波的叠加作用下多处发生层裂破坏, 同时高幅值反射波传播至结构面致使结构面也发生拉伸破坏。

由图13可知, 随着入射应力波幅值的增大, 在自由端反射形成的反射拉伸波幅值也随之增大。

图13 不同幅值应力波下巷道围岩A, B测点处拉伸应力波曲线Fig.13 Tensile stress amplitude curves at measuring points A and B of surrounding rock under different stress amplitudes

对靠近自由端测点A来说, 当入射波应力低于75 MPa时, 围岩未发生层裂破坏, A点测得的幅值随着入射波幅值的增加呈上升趋势。当入射波应力高于75 MPa时, 围岩发生破坏, A点测得的幅值稳定在26 MPa左右。靠近结构面测点B展现出相同的变化规律, 当入射波幅值低于55 MPa时曲线成正比, 高于55 MPa时, 结构面发生破坏, 幅值稳定在19 MPa左右。根据最大拉应力破坏准则, 测点前位置发生破坏时, 测得的拉伸应力波为此位置发生拉伸破坏后的残余拉伸波, 其最大拉伸应力幅值约等于围岩的层裂强度, 因此破坏位置后测得的幅值基本保持不变。由上述分析可知, 当测点前位置处未发生破坏时, 测点测得的应力波幅值随着入射波幅值的增加而增加。反之测点前位置处发生破坏时,测点测得的应力波幅值趋于一个低于监测位置处层裂强度的定值。

4.3 结构面位置对层裂的影响

巷道围岩中的结构面控制着围岩整体的破坏情况, 结构面距离自由端的位置也对围岩整体的力学响应起着关键作用。

为详细研究结构面的不同空间位置对于围岩层裂破坏的影响规律, 分别将结构面位置设置为距自由端167, 334, 500, 667 mm和833 mm。结构面抗拉强度设置为20 MPa, 应力波幅值设置为75 MPa,波长1 000 mm。

不同结构面位置下围岩数值模型层裂破坏形式及破坏位置如图14所示。

图14 不同结构面位置时巷道围岩动力学数值模拟结果(左侧为加载端, 右侧为自由端)Fig.14 Numerical simulation results of surrounding rock dynamics of cavern at different structural plane positions(the left side is the loading end, and the right side is the free end)

当高应力波透射性结构面距离自由端较远(833, 667, 500 mm)时, 围岩先发生层裂破坏, 且其围岩层裂破坏位置与不含结构面围岩发生层裂破坏位置基本一致(距自由端260 mm), 随后结构面处发生拉伸破坏。当高应力波透射性的结构面距离自由端较近(167, 334 mm)时, 围岩只发生结构面处的拉伸破坏, 未发生层裂破坏。

结合距离自由端200 mm和160 mm处的应力波波形(图15), 对结构面与自由端之间的围岩进行分析, 定义第1个反射拉伸波的完整脉宽所持续的时长为有效波长, 发现当结构面距离自由端的距离缩短时, 反射拉伸波的有效波长也会随之缩短(结构面距自由端334 mm和167 mm时, 有效波长分别为0.475, 0.195 m), 拉伸波的幅值也会降低。这是因为当结构面距离自由端较近时, 反射拉伸波抵达结构面时首先发生了拉伸破坏, 破坏后的结构面会形成新的自由面, 自由面的存在会使刚刚抵达的反射拉伸应力波发生二次反射, 成为向自由端传播的压缩应力波。结构面与自由端越近, 形成的新自由面距离巷道壁就越近, 导致多次反射并相互叠加。拉伸应力波的有效波长缩短、幅值降低, 无法达到围岩层裂所需的最大拉应力(26.7 MPa), 故结构面距离自由端较近(334, 167 mm)的情况下围岩不会发生层裂破坏。

图15 不同位置处的应力波波形Fig.15 Stress wave waveforms at different positions

5 讨 论

现有围岩层裂研究主要针对完整围岩, 通过分析层裂破坏特征指导工程支护问题[27–28], 对于含结构面围岩的研究较少, 尤其是缺乏对含高应力波透射性结构面围岩的层裂破坏特征研究。笔者通过数值模型开展了对含高应力波透射性结构面围岩层裂破坏研究, 分别讨论了结构面位置、结构面抗拉强度等因素对层裂破坏特征的影响, 研究结果可为含不同结构面类型的围岩破坏情况进行预测, 为支护工程提供依据。

通过笔者的室内试验和数值模拟结果发现, 当结构面抗拉强度改变时, 含低应力波透射性结构面与高应力波透射性结构面围岩的破坏模式不同, 不同抗拉强度下结构面的层裂体长度和围岩层裂位置后的应力波幅值(4号测点和A测点)对比如图16所示。

图16 高、低应力波透射性结构面对比Fig.16 Comparison of high and low stress wave transmission structural planes

由图16可知, 低应力波透射性的试验中, 破坏模式为结构面先发生破坏, 后围岩发生层裂破坏。当结构面发生破坏时, 随着结构面抗拉强度的增大, 层裂体长度逐渐缩短, 测点处的应力波幅值也逐渐增大。高应力波透射性的数值模拟中, 破坏模式为围岩先发生层裂破坏, 后结构面发生破坏, 层裂体长度和测点处应力波幅值表现出结构面抗拉强度无关性。

破坏行为不同的原因在于结构面的透反射系数。室内试验中, 当结构面抗拉强度不同时, 透反射系数并不一致, 结构面强度的增加导致透射系数的增加, 进而自由端处应力波幅值增加, 应力波叠加强度更快到达围岩破坏强度, 导致层裂体长度逐渐缩短。

反观数值模拟中, 结构面为高应力波透射性,应力波全部透射, 即透射系数等于1。应力波经过结构面时不发生衰减, 层裂体长度及自由端应力波幅值不受到抗拉强度改变的影响, 抗拉强度改变仅影响到结构面破坏与否。笔者在进行数值模拟时,设置围岩材质为理想均质材料, 且未考虑温度、湿度等环境因素的影响, 存在一定局限性, 后续可开展更接近实际工况的试验研究。

6 结 论

(1)结构面抗拉强度显著影响低应力波透射性结构面围岩的破坏特征, 对高应力波透射性结构面围岩破坏特征无明显影响。随着结构面抗拉强度的增加, 低应力波透射性结构面围岩层裂体长度逐渐缩短, 结构面拉伸破坏先于围岩层裂破坏; 高应力波透射性结构面的层裂体长度则与结构面抗拉强度无关, 围岩层裂破坏先于结构面拉伸破坏。

(2)应力波幅值是影响巷道围岩破坏模式的重要因素。随着应力波幅值的增加, 高应力波透射性结构面围岩破坏模式依次为: 整体未破坏、围岩完整–结构面拉伸破坏、围岩层裂破坏–结构面拉伸破坏。

(3)结构面位置对高应力波透射性结构面巷道围岩的层裂破坏特征影响较为显著。结构面距离自由端较远时, 围岩先发生层裂破坏再发生结构面拉伸破坏, 结构面位置不影响层裂位置; 结构面距离自由端较近时, 巷道围岩只发生结构面拉伸破坏, 不发生层裂破坏。