天然裂缝多特征组合对页岩储层渗流的影响

刘建锋, 何 鑫, 薛福军, 代晶晶, 杨建雄, 黄浩勇, 侯正猛

(1.四川大学 水利水电学院, 四川 成都 610065; 2.中国石油天然气股份有限公司西南油气田分公司 页岩气研究院, 四川 成都 610051; 3.四川大学 中德能源研究中心, 四川 成都 610065)

页岩气作为一种清洁的非常规油气资源, 在全球非常规油气的开发进程中, 占据着重要地位。近年来, 北美页岩气的商业化开采使得世界能源格局发生变化[1–3], 我国的页岩气勘探开发也处于迅速发展阶段。在当前的页岩气开采实践中, 常采用水力压裂技术来刺激储层裂缝[4–6], 从而形成水力压裂区域与天然裂缝共同组成的改造储层体积, 即Stimulate Reservoir Volume (SRV), 从而达到有效开采页岩气的目的。地质勘探调查发现, 页岩储层内存在丰富的天然裂缝[7–9], 其对储层渗透性有着不可忽视的影响[10]。通常情况下, 裂缝网络的发育程度越高, 储层的渗透性就越高, 储层的开发效果也越佳[11–14], 而不同的天然裂缝特征, 会对储层的渗透性产生较大影响, 从而影响页岩储层渗流行为及产气量。因此, 综合考虑多种天然裂缝特征对储层渗透性的影响, 对于页岩气的开发利用具有重要意义。

近年来, 国内外学者在天然裂缝特征对储层渗流行为的影响方面进行了诸多研究。李玉梅等[15]基于渗流–应力耦合数值算法, 分析了压裂裂缝长度、天然裂缝角度等因素对储层渗流的影响; 赵猛等[16]基于天然裂缝网络模型, 探究了天然裂缝间距、簇数、渗透率等裂缝特征对储层渗流的影响,并对不同特征的影响大小进行了排序; 杜旭林等[17]基于嵌入式离散裂缝模型, 并考虑了裂缝的闭合作用, 以此研究了天然裂缝宽度特征对储层渗流的影响; 慎国强等[18]基于流固耦合作用下的双重介质渗流理论, 分析了天然裂缝长度、倾斜角以及连通性对储层渗流的影响; 张志伟等[19]通过建立等效裂缝渗流模型, 探究了裂缝长度、宽度、渗透率对储层渗流量的影响。虽然已有研究在天然裂缝特征影响储层渗流方面已有较多具有指导意义的成果, 但以上成果尚未充分探讨不同天然裂缝特征组合对储层渗流行为的影响, 且鲜少涉及对于天然裂缝密集度特征的研究, 会影响页岩气藏水力压裂施工方案设计、产量评估等。为解决以上问题, 笔者从天然裂缝的多种特征着手, 系统探究了天然裂缝特征组合变化对储层渗流的综合影响。

数值模拟在页岩气的开发研究中具有十分重要的意义, 通过数值模拟的方式, 能够较为准确地模拟页岩储层内页岩气的赋存状态、天然裂缝分布特征及缝网形态等, 从而对储层产量进行有效地分析评估, 这种方法使得研究者能够更好地了解页岩气开采的相关条件, 为提高页岩储层产量提供有益参考[14,20–23]。COMSOL Multiphysics为一种基于有限元方法的数值模拟软件, 具有很强的多物理场耦合计算能力, 包含广泛的物理库和多模块功能,可自定义偏微分方程, 支持并行计算, 对于解决多场耦合下的基质–缝网渗流问题有着很高的适用性。

笔者基于COMSOL软件对特定页岩储层进行了数值模拟, 旨在研究不同天然裂缝特征组合对储层渗流的影响规律, 以期通过该研究对页岩储层压裂施工方案设计、产量提升提供参考。

1 数学模型

在页岩气的开采过程中, 孔隙压力的变化会导致储层产生变形, 使得储层的渗流参数发生改变,从而影响储层的渗流量, 且储层中的气体流动又包括了基质中的气体扩散以及缝网中的气体渗流, 故而笔者基于此建立数学模型。

1.1 渗流场方程

页岩气在储层中主要以吸附气和游离气的形式存在, 其渗流形式可分为在岩石基质孔隙中的扩散以及在裂缝中的流动。在基质系统中, 页岩气的扩散可以通过达西定律进行描述, 页岩气的吸附特性可以通过朗格缪尔的吸附方程来考虑, 结合小变形原理及质量守恒, 整理后可得到基质系统内的渗流方程:

式中,φm为基质的孔隙度;km为基质渗透率,10–3μm2;μg为气体黏度, Pa·s;αm为比奥系数;Vε为体积应变;ρg为气体密度, kg/m3;M为气体摩尔质量, kg/mol;R为普适气体常数, J/(mol·K);T为温度, K;LV为朗格缪尔体积常数, m3/kg;PL为朗格缪尔压力常数, Pa;ρs为基质密度, kg/m3;ρgst为常态下的气体密度, kg/m³;pmg为基质内的气体压力, Pa。

在裂缝系统中, 水力裂缝和天然裂缝是页岩气流动的主要通道, 可用达西定律结合质量守恒定律描述其流动, 裂缝内的渗流方程可以表示为

式中,kf为裂缝渗透率, 10–3μm2;pfg为裂缝内的气体压力, Pa;ω为裂缝张开度, 指裂缝面在法向上的位移, m。

1.2 变形场方程

在页岩储层系统中, 变形场方程会受到孔隙压力的影响[24–27], 忽略惯性力和黏性力的作用, 根据Biot理论, 其平衡方程为

式中,σ为总应力, Pa;g为重力加速度, m/s2。

根据岩体小变形假设, 储层内岩石基质的应力–应变关系可以表示为

式中,σ′为基质的有效应力, Pa;C为弹性刚度张量;ε为应变张量;I为单位张量。

将式(4), (5)代入式(3), 可得:

式中,u为位移分量。

为了表述储层内裂缝面的应力–应变关系, 引入式(7)[28–30]。

式中,σf′为裂缝面有效应力, Pa;T为裂缝面刚度矩阵。

裂缝面不连续处加载的自然边界条件可表示为

式中,n为裂缝表面的单位向量。

2 模型验证

2.1 DFM方法验证

为了验证该数学模型的准确性, 通过引入离散裂缝模型DFM(Discrete Fracture Model)进行数值模拟, 将其结果与扩展有限元法XFEM(Extended Finite Element Method)及扩展有限体积法XFVM (Extended Finite Volume Method)的结果[31]进行对比,以此来验证模型的正确性。

离散裂缝模型的网格如图1所示。

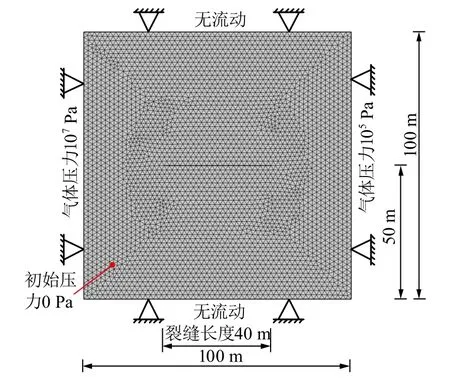
图1 DFM网格及边界条件Fig.1 DFM Mesh and boundary conditions

包含6 850个域单元和224个边界单元, 模型高宽均为100 m, 采用自由三角形网格划分, 模型正中央有一水平裂缝, 长度为40 m。模型左、右边界上的压力分别为1×107Pa与1×105Pa, 上、下两侧采用无流动边界条件, 模型区域内初始压力为0。四周均采用固定约束边界条件。模拟使用的数据见表1。

表1 数值模拟的主要参数Table 1 Main parameters for numerical simulation

使用COMSOL软件引入上述数学模型, 并对DFM模型进行数值模拟, 得到流体压力分布, 如图2所示。

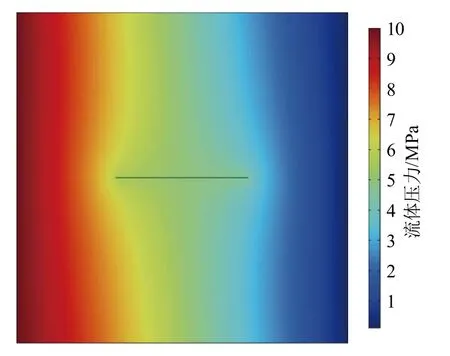
图2 流体压力分布Fig.2 Fluid pressure distribution

由图2可以明显地看出, 由于边界条件压力差的缘故, 基质部分表现出明显的压力梯度; 裂缝部分, 由于裂缝的渗透率相对于基质更大, 因此裂缝内部的流动速度更快, 表现出沿着裂缝方向的优势流动, 这说明数值模拟结果与实际情况相吻合。图3为x及y方向上的位移场分布情况, 由图3可知, 位移场分布大致沿裂缝对称, 从y方向上的位移场分布可见, 裂缝上表面有着向下的位移趋势, 裂缝下表面有着向上的位移趋势, 因此得到由于裂缝内外压力差的缘故, 裂缝表现为趋向于闭合的趋势。

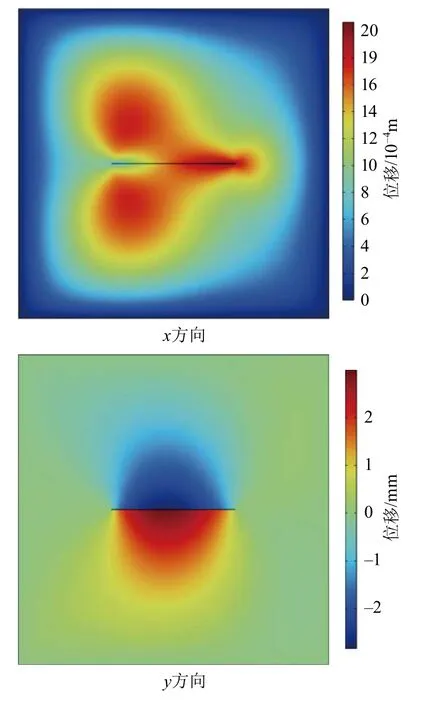
图3 x, y方向位移场云图Fig.3 Displacement field maps in x, y directions

为了将不同裂缝位置的数值模拟结果与已有文献结果进行对比, 读取裂缝上距离裂缝最左侧点0, 5, 10, 15, 20, 25, 30, 35, 40 m共9个不同裂缝位置的上表面y方向位移大小, 由此得到数值模拟的结果, 并将其与已有文献结果进行对比, 如图4所示。

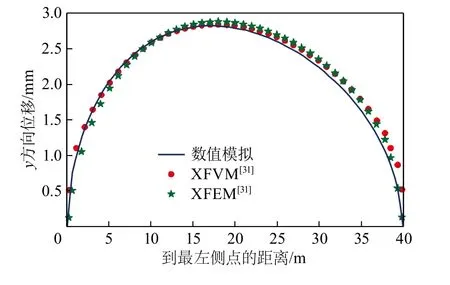
图4 模拟与已有文献结果对比Fig.4 Comparison of simulation and literature results

由图4可知, 数值模拟与文献[31]的结果吻合较好, 由此可以验证数学模型的正确性。

2.2 现场验证

为了进一步验证该数学模型的正确性, 以美国密西西比Barnett页岩气藏现场生产资料[6]进行验证, 此处的页岩气资源丰富, 如图5所示, 其开采经历了长达几年的时间并且有系统的监测数据, 便于开展模型验证。

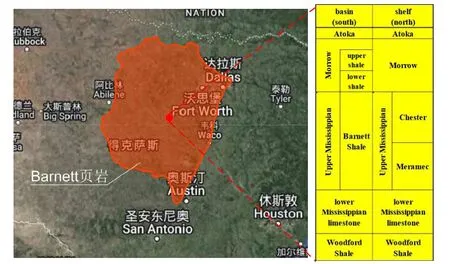
图5 Barnett页岩气藏研究区域与地质概况Fig.5 Study area of Barnett shale and the geological characteristics

该页岩气藏主要通过水力压裂、水平井开发的方式进行开采, 为便于计算, 笔者将整个Barnett页岩储层中的单个水力压裂区域建立模型进行数值仿真, 由此得到渗流量, 并与现场实际生产数据进行对比, 以验证模型的正确性。

所使用的数值模拟验证模型及边界条件如图6所示。Barnett页岩储层总尺寸为1 100 m×290 m,厚90 m, 笔者选择其中一条水力压裂裂缝及周边区域作为模拟模型, 区域总数量56个, 故模型尺寸选择为30.5 m×145 m的单个水力压裂区域, 厚90 m,采用自由三角形网格划分; 水力压裂裂缝长度为47.2 m, 压裂间距为30.5 m, 所使用的储层参数来源于美国New Mexico东南部的Barnett页岩[6,14], 见表2。

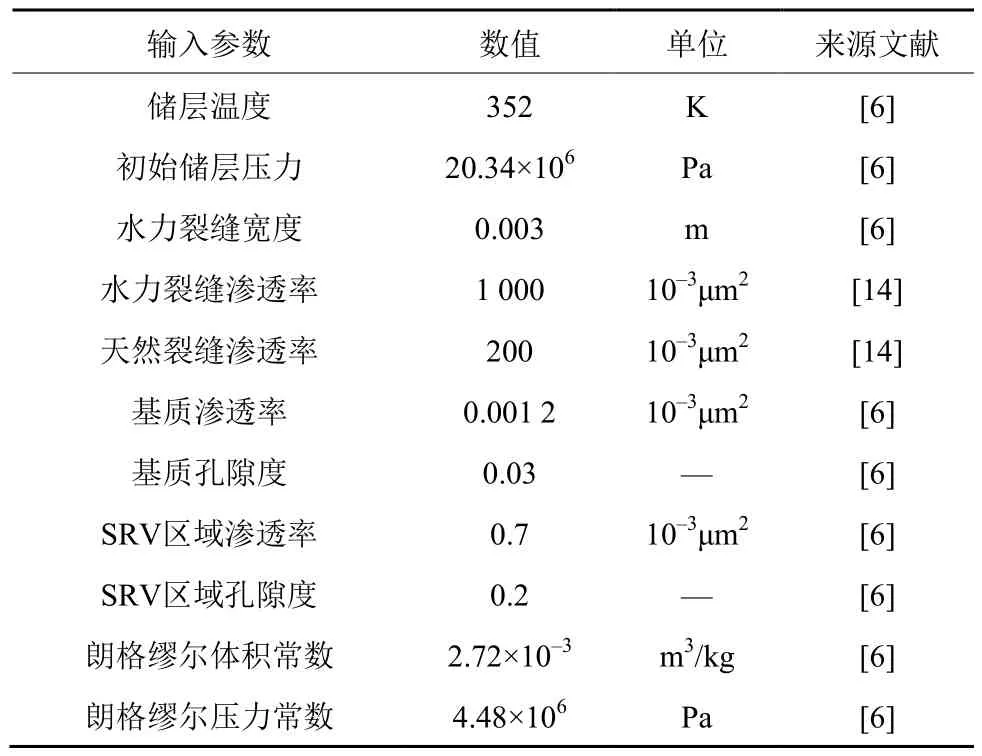
表2 数值模拟主要参数Table 2 Main parameters for numerical simulation of shale reservoirs

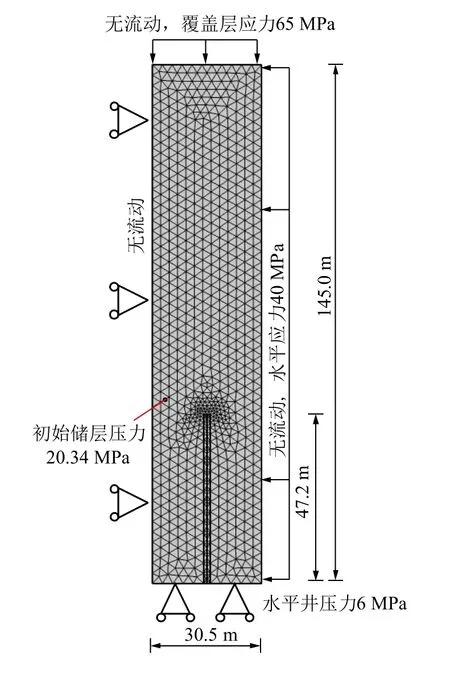
图6 数值模拟验证模型及边界条件Fig.6 Numerical simulation validation model and boundary condition diagram

基于COMSOL软件对页岩气储层模型进行数值模拟, 通过计算得到Barnett页岩储层内不同时间裂缝内的气体压力分布如图7所示。由图7可知, 由于水平井与页岩储层存在较大的压力差, 初始阶段气体会通过水力裂缝快速流向水平井(图7(a)), 待水力裂缝内的气压与水平井基本一致后, 水力压裂区内的气体将逐渐流入水力裂缝, 引起压裂区域气压下降, 随着时间的推移, 离压裂区较远处基质内的气体会逐渐流入水力压裂区, 进而流入水平井,这一过程逐渐由水平井朝远离水平井的区域发生扩散(图7(b)), 当基质内的气压接近开采压力时, 气体渗流过程会逐渐缓慢, 其气压分布如图7(c)所示。

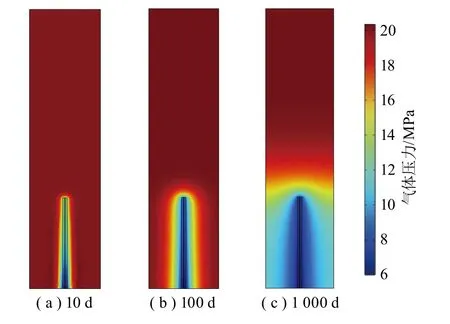
图7 裂缝内的气体压力分布Fig.7 Gas pressure distribution inside the crack

页岩气藏的数值模拟与实测结果对比验证如图8所示。由图8可知, 模拟结果峰值与现场生产数据峰值几乎一致。10~300 d内, 渗流量从2.18×105m3/d降低至5.39×104m3/d, 模拟结果与现场数据吻合较好; 300~1 600 d内, 渗流量从5.39×104m3/d降低至1.84×104m3/d, 模拟结果略高于现场数据,大致吻合, 推测可能是由于基质内水分的影响。模拟结果与现场实际生产数据整体吻合较好, 由此可验证模型的正确性。

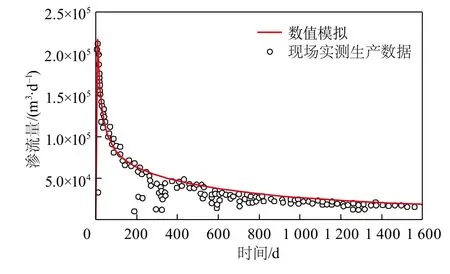
图8 模拟与实测结果对比Fig.8 Comparison of simulated and measured results

3 不同天然裂缝特征组合的影响

在页岩气实际生产过程中, 不同的储层条件相差各异, 其天然裂缝特征情况也各不相同[32], 不同的天然裂缝渗透率、密集度、倾斜角等条件都会对储层的渗流产生一定的影响。为研究不同天然裂缝特征变化对于储层渗流的影响, 使用COMSOL软件引入前文已经验证的数学模型, 通过生成随机裂缝, 有梯度地改变特征因素进行研究, 研究中将特征因素两两组合进行数值模拟, 以探究不同的天然裂缝特征组合对储层渗流产生的影响。模拟使用的储层模型尺寸为60 m×140 m的单个水力压裂区域, 厚20 m, 采用自由三角形网格划分; 水力压裂裂缝长度为80 m, 压裂间距为60 m, 所使用的其余基本储层参数与2.2节中参数相同, 见表2。

基本模型及边界条件如图9所示, 以长方形区域代表单个储层区域, 长直线段代表水力压裂裂缝, 其周围区域为裂缝区域, 随机的线段代表天然裂缝。

图9 天然随机裂缝模型及边界条件Fig.9 Natural random fracture model and boundary condition diagram

3.1 渗透率及密集度的影响

为了研究天然裂缝渗透率与密集度组合变化对页岩储层渗流的影响, 以50×10–3μm2为梯度设置了(50~500)×10–3μm2共10组不同的天然裂缝渗透率, 并用页岩储层区域单位面积内的天然裂缝总长度来表征密集度, 以0.08 m/m2为梯度设置了0~0.24 m/m2共4组不同的密集度, 通过数值模拟软件进行分别计算, 得到不同天然裂缝渗透率、密集度情况下的渗流量峰值, 并绘制3D曲面如图10所示。由图10可知, 该3D曲面沿着密集度的倾斜度较沿着渗透率的更大, 这说明天然裂缝密集度变化对页岩储层渗流的影响更为显著。此外, 由图10还可知, 渗流量峰值随着渗透率及密集度的增加, 始终保持着增加趋势, 但变化率却在不同的渗透率及密集度下有所不同, 这也说明在不同渗透率下, 密集度的增加对储层渗流的影响是不同的, 为了探究这种影响的大致规律, 选择渗透率为50×10–3μm2,500×10–3μm2的情况进行量化分析, 并且计算了比例, 结果见表3。由表3可知, 当密集度增加时, 渗流量明显提升, 渗透率为50×10–3μm2时的最大增加比例为3.5%, 500×10–3μm2时的最大增加比例为10.05%。由以上结果可知, 密集度的增加能够增加页岩储层渗透性, 且随着渗透率的增大, 密集度对页岩储层渗流的影响将会变得更大。

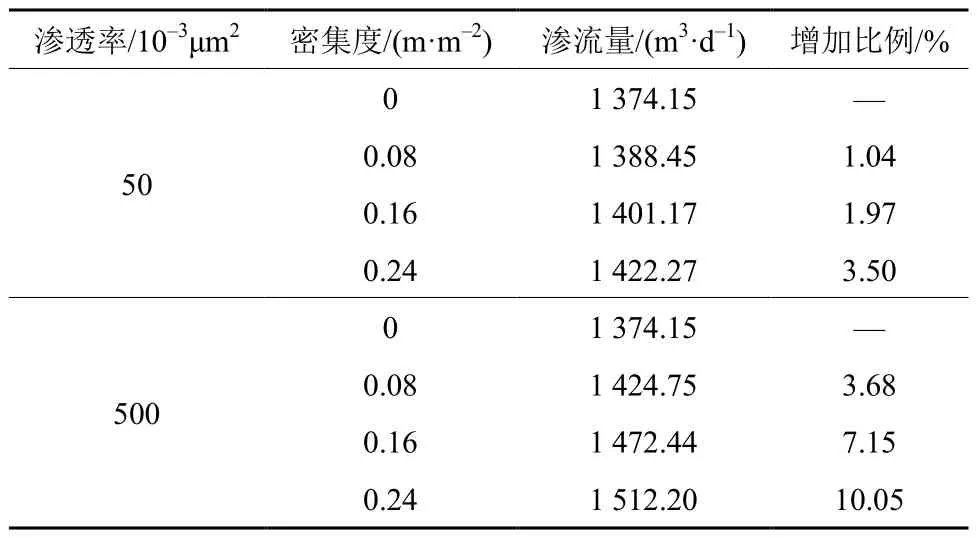
表3 渗透率及密集度组合时不同密集度的渗流量分析Table 3 Seepage volume analysis for different density with permeability and density combinations

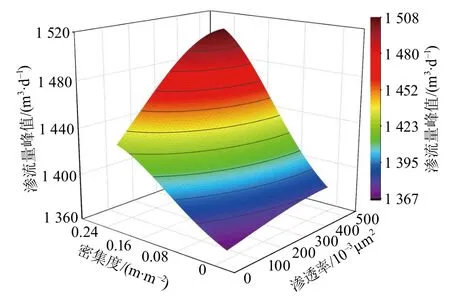
图10 不同裂缝密集度及渗透率情况下的渗流量峰值Fig.10 Surface plot of peak seepage volume for different fracture densities and permeabilities

同理, 在不同密集度情况下, 渗透率对储层渗流的影响也不相同, 选择裂缝密集度为0.08,0.24 m/m2时的情况进行对比, 结果见表4。由表4可知, 当渗透率提升时, 渗流量明显增加, 裂缝密集度为0.08 m/m2时的最大增加比例为2.61%, 0.24 m/m2时的最大增加比例为6.32%。由以上结果可知,渗透率的增加能够增加页岩储层渗透性, 且随着密集度的增大, 渗透率对页岩储层渗流的影响将会增加。

表4 渗透率及密集度组合时不同渗透率的渗流量分析Table 4 Seepage volume analysis for different permeability with permeability and density combinations

3.2 渗透率及倾斜角的影响

生成倾斜角度一致的天然裂缝模型如图11所示, 以30°为梯度设置了0°~90°共4组不同的天然裂缝倾斜角, 在不同的渗透率条件下, 通过数值模拟软件进行分别计算, 得到不同天然裂缝倾斜角、渗透率情况下的渗流量峰值, 并绘制3D曲面如图12所示, 由图12可知, 该3D曲面沿着倾斜角方向的变化率明显较沿着渗透率方向的更大, 这说明裂缝倾斜角对页岩储层渗流的影响更大。

图11 裂缝倾斜角模型Fig.11 Fracture tilt angle model

图12 不同裂缝渗透率及倾斜角情况下的渗流量峰值Fig.12 Surface plot of peak seepage volume for different fracture permeabilities and tilt angles

与3.1节类似, 选择对裂缝渗透率为50×10–3,500×10–3μm2的情况进行对比, 裂缝倾斜角为0°,90°的情况进行对比, 结果见表5, 6。由表5, 6数据可知, 渗透率为50×10–3μm2时的最小缩减比例为–3.99%, 500×10–3μm2时为–9.06%; 倾斜角为0°时的最大增加比例为5.92%, 90°时为0.33%。

表5 渗透率及倾斜角组合时不同倾斜角的渗流量分析Table 5 Seepage volume analysis for different tilt angle with permeability and tilt angle combinations

表6 渗透率及倾斜角组合时不同渗透率的渗流量分析Table 6 Seepage volume analysis for different permeability with permeability and tilt angle combinations

由以上结果可知, 倾斜角的增加会降低页岩储层渗透性, 并且随着渗透率的增大, 倾斜角对页岩储层渗流的影响将会变得更大; 而随着倾斜角的增大, 渗透率对页岩储层渗流的影响将会变得更小。

3.3 密集度及倾斜角的影响

在不同的密集度及倾斜角条件下, 通过数值模拟软件进行分别计算, 并绘制3D曲面如图13所示。由图13可知, 该3D曲面沿着密集度的变化率与沿着倾斜角的变化率大致近似, 需要通过具体计算进一步确定影响的相对大小。与3.1节类似, 选择密集度为0.08, 0.24 m/m2, 以及裂缝倾斜角为0°,90°的情况进行对比, 结果见表7, 8。

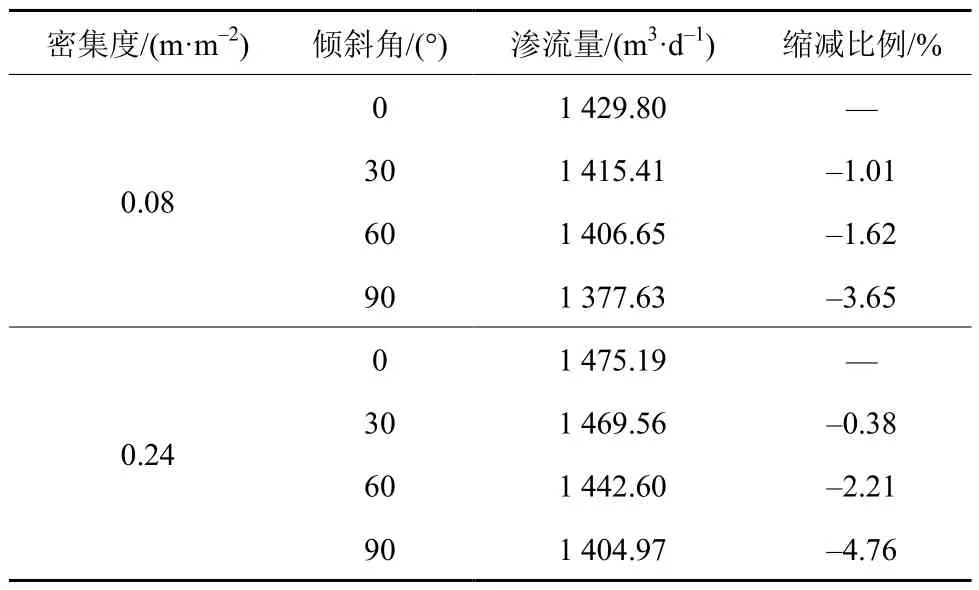
表7 密集度及倾斜角组合时不同倾斜角的渗流量分析Table 7 Seepage volume analysis for different tilt angle with densities and tilt angle combinations

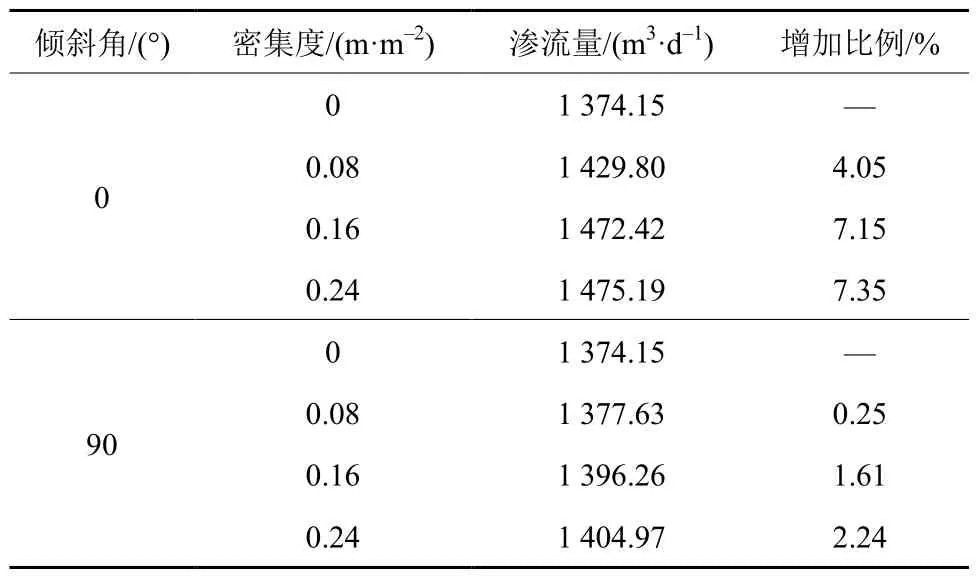
表8 密集度及倾斜角组合时不同密集度的渗流量分析Table 8 Seepage volume analysis for different densities with densities and tilt angle combinations

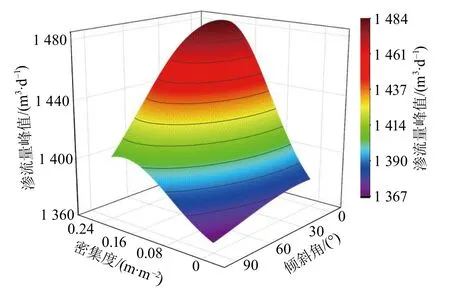
图13 不同裂缝密集度及倾斜角情况下的渗流量峰值Fig.13 Surface plot of peak seepage volume for different fracture densities and tilt angles

由表7, 8可知, 密集度为0.08 m/m2时的最小缩减比例为–3.65%, 0.24 m/m2时为–4.76%; 倾斜角为0°时的最大增加比例为7.35%, 90°时为2.24%。

对比以上数据可知, 随着密集度的增大, 倾斜角对页岩储层渗流的影响将会变得更大; 而随着倾斜角的增大, 密集度对页岩储层渗流的影响将会变得更小。倾斜角与密集度的变化对页岩储层渗流的影响大致近似, 密集度的影响略大一些。

4 结 论

(1)根据页岩储层水力压裂后的页岩气流动特征, 以质量平衡方程为基础, 推导了储层内的渗流场及应力场数学模型, 通过DFM模型模拟裂缝–基质内的流固耦合行为, 将数值模拟结果与已有文献结果进行对比, 验证了模型的正确性。

(2)天然裂缝渗透率、密集度、倾斜角均对储层渗透性有较明显的影响, 增加天然裂缝渗透率会加大倾斜角、密集度对储层渗流的影响, 对产气量的影响约10%; 增加密集度会加大渗透率对储层渗流的影响, 减弱倾斜角对储层渗流的影响, 对产气量的影响约6.3%; 增加倾斜角会同时减弱密集度、渗透率对储层渗流的影响, 对产气量的影响约7.4%。

(3)增加天然裂缝倾角导致的储层渗透性降低现象可能与天然裂缝、水力裂缝交叉数量降低相关, 所建立的数值模型能很好捕捉并说明这一宏观现象, 对现场水力压裂方案及参数的确定、提高页岩气的持续高产有重要指导意义。