永磁电磁混合悬浮系统垂向稳定性研究

侯晓杰 ，顾 蓉 ，杨炫淋 ，凌 浩 ，袁美全 ，肖子叶

（长安大学道路施工技术与装备教育部重点实验室，陕西 西安 710064）

0 引言

永磁悬浮系统的基本悬浮原理为Halbach 阵列间的永磁排斥力实现悬浮，这种悬浮方式结构简单，能实现静态稳定悬浮。但是永磁悬浮系统为非线性、难控性的系统，当有外力作用平衡位置发生变化时，系统的稳定性会降低，外力较大时甚至会引发安全事故[1]。因此，对永磁悬浮系统的稳定性进行研究具有重要意义。

文献[2]提出了一种永磁电磁间隔排列构成的混合磁阵列，其通过电磁铁可对空间磁场及电磁力进行主动控制，但其控制效果并不理想；文献[3]和文献[4]研究了一种电磁EMS 和永磁EDS 混合磁悬浮系统，其通过永磁EDS 提供悬浮力的同时利用电磁EMS 对悬浮力进行动态调节，达到主动控制的效果，但其存在磁场间的耦合问题；文献[5]和文献[6]研究了EDS 系统的六自由度动态稳定性，并采用线性二次型调节器较好地控制了系统的稳定性，但其结构较为复杂，且调节时间较长。

基于以上研究，本文提出了一种永磁电磁混合悬浮系统，推导出该系统的动力学模型，对该悬浮系统设计模糊PID 控制器，仿真出该控制器的控制效果，通过MATLAB/Simulink 建立了混合悬浮系统的仿真框图并仿真验证了该悬浮系统能够实现垂向稳定。

1 永磁电磁混合悬浮系统模型

1.1 永磁电磁混合悬浮系统建立

针对永磁悬浮结构的不可调控性，结合EMS 电磁悬浮技术的成熟性和可调控性，设计一种永磁电磁混合悬浮系统模型，如图1 所示。由上下Halbach 永磁阵列间的永磁力克服绝大部分负载力，电磁模块产生小部分电磁力克服负载力，当出现外界扰动力时，可由控制器控制电磁模块中电流的变化对悬浮系统进行可控调节。图1 中，x为混合悬浮系统悬浮间隙；m为混合悬浮系统的质量；f为外界扰动力；u和i分别为通入电磁模块的电压和电流；F1(x)为永磁阵列间的排斥力；F2(i,x)为电磁模块产生的电磁力。

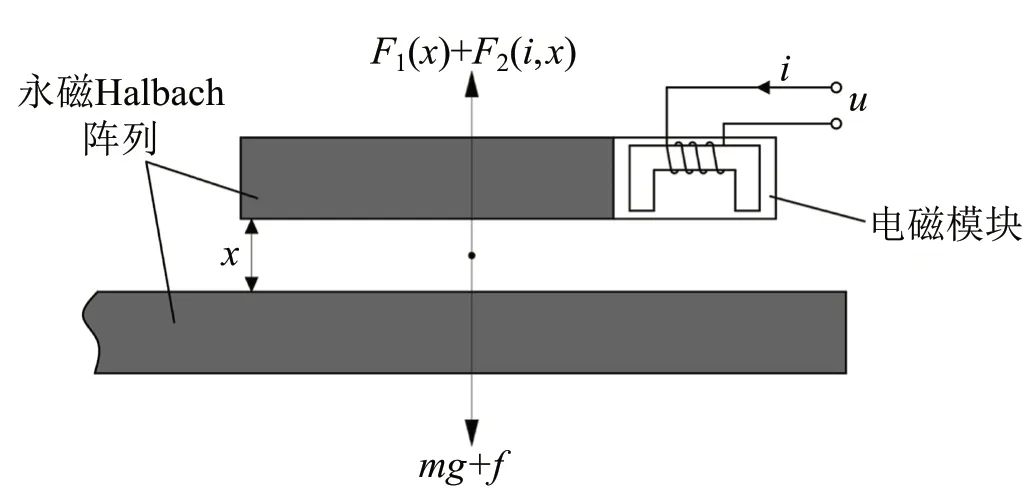
图1 永磁电磁混合悬浮结构

1.2 永磁电磁混合悬浮系统垂向动力学模型

假设永磁电磁混合悬浮系统仅有垂向位移，根据电磁学和动力学理论，以向下为正方向，可以得到该系统的垂向动力学方程[7]为：

式中，m为悬浮系统总质量；g为重力加速度；f为外界扰动力；μ0为真空磁导率；N为电磁模块线圈匝数；A为电磁模块铁心的有效截面积。

由式（1）可知，该悬浮系统为非线性系统，假定平衡点为（i0，x0），通过泰勒公式展开并忽略高阶小项得到系统的线性化形式：

式中，Δx为悬浮间隙变化量，Δx=x-x0；Δi为电流变化量，Δi=i-i0；kx和ki为混合悬浮系统悬浮力随x和i的变化率。

其中，系数矩阵：

即状态方程表示为：

由系统的能控矩阵Pc=[B AB]以及系统的能观矩阵Q=[C CA]T，可知Pc与Q的行列式均不为0，表明系统具备完全能控性与完全可观性[8]。

2 混合磁悬浮系统模糊PID控制器设计

2.1 模糊PID控制器设计

暂且忽略扰动力f，对式（2）进行拉普拉斯变换，可以得到悬浮间隙与电流之间的传递函数为：

通过PID 试凑法[9]，可取如下参数：KP=1.5×105，KI=6×106，KD=2 400。

模糊PID 控制器结构如图2 所示，模糊控制器包含偏差e和偏差变化率ec两个输入，经模糊推理输出三个参数的变化值ΔKp、ΔKi、ΔKd，PID 控制器通过三个变化值主动调节参数大小，从而能够实现PID 控制器的参数自行调节[10]。

图2 模糊PID 控制器结构

模糊PID 控制器的参数如表1 所示。选择输入变量和输出变量的隶属度函数为三角形函数，模糊控制器的三个输出变量ΔKp、ΔKi、ΔKd的模糊控制规则如表2、表3、表4所示。

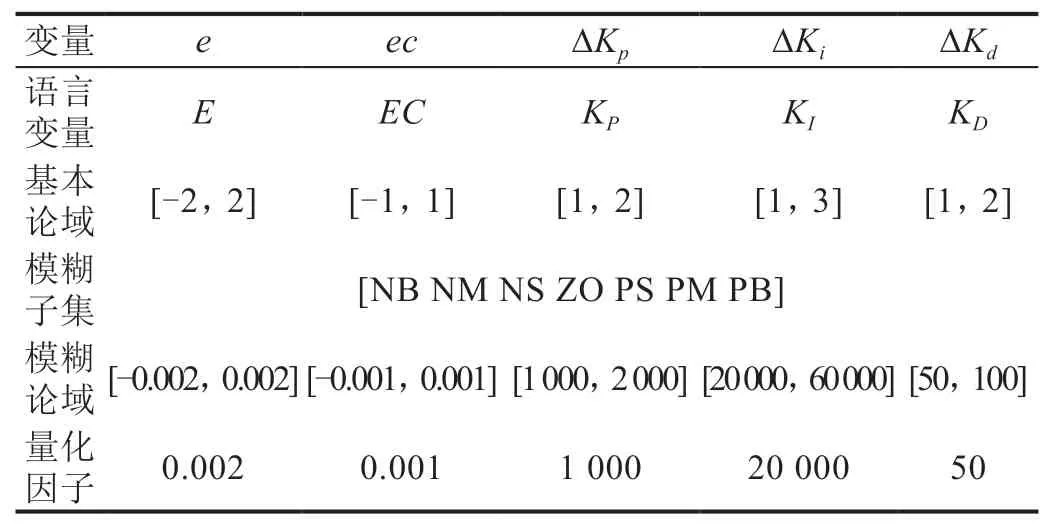
表1 模糊PID 控制器参数

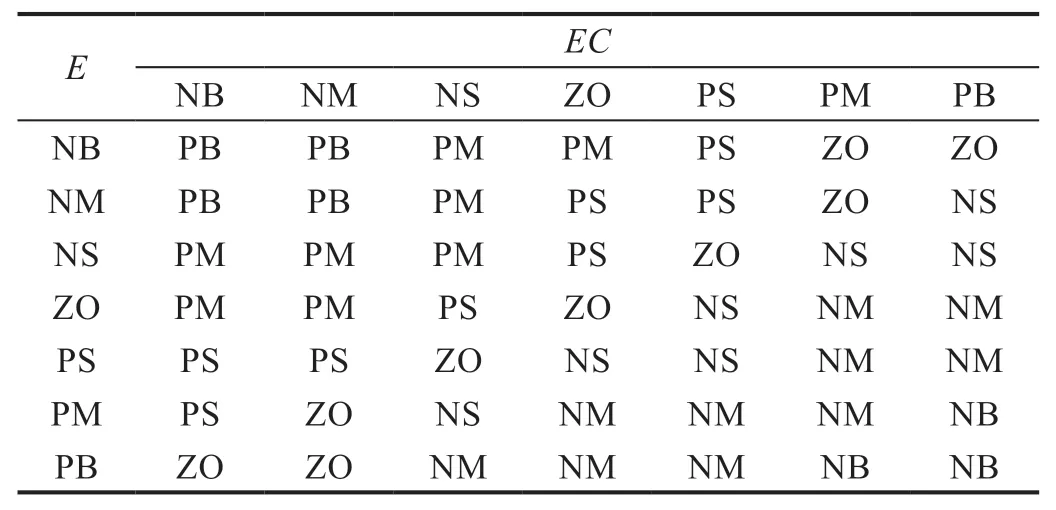
表2 ΔKp的模糊控制规则

表3 ΔKi的模糊控制规则

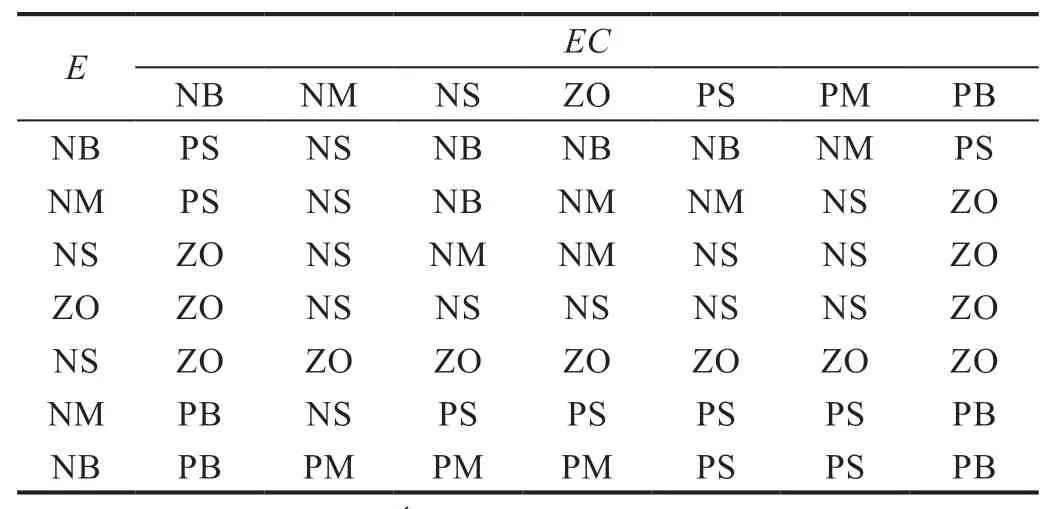
表4 ΔKd的模糊控制规则

通过解模糊可以得到PID 参数的修正量[11]，之后根据公式（8）得到控制参数。

其中：qp、qi、qd为比例、积分、微分的量化因子，Kp0、Ki0和Kd0为PID试凑得到的值。

2.2 模糊PID控制器仿真

首先在MATLAB 模糊控制工具箱中操作，将位移偏差E与偏差变化率EC两个输入变量与PID 参数的修正量ΔKp、ΔKi、ΔKd三个输出变量的论域范围、隶属度函数信息以及三个输出变量的模糊规则信息录入工具箱；其次利用Simulink 仿真工具将模糊控制器的输出信号与PID 的初始设定值相加输入到经典PID控制器，连接成模糊PID 控制器。建立的混合磁悬浮模糊PID控制系统仿真框图如图3所示。

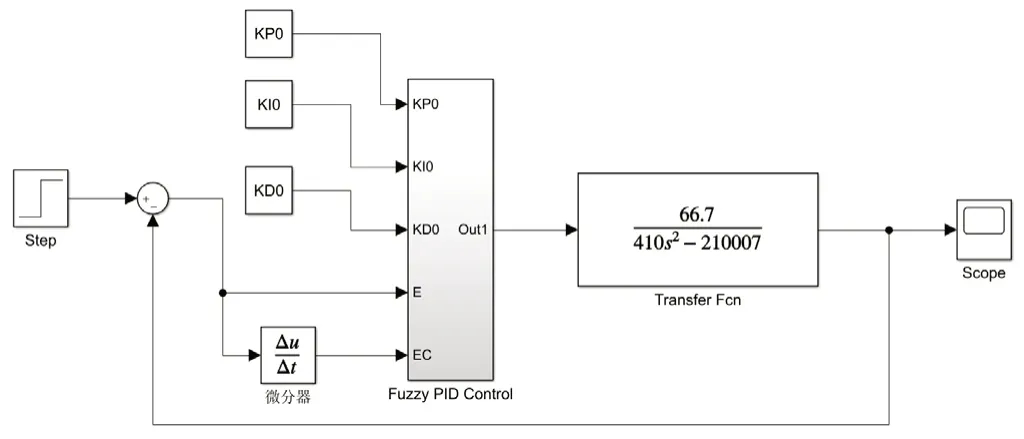
图3 混合磁悬浮模糊PID控制系统仿真框图

通过MATLAB 仿真得到单位阶跃下模糊PID 控制系统输出效果，如图4 所示。由图4 可知，模糊PID控制器的超调量小且调整时间不到0.2 s，说明模糊PID控制器动态特性优良，抗干扰能力强。

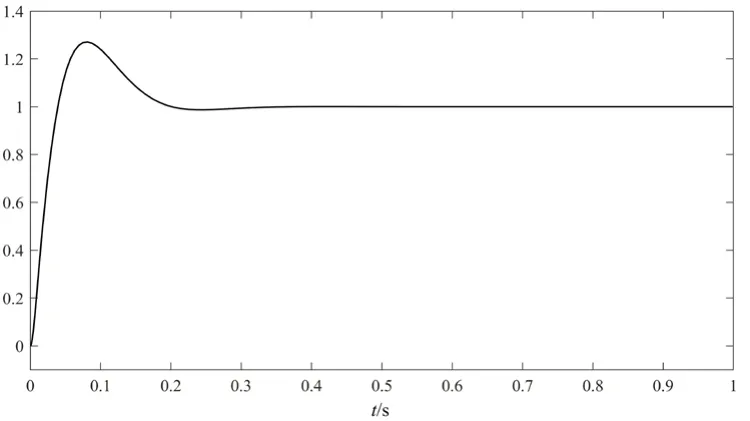
图4 模糊PID 控制器的输出效果

3 永磁电磁混合悬浮系统仿真分析

利用模糊PID 控制器在Simulink 中搭建永磁电磁混合悬浮系统仿真框图，如图5所示。

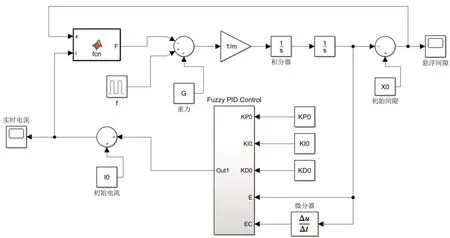
图5 永磁电磁混合悬浮系统仿真框图

为了验证永磁电磁混合悬浮系统的垂向抗扰动性能，现对以下3种情况进行仿真：1）无外界扰动力；2）外界扰动力为f=-50 N，加载时间分别为1 s和6 s，持续时间均为2 s；3）外界扰动力为f=150 N，加载时间分别为1 s 和6 s，持续时间均为2 s。

通过仿真得到悬浮间隙x与电磁模块通电电流i的波形，如图6、图7、图8 所示。无外界扰动力干扰时，系统在轻微震荡后稳定悬浮在0.02 m 的平衡位置，此时电磁悬浮模块的通电电流为2.994 A，与理论分析的平衡位置处电流3 A 存在微小偏差；当外界扰动力为f=-50 N 时，系统调整时间小于0.1 s，快速稳定后的电流约为2.1 A，与理论分析电流为下降趋势一致；当外界扰动力为f=150 N 时，快速稳定后的电流约为4.7 A，与理论分析电流为上升趋势一致，并且符合扰动力矢量增大、电流矢量增大的变化趋势。

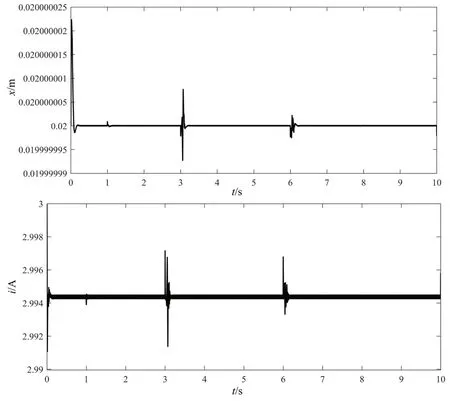
图6 无外界扰动力下悬浮间隙与电流的波形

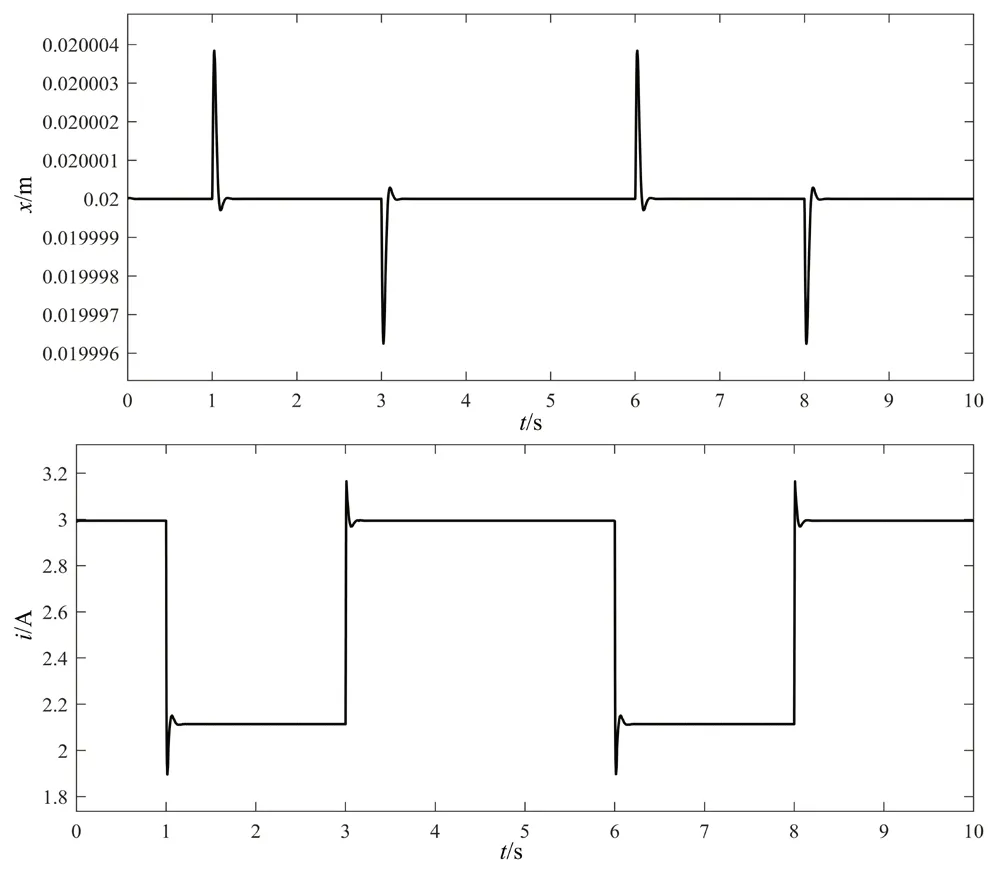
图7 外界扰动力f =-50 N 下悬浮间隙与电流的波形

图8 外界扰动力f =150 N 下悬浮间隙与电流的波形

由以上分析可知：永磁电磁混合悬浮系统的模糊PID控制器响应速度快、控制效果好、抗干扰能力强，能够使系统稳定悬浮于0.02 m的平衡位置。

4 结论

本文在永磁悬浮的基础上设计永磁电磁混合悬浮系统模型，基于永磁电磁混合悬浮动态特性分析，设计了模糊PID 控制器，并对其进行动态仿真，得到以下结论：

1）永磁悬浮结构能够产生强大的天然磁场，运用永磁悬浮能在很大程度上节约能源、降低能耗，但单一永磁悬浮结构不具备主动调控性，出现轻微扰动便会失去稳定悬浮状态。

2）通过仿真模糊PID 控制器的单位阶跃响应，发现模糊PID 控制器能实现超调量小、响应速度较快的性能要求，能够获得良好的动态和稳态性能。

3）通过分析不同外界干扰下悬浮系统的垂向稳定性，发现所设计的模糊PID 控制器能使系统稳定悬浮在0.02 m的平衡位置，并且在外界扰动力为-50 N、150 N时，系统均能快速响应后稳定悬浮在平衡位置。