便携式微波水分仪在仓储烟叶含水率检测中的应用

徐 俊，李 强，马盛力，黄 慧，陈 伟，詹 映

（1.上海烟草集团有限责任公司上海烟草储运公司，上海 200439；2.上海创和亿电子科技发展有限公司，上海 200092）

0 引言

原烟经过打叶复烤加工后，将200 kg 的成品片烟打包成箱，箱装片烟的水分应控制在11%～13%。为了在投料生产前让烟叶原料的外观质量、内在品质、感官品质等各方面得到显著改善，需要让烟叶在适宜的仓储养护环境下经过1～3 年的自然醇化[1-4]。但烟叶在库贮存的过程中伴随着客观贮存环境、贮存地区气候变化等因素，尤其是寒冷、高温、潮湿等易导致仓储环境的温湿度大幅变化，会导致烟叶含水率发生变化[5-9]。含水率变化不仅影响烟叶醇化过程中的品质变化，烟叶损耗更会造成经济损失，因此关注在库贮存的烟叶的水分变化就显得尤为重要[10-12]。

在烟叶醇化过程中，因受客观仓储条件限制，仓管人员的常规做法是根据作业标准和工作经验预防烟叶霉变[13-15]，尽管在库普查和日常检查时可以发现部分霉变情况，但是在不翻垛的情况下仅能检查顶层烟箱。而底楼仓间货垛的底层烟箱尤其容易产生湿底霉变等现象，但在不翻垛的前提下却难以对底层烟箱进行有效检查。因此，大部分发生霉变的烟叶是在出库检查环节，通过开箱查验来判定的，此时已经造成烟叶损耗不可逆转的结果，不仅导致了烟叶原料的浪费，更是干扰了卷烟配方生产的正常供应[16-19]。

因此，及时掌握烟叶原料水分变化情况，从而及时采取有针对性的养护措施，是烟叶原料防霉变的必然要求。目前，在烟叶原料仓储环节，水分检测主要是通过手感法和烘箱法进行。手感法个人主观性强，个体检测准确性差异较大，需要检测人员具备较高的技能和经验。烘箱法准确性高，但这是一种离线检测方法，环节多、耗时长，无法满足大面积检测库存烟叶水分的需要。此外，这两种方法都存在一个问题，当需要检查底层烟箱内烟叶的含水率时，需要搬运烟箱，这将耗费大量的人力、物力，因此需要一种不需要开箱即可准确探测烟箱内部烟叶含水率的技术[20-28]。

微波是一种电磁波，频谱范围为300 MHz～300 GHz，具有较强的穿透性，微波分析仪具有操作简单、检测速度快、样本制作简单、样本浪费少的特点。微波水分仪是利用微波穿透法实现水分检测的[29-36]，当微波通过含水物料和干燥物料时，微波在传播方向上的传播速度和强度会发生不同的变化，含水物料会使微波的传播速度变慢，强度减弱，通过检测穿过物料后微波的两种物理性质变化来计算物料中的水分含量。微波水分仪是基于ARM 平台的全自动在线检测系统，其能够实现实时精确监测水分，可以作为工业流程自动化控制中的纽带，持续提供可靠的水分数据。

1 材料与方法

1.1 材料和仪器

材料：试验选取2020 年贵州中部烟112 个样品，上部烟100 个样品，下部烟100 个样品；黑龙江中部烟100 个样品，总共412 个烟叶样品。

仪器：德国哈尔卡森公司的微波水分仪，德国MMM Venticell 111 烘箱，赛多利斯电子天平CPA324S（精度0.1 mg）。

1.2 测定方法

1.2.1 微波频谱的测定

采用德国哈尔卡森公司的微波水分仪测量烟箱的频谱，用微波水分仪分别测量烟箱其中一个角的上、中、下三点，得到三条频谱后求平均频谱，代表这个烟箱样品的微波水分仪频谱值。

1.2.2 含水率的测定

采用实验室烘箱测量样品标准数据，将测量完频谱三个点的样品各取一小把，大约20 g 左右，磨粉后，用天平称取10 g 左右，放入烘箱中，温度设置100 ℃，2 h 后取出样品，用天平称重后，进行含水率的换算，并将结果作为对应样品含水率的标准数据。含水率（%）=（样品称重前质量-样品称重后质量）/样品称重前质量*100%。

1.2.3 微波频谱预处理方法

在使用微波水分仪检测烟叶时，采集的信息中除含有样品的原始的化学信息外，还包含其他外在的干扰信息和噪声，二阶导数计算可以减少基线偏移、漂移和背景干扰造成的数据偏差。

二阶导数计算公式如下：

式中，g为导数窗口的宽度；i是某个样品数；x是导数前的频谱频率值；X是导数后的频谱频率值。

1.2.4 蒙特卡洛偏最小二乘交叉检验法

异常样本在微波水分仪整个模型的构建过程中会对模型存在很大的影响，这些奇异值会给模型的参数估计带来偏离，降低模型的精度与稳健性。蒙特卡洛偏最小二乘交叉检验法充分利用统计学的性质，能够检测频谱的奇异点。

算法具体步骤：1）用偏最小二乘法（PLS）确定最佳主成分数；2）用蒙特卡洛随机取样法取80%的样本作为校正集，建立PLS 回归模型，剩余部分作为预测集；3）循环2 000 次，得到各样本的一组预测残差；4）求各样本预测残差的均值与方差；5）若样本偏离主体，则从校正集中剔除。

1.2.5 偏最小二乘法（PLS）建模

1）设M为所有微波水分仪测得的频谱矩阵，S为对应的含水率。首先对M、S数据集进行标准化，记作V0、H0。

2）记t1是V0的第一个成分，t1=V0ω1，ω1是V0的第一个轴，为一个单位向量，即有||ω1||=1。

记u1是H0的第一个成分，u1=H0c1，c1是H0的第一个轴，为一个单位向量，即||c1||=1。

3）实施V0和H0在t1上的回归：

式（3）中，是V0在t1上的回归系数矩阵，V1是回归残差矩阵。式（4）中，是H0在t1上的回归系数矩阵，H1是回归残差矩阵。

然后，依据最小二乘回归求得：

同理可得r1：

4）回归残差矩阵分别记作V1和H1，提取含水率数据残差成分ω2：

然后，求第二个轴ω2和c2以及第二个成分t2和u2：

同理，实施V1和H1在t2上的回归：

5）求成分th=Vh-1ωh，ωh是矩阵最大特征值所对应的特征向量。如果根据交叉有效性，确定共抽取h个主成分t1,…,th可以得到一个满意的预测模型。则求H0在t1,…,th上的普通最小二乘回归方程为：

2 结果与分析

2.1 异常样本剔除

分别用马氏距离法、半数重采样法、蒙特卡洛偏最小二乘交叉检验法三种异常样本剔除方法对采集的频谱和含水率进行异常样本剔除对比分析，选择不同的异常样本剔除法建立偏最小二乘法（PLS）模型的结果，如表1 所示。结果表明，采用蒙特卡洛偏最小二乘交叉检验法剔除异常样本建立的偏最小二乘法（PLS）模型不仅校正标准偏差（RMSEP）最小，而且相关系数最大。因此，使用蒙特卡洛偏最小二乘交叉检验法不仅提高了模型的预测精度，而且还大大降低了异常样本带来的模型复杂性，使模型得到简化、稳定性好，能有效地反映烟叶水分信息。

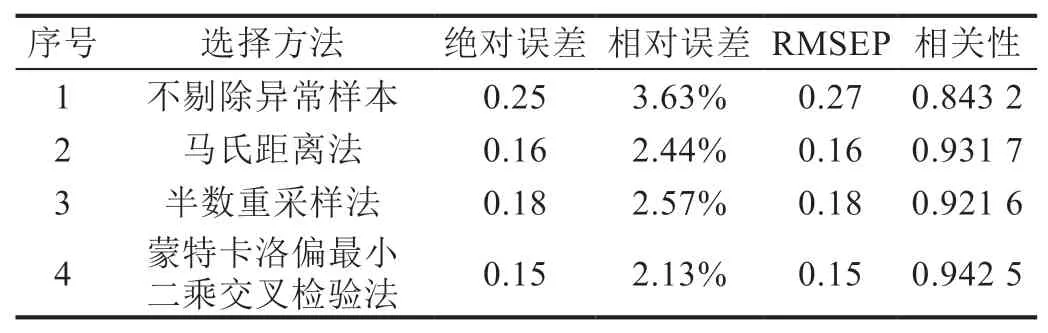
表1 不同异常样本剔除方法所建立的模型结果对比

2.2 贵州中部烟单部位模型的建立

取贵州中部烟112 个样品的频谱与对应的含水率，含水率分布如图1 所示。用二阶导数预处理方法剔除基线偏移、漂移和背景干扰，然后用蒙特卡洛偏最小二乘交叉检验法剔除异常样本，剔除6 个异常样本后，如图2 所示。剔除异常样本后总样品数量为106个。随机选取总样品的85%即90 个样品建模，总样品的15%即16 个样品进行验证，如图3 所示。然后用偏最小二乘法（PLS）建模，主成分选择5 个，建立的模型情况如图4 所示。

图1 贵州中部烟含水率分布

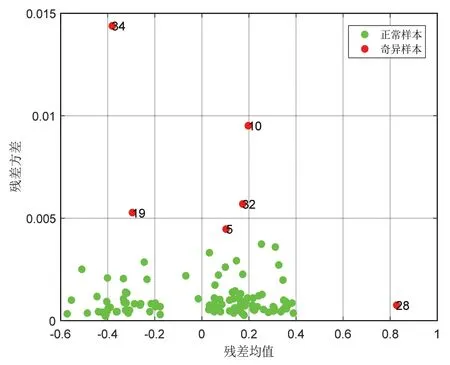
图2 贵州中部烟蒙特卡洛偏最小二乘交叉检验法剔除异常样本

图3 贵州中部烟校正和验证样本分布

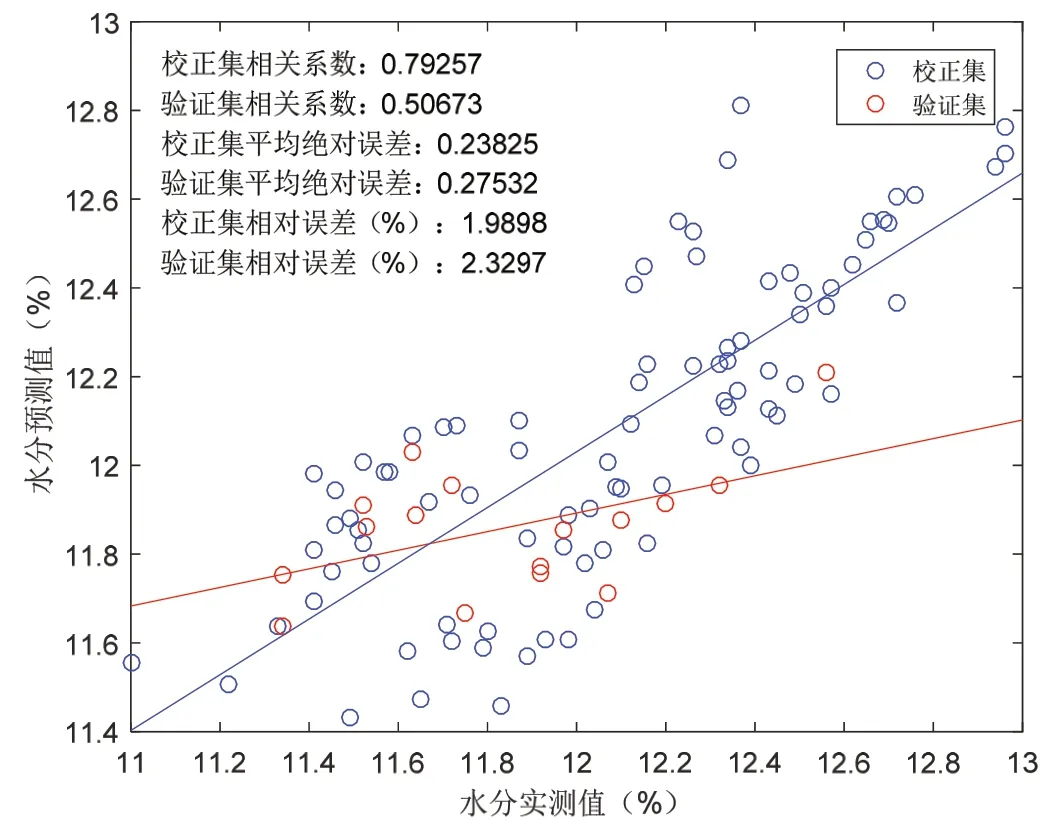
图4 贵州中部烟模型

从图2 中剔除大部分异常样本后，由图3 可以看出验证集样本分布在建模集之内，图4 显示建模后校正集平均绝对误差为0.24，校正集平均相对误差为1.99%；验证集平均绝对误差为0.28，验证集平均相对误差为2.33%。

2.3 贵州上中下部烟模型的建立

分别取贵州上、中、下部烟100、112、100 个样品的频谱与对应的含水率，含水率分布如图5 所示。用二阶导数预处理方法剔除基线偏移、漂移和背景干扰，然后用蒙特卡洛偏最小二乘交叉检验法剔除异常样本，剔除3 个异常样本，如图6 所示。剔除异常样本后总样品数量为309 个。随机选取总样品的85%即263 个样品建模，总样品的15%即46 个样品进行验证，如图7 所示。然后用偏最小二乘法（PLS）建模，主成分选择5个，建立的模型情况如图8所示。

图5 贵州上中下部烟含水率分布

图6 贵州上中下部烟蒙特卡洛偏最小二乘交叉检验法剔除异常样本

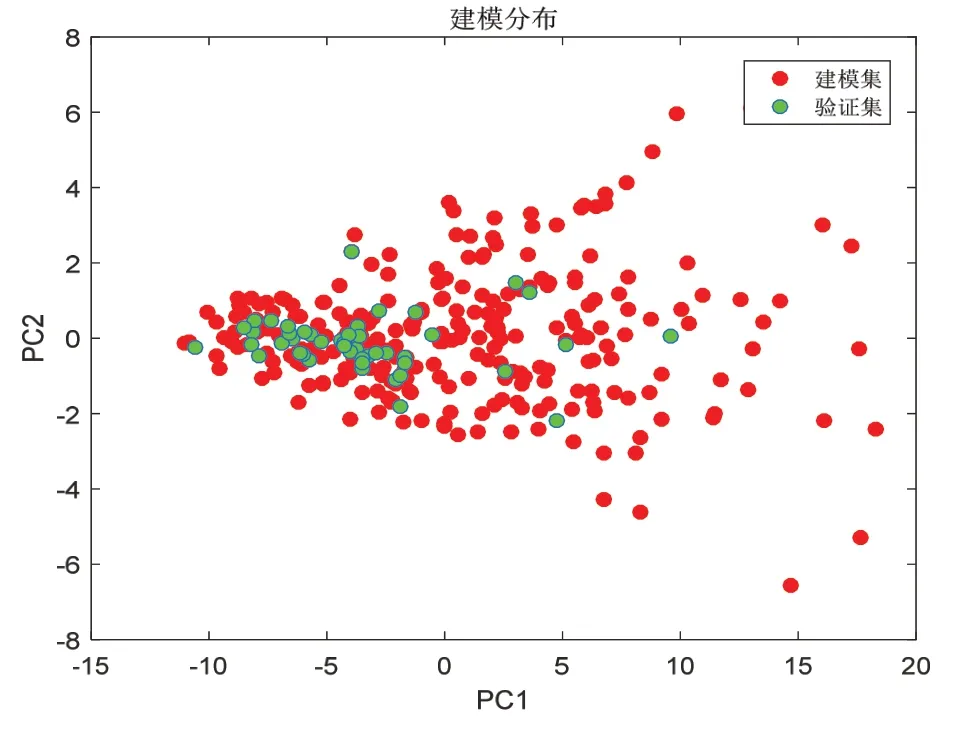
图7 贵州上中下部烟校正和验证样本分布

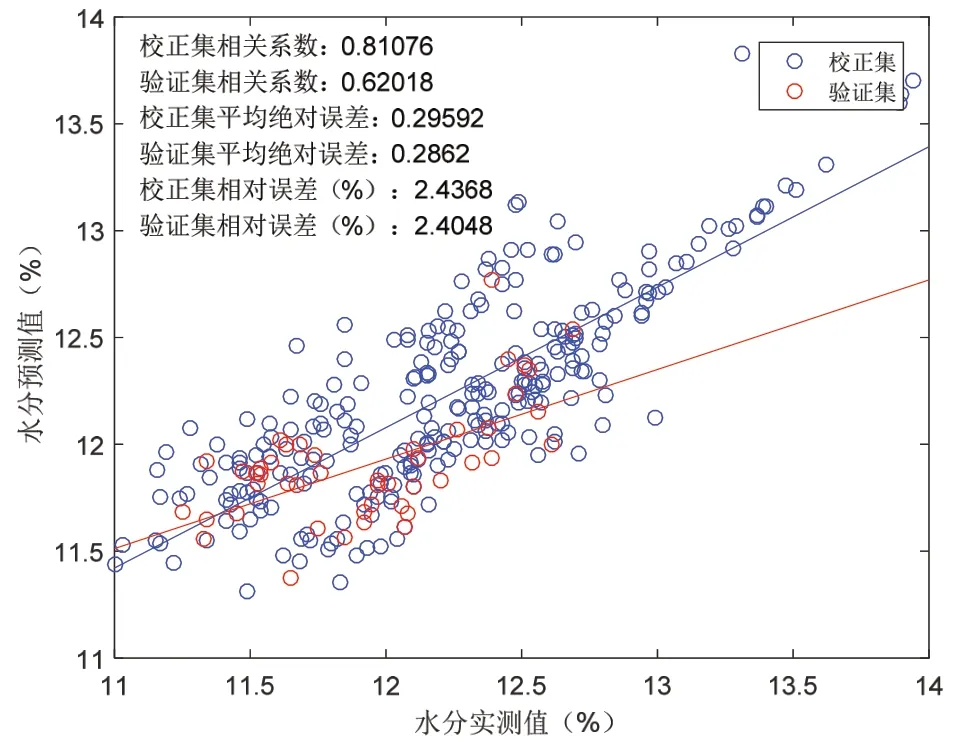
图8 贵州上中下部烟模型

从图6 中剔除大部分异常样本后，由图7 可以看出验证集样本分布在建模集之内，图8 显示建模后校正集平均绝对误差为0.30，校正集平均相对误差为2.44%，验证集平均绝对误差为0.29，验证集平均相对误差为2.40%。

2.4 贵州与黑龙江两个产地烟模型的建立

分别取贵州上、中、下部烟100、112、100 个样品以及黑龙江中部烟100 个样品的频谱与对应的含水率，含水率分布如图9 所示。用二阶导数预处理方法剔除基线偏移、漂移和背景干扰，然后用蒙特卡洛偏最小二乘交叉检验法剔除异常样本，剔除2 个异常样本，如图10 所示。剔除异常样本后总样品数量为410个。随机选取总样品的85%即349 个样品建模，总样品的15%即61 个样品进行验证，如图11 所示。然后用偏最小二乘法（PLS）建模，主成分选择5 个，建立的模型情况如图12所示。

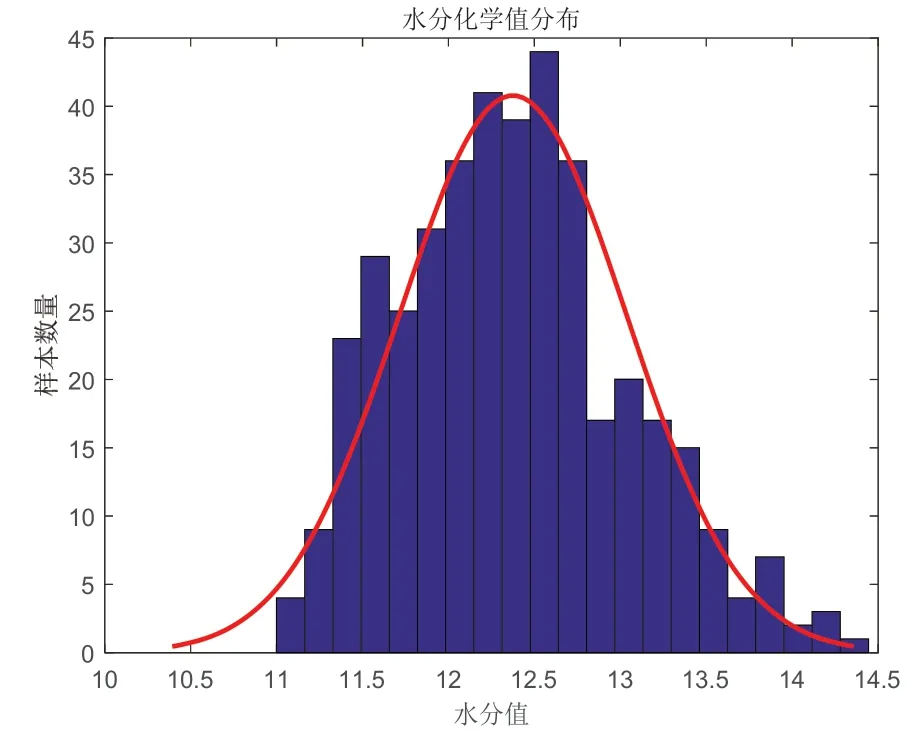
图9 贵州与黑龙江两个产地烟含水率分布

图10 贵州与黑龙江两个产地烟蒙特卡洛偏最小二乘交叉检验法剔除异常样本

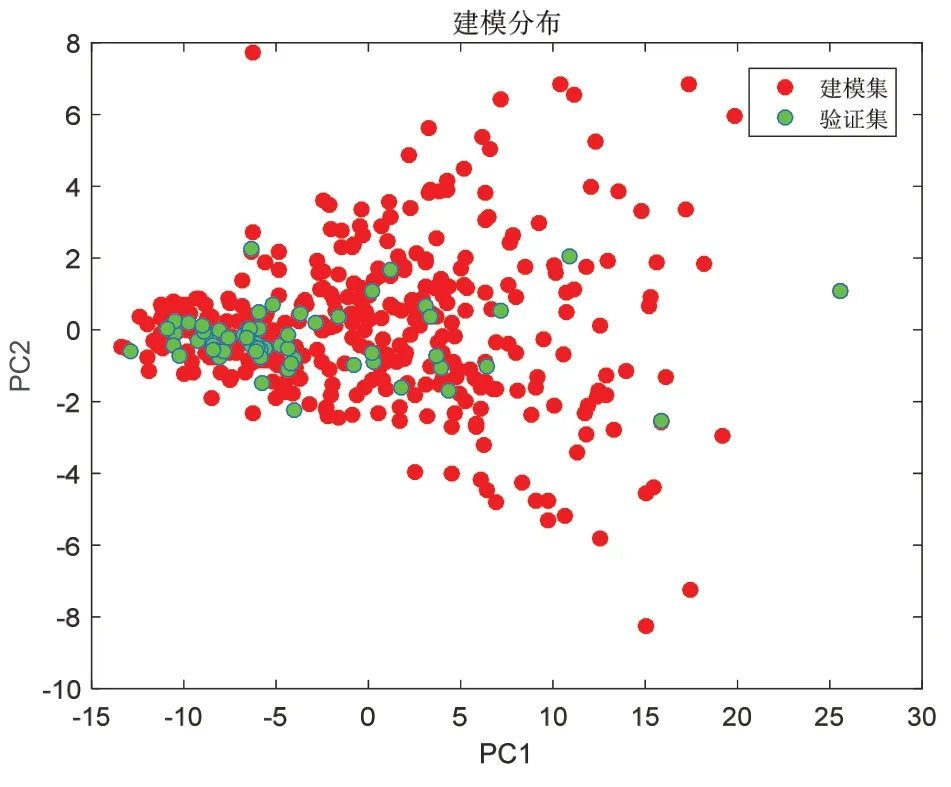
图11 贵州与黑龙江两个产地烟校正和验证样本分布

图12 贵州与黑龙江两个产地烟模型

从图10 剔除大部分异常样本后，由图11 可以看出验证集样本分布在建模集之内，图12 显示建模后校正集平均绝对误差为0.27，校正集平均相对误差为2.24%，验证集平均绝对误差为0.26，验证集平均相对误差为2.19%。

2.5 三个模型对比

三个模型的建模情况及验证情况如表2、表3所示。

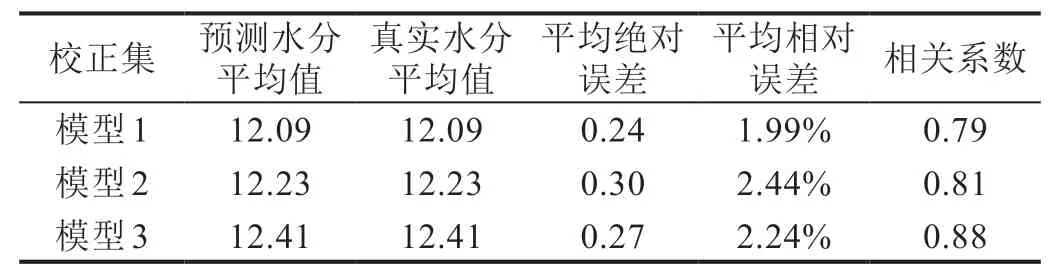
表2 三个模型的校正情况

表3 三个模型的验证情况

由表2、表3 可知，建立的三个模型相关性都在0.79 以上，相对误差都在3%以下，对所建立的模型进行验证，验证相对误差都在3%以下，而且数据量越多，验证的相关性越高。上述结果表明，无论是基于贵州单部位烟叶建立的水分预测模型，还是基于贵州多部位烟叶建立的水分预测模型，抑或是基于贵州和黑龙江两个产地烟叶建立的水分预测模型，模型的精度和稳定性都能满足实际应用的需求。

3 结论

1）在建立水分定量模型前，应首先剔除异常样本，这些异常样本可能含有信号值异常值或者异常水分组分，与其他样本存在显著差异。如果这些异常值参与建模，必然会降低含水率检测分析结果的准确性和可靠性，因此需要将这些异常样本剔除。采用蒙特卡洛偏最小二乘交叉检验法剔除异常样本较采用其他方法效果更佳。

2）该试验选择了偏最小二乘法来建立三个烟叶水分校正模型，并对模型进行了验证。结果表明，无论是用单产地单部位烟叶还是用单产地多个部位烟叶，或者是用多个产地的烟叶进行建模，所建立的模型的精度和稳定性都能够满足实际应用的需求。利用微波水分仪对储存中的烟叶水分进行无损检测分析，可减少人工测定所引起的误差，大大缩短检测时间，说明此方法可靠且准确，可有效地在不改变垛型、不移动烟箱、不破坏烟箱的情况下，实现烟垛棱边烟箱内烟叶含水率的快速在线检测，及时掌握烟叶水分变化情况，从而及时采取具有针对性的烟叶养护措施。