基于改进NSGA-II算法的RV减速器参数多目标优化研究*

杨昊霖,王茹芸,罗利敏,贡林欢,楼应侯

(1.宁波大学 机械工程与力学学院,浙江 宁波 315211;2.宁波中大力德智能传动有限公司,浙江 宁波 315211;3.宁波大学 科学技术学院,浙江 宁波 315211)

0 引 言

RV减速器是工业机器人、高端医疗器械等设备的核心部分。作为一种高精密减速器,传动压力角、传动效率等关键性能参数直接影响着设备的运行精度,从而严重影响RV减速器的使用寿命。

目前,国内外专家针对摆线轮压力角的设计提出了多种优化方案。徐宏海等人[1]采用了公式法,通过分析齿廓参数对压力角的影响,发现了平均压力角的变化规律;但其没有考虑因单目标优化而引起的减速器体积变大、传动效率变低等问题。纪姝婷等人[2]采用了公式法,基于摆线形成机理,推导了压力角的数学方程,发现了各机构设计参数对压力角的影响;但其没有考虑参数优化对传动效率的影响。王文涛[3]采用了将模数引入到摆线轮中的方法,发现了最小压力角随各种参数的变化规律;但是,其没有对多齿啮合的平均压力角进行研究。MOLODTSOV D[4]采用了遗传学算法优化参数,通过建立摆线轮齿廓方程和平均压力角方程,仿真分析了设计参数对压力角的影响规律;但是,其优化研究依旧停留在单目标优化阶段。

鉴于目前对压力角相关参数在多目标优化设计中的研究较少,笔者采用公式法推导出相互制约的一组优化目标(压力角、体积、传动效率),基于改进的NSGA-II算法进行多目标优化设计;最后,进行有限元分析和实验验证,以期为RV减速器的优化设计提供参考。

1 多目标优化问题概述

在旋转矢量(rotary vector,RV)减速器的多目标优化设计过程中,需先确立优化目标,建立目标函数,然后选择合适的设计变量,设置约束条件。优化目标之间必然会相互影响。

RV减速器由两级传动机构构成,低速级为摆线轮针齿传动机构,高速级为渐开线行星齿轮传动机构。其中:低速级部分是优化设计过程中的关键。

摆线轮的齿廓曲线如图1所示。

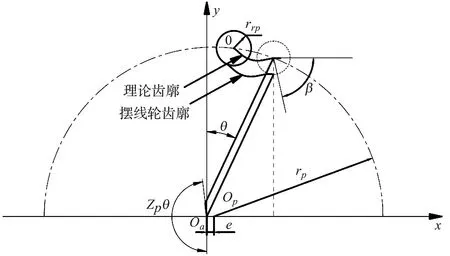
图1 摆线轮的齿廓曲线

摆线轮的标准齿廓方程表示如下:

x=rrpsinθ-esinzpθ+rpcosβy=rrpcosθ-ecoszpθ+rpsinβ

(1)

式中:rrp为针齿半径;e为偏心距;rp为针齿分布圆半径;zp为针齿齿数。

摆线轮与针齿压力角示意图如图2所示。

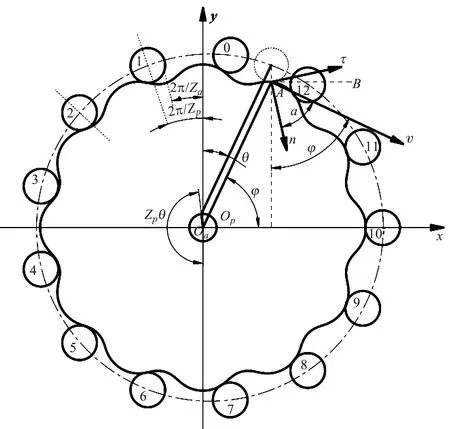
图2 摆线轮与针齿压力角示意图

依据摆线轮与针齿的压力角示意图受力分析,可求得0号针齿在啮合点A点处的压力角α0(θ),计算公式表示如下:

(2)

摆线轮上各啮合点的压力角的平均值表示如下:

(3)

式中:αi为第i个针齿与摆线轮啮合点的压力角,传动压力角为锐角,即αi≤90°[5]。

1.1 压力角与体积

最大接触力Fmax计算公式[6]表示如下:

(4)

为加快计算速度,笔者将两级减速传动部分的体积作为判断减速器体积的标准,所以目标函数中RV减速器的体积公式表示如下[8]：

(5)

式中:bj为渐开线齿轮的齿宽;bc为摆线轮的齿宽;m为渐开线齿轮模数;z1为输入齿轮的齿数;z2为行星轮的齿数。

针齿半径对体积及压力角的影响如图3所示。

图3 针齿半径对体积及压力角的影响

其他参数条件不变时,针齿半径与最大传动压力角成反比,最大传动压力角与体积成正比。

由最大传动压力角的加权变化规律,以及通过分析最大接触力计算公式(4)与RV减速器体积V的计算公式(5),可以推导出最大传动压力角与RV减速器的体积互相干涉。

因此,单独对压力角参数进行优化会导致减速器结构不够紧凑以及加工和安装困难,优化模型必须考虑减速器的体积。

1.2 体积与传动效率

RV减速器的传动效率会随扭矩的增加而提高,增加扭矩可以改善RV减速器内部的润滑系统[9],但减小减速器体积会限制扭矩和传动比大小,所以传动效率需纳入优化模型中。

由克莱依聂斯公式[10]推导出RV减速器的传动效率公式,表示如下:

(6)

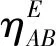
ηn与ηM的计算公式表示如下:

(7)

(8)

式中:P1为传递功率;v为齿轮节圆的圆周速度;b为齿轮宽度;ut为润滑油在工作温度下的运动黏度。

1.3 传动压力角与摆线轮修形

根据前人研究结果,即“正等距+负移距”的组合修形为最佳的修形方案[11],所以笔者所做研究均以该方式进行修形方案的设计。

正等距修形是指在加工摆线轮时,将刀具磨轮的半径增加一个距离Δrrp,即针齿半径由原来的尺寸rrp增加到rrp+Δrrp。

负移距修形则是固定摆线轮的位置,将刀具磨轮向摆线轮中心远离一个距离Δrp,即针齿的中心圆半径由rp变为rp-Δrp。

将修形参数代入式(1)中,即可得到摆线轮经过正等距与负移距修形后的齿廓方程[12],表示如下:

(e-k1(rrp+Δrrp)S)cosiHθ

(9)

式中:iH为摆线轮和针齿的传动比;S为摆线轮和针齿的综合系数。

其中:S=(1+k12-2k1cosφ)1/2。

笔者利用MATLAB编程,得出不同修形量对于摆线轮传动压力角的影响规律。

等距修形量对传动压力角的影响规律如图4所示。

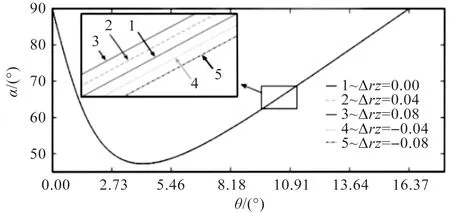
图4 等距修形量对传动压力角的影响规律

移距修形量对传动压力角的影响规律如图5所示。

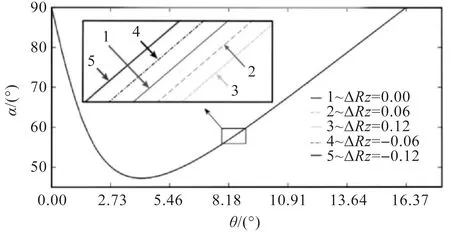
图5 移距修形量对传动压力角的影响规律

根据优化后的平均压力角值可反选出更合适的等距修形量与移距修形量,以此优化修形方案。

2 数学模型建立

2.1 改进的NSGA-II算法程序

笔者采用的改进NSGA-II算法基于非支配占优排序遗传学算法(non-dominated sorting genetic algorithm-Ⅱ,NSGA-II)改进了交叉算子系数生成,且拥有更为合理的排挤机制,可根据自变量范围矩阵随机编码生成种群,具有解集分布性好、时间复杂度低、收敛速度快等优点[13]。

该算法改进之处在于:NSGA-II算法选择用于计算个体拥挤度的参考点,是按各个目标分别进行选择。笔者采用多个目标综合选择法,这样使得拥挤度的计算与筛选更为准确。

改进的NSGA-II流程图如图6所示。

图6 改进的NSGA-II流程图

2.2 约束与变量设置

对于约束的处理,笔者采用基于拥挤距离的非占优排序法[14]。

先定义解的反约束量bi(x)表示如下:

(10)

然后,定义总约束量φ(x)表示如下:

(11)

式中:ci(x)为目标函数。

模型中存在如齿轮模数、齿数等离散变量。计算过程中产生的子代会出现无定义的值,需要进行后处理。笔者对变量进行上下随机取整后得到优化圆整值。

整数处理方法表示如下:

(12)

对于非整数,需要将所有可取值共同排序。例如模数值mi在2～2.5之间,则使结果在2、2.5这两个处理结果取相同的概率。

处理方法表示如下:

(13)

2.3 设计变量

如前所述,笔者将整体优化目标相关的设计参数(变量)确定为针齿分布圆半径rp、渐开线齿轮模数m、短幅系数k1、针齿半径rrp、针径系数k2、针齿齿数zp、输入齿轮齿数z1、行星轮宽度bp、摆线轮宽度bc、偏心距e等。

设计变量矩阵表示如下:

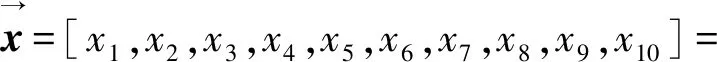
(14)

式中:m为离散变量;zp,z1为整数变量;其余为连续变量。

2.4 多目标函数建立

笔者根据式(1)～式(9)建立以RV减速器整机综合性能为优化目标的目标函数。

2.4.1 减速器的体积

减速器体积的目标函数表示如下:

(15)

2.4.2 摆线轮平均传动压力角

摆线轮平均传动压力角的目标函数表示如下:

(16)

2.4.3 减速器的传动效率

笔者针对取输出转速为15 r/min条件下的最高传动效率进行研究。

传动效率的目标函数表示如下:

(17)

2.5 约束条件设置

根据机械设计手册,确定各约束条件的取值范围[15]。约束条件主要为8个。

1)输入齿轮的齿数

已知在标准齿轮的设计中,为避免根切现象而限制最低齿数为17,但若是齿轮材料满足齿轮弯曲强度,即使齿数低于17也只会出现轻微的跟切现象;而且若使用成型法或变位加工法加工齿轮,根切现象也不会出现。所以为了获得更紧凑的结构,优化程序无需对输入齿轮的齿数进行约束[16]。

2)短幅系数

短幅系数k1,取值范围0.75～0.9,计算公式表示如下:

(18)

3)针齿系数

针齿系数k2,取值范围1.0～1.6,计算公式表示如下:

(19)

4)针齿半径

针齿半径rrp必须小于最大曲率半径ρ0,ρ0计算公式表示如下:

(20)

5)针齿中心圆直径

针齿中心圆直径dp的取值范围为[144,164]mm。

6)摆线轮宽度

摆线轮宽度bc取值范围为[0.1dp,0.2dp]mm。

7)摆线轮接触强度

按摆线轮所用材料(GCr15),许用接触强度σHP选1 300 MPa～1 500 MPa,摆线轮接触强度σHt满足条件如下:

(21)

8)径向间隙

摆线轮修形产生的径向间隙Δr,取值范围为[0.01,0.1]mm。其计算方法表示如下:

Δr=Δrrp-Δrp

(22)

2.6 计算实例

2.6.1 多目标优化求解

此处以某公司220BX型RV减速器为例,笔者将该型号减速器参数初始数据输入进行优化[17-18]。

改进NSGA-II优化迭代图如图7所示。

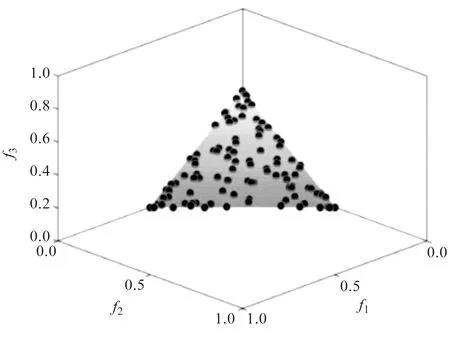
图7 改进NSGA-II优化迭代图

图7中:圆点表示迭代700次后的帕雷托最优解集。可以看出,解集在整个搜索域范围分布均匀,即各优化目标之间相互平衡制约,使结果不会偏向某一目标。笔者在最优解集中采用模糊集合理论[19]选出一组最优解。

某公司220BX型RV减速器优化结果如表1所示。

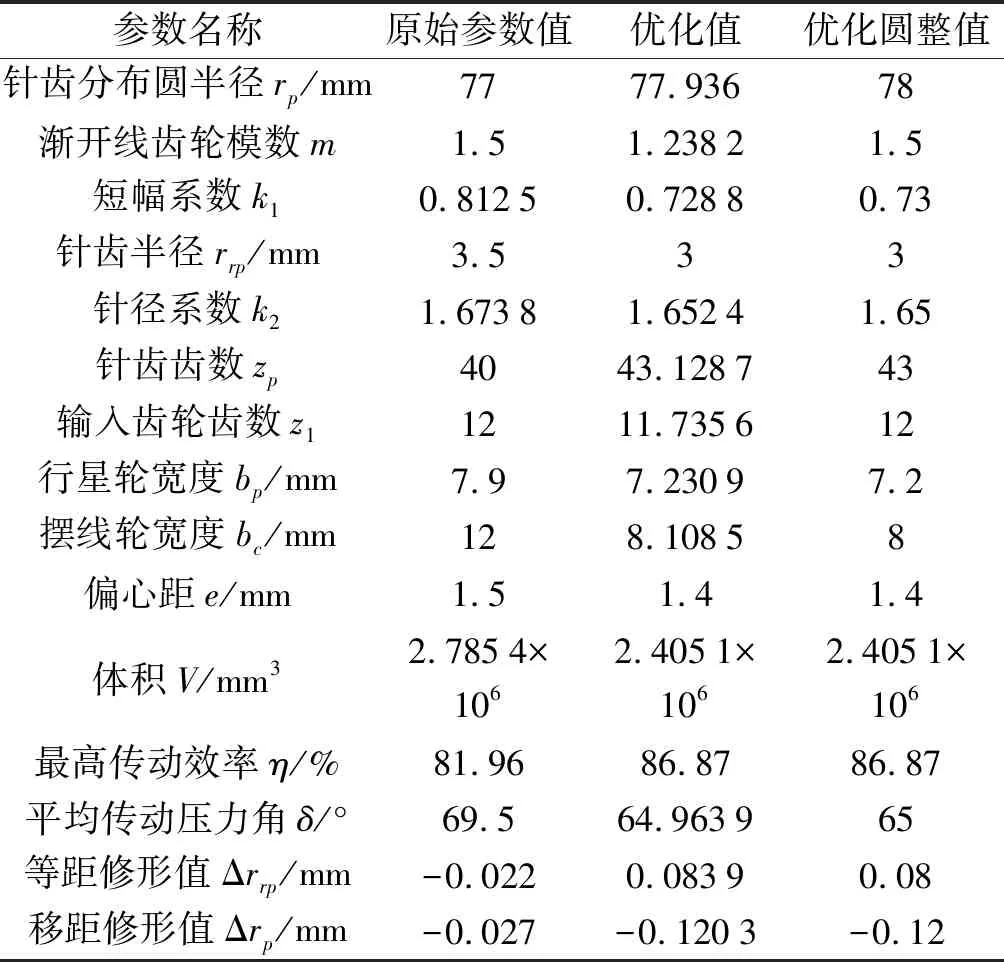
表1 某公司220BX型RV减速器优化结果

由表1可知:与原始参数值相比,多目标优化后的减速器在其平均传动压力角、体积、传动效率各参数上均有了一定程度的优化,其中,平均压力角减小了10.94%,体积减小了11.47%,传动效率提高了4.9%。

以上结果表明,多目标优化模型具有可靠性,能够综合提升RV减速器的性能。

2.6.2 优化模型的静强度应力分析

笔者利用SolidWorks建立RV减速器的3D模型,对模型进行简化,再对简化模型进行有限元分析,通过仿真计算校核模型的合理性[20]。

各零件材料参数如表2所示。

表2 各零件材料参数

整机模型如图8所示。

图8 整机模型

笔者对模型进行简化,去除如倒角、输出行星架等不影响计算结果的局部细节结构,然后进行网格划分。

网格划分如图9所示。

图9 网格划分

网格类型为C3D8R,数量共计96 989个。笔者设置边界条件为太阳轮与参考坐标原点刚性耦合,针齿壳、行星架固定,施加784 N·m的转矩,并约束渐开线行星轮和摆线轮的轴向位移;最后,对模型进行求解。

高速级传动应力分布如图10所示。

图10 高速级传动应力分布

由图10可知,高速级传动系统的最大应力位于太阳轮与行星轮接触处,最大应力为182.5 MPa,未达到材料的屈服强度。

低速级传动应力分布如图11所示。

图11 低速级传动应力分布

由图11可知,低速级传动系统中应力最大值在曲柄轴与摆线轮接触处,其最大值为208 MPa。

以上特征均符合RV减速器的设计原理[21],说明上述优化设计是合理的。

3 传动效率对比实验

为了验证优化设计的可行性,笔者针对实验样机进行传动效率的对比实验。

RV减速器的专用实验平台如图12所示。

图12 RV减速器传动效率试验台

该实验设备由驱动电机部分、2个扭矩转速传感器、温度传感器、实验用RV减速器、磁力制动器和手动控制器6个部分组成。

实验仪器主要参数如表3所示。

表3 实验仪器主要参数

针对优化后的摆线轮、针齿、输入齿轮,笔者采用齿轮加工平台以及其他设备进行加工。

齿轮加工平台如图13所示。

图13 齿轮加工平台

齿轮加工平台工作温度设置为25 ℃,输入速度设置为5 r/min～15 r/min,扭矩设置为0 N·m～1 500 N·m,时长设为60 s,采集频率为5 Hz。

传动效率实验数据如表4所示。

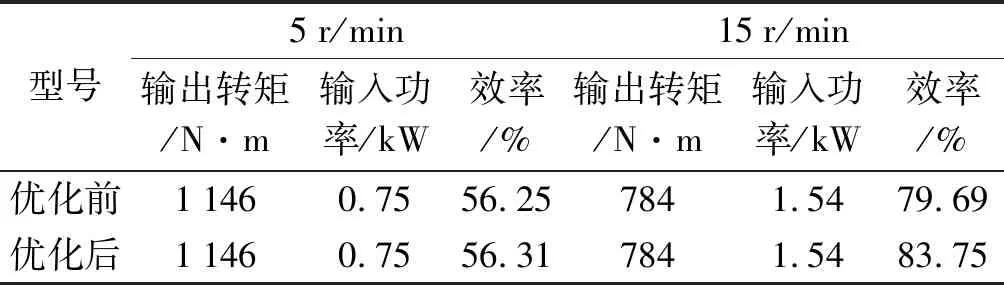
表4 传动效率实验数据

从表4的数据中可以看出:通过样机对比实验测试得到的输出转矩为784 N·m时,220BX型RV减速器在优化前的传动效率均值为79.69%,优化后的传动效率均值为83.75%,基本符合预期结果。

由此可见,采用RV减速器参数多目标优化模型不仅可以优化传动压力角,同时可以减小RV减速器体积,还可以有效提高减速器的传动效率。

4 结束语

笔者采用改进的NSGA-II算法,运用公式法推导出了摆线轮平均传动压力角、体积及传动效率之间的制约关系,并以此为目标函数,完成了RV减速器建模和优化方案的设计任务(该优化结果能够在保证摆线轮平均传动压力角减小的同时,减小RV减速器的体积,并提高传动效率,优化修形方案);最后,进行了有限元分析和传动效率对比实验,验证了多目标优化的有效性。

研究结果表明:

1)采用数学公式分析了RV减速器结构参数的影响因素,推导出了平均传动压力角、体积及传动效率为一组优化目标;以10个变量、3个目标函数、8个约束条件建立了多目标优化数学模型;

2)采用改进的NSGA-II算法对目标函数进行优化,通过ABAQUS有限元分析与传动效率对比实验,验证了该模型可以用于有效优化目标函数。

在后续研究中,笔者将以上述研究成果为参考,通过在优化目标中加入传动误差、啮合回差等目标函数,以此来优化设计参数,并在多目标优化程序中加入相关的约束条件和变量以进行建模,从而进一步提升RV减速器的综合性能。