基于最小势能原理的双渐开线齿轮载荷分布研究*

姜 宇,樊智敏,姜春雷,孙旭睿,闵令竹

(青岛科技大学 机电工程学院,山东 青岛 266061)

0 引 言

传统齿轮轮齿接触线载荷分布通常采用数值求解方法,通过求解齿面的三维弹性变形来确定;而双渐开线齿轮在齿腰分阶,齿面接触情况较为复杂,最大接触应力值通常出现在下齿面靠近齿腰位置,会产生载荷沿接触线分布不均的现象,导致齿面的润滑状态、齿侧间隙等发生变化;严重时会使油膜破裂,出现润滑失效,导致齿轮传动系统发生胶合破坏、齿面疲劳点蚀与齿面磨损等损伤。

因此,对双渐开线齿轮进行载荷分布的研究,对齿轮传动系统中的应力分析、润滑分析和动力学分析等具有重要意义。

齿轮传动时,共轭齿廓位置和啮合的轮齿数目不断发生变化。ISO[1]和AGMA[2]标准基于线弹性理论,根据实际经验和试验结果,提出了载荷分布系数方法,该方法仅适用于齿轮初步设计阶段中的强度校核,计算结果并不精确。WANG Jian-hong和CHANG Le-hao等人[3-4]提出了直齿轮的承载接触分析方法,将齿轮变形分为线性全局和非线性局部两部分,并利用有限元法计算线性全局,利用接触力学理论计算非线性局部;但该方法的齿轮变形划分较为复杂。JABBOUR T等人[5]将斜齿轮沿齿宽方向等分为若干片,每一片等效为直齿轮,通过计算直齿轮的啮合刚度获得斜齿轮的载荷分布;但直齿轮片的啮合齿廓必须是连续的。ZHANG Yi等人[6]结合齿轮接触分析技术、有限元法和线性规划法,提出了斜齿轮的承载接触分析方法,借此方法获得了齿轮副的载荷分布规律。PEDRERO J T等人[7-9]应用最小弹性势能原理,提出了直、斜齿轮的载荷分布模型,近年来该模型得到了广泛应用。PENG Yan-jun等人[10]在PEDRERO模型的基础上,建立了考虑轮齿修形和安装误差的斜齿轮载荷分布模型,采用基于固定点迭代方法的数值计算策略求解了模型;但该模型计算势能时未考虑基体势能。MARQUES P M T等人[11-13]采用有限元法计算了柔度矩阵,在获得齿面弹性变形的基础上计算了弹性势能,使计算较为准确;但齿面变形使计算过程相较于PEDRERO模型更复杂。LI Shan-ran等人[14]在考虑了轮齿根部势能的基础上,采用实际重合度代替理论重合度,计算了斜齿轮载荷分布;但该模型仅适用于齿轮特殊工作状态。

分阶式双渐开线齿轮是综合渐开线齿轮与双圆弧齿轮的一种新型齿轮[15],其在齿腰附近分阶,齿廓由齿根渐开线、齿顶渐开线和齿腰过渡圆弧曲线组成,且两端渐开线成阶梯式分布。分阶式双渐开线齿轮简称为双渐开线齿轮(下同)。

YIN Zhao-ming等人[16-18]根据“分段法[16]”思想,建立了双渐开线齿轮的热弹流润滑模型,研究了双渐开线齿轮的温度分布规律。陈亮等人[19]考虑了分形齿面粗糙度,求解了双渐开线齿轮时变啮合刚度,分析了齿面形貌与摩擦等对啮合刚度的影响。潘毅等人[20]利用ADAMS建立了柔性体双渐开线齿轮模型,降低了齿轮仿真过程中的震动波动,保证了齿轮运动的平稳性。

但上述研究过程中所涉及的载荷分布均考虑为沿接触线方向均匀分布,与其实际工作状态差别较大,接触线上的载荷非均匀分布,使得载荷计算困难。现有的方法或过于简化导致精度不足,或过于复杂使得计算量大、耗时长,并不适用于双渐开线齿轮载荷分布研究。

因此,笔者采用“分段法”将双渐开线齿轮接触线等分为若干段,基于最小弹性势能原理,建立双渐开线齿轮载荷分布模型,综合有限元法对轮齿载荷分布进行研究;最后将双渐开线齿轮的载荷分布与普通渐开线齿轮的载荷分布进行对比分析,并研究输入扭矩、齿宽对双渐开线齿轮载荷分布的影响。

1 双渐开线齿轮时变接触线长度分析

在某一瞬时啮合时刻,主动轮啮合平面上各位置的接触线L1、L2和L3,如图1所示。

图1 啮合平面t时刻接触线位置

即将完全啮出时,H与N1的距离N1H为:

N1H=N1B1+B·tanβb

(1)

式中:B为齿宽。

笔者以接触线与啮合极限点N1的距离为自变量,不同相位的啮合齿宽b可按如下方式计算[24]：

(2)

式中:s-N1B2为关于时间的函数,s-N1B2=rb1ωt。设(s-N1B2)/tanβb=sa。

双渐开线齿轮接触线在基圆柱上的展开图如图2所示。

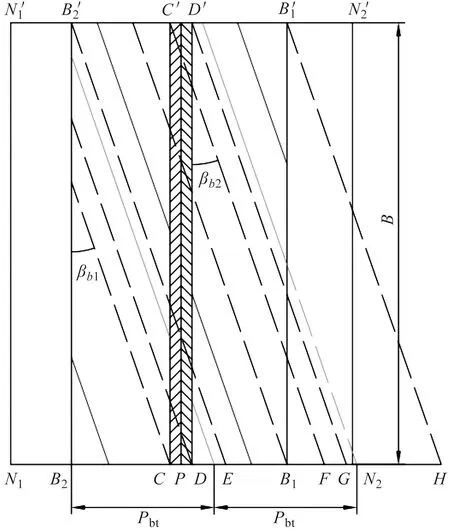
图2 接触线在基圆柱上展开图

图2中,阴影区域为齿腰分阶位置不参与啮合的区域,造成接触线长度的损失。其中,βb1、βb2为基圆螺旋角,Pbt为端面基节。

当双渐开线齿轮端面重合度大于轴向重合度时,接触线长度可表示为:

(3)

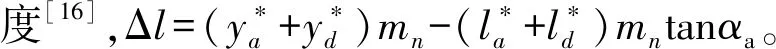
双渐开线齿轮副基本参数如表1所示。

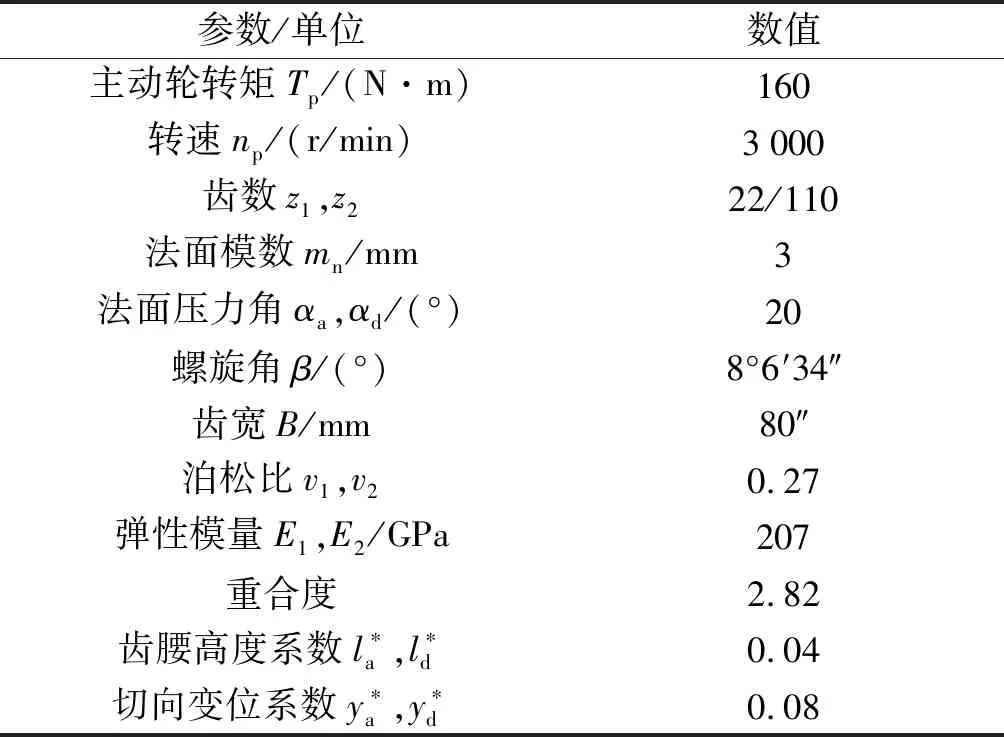
表1 齿轮主要参数

笔者对表1所提供的双渐开线齿轮参数进行时变接触线长度变化分析,如图3所示。

图3 时变接触线长度变化图

图3中,上方为啮合过程中接触线总长度,下方为一个啮合周期内参与啮合的各条接触线长度,由于重合度不为整数,齿轮参与啮合轮齿对数随啮合时间周期性变化,接触线总长度同样随啮合时间稳定波动。

2 双渐开线齿轮时变接触线载荷分布

2.1 载荷分布模型的建立

笔者采用“分段法”,将接触线平均分成m等份,对每一小段接触线上的相关特性进行研究。

分段模型和几何参数如图4所示。

图4 轮齿接触线划分和几何参数

图4中,每段接触线上的载荷沿接触线方向均匀分布;每段接触线之间相互独立。

假设轮齿为齿根侧固定的悬臂梁,根据Timoshenko梁理论,每段接触线啮合过程中的轮齿总势能u包括弯曲势能ux、剪切势能un和轴向压缩势能us,u表示为:

u=ux+un+us

(4)

各势能分量表达式为[7]：

(5)

式中:E为齿轮材料弯曲弹性模量,MPa;G为剪切弹性模量,MPa;yc,yp为接触点和齿根圆到x轴的距离,作为势能积分的上下限;y为积分限内单位微元到O点的距离;e(y)为该微元的宽度。

由于剪应力在截面内非均匀分布,根据Colignon定理,笔者利用修正因子Cs对剪切势能进行修正,对于矩形截面,取Cs=1.2[21]。

αc是渐开线齿廓位置的函数,其表达式为:

(6)

式中:ξc为啮合点位置参数,受轮齿齿廓和瞬时啮合位置的影响。

啮合点位置参数ξc表达式为[8]：

(7)

式中:z为齿数。

基圆半径与单个轮齿的齿廓交点所成圆心角γb为[22-23]：

(8)

式中:χ为变位系数;αt为端面压力角。

势能积分上限yc为:

(9)

式中:γc为接触点处e(y)对应的圆心角。

由双渐开线齿轮的端面齿廓方程[24]25可求得势能积分下限yp和微元宽e(y),双渐开线齿轮齿根过渡曲线方程为:

(10)

则势能积分下限yp和微元宽e(y)为:

e(y)=2xs

(11)

yp=ys

(12)

每段接触线啮合产生的轮齿总弹性势能包括主动轮弹性势能u1、从动轮弹性势能u2、接触弹性势能uc和齿轮基体势能uf。双渐开线齿轮副在标准安装条件下,接触线都位于啮合平面内。

主、从动轮的啮合点位置参数ξ1和ξ2之间的关系为[10]：

(13)

式中:z1,z2为主、从动轮齿数;α′t为端面啮合角。

对于主、从动轮材料相同的齿轮副,赫兹接触刚度为[25]：

(14)

式中:v为泊松比;E为齿轮材料弯曲弹性模量,MPa。

则赫兹接触弹性势能为:

(15)

其中:cu=2(1-v)2/(πE),当齿轮材料一定时,cu为常数。

齿轮基体刚度为:

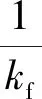
(16)

其中的参数详见文献[26]。

则齿轮基体弹性势能为:

(17)

定义函数:

(18)

则式(11)中的弹性势能u可表示为:

(19)

又因啮合点的向径yc与啮合点位置参数ξc一一对应,则式(19)可转化为:

(20)

一段接触线啮合过程中轮齿的总弹性势能up为:

(21)

则每条接触线啮合过程中轮齿的总弹性势能ut为:

(22)

式中:n为瞬时接触线的数量;ni为齿轮分段法涉及的接触线段的数量;uij为第i条接触线涉及的接触线段j啮合产生的弹性势能;Fij为对应的载荷。

载荷平衡关系为:

(23)

式中:Ft为斜齿轮副的法向总载荷;Pin为输入功率。

最小弹性势能原理表述为系统在真实的位移场内弹性势能取最小值,笔者采用拉格朗日乘子法求解。拉格朗日函数为:

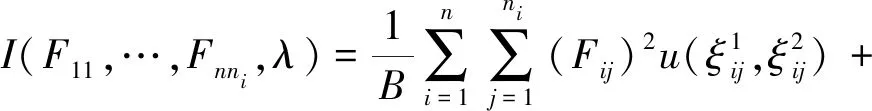
(24)

式中:λ为拉格朗日乘子。

联立约束条件及原函数,分别对F11,…Fij…,λ求导,在极值点处有:

(25)

求解上式可得第i条接触线上第j段的载荷为:

(26)

弹性势能是位置函数,取决于轮齿的瞬时啮合位置[27]。

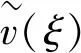
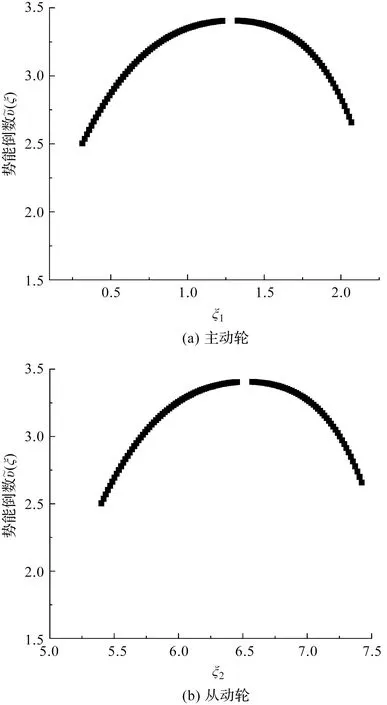
图5 齿廓参数与势能倒数的关系

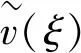
每条接触线上的载荷等于分段法各段接触线载荷之和,则齿间载荷分配率可表示为:

(27)

2.2 载荷分布模型的数值计算

载荷分布流程如图6所示。

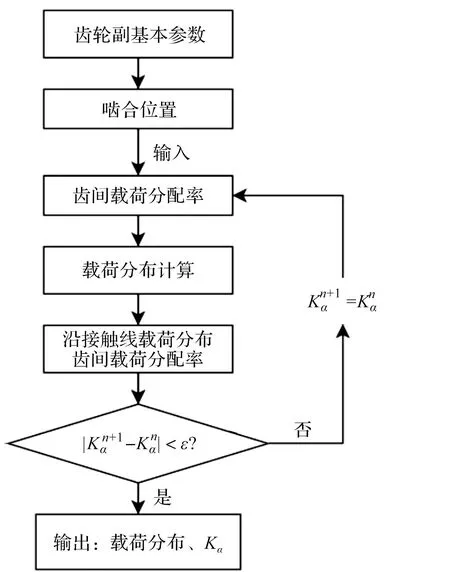
图6 载荷分布计算流程图

笔者通过迭代计算求解轮齿间的载荷分布,将啮合周期离散为若干个啮合时刻,通过式(3)获得瞬时接触线的啮合位置参数ξc;选定某一啮合时刻进行数值计算。

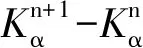
对若干个离散的啮合位置进行迭代计算,获得齿面离散的载荷分布,然后利用插值算法,获得齿面连续的载荷分布。阈值ε取为0.01[10]。

笔者通过表1所提供的齿轮副参数进行数值计算,并将载荷进行归一化处理,得到的双渐开线齿轮沿接触线的载荷分布,如图7所示。

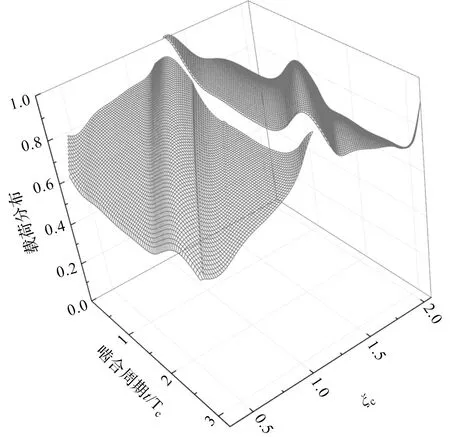
图7 齿面载荷分布

图7中,齿腰分阶区域载荷值较大,随着啮合的进行,沿接触线的载荷分布出现两处峰值。

结合图3可知,峰值的产生是因为此处双渐开线齿轮由三对齿啮合过渡为两对齿啮合,峰值对应两对齿啮合中的两条接触线,此时沿接触线载荷在整个啮合周期中达到最大值。

由载荷的变化规律可知,双渐开线齿轮沿接触线的载荷分布受瞬时啮合位置、接触线长度以及总接触线长度的影响,其最小值为最大值的61.6%,载荷分布较为均匀,未发生明显的突变。

2.3 载荷分布模型的验证

网格划分如图8所示。

图8 双渐开线齿轮有限元网格划分示意图

为验证载荷分布模型的准确性,笔者将数学模型与有限元模型进行对比。

笔者采用文献[24]24-25提供的齿面方程,在SolidWorks中建立精确的齿轮几何模型;为获得较好的收敛性和仿真结果,利用HyperMesh进行高精度网格划分,详细的边界设置由文献[19]给出。

笔者利用数值计算法和有限元仿真法分别计算接触线的齿间载荷分布,结果如图9所示。

图9 齿间载荷分布

图9(a)取图1中啮合时刻,3条接触线分别为L1、L2和L3;整个啮合周期离散为20条接触线,载荷分配率如图9(b)。

两种方法的计算结果差距很小,有限元法获得的L2的载荷分配率大于数值计算法所得的载荷分配率,存在差异的原因与数值计算时接触线段的相互独立和双渐开线齿轮在齿腰处分阶有关。

首先,数值计算过程中,分段法忽略了接触线段之间的关系,每段接触线参与啮合的同一啮合点位置参数ξc的刚度均相同,而有限元模型将整个双渐开线齿轮视为一个整体,这导致齿宽中间齿轮片的刚度大于齿宽两端齿轮片的刚度;其次,双渐开线齿轮由于在齿腰附近分阶,齿根渐开线ξc发生跳跃,并明显反映在有限元仿真结果中,而ξc的跳跃在数值计算的方法中对结果的影响并不明显。

笔者取有限元仿真结果中的节点载荷,沿齿宽方向均匀分配给相邻的两个单元体,利用MATLAB进行插值计算,获得齿宽方向连续的载荷分布[28-30]。

沿接触线方向归一化的载荷分布如图10所示。

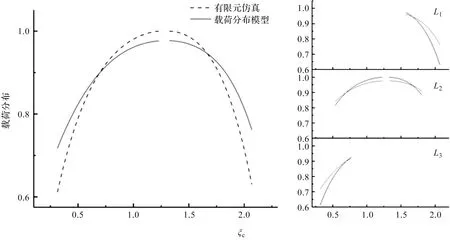
图10 接触线载荷分布

图10中,左侧为完整的啮合点位置参数与载荷的分布关系,右侧为瞬时啮合时刻3条接触线的载荷分布,两种方法的载荷分布趋势基本吻合。归一化处理后载荷分布模型的载荷最大值为0.977,两者之间的误差低于2.3%,越靠近节线,载荷越大。

综上所述,笔者建立的基于最小势能原理的载荷分布模型与有限元仿真基本吻合,验证了载荷分布模型的精确性及合理性。

3 双渐开线齿轮与普通渐开线齿轮载荷分布对比

笔者取同一基本参数下的普通渐开线齿轮,并采用ISO6336-1:2006(E)[1]对其求解,计算公式如下:

(28)

其中的具体参数见ISO6336-1:2006(E)。

双渐开线齿轮与普通渐开线齿轮载荷分布模型以及ISO6336-1:2006(E)方法下的载荷分配率对比,如图11所示。

图11 DIG与CIG载荷分布对比

从图11可见:双渐开线齿轮载荷分配率平均值为37.97%,普通渐开线齿轮为35.1%,双渐开线齿轮载荷分配率波动幅度较小,优于普通渐开线齿轮。在完整的啮合周期中,双渐开线齿轮载荷分配率最大值为0.57,最小值为0.037;普通渐开线载荷分配率最大值为0.63,最小值为0.023;双渐开线齿轮载荷分配率最大值为最小值的6.5%,普通渐开线齿轮仅为3.6%;双渐开线齿轮载荷分布较普通渐开线齿轮载荷分布均匀,无大范围明显波动和突变。

4 载荷分布模型影响因素分析

4.1 输入扭矩对载荷分布的影响因素分析

笔者取输入扭矩T=100 N·m、160 N·m、300 N·m,齿宽B=80 mm,在其他参数相同的情况下,得到了不同输入扭矩沿齿面的载荷分布,如图12所示。

图12 不同输入扭矩的载荷分布

从图12(a)可以看出:当输入扭矩增加时,深色阴影面积明显增加,且载荷等高线密度逐渐增大,且最大载荷也明显增加,但总的接触轨迹和载荷分布规律基本保持不变。

从图12(b)可以看出:当输入扭矩较小时,双渐开线齿轮载荷分配较为均匀,随着输入扭矩的增加,双渐开线齿轮载荷分配产生波动,且在中后期发生突变,这是由于此时齿根渐开线应力最大值处脱离啮合,导致接触线承载载荷发生突变。

4.2 齿宽对载荷分布的影响因素分析

笔者分别取齿宽B=40 mm、80 mm、120 mm,T=160 N·m,在其他参数相同情况下,探究齿宽对双渐开线齿轮载荷分布的影响。

啮合周期内的载荷分配率如图13所示。

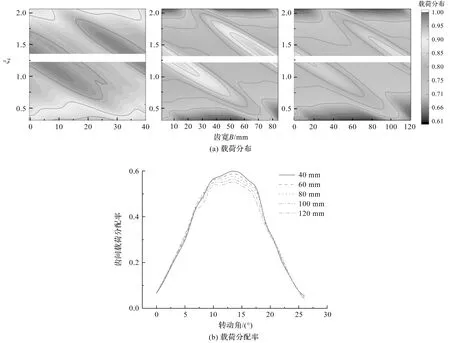
图13 不同齿宽的载荷分布

由图13(a)可知:齿宽增加,相同啮合位置参数ξc下的载荷波动减小,但沿接触线的载荷波动增大。

由图13(b)可知:载荷集中于接触线中心位置。结合式(20)可知,随着齿宽的增加,齿轮在啮合过程中的弹性势能降低,单位载荷减小;同时齿宽系数增大,载荷沿接触线分布不均匀的程度增大。

上述分析表明,过大的齿宽会出现载荷集中现象,导致齿轮产生振动和噪声。

5 结束语

笔者对双渐开线齿轮时变接触线长度进行了分析,并采用“分段法”将双渐开线齿轮接触线等分为若干段,基于最小势能原理建立了双渐开线齿轮载荷分布模型;利用载荷分布模型、有限元模型与ISO6336-1:2006(E)进行了比对分析,验证了载荷分布模型的准确性;将双渐开线齿轮与普通渐开线齿轮的载荷分布进行了对比分析,并研究了输入扭矩、齿宽对双渐开线齿轮载荷分布的影响。

研究得出以下结论:

1)双渐开线齿轮沿接触线方向载荷分布不均,最大值位于节线附近,接触线两端载荷逐渐减小,同一基本参数下,双渐开线齿轮载荷分配率平均值为37.97%,普通渐开线齿轮为35.1%,双渐开线齿轮相较于普通渐开线齿轮载荷分布波动幅度略小,优于普通渐开线齿轮,但差距不大;

2)双渐开线最大接触应力值通常出现在下齿面靠近齿腰位置,随着输入扭矩的增加,导致载荷分配率在啮合后期发生突变,沿接触线方向的载荷在节线附近发生突变;

3)齿宽增加,双渐开线齿轮沿接触线载荷分布的不均匀程度增加,过大的齿宽会出现载荷集中现象,导致齿轮产生振动和噪声。

笔者后续的研究方向为:1)将结合齿面粗糙度,建立动力学模型,在求载荷分布模型的基础之上,探究双渐开线齿轮齿面动态载荷分布特性;2)基于齿轮动载荷分布特性进行齿轮接触疲劳的研究。