某型复杂工程机械变速箱体复合工艺约束机加工线平衡研究*

金初云,胡俊逸,2*,陈 勇,王一鸿

(1.浙江交通职业技术学院 轨道交通学院,浙江 杭州 311112;2.西南交通大学 机械工程学院,四川 成都 610031;3.浙江工业大学 机械工程学院,浙江 杭州 310023)

0 引 言

当前以加工中心、车铣复合、多轴联动等高端制造设备为主的柔性生产线可胜任绝大多数复杂零件的机械加工工序。而在多台柔性机床构成的生产线中,往往存在耗时较长的瓶颈工序。承担瓶颈工序的机床决定了整条生产线的节拍,并影响了高端柔性生产线的产能发挥[1-2]。因此,如何平衡分配零件的加工任务至多台机床中,使得每台机床所分配的加工任务平均化,消除瓶颈工序,一直是困扰加工制造业的难题之一。

针对典型复杂零件的工序平衡化分配问题展开研究具有重要的意义。

制造类生产线可分为装配/拆卸工艺类、机械加工类以及石化冶金流程工业类三种。对于装配/拆卸线平衡问题已有学者进行了较多研究。张则强等人[3-7]将智能优化算法应用于装配/拆卸线平衡研究领域,且获得较好的成效。而当前针对机械加工类的生产线问题,往往集中于加工任务所形成的最短有效任务链的研究,如文笑雨等人[8]和张雷等人[9]分别研究了最短机加工任务链构建问题,以及在此基础上考虑减少换刀次数,机床工位翻转次数等附加加工辅助过程的复杂问题。通过OSMAN H等人[10]1350和张恒等人[11]2504的研究成果得知,机加工生产线平衡问题(transfer line balancing problem,TLBP)是在加工任务链规划基础上的后续优化。

针对该问题,国外有较少的学者进行了研究。BORISOVSKY P等人[12]研究了包含紧密和禁忌约束以及任务切换时间的机加工生产线平衡问题;但BORISOVSKY P等人未考虑机床类型需求。ESSAFI M等人[13]以最小化工位数量为优化目标,进行了机加工生产线平衡问题的研究;ESSAFI M等人虽考虑了机床类型需求,但未考虑紧密型和“或”型约束条件。OSMAN H等人[10]1345考虑了刀具需求和机床类型需求,以最小化加工辅助时间(如换刀时间、等待时间)为优化目标,同时将加工任务均衡的分配到各个工位中,并采用一种蚁群算法进行了求解;但OSMAN H等人未考虑任务之间的紧密型和“或”型约束。

国内也有学者对此问题进行了研究,已取得一定的成果。李爱平等人[14]以零件装夹定位方案为加工要素的聚类约束,并考虑换刀、转位等加工辅助要素,采用蚁群算法进行了优化改进;但未考虑“或”型约束。章正伟[15]提出了更贴近实际情况的“或”型约束以完善现有的工艺约束矩阵,同时也采用蚁群算法进行了求解;但未考虑机床类型需求。张恒等人[11]2501针对零件族类提出了一种混流零件生产线平衡问题的改进遗传算法;但未考虑聚类、“或”型等实际约束。刘雪梅等人[16]采用改进遗传算法研究了零件生产线平衡多目标优化问题;但未考虑“或”型约束。胡俊逸等人[17]首次提出了首尾加工辅助要素的概念,并采用蚁群算法求解了综合考虑紧密型和“或”型约束的机加工生产线平衡问题;但其提出的数学模型并未考虑加工任务的机床类型需求。

现有方法以定位装夹为聚类准则,以加工约束矩阵为加工任务先后约束关系,以蚁群或遗传算法求解机加工生产线平衡问题。但在约束条件的设置角度,或仅考虑换刀、转位等辅助要素,或仅考虑增加“或”型约束来改善任务约束矩阵,未能将两者综合;且未综合考虑加工方位、机床类型、紧密约束等多种约束条件,因此限制了优化结果在实践中的应用。

笔者在引入文献[14]考虑换刀辅助要素,文献[15]的“或”型约束条件基础上,同时考虑机床类型需求、紧密约束、加工方位约束,以节拍和平衡率为优化目标,研究一种基于可行任务选集的粒子群算法来满足多种复杂的约束条件,同时以某型复杂箱体为算例,验证该算法的实用性。

1 机加工生产线平衡工艺约束定义

1.1 约束关系矩阵

在机械加工中,完成一个尺寸要素的加工往往需要多个工步,如粗加工、半精加工、精加工等。

为简化问题求解难度,笔者将某一尺寸要素的连贯性加工工步整合为一个工步(将粗刀换精刀等辅助时间统计在内),同时这也符合实际操作中钻铰孔、钻镗孔、孔钻攻丝、粗精铣面、钻深长孔工步组合等情形[15],也符合现今复合丝锥、钻铰刀等复合刀具大量应用的情形。

在此基础上,可提出所有加工要素之间的工艺先后约束关系矩阵如下:

(1)

若尺寸要素i加工完毕之后,尺寸要素j才允许被加工,则aij=1;若尺寸要素i或尺寸要素k任意一个加工完毕之后,尺寸要素j均可允许被加工,则aij=akj=2,即“或”型约束[16],若i或k之一被加工,则另一要素与j的先后约束关系失效,可设置为-1;若尺寸要素i加工完毕之后,必须立即加工尺寸要素j,则aij=-2,即i与j为紧密约束;若尺寸要素i与尺寸要素j之间并无任何先后约束关系,则aij=0。

综上所述,aij的可能取值如下:aij=(-2,-1,0,1,2)。

相比于文献[1,9-14],增加“或”型约束后,其改善了先后约束关系矩阵,为任务编排提供更多可能[15];相比于文献[15],其增加紧密约束后使得在编排如一面两销等多定位基准要素时,使之优先安排在同一工位中,更符合先加工定位基准/尺寸评价基准要素,后加工被评价尺寸要素的工艺编排原则。

同时,增加考虑了加工方位约束、刀具类型需求约束、机床类型需求约束,也更加符合机加工生产线现场实际情形。

1.2 机加工生产线平衡数学模型

某零件所有加工任务之间的先后顺序约束有向图如图1所示。

图1 复合约束加工工艺有向图

圆圈内的数字表示任务序号,两个任务之间的先后顺序约束用实线箭头;两个任务之间的“或”型约束采用虚线箭头;用虚线框将紧密约束要素包围。如:任务1和2为正常先后关系约束,则a12=1;任务8和4、8和5为“或”型约束关系,则a58=a48=2;任务5和7为紧密约束关系,则a57=-2;任务2和3之间没有任何约束关系,则a12=0。

图1表示的某零件的机加工产线示意图如图2所示。

图2 一种满足图1的5工位工艺编排方案

图2表示机加工产线由5个工位组成,每个工位包含多个加工要素,被加工零件在工位中在一次定位装夹后完成本工位所有加工要素的加工任务,零件依次在后续工位中流转,直到完成所有加工内容。箭头表示加工工件在不同工位之中的流动顺序;括号表示将多个任务安排在同一个工位中;工位1和工位3都仅安排了一个加工任务,其余工位均安排了多个加工任务。在图2所示的编排方案中,若假设在任务5和任务7未安排时就优先安排任务8在工位4,也是可行的,因当任务4安排之后,a48=a58=-1,任务8的约束关系被释放,因此任务8可自由分配。

因任务2和任务3所用加工刀具不同,则要在两个任务之间插入换刀时间;且还需满足加工方位限制。

该零件满足图1和图2约束关系的工艺编排甘特图如图3所示。

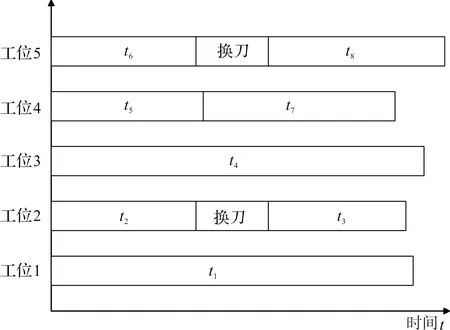
图3 满足图1和图2约束的5工位工艺编排甘特图

图3表示同一个工件依次在不同工位中按顺序流转,每个工位的加工时间由当前工位对应的加工任务i的加工时间ti来决定,且当同个工位包含多个加工任务时,还需考虑不同加工任务所需刀具差异所带来的换刀时间。图2所示的编排方案仅是一种可能,任何满足矩阵约束A的编排方案均具备可行性。而在实际情形中,每个工位的最长操作时间即节拍时间C是影响加工效率的最关键因素,是不可忽视的约束条件。

因此,有必要通过数学模型对多种约束条件的定义来约束算法的设计,从而保证任务编排过程可满足多种约束条件,实现编排方案的可行性。

含换刀、生产准备任务等辅助工步的机加工生产线的平衡问题数学模型如下所示:

表示要素只能被分配到某一个工位,不可重复分配,公式如下:

Sx∩Sy=Фx≠yx,y=1,2,…,m

(2)

式中:Sx,Sy分别为工位x、工位y;Ф为空集;m为工位数。

表示所有要素均要归属于某一工位,不可出现遗漏,公式如下:

(3)

式中:Sk为工位k。

表示每个工位中加工要素累计时间的求和项与换刀累计时间(ck×ph)之和应小于节拍时间C,公式如下:

(4)

式中:Tk为工位k的累计时间总和;ck为工位内换刀次数;ph为平均换刀时间。

表示要素分配过程的常规先后约束如下:

∀i∈Sx,j∈Sy若aij=1则x≤y

(5)

表示“或”型约束如下:

∀i∈Sx,j∈Sy若aij=2则x≤y

(6)

表示紧密约束如下:

∀i∈Sx,j∈Sy若aij=-2则x=y

(7)

表示任务的加工方位约束如下:

∀i,j∈Sx,oi=oj

(8)

表示任务的加工机床类型约束如下:

∀i,j∈Sx,ei=ej

(9)

表示工位要素集合如下:

Sk={i|i∈Sk}

(10)

表示全体要素集合如下:

Ω={1,2,…,n}

(11)

式中:n为要素总数。

平衡率如下:

(12)

式中:LB为平衡率。

最大化平衡率目标函数如下:

F1=Max(LB)

(13)

最小化工位数量目标函数如下:

F2=Min(m)

(14)

最小化换刀次数目标函数如下:

(15)

笔者利用以上模型对文献[15]中有关“或”型约束释放后的情形进行了补充定义,同时相对文献[17]增加了机床类型约束和加工方位约束,这样更加复合实际工艺编排的多种约束类型。

但在模型中,节拍时间C将影响任务在不同工位中的分配结果,同时当改变两个任务前后顺序时(假设改变后仍然满足矩阵A的约束),由于任务所需刀具型号的差异,又将引起换刀时间的变化。

因该问题是逻辑较为复杂的非线性问题,更适合采用启发式算法求解。

2 机加工生产线平衡粒子群算法

2.1 含启发式任务筛选规则粒子群算法流程

常用的元启发式算法有遗传算法、粒子群算法等。笔者研究的任务排序问题是具有较多强互关性的约束条件,若采用遗传算法的随机交叉和变异算子,任务在序列中(各工位之间)随机位移将破坏任务所属机床类型、加工方位等约束条件,易导致不可行解的产生,限制算法进化效率。若在构造加工任务序列过程中通过改变任务的被选概率的方法进行迭代优化,且避免任务序列间随机交叉对可行序列的随机破坏,则可保证任务序列的可行性。

因此,采用基于任务选择权值的元启发式算法具有更多的便利,粒子群算法成为求解该问题的优选。

相对于文献[15]和[17],笔者分别增加了刀具类型和机床类型约束,兼顾先后顺序、“或”型约束和紧密约束特殊情况,同时考虑换刀增加的工位总耗时。

整体算法流程图如图4所示。

图4中,在构建加工任务链的每一步搜索过程中,需综合考虑以上约束条件,建立待搜索要素集合。因此,构建时间约束集合生成模块、机床类型约束模块、加工方位约束集合生成模块、刀具约束集合生成模块、紧密约束集合生成模块,将其作为启发式规则以满足约束条件。

随着国家政策的调整、对西部地区的倾斜发展和对“三农”投入力度的加大，少数民族地区农业产业结构调整取得了一定成效，农村经济得到快速发展，农民的生活水平显著提高。但是，农民补贴增加、农民增收减负，而农产品结构、农业产业结构和区域布局调整不明显。虽然共和县在蔬菜产业结构调整中取得了一定成效，但由于地理、历史、文化等诸多因素影响，仍然存在着一些问题。

2.2 启发式备选任务集生成规则

相对于文献[15]和文献[17],改进后的流程保证所生成的加工任务链满足各种复杂约束条件。

具体步骤为:利用粒子群算法构成要素序列,在第s步均将生成候选任务集;然后采用粒子群中粒子位置向量作为待加工任务的被选择权重的规则来选择待加工任务,直到完成n个任务的选择,形成完整的任务加工链。

1)时间约束规则。综合考虑“或”型约束,以及常规先后关系约束、节拍时间约束;判断某任务j是否可加入初始可供选择任务集合的流程为:

②设当前工作站k的安排任务完成时间为ttemp,则根据节拍时间C约束初步筛选得到以下候选任务集合Ds={j|ttemp+tj≤C};

2)机床约束规则。综合考虑当前工作站k的机床型号,与待分配任务j所适用的机床型号的差异,从而考虑机床类型匹配,对1)中的时间约束集Ds做进一步筛选:

3)方位约束规则。综合考虑当前工作站k的机床加工任务时的零件方位,与待分配任务j所适用的加工方位的差异,从而考虑加工方位一致性,对1)中的时间约束集Ds做进一步筛选:

4)刀具约束规则。综合考虑当前工作站k的刀塔刀具,与待分配任务j所用刀具的差异,从而考虑换刀时间,对1)中的时间约束集Ds做进一步筛选:

①若j与当前工作站中前一任务所需刀具相同,则需不考虑刀具准备时间ph;

③综合以上情况,得到符合刀具约束的集合Ts;

5)在以上步骤基础上,进一步考虑紧密约束条件,生成紧密约束集合Js;并采用基于任务所对应粒子位置权重进行任务的最终选择。

2.3 粒子群算法的任务选择过程

粒子群优化(PSO)算法采用粒子位置权值赋予待搜索变量,采用速度向量赋予变量变化趋势,搜索过程简单高效,在科学研究和工程应用方面比较有优势[18-21]。

笔者保留标准粒子群算法核心算子,以粒子位置权值赋予任务选择权值,以粒子速度赋予任务选择权值的变化趋势,从而将粒子群算法较好地融入问题求解过程,以启发式备选任务集生成规则约束任务链,从而保证其可行性。

(16)

(17)

3 某箱体机加工工艺平衡编排案例

3.1 某型工程机械变速箱体的评价基准分析

某型工程机械变速箱体[17]的关键评价基准要素示意图如图5所示。

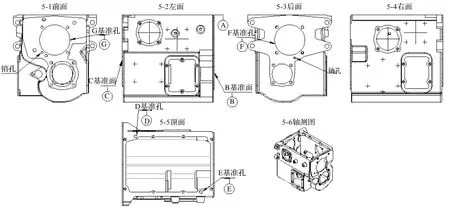
图5 某型箱体关键评价基准三视图

图5中,B、G基准以A、D、E基准为评价要素,C、F基准以B、G基准为评价要素;由此可知,A、D、E基准最为重要,因安排在首道工序加工,且为保证A、D、E之间相互位置精度,应设置为紧密约束集(由一次装夹定位后在同一个工位中一起加工,因此由机床自身精度来保证A、D、E之间的相互位置精度);同理,B、G基准也必须安排在同一道工序加工,因此也设置为紧密约束。

因C、F基准为自身所在平面上加工要素的评价基准,因此,以上情况同样适用于基准C、F。

3.2 箱体加工工艺分析

图5所示箱体的73个机加工要素,分别归属于零件的顶面、左右侧面、前面、后面。由于核心评价基准A、D、E位于顶面,因此在安排工序时将A、D、E的加工放在首位。

由于B、G基准位于零件的前面,且以A、D、E基准为评价要素,因此可以A、D、E基准作为定位基准来加工B、G基准;同理,C、F基准既可由A、B、E也可由B、G基准作为定位基准来加工。

73个加工任务之间的优先顺序约束关系如图6所示。

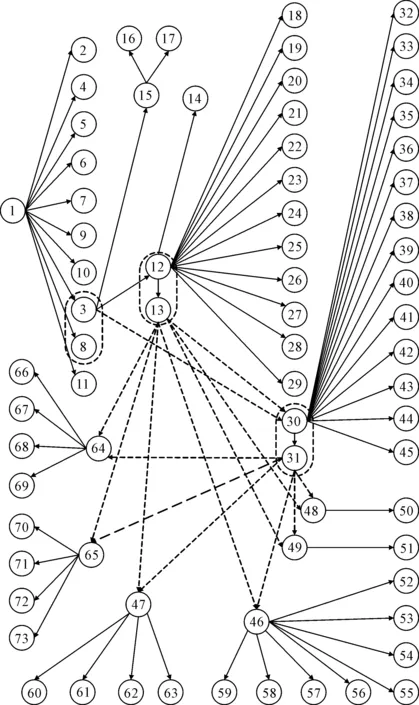
图6 加工约束关系图

由图6可以看出:由于各基准之间的加工先后顺序约束,导致与以上基准归集于同一加工方位的各加工任务之间便自然继承了各基准之间的先后约束关系;同时,一般可将位于被加工面上的所有加工孔要素归集为此加工面的紧后加工任务;根据以上两点原则,可将此箱体零件的73个被加工要素编制出加工顺序约束有向图。如任务3和8、12和13、30和31之间为紧密型约束,则这些成对任务必须安排在同一个工位中完成。

任务3和13为任务30的“或”型约束,任务13和31为任务46、任务47、任务48、任务49、任务64、任务65的“或”型约束,则只要任务13和31之间任何一个完成加工,后续的任务46～49、64、65均可被安排。

每个任务的加工方位约束和加工机床类型约束如表1所示。

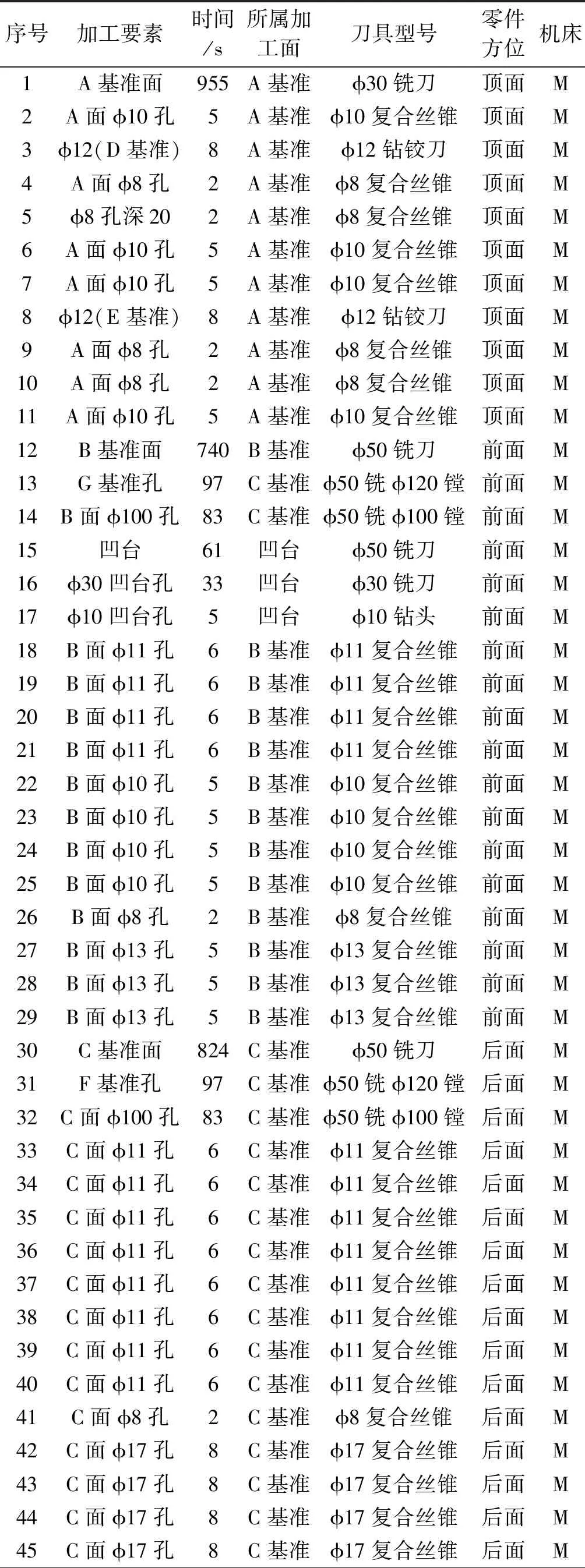
表1 任务操作工序及时间

在安排表1中的任务时,必须保证同个工位中的所有任务具有相同的机床类型和加工方位类型。

4 箱体加工生产线规划

笔者以年产量1.7×104台～2.0×104台为目标(工作周:50周,每周工作12班次,每班次8 h计算),可得周产能目标为330套～390套,按每周6天两班倒可得每班产能为27套～33套。可将节拍时间(C)预设为17 min～20 min,针对此TLBP问题,将预定节拍时间细化为以10 s为级差的等差数列,采用粒子群算法进行运算,设置蚂蚁数目10,运算代数100。m为计算得到的工位数目(单位:个),LB为平衡率。表1为73个加工任务的工艺需求表。相对于文献[17]增加了机床需求约束,M表示高精度加工中心,Z表示普通精度加工中心。

采用粒子群算法所得优化方案结果如表2所示。

表2 采用优化算法各节拍测试结果对比

从表2中可得:当节拍时间为1 120 s时,整体加工线的平衡率最高,达到94.66%。表2中方案均能满足产能需求,但当节拍时间缩短为1 110 s或1 100 s之后,单班产能仅增加0.2台～0.5台,但加工线平衡率将下降15.07%～25.82%,造成设备和人员资源的极大浪费,且因增设设备台数,增加资产投入和人员成本,故节拍1 120 s为优选方案。

人工排产方案所得平衡率、工位数、换刀时间随预设节拍时间的变化如表3所示。

表3 人工排产各节拍结果对比

从表3中可知:人工排产主要依靠经验而为,无法具备算法高速计算多次迭代收敛的优异性能。因此,人工排产效果较差,其最优的平衡率仅为78.88%。

粒子群算法所求得最高平衡率方案(节拍时间为1 120 s,平衡率为94.66%)的具体任务分配表如表4所示。

表4 粒子群算法节拍1 120 s方案优化结果

表4中,笔者对每个工位中的每个任务加工起始时刻和加工完成时刻进行排列,同时提供该工位的换刀次数/换刀时间信息。

人工排产和优化算法排产所得工位数量对比图如图7所示。

图7 人工排产与优化算法排产工位数量对比

人工排产和优化算法排产所得平衡率对比图如图8所示。

图8 人工排产与优化算法排产平衡率对比

人工排产和优化算法排产所得换刀次数对比图如图9所示。

图9 人工排产与优化算法排产换刀次数对比

对比图7～图9可知:由于人工排产仅依靠经验,未能充分综合考虑换刀、加工方位、平衡率、工位数量等复杂约束条件的影响,在绝大多数情形下工位数量、整线平衡率和换刀次数三个关键指标均劣于优化算法的排产结果。

且全局较优解也由优化算法得到,因此也说明该优化算法能辅助工艺规划工程师工作的同时,且能得到综合指标更优的机加工生产线规划方案。

由表4所得加工任务编排甘特图如图10所示。

图10 节拍时间1 120 s任务编排甘特图

与图10零件属同族零件的相同节拍下任务安排甘特图如图11所示。

图11 简化版零件节拍时间1 120 s任务编排甘特图

图10中,结尾任务(finally task)为去毛刺及最终检验任务。甘特图由算法生成,浅色任务表示加工该任务,需首先进行换刀作业,且浅色任务时间增加了平均换刀时间;深色任务表示不需要换刀作业,因此不含换刀时间。

从图10、图11可知:紧密约束任务3和8、12和13、30和31均成对的安排在工位1、工位2、工位3中,满足紧密约束条件;工位1中任务均满足机床类型M和加工方位为顶面的约束;工位2中任务均满足机床类型M和加工方位为前面的约束;工位3中任务均满足机床类型M和加工方位为后面的约束;工位4中任务均满足机床类型Z和加工方位为右侧的约束;工位5中任务均满足机床类型Z和加工方位为左侧的约束。

综上所述,图中任务编排均满足先后约束关系约束、加工方位约束、刀具约束、机床需求约束以及辅助任务约束,体现优化算法的实用性。

以上说明,笔者采用启发式备选任务集生成规则对标准粒子群算法进行改进后,能够很好地求解所研究的问题。

5 算法应用探讨

针对生产柔性问题,笔者以同族类零件和不同族零件两个角度进行分析:

1)基于同一毛坯的同族类零件加工柔性分析。若本算例为包含完整机加工尺寸的零件,本族内其他零件尺寸区别仅限于加工尺寸数量的减少,且减少尺寸一般不影响留存尺寸的先后约束关系;则用于加工当前最全面尺寸零件的生产线构型和机床刀具方案具备优异的生产柔性,只需通过在每工位的机床中预留同族内不同零件的删减对应尺寸版数控代码,就可完美无缝地切换生产同族内其他类型零件。

2)基于不同类型毛坯的异族类零件加工柔性分析。在采用优化算法的基础上,通过借鉴文献[11]中为两种不同类型箱体零件分别预设多种构型的平衡方案,进一步寻找两组方案中具备相同构型的平衡方案,作为柔性混流生产线的设计方案。也可实现基于构型不变的柔性生产线。但这种柔性生产线,由于两种箱体毛坯和加工尺寸存在较大差异,在切换线时,必然要更换工装和部分刀具,需要调整的时间相较于第一种柔性生产线会更多。

以上文所述的第1)种生产柔性为例,假设同族类零件相比于完整版零件减少任务42和62。只需将对应工位被简化的任务删除即可实现快速柔性切换目的(换刀时间需根据删除后前后任务刀具差异情形增减)。如图11所示为调整后的同族类简化加工版零件产线甘特图,将工位3中的42号任务,以及工位4中的62号任务删除后所得。

由于被删除的42号任务所用刀具与原有甘特图中前任务39所需刀具不同,而39号却和原甘特图中42号后面的任务33所用刀具相同,因此删除42号任务后,任务39和33之间不需要换刀作业(33号任务在新甘特图中减去换刀时间后变为深色),因此切换线过程极为简便。由于被删除的62号任务在原甘特图中的前后任务所用刀具不同,因此删除62号之后原甘特图中54号任务须增加换刀时间,54号任务在新甘特图中变为浅色。

针对上文第2)种异族类零件之间的生产柔性,限于篇幅暂未提供详细的算例说明。

综上所述,笔者所提出的平衡优化算法,具备一定的生产柔性,可为多种类箱体零件的柔性生产线规划设计提供解决方案。

6 结束语

笔者研究了包含换刀、加工辅助、“或”和“紧密”约束、刀具需求、机床需求等复杂约束条件综合作用下的机加工生产线平衡问题,设计了一种粒子群算法,加工任务集的多重筛选机制满足以上复杂约束条件,通过粒子群基于位置权重的搜索策略进行了加工任务链的构建,并设计了甘特图自动生成模块;对某型复杂箱体的加工工艺案例进行了细致分析,分析其定位基准、评价基准并设计了其加工任务的优先顺序图,建立了合理的工艺约束条件;将该案例带入粒子群算法求解,验证了该算法的有效性和高效性。

结论如下:

1)采用含有多重筛选机制的粒子群算法,对复杂零部件的机加工生产线规划问题能够得到多组高于90%平衡率解决方案;以节拍时间为1 120 s的优化方案为优选方案,其平衡率为94.66%,换刀次数仅为39次,具有兼顾成本和效率的综合优势;

2)能够在加工工艺规划和产能分析阶段进行详细的工位任务设计和生产设备需求的分析;

3)具备一定的生产柔性,为制造业管理者提供更智能化的决策分析方法。

未来,笔者将进一步对更多复杂的实际约束条件进行研究,如机床加工参数限制条件、人员需求约束,从而为生产决策提供更精细的解决方案。