EHDE和WHO-SVM模型在齿轮箱故障诊断中的应用*

2024-04-24马晓娜周海超

机电工程 2024年4期

马晓娜,周海超

(1.郑州信息工程职业学院艺术与教育学院,河南郑州 450000;2.武汉科技大学机械自动化学院,湖北武汉 430081)

0 引言

齿轮箱是各种工程机械中的关键设备,一般用于传递扭矩或者改变转矩方向。由于负载大、转速高和润滑条件恶劣,导致齿轮箱经常出现点蚀、断齿和磨损等故障[1-2]。而随着故障的持续演化,齿轮箱振动信号中会出现大量的谐波分量,加剧振动噪声并造成严重的安全事故。因此,需要建立针对齿轮箱的故障诊断模型。

目前,齿轮箱的故障诊断模型一般基于振动信号进行开发[3]。随着各种特征提取指标的陆续提出,以样本熵、排列熵等非线性数据复杂度测量指标为代表的故障特征提取方法被广泛应用于齿轮箱的故障诊断[4-6]领域。例如,高素杰等人[7]将排列熵与局部均值分解相结合,用于提取齿轮箱的故障特征,诊断结果验证了该方法的有效性;然而排列熵只能开展信号的单一尺度分析且忽略了信号中的振幅信息。

针对信号的多尺度分析,研究人员进行了大量的研究。YUAN Xu-yi等人[8]基于粗粒化处理和加权排列熵,提出了多尺度加权排列熵,并将其用于提取高压隔膜泵的故障特征,诊断结果表明,该方法提取的故障特征实现了故障的精准识别目的;然而传统粗粒化处理会造成大量的有效信息被忽略,降低特征的质量。随后,DONG Zhi-lin等人[9]基于时移粗粒化处理,提出了时移多尺度加权排列熵算法,并用于滚动轴承的故障诊断,结果表明,时移粗粒化处理性能优于传统的粗粒化处理;然而无论是多尺度加权排列熵还是时移多尺度加权排列熵,均无法提取信号的高频故障特征。为此,KE Yun等人[10]构造了平均算子和差分算子,提出了层次加权排列熵,并用于提取共轨喷油器的故障特征,该方法准确表征了不同故障的特性;然而传统的层次分析由于层次处理较为粗糙,导致两种算子遗漏了大量有效信息。

为了提高传统层次处理的分析精度,LI Yong-bo等人[11]提出了一种改进层次排列熵算法,对层次处理进行了修正,提高了层次序列包含的信息量;然而改进的层次排列熵忽略了信号中的振幅信息,特征提取不足。ZHOU Fu-ming等人[12]提出了增强层次振幅感知排列熵算法,用于提取液压泵振动信号的故障特征,随机森林的诊断结果验证了该方法的有效性;然而,该算法对信号的长度要求较高,在样本长度较短时,分析精度较低,而当样本长度较长时,特征提取时间较长。为此,WANG Xian-zhi等人[13]提出了一种新的复杂性测量方法,称之为多尺度多样性熵(multiscale diversity entropy,MDE),相较于其他指标,MDE的效率非常高,且鲁棒性非常强;然而MDE的粗粒化处理存在不足。为此,YU Guang-wei等人[14]提出了复合多尺度多样性熵(composite multiscale diversity entropy,CMDE),并将其用于旋转机械的故障诊断,结果验证了该方法的有效性;然而CMDE无法提取信号的高频特征。随后,WANG Xian-zhi等人[15]1450-1451提出了层次多样性熵(hierarchical diversity entropy,HDE),将其用于轴承的故障诊断,结果表明,HDE性能要优于MDE;然而HDE的层次处理不够精细,造成特征提取得不够充分。

针对HDE特征提取不充分、不全面的缺陷,笔者借鉴增强层次分析的概念,对HDE进行改进,提出增强层次多样性熵;在此基础上,结合野马算法优化的支持向量机,提出一种基于EHDE和WHO-SVM的齿轮箱故障诊断方法。

首先,笔者利用EHDE提取齿轮箱振动信号的故障特征;随后,将故障特征输入至WHO-SVM分类器进行训练和测试;最后,根据分类器的输出完成样本的故障识别;利用齿轮箱实验数据,对EHDE方法在不同数据长度样本下的故障识别问题进行实验和研究。

1 增强层次多样性熵

1.1 多样性熵

对于序列X={x1,x2,…,xi,…,xN},X的多样性熵计算过程描述如下[16]：

1)基于给定的嵌入维数m,将时间序列X重构为一系列向量,如下所示:

(1)

2)构造相似集D(m),而D(m)可以通过计算相邻向量之间的余弦相似度来生成,具体如下所示:

(2)

(3)

4)多样性熵(diversity entropy,DE)可以定义如下:

(4)

对于时间序列X,当其DE值较大时,则代表X的复杂性较大;而当DE值较小时,证明其复杂性较小。因此,在[0,1]范围内,DE的熵值随着时间序列动态复杂度的增加而增加。

1.2 增强层次多样性熵值

多样性熵只是在单一尺度对时间序列进行了分析,而振动信号的状态信息分布在多个尺度上,这导致DE无法全面地描述信号的动态特性。为此,学者们陆续提出了MDE和HDE。

HDE避免了MDE只能分析信号低频特征的缺陷,但HDE的层次处理也不够精细,导致层次序列所包含的特性信息不够全面,进而导致特征质量不佳[17]。

为此,笔者对HDE进行了改进,提出了增强层次多样性熵,理论如下:

1)对于时间序列{X(i),i=1,2,…,N},定义时间序列的两个算子Q0和Q1如下:

(5)

(6)

式中:Q0为反映时间序列低频信息的算子;Q1为反映时间序列高频信息的算子。

(7)

3)定义向量{λ1,λ2,…,λk},则整数e可以表示为:

{λm,m=1,…,k}∈{0,1}

(8)

式中:λm为第m层的算子。

4)根据向量{λ1,λ2,…,λk},时间序列X的层次序列可以表示如下:

(9)

5)计算每个层次序列的多样性熵,则EHDE可以表示为:

EHDE(X,m,ε,k)=DE(Xk,e,m,ε)

(10)

在EHDE方法中,需要预先设置嵌入维数m、符号数ε、时间序列的长度N和层次分解的层数k这4个参数。

对于嵌入维数m,过小会导致重构向量Y(m)的长度过短,无法准确表征信号的动态特性;过大则造成重构向量的长度过长,造成DE无法提取信号中的细微变化,笔者将嵌入维数设置为m=4。

对于符号数ε,根据WANG Xian-zhi等人[15]1455的建议,笔者将其设置为ε=30。

对于时间序列的长度N,其取值对于算法性能的影响有限,但数据长度不能过短,否则会造成信号中包含的特征信息无法准确描述信号的动态特性,即分析得不够全面;其次数据长度不要过长,否则会严重降低信号分析的效率,同时分析精度也难以得到明显的提升[18]。

为获得较高计算效率的同时得到精确的计算结果,笔者将时间序列的长度设置为N=512。

对于层次分解的层数,一般设置为k≥3,该参数与特征的数量强相关,当k=3时,能够获得8个特征;而k=4时,能够获得16个特征。随着特征数量的增加,样本能够得到更加全面的表征,但同时会降低特征提取的效率。

综合考虑特征提取的效率以及特征表征的全面性,笔者将k设置为3。

1.3 仿真信号分析

1.3.1 参数分析

为了评估EHDE方法对数据长度的敏感性,笔者利用10组长度为128,256,512,1 024,2 048,4 096的高斯白噪声(white gaussian noise,WGN)和1/f噪声,对该算法进行分析。

不同长度噪声的EHDE分析结果如图1所示。

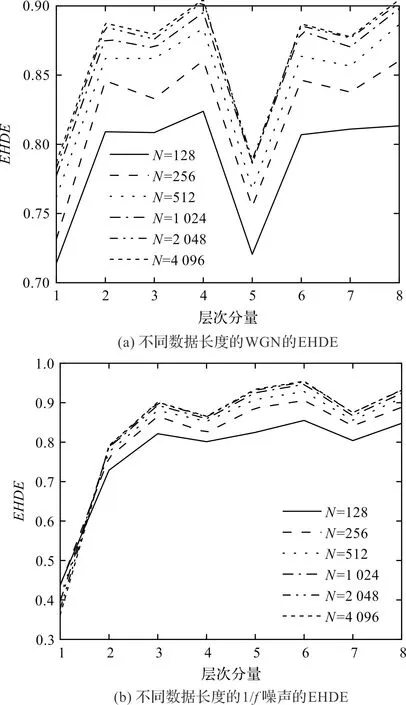
图1 不同数据长度的WGN和1/f噪声的EHDE

从图1可发现:在数据长度较小时(N≤256),两种噪声的EHDE熵值都出现了偏离,即复杂度测量得不够准确;而当数据长度N≥512时,两种噪声的熵值曲线基本重合,这证明在该数据长度下算法已经能够获得相对准确的复杂度测量结果。

此外,为了说明数据长度对计算效率的影响,笔者统计了不同数据长度下两种噪声的EHDE计算时间,如图2所示。

图2 不同数据长度下两种噪声的EHDE计算时间

由图2可知:随着数据长度的增加,EHDE的计算时间也随之增加,在数据长度N≤512时,计算时间没有显著增加;而当数据长度N=1 024时,此时算法的计算时间几乎是N=512时的两倍,但根据图1的结果,N=1 024和N=512获得的复杂度测量结果是基本一致的。

因此,从复杂度测量性能与计算效率两个方面考虑,笔者将长度设置为N=512是合理的。

1.3.2 性能对比分析

为了验证EHDE方法相对于其他方法的有效性,笔者利用被证明具有优异性能的精细复合多尺度样本熵(refined composite multiscale sample entropy,RCMSE)、精细复合多尺度模糊熵(refined composite multiscale fuzzy entropy,RCMFE)、精细复合多尺度排列熵(refined composite multiscale permutation entropy,RCMPE)、精细复合多尺度散布熵(refined composite multiscale dispersion,RCMDE)、精细复合多尺度波动散布熵(refined composite multiscale fluctuation dispersion entropy,RCMFDE)进行对比。其中尺度因子均设置为8。

每种方法的其他参数设置如表1所示。

表1 参数设置

随后,笔者利用10组长度为N=512的WGN和1/f噪声进行分析,利用EHDE和上述5种对比方法计算两种噪声的熵值,生成变异系数曲线,如图3所示。

图3 两种噪声的变异系数

由图3可知:随着分量的增加,6种方法的变异系数随之增加,这是因为随着层次分量和尺度因子的增加,层次序列和粗粒化序列的长度也显著减小,从而导致熵值测量的误差增大。

此外,RCMPE的变异系数最小,其次是EHDE,而变异系数反映了数据沿着平均值波动的幅度比例,数值越大意味着波动性越大,因此RCMPE的性能稳定性最好,而EHDE次之。

RCMSE的性能弱于RCMFE方法,而RCMFE是在RCMSE的基础上进行改进得到的,这说明变异系数能够评估算法的有效性。

2 野马算法优化支持向量机

2.1 野马优化算法

野马优化(WHO)算法是2021年提出的一种新的启发式优化算法,该算法主要通过模拟野马种群的各种生活行为来模拟寻优的过程[19-20]。

WHO的寻优过程包含三种行为,分别是放牧行为、交配行为、团队领导行为。在该算法中,野马个体的类型分为公马、母马和小马驹,公马职责在于领导种群中的其他个体。

在大多数时间里母马和小马驹处于放牧的过程中,其位置更新公式如下:

(11)

(12)

IDX=(P==0)

(13)

(14)

(15)

当小马驹长大后,会远离种群并开始交配行为,此时的位置更新方式为:

(16)

最后,领导者引领种群去往适宜的生存区域,对于已被占领的区域将进行争夺,若失败则会去往别的生存区域,领导者的位置更新方式为:

(17)

在种群的各种行为中,若出现了优于领导者适应度的个体,两者会互换身份,定义如下:

(18)

式中:cost为适应度函数;StallionGi为种群领导者的位置;XG,i为种群个体的位置。

2.2 野马算法优化支持向量机

支持向量机因为泛化性强,适用于小样本而被广泛用于模式识别领域。但广泛的研究表明,SVM中的惩罚系数C和核函数参数g对性能的影响非常大,如果设置不当可能会造成过拟合或欠拟合,进而影响模式识别的准确率[21]。

为此,笔者采用野马算法对SVM的参数进行优化,具体的优化步骤如下:

1)初始化野马算法的参数,分别是种群规模、最大迭代次数、领导者的比例和交配的概率等;

2)求解野马种群个体的适应度值,生成野马种群以及相应的领导者;

3)对野马种群的位置进行更新,同时对野马种群中领导者的位置进行更新;

4)更新野马种群的适应度值,若野马种群存在适应度值优于领导者适应度的个体,则按照式(18)替换领导者;

5)判断当前是否达到了最大的迭代次数,如果是则结束循环,否则跳转至步骤2);

6)输出领导者的坐标,即为SVM分类器的参数组合。

3 基于EHDE和WHO-SVM的流程

在上述内容中,EHDE被证明具有优异的信号复杂度测量性能,能够稳定和有效地分析非线性时间序列。为此,笔者将其用于齿轮箱故障振动信号故障特征的提取,结合野马算法优化的支持向量机,提出了一种基于EHDE和WHO-SVM的齿轮箱故障诊断方法。

齿轮箱故障诊断具体流程如下:

1)假定齿轮箱有着K类工况,每类工况的样本数量分别为M1,M2,…,MK,振动信号的长度为512;

2)计算每类每个样本振动信号的EHDE值,得到K个故障特征集;

3)将K个故障特征集的每个故障特征集分为MK/2个训练样本和MK/2个测试样本;

4)将训练样本输入到WHO-SVM中进行训练,建立参数最优的SVM分类器;

5)通过测试样本对WHO-SVM分类器进行测试,根据分类器的输出结果来判断齿轮箱的故障工况。

4 实验及结果分析

4.1 数据验证

实验数据采用QPZZ-II齿轮箱振动数据集。该实验平台由一个0.75 kW变转速的驱动电机、齿轮箱、配重盘、磁粉制动器和调速装置组成;通过调整配重、磁粉制动器的负载电流和调速装置的转速,来快速模拟齿轮箱的不同故障和不同工况。

该齿轮箱实验平台如图4所示。

图4 齿轮箱实验平台

图4中,齿轮箱包含1个模数为2,齿数为75的大齿轮以及1个模数为2,齿数为55的小齿轮,两个齿轮的材料均为S45C,采用油润滑,滚动轴承的型号为N205。电机的转速为880 r/min,负载电流为0.05 A,传感器的采样频率为5 120 Hz,传感器的布置位置为输出轴电机侧轴承的Y方向。

笔者利用电火花技术在齿轮上加工出不同的故障,收集了齿轮箱在正常、点蚀、断齿、磨损和点蚀磨损5种工况的振动信号,每种工况振动信号取100组样本,样本的点数为512。

5种信号的波形,如图5所示。

图5 齿轮箱振动信号的波形及频谱

首先,笔者计算齿轮箱振动信号的EHDE,结果如图6所示。

图6 齿轮箱振动信号的EHDE值

由图6可以发现:在不同的层次节点上,EHDE能够较好地区分齿轮箱样本,如在节点为1和2时,5种样本的EHDE熵值具有非常大的差异。此外,在节点为1时,正常样本的熵值小于故障样本的熵值,这是因为在齿轮箱未发生故障时,振动信号中的成分主要是环境噪声等成分已知的分量;而当齿轮箱发生故障后,振动信号中将出现各种频率及其倍频的成分,导致故障振动信号变得复杂,进而产生较大的熵值。

因此,可以证明EHDE可以较好地测量振动信号的复杂度,同时还可以区分正常和故障样本。

随后,为了进一步地识别齿轮箱的故障类型,笔者将故障特征输入至WHO-SVM模型中进行故障的识别;同时,为了验证EHDE方法的优越性,将由RCMSE、RCMFE、RCMPE、RCMDE和RCMFDE提取的故障特征输入至WHO-SVM中进行故障识别。

故障识别结果如图7所示。

图7 6种故障诊断方法的故障识别结果

由图7可以发现:EHDE-WHO-SVM方法在识别时,有3个样本被错误地识别为其他类型的样本,识别的准确率为98.8%,而其他故障诊断方法的准确率均低于该方法。这证明了EHDE方法的优越性,同时也证明其在数据长度较小时也能够获得准确的故障识别结果。

随后,为了进一步对比特征提取的效率,笔者统计了6种方法的特征提取时间以及相应的识别准确率,如表2所示。

表2 6种方法的故障识别结果

由表2可知:EHDE方法的准确率最高,RCMDE方法的准确率次之,而EHDE的特征提取时间仅少于RCMPE方法,为37.54 s。

综合来看,EHDE方法的准确率比RCMDE方法的准确率提高了4.8%,而特征提取时间多了23.56 s,但该时间成本能够接受。

其次,为了进一步评估EHDE等6种方法的诊断稳定性,笔者将特征输入至WHO-SVM中进行20次实验,统计每次实验的分类结果,如表3所示。

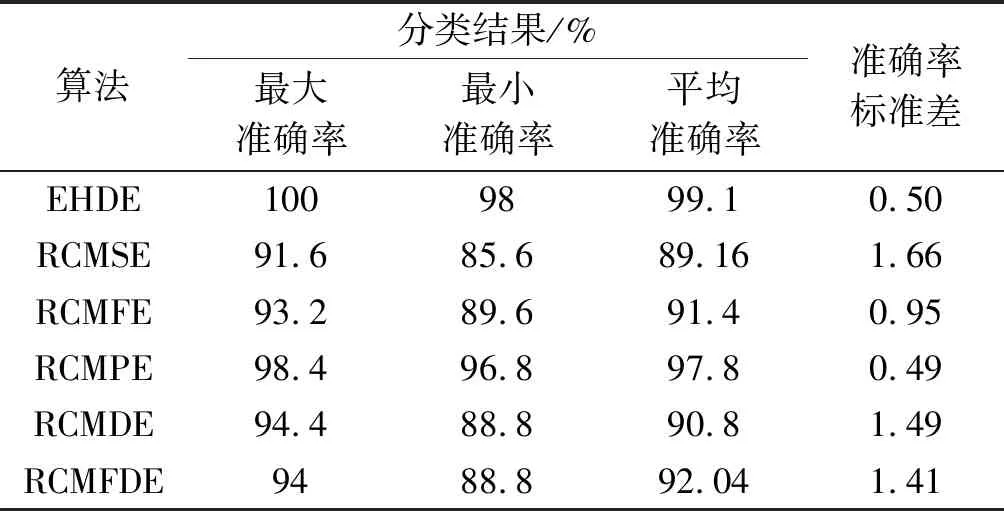
表3 多次实验下不同算法的故障识别结果

由表3可知:EHDE的最大准确率、最小准确率、平均准确率均优于其他5种对比方法,证明了EHDE方法具有优异的诊断性能,能够保证每次实验都可以准确地识别齿轮箱的故障类型。

RCMPE的诊断性能仅次于EHDE方法,但其特征提取时间远多于EHDE方法,因此EHDE的综合性能远优于RCMPE方法。

同样的,RCMSE方法的平均识别准确率最低,这证明了RCMSE在提取短时间序列的故障特征时存在较大缺陷,而RCMFE方法的准确率高于RCMSE,更加证明了此次分析的正确性。

为了验证数据长度对算法性能的影响,笔者对不同数据长度下6种方法的故障识别结果进行了分析,诊断准确率取20次实验的平均结果,如表4所示。

表4 不同数据长度下6种方法的诊断结果

从表4可以发现:在不同数据长度下,EHDE方法的准确率都高于其他5种方法,即使数据长度仅为128,EHDE方法的平均识别准确率也达到了80%以上;当数据长度为256时,EHDE方法的平均准确率已经能够达到90%以上,这证明了EHDE方法对数据长度的变化不敏感,即使数据长度较短,依然能够获得较为可靠的故障识别结果;当数据长度为1 024时,EHDE方法已经可以取得100%的识别结果,证明了EHDE方法的有效性。

此外,当数据长度为128时,RCMPE方法的准确率非常低,仅为66.16%;当数据长度为256时,平均识别准确率为76.4%;而当数据长度为512时,平均识别准确率已经高达97.8%,比前者提高了21.4%,这证明RCMPE方法对数据长度非常敏感。

最后,笔者对不同特征数量下的6种方法的识别准确率进行了对比分析,结果如图8所示。

图8 不同特征数量下6种方法的故障识别结果

由图8可以发现:随着用于分类的特征数量的增加:6种方法的故障识别准确率也随之显著增加,而EHDE方法在特征数量为4后,准确率曲线也在其他方法的上方,这证明EHDE方法仅需较少的特征即可以表征齿轮箱的故障特征;当输入的特征数量达到5个时,EHDE方法的准确率达到最大,此后准确率反而降低,这是因为部分特征存在冗余,特征之间互相干扰,进而影响了故障识别的准确率。

综上,EHDE方法在诊断稳定性、诊断精度和诊断效率方面都具有较强的性能,综合指标优于其他5种特征提取方法。

为了对EHDE方法的泛化性进行分析,笔者对齿轮箱的转速和负载电流进行了更换,当转速为880 r/min时,负载电流分别为0 A、0.05 A、0.1 A和0.2 A;当转速为1 470 r/min时,负载电流为0 A,上述5种工况依次称为工况1、工况2、工况3、工况4和工况5;同时,考虑了传感器的安装位置对故障识别结果的影响。

传感器的不同安装位置如表5所示。

表5 传感器的不同安装位置

笔者采用EHDE方法对不同工况下不同来源的振动信号进行分析,并进行故障特征提取和故障识别,结果如表6所示。

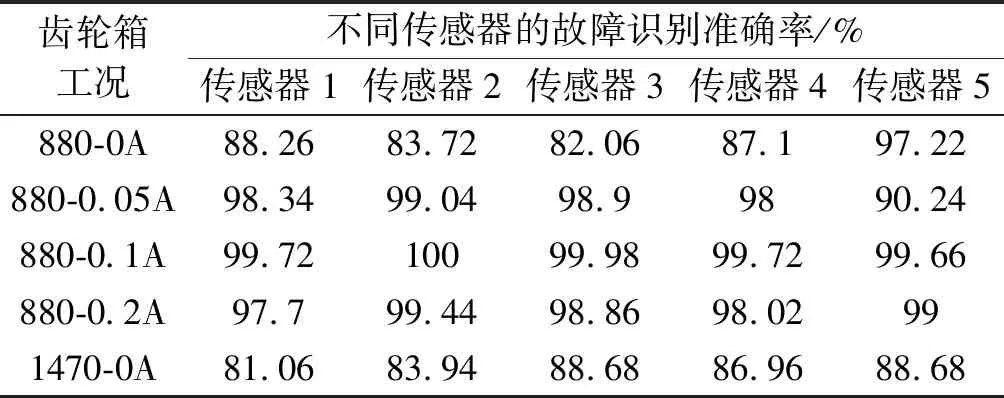
表6 齿轮箱不同工况下不同传感器的故障识别结果

从表6可以发现:传感器1的故障识别准确率比较低,而其他传感器的故障识别结果随着工况的变化而变化,无法具体评估有效性,但总的来说除传感器1外,其他传感器都可以获得较可靠的故障识别结果。此外,有负载工况的识别准确率要高于未受到负载的识别准确率,这是因为受到负载后,齿轮箱的振动信号会加剧,信号中的各种故障成分较多,因而故障属性得到了加强。

笔者使用由传感器2采集的振动信号进行了实验,根据故障识别结果可以发现,该传感器所取得的故障识别结果较为优异。

总之,EHDE方法可有效地识别不同工况和不同位置的齿轮箱故障。

4.2 泛化性分析

为了进一步验证EHDE和WHO-SVM故障诊断方法的泛化性,笔者利用东南大学提供的行星齿轮箱数据集进行实验,实验平台如图9所示。

图9 齿轮箱故障模拟实验装置

在该实验平台中,电机的转速为1 200 r/min和1 800 r/min两种,对应的负载分别为0 Nm和7.68 Nm,笔者选择1 800 r/min和7.68 Nm工况下的数据进行分析;通过布置在行星齿轮箱表面的加速度计以5 120 Hz的频率,采集正常、齿轮裂纹、齿轮磨损、齿根裂纹和齿面磨损5种状态下的振动信号。

每种工况振动信号取100组样本,样本的点数为2 048,5种信号的波形,如图10所示。