非对称部分斜拉桥线形控制影响因素对比分析

李 丹 肖永久 王常峰

（烟台大学，山东 烟台 264005）

0 引言

斜拉桥因其外形优美，构造轻柔且具有较大的跨越能力而倍受人们的喜爱。斜拉桥在大跨径桥梁中占据了极其重要的地位，成为现代桥梁技术发展的一个重要方向[1]。部分斜拉桥是近年来国内外新兴的一种介于连续梁和斜拉桥之间的过渡桥型，具有梁刚、塔矮、索倾角小、无索区段大等特点[2-3]。部分斜拉桥在施工过程中施工监控的最根本要求是要保证桥梁结构的安全性和可靠性，具体表现为确保施工过程中部分斜拉桥结构的内力和线形变化始终处于可控的安全范围内[4]。

王军玺[5]、张善等[6]都建立了以主梁线形控制为主斜拉索索力和主梁应力兼顾的监控系统；李忠三等[7]对荆岳长江公路大桥的结构参数进行敏感性分析，优化了计算模型，保证了大跨度混合斜拉桥的施工控制的精度；刘榕等[8]研究了影响温州瓯江特大桥结构内力、变形和自振特性等设计参数的变化情况并定量地了解各参数对于结构力学性能的影响程度；杨辉[9]介绍了四川涪江五桥主梁悬臂施工过程中线形控制的主要内容及其方法，详细讲解了斜拉桥大跨径线形控制的要点和关键工序；孙建渊等[10]结合漳州战备大桥的施工控制的特点，介绍了漳州战备大桥施工控制的基本原理以及实验方法。

本文以（35+168+136+35）m斜拉桥为工程实例，分析斜拉桥的线形控制影响因素，以促进斜拉桥施工控制技术在国内的推广和应用，也为类似斜拉桥的研究提供重要的参考价值。

1 工程概况

新建上海经苏州至湖州铁路跨常台高速苏嘉航线（35+168+136+35）m预应力混凝土非对称独塔部分斜拉桥，全长375.7m，其主跨168m跨越常台高速，边跨136m跨越苏嘉运河。箱梁最低点梁高在梁端及跨中4.5m，主跨辅助墩处6.5m，桥塔处8.5m。桥塔处墩、塔、梁固结，其他支墩处纵向活动。梁体采用外侧斜腹板单箱双室混凝土箱梁，顶宽14.3m，其控制断面宽度和梁高按圆曲线变化。斜拉索采用空间双索面体系，梁上间距6.0m，与主梁采用成品梁端锚具形式，主梁内设置锚固梁，张拉端设置在梁上，斜拉索采用单根张拉[11]。

该桥为非对称结构，施工工序复杂，小里程边跨采用满堂支架现浇施工、大里程边跨采用悬臂浇筑施工、主跨采用挂篮悬臂浇筑施工，大里程主跨的合拢段与小里程主跨的合拢段浇筑时间不一致，先合拢大里程侧再合拢小里程侧。主梁立面布置图如图1所示。

图1 主梁立面布置图

2 有限元模型

通过有限元软件Midas∕civil建立了非对称独塔部分斜拉桥的施工仿真模型，其中包括410个节点，52个受拉索单元，310个梁单元，130个施工阶段。有限元模型如图2所示。

图2 斜拉桥空间有限元模型

3 线形控制参数敏感性分析

该桥采用悬臂施工，施工过程中每个施工步骤如浇筑混凝土、张拉预应力、张拉斜拉索对结构的变形均有较大的影响。高速铁路对梁面的线形要求较高，因此施工过程中需要确定重要的影响因素，对其进行重点控制。

对于大跨度非对称部分斜拉桥，其线形控制的影响因素很多，为了解这些设计参数对斜拉桥线形监控的影响程度，本文选取材料弹性模量、材料容重、预应力管道摩擦系数、控制应力这四个主要因素进行探讨，选取斜拉桥施工的成桥阶段（二期恒载加载完成）作为研究对象，在原设计参数的基础上分别增大以及减小5%和10%，然后分析各参数对累计位移的影响[11]，对施工监控关键参数进行敏感性分析，以便为斜拉桥施工误差的修正提供科学依据。

3.1 混凝土容重对主梁线形控制的影响

斜拉桥有限元模型中主梁采用 C60 混凝土，混凝土容重的规范值为25kN∕m3。为分析混凝土容重对主梁线形控制的影响，以规范值为基准，分别取容重标准值按照偏差-10%，-5%，0%，5%，10%进行分析，得出主梁成桥十年阶段累计位移数据。混凝土容重的变化对主梁累计位移的影响见图3。该阶段不同混凝土容重偏差与混凝土容重规范值的位移差值见图4。

图3 混凝土容重对主梁累计位移的影响曲线图

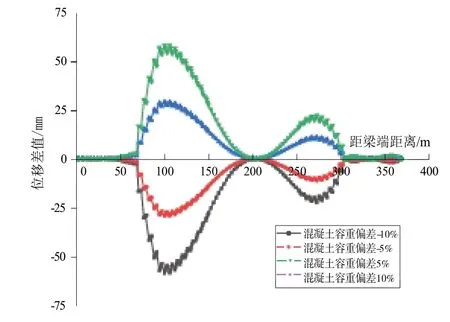
图4 混凝土容重的主梁位移差值曲线图

由图3可以看出，混凝土的容重发生变化时，主梁累计位移变化明显。随着混凝土容重的增加，主梁的累计位移也随之增加。

由图4可以看出，混凝土容重偏差与规范值的位移差值变化随混凝土容重的增大而增大，混凝土容重增大或减小5%和10%时，主梁挠度差分布大致对称，且具有类似变化趋势，混凝土容重减小10%时主梁挠度下挠变化的最大值减小了61.79mm，混凝土容重增大10%时主梁挠度上挠变化的最大值增加了61.42mm。

3.2 混凝土弹性模量对主梁线形控制的影响

材料弹性模量是影响桥梁结构强度最重要因素，并随时间的推移而变化，与结构变形有着直接关系。以规范值为基准，分别取弹性模量标准值按照偏差-10%，-5%，0%，5%，10%进行分析，得出主梁成桥十年阶段累计位移数据。主梁弹性模量的变化对主梁累计位移的影响见图5。该阶段不同混凝土弹性模量偏差与规范值的位移差值见图6所示。

图5 混凝土弹性模量对主梁累计位移的影响曲线图

图6 混凝土弹性模量的主梁位移差值曲线图

由图5可以看出，当混凝土的弹性模量降低时，主梁挠度随之增加。但混凝土弹性模量的变化对斜拉桥的影响效果并不显著。

由图6可以看出，混凝土弹性模量偏差与规范值的位移差值变化随混凝土弹性模量的增大而减 小，混凝土容重增大或减小5%和10%时，主梁挠度差分布基本对称，且具有类似的变化趋势，混凝土弹性模量减小10%时主梁挠度下挠变化的最大值减小了3.66mm，主梁挠度上挠变化的最大值增加了4.02mm。

3.3 摩阻系数与孔道偏差系数对主梁线形控制的影响

该桥的孔道摩阻系数μ=0.23，孔道偏差系数k=0.0025，为计算分析孔道摩阻系数和孔道偏差系数的改变对主梁线形控制的影响，分别取μ=0.20、k=0.0020；μ=0.23、k=0.0025；μ=0.26、k=0.0030；μ=0.29、k=0.0035四种工况进行分析，得出主梁成桥十年阶段累计位移数据。主梁孔道摩阻系数和孔道偏差系数的改变对主梁累计位移的影响见图7所示。

图7 混凝土摩阻系数与孔道偏差系数对主梁累计位移的影响曲线图

由图7可以看出，混凝土摩阻系数与孔道偏差系数取值不同时，主梁的累计位移变化很小，混凝土摩阻系数与孔道偏差系数的变化对斜拉桥主梁线形的影响几乎可以忽略，可以不做考虑。

3.4 张拉控制应力对主梁线形控制的影响

斜拉桥预应力钢束采用公称直径为15.20mm的高强度钢绞线，该斜拉桥主梁钢绞线有17-Φs15.2 和22-Φs15.2两种类型，纵向预应力体系的锚下张拉控制应力为1302MPa，张拉方式采用两端张拉。

为分析张拉控制应力对主梁线形控制的影响，以预应力设计值为基准，分别计算超张拉5%、10%以及欠张拉5%、10%时，主梁成桥十年阶段预应力对主梁累计位移的影响。其张拉控制应力变化对主梁累计位移的影响见图8所示。

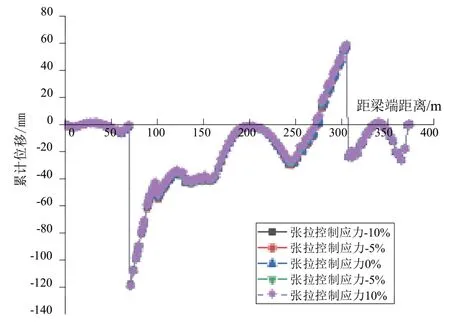
图8 混凝土张拉控制应力对主梁累计位移的影响曲线图

由图8可以看出，混凝土张拉控制应力取值不同时，主梁的累计位移变化很小，张拉控制应力的变化对斜拉桥主梁线形的影响几乎可以忽略，可以不做考虑。

4 结束语

通过对该斜拉桥的主梁施工线形控制影响因素分析，经分析四种参数变化的情况可发现，混凝土容重对主梁线形影响显著，其余参数相对影响较小。

采用悬臂施工的非对称部分斜拉桥，容重对结构变形影响较大，需要考虑梁内普通钢筋对结构容重的影响。在容重偏差约5%的情况下（体积配筋率大约为 0.29%），影响已达到129.5mm，已超出规范限值，所以需要重点分析，在施工中需要重点控制。因此，在桥梁的浇筑施工过程中必须严格按照规定控制混凝土的容重，以确保桥梁的设计挠度。