具有保凸性的三点二重逼近细分格式
2024-04-22李志明
王 燕,李志明
(1.合肥师范学院 数学与统计学院,安徽 合肥 230601;2.合肥工业大学 计算机与信息学院,安徽 合肥 230009)
0 引言
细分曲线曲面作为一种重要的曲线曲面造型的方法,因其简单、易操作,一直是学者研究的重点[1-17]。比较经典细分格式的有Dyn[2]提出的四点二重插值细分格式,Weissman[3]提出的六点二重插值细分格式,Hassan等[4-5]提出的三重插值细分格式,包括三点三重和四点三重两类,Chaikin[6]提出的割角细分格式。后来的学者在这些经典细分格式的基础上,又提出了很多新的细分格式,并且研究了这些细分格式的性质,比如Siddiqi[7]提出了一类具有C2连续性的三点二重细分格式;黄树培等[8]提出了一类三点二重插值细分格式,并研究了其保凸性、分形的性质。在上述研究的基础上,本研究提出了一种三点二重逼近细分格式,这种格式是非对称的,证明了它具有C1连续性,并给出了它具有保凸性的参数取值范围,最后通过实例证明了这种格式的有效性。
1 预备知识
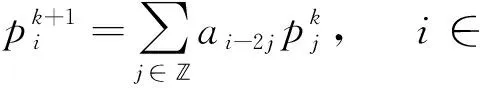
(1)
为二重细分格式,其中a={ai}i∈是相对应的细分格式的Mask(掩模)。
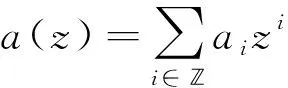
定理1[9]若二重细分格式S一致收敛,则其Maska={ai}i∈必须满足
(2)
定理2[9]若二重细分格式S的掩模a={ai}i∈满足(2)式,则必存在一个二重细分格dPk=S1dPk-1成立,其中一般地,将Sn记为S的n阶差分格式,为其掩膜,则为Sn的生成多项式。
定理3[9]若二重细分格式S的掩模a={ai}i∈及其j阶差分格式Sj(j=1,2,…,n)的掩模满足
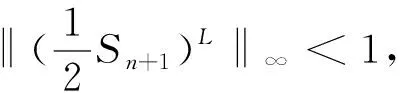
2 三点二重细分格式
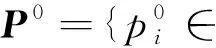
(3)
当μ=0时,格式(3)变为三次B样条细分格式:
定理4对于任意给定的初始控制多边形,当参数-3/16 <μ<5/16 时,由式(3)得到的极限曲线具有一致收敛性。
证明细分格式(3)的生成多项式为
a(z)=(1/8 +μ)z-2+(1/2 +μ)z-1+(3/4 -2μ)+(1/2 -2μ)z+(1/8 +μ)z2+μz3,
由定理2可得S1的生成多项式为
a(1)(z)=2za(z)/(1+z)=(1/4+2μ)z-1+3/4+(3/4-4μ)z+1/4z2+2μz3,
则
当-3/16<μ<5/16时,
‖1/2S1‖∞=1/2 max{|1/4 +2μ|+|3/4 -4μ|+|2μ|,3/4 + 1/4}<1,
由定理3可知,细分格式(3)生成的极限曲线是一致收敛的。
定理5对于任意给定的初始控制多边形,当参数-1/8 <μ< 1/4时,由式(3)得到的极限曲线的连续性是C1连续。当参数μ=0时,格式(3)得到的极限曲线具有C2连续性。
证明由定理2可得S2的生成多项式为
a(2)(z)=2za(1)(z)/(1+z)=(1/2+4μ)+(1-4μ)z+(1/2-4μ)z2+4μz3,
则
当-1/8 <μ< 1/4时,
‖1/2S2‖∞=1/2max{|1/2+4μ|+|1/2-4μ|,|1-4μ|+|4μ|}<1。
根据定理3,细分格式(3)得到的极限曲线具有C1连续性。
当μ=0时,
a(3)(z)=z+z2,‖1/2S3‖∞= 1/2 max{1,1}<1,
根据定理3,由细分格式(3)得到的极限曲线具有C2连续性。显然,细分格式(3)变为三次B样条细分格式。
3 保凸性
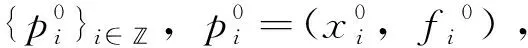
证明由细分格式(3)得
(4)
(5)
假设对某些k≥0,k∈,i∈成立,则当0≤μ≤1/8时,根据式(4)和式且则,i∈成立。定理6证毕。
因此当参数0≤μ≤1/8时,在给定的初始凸顶点下,由细分格式(3)得到了具有C1连续性的保凸曲线。
4 数值分析
文献[7]中给出的细分格式的系数是固定的、对称的细分格式,文献[8]中给出了一类插值型的三点二重细分格式,连续性最高达到C1连续。本文提出的三点二重细分格式是非对称的,并且带形状参数,具有可调节性,连续性最高是C2连续,与已有的三点二重细分格式的比较结果列于表1。
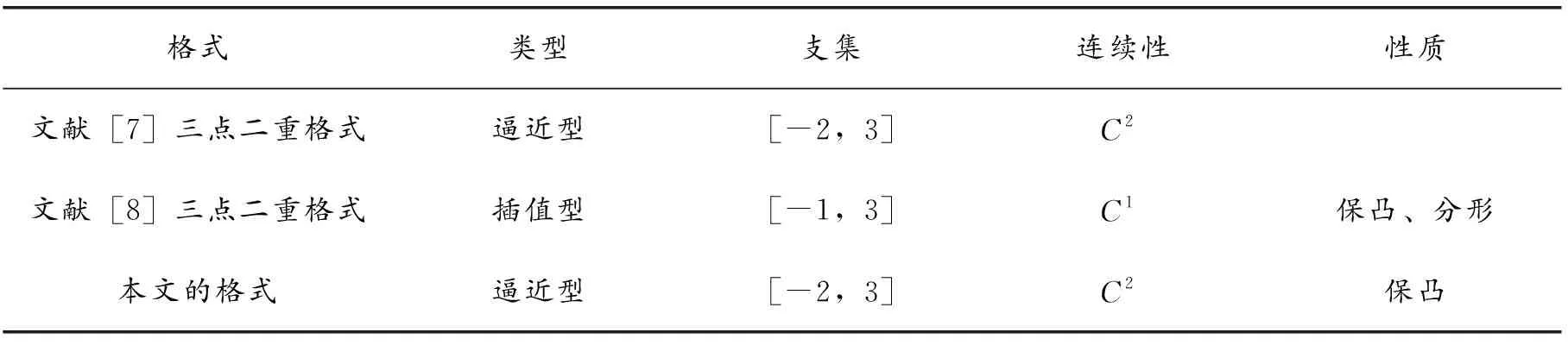
表1 与已有三点二重格式的比较
对于相同的控制多边形,当参数μ取不同值时,可以得到不同的造型曲线,见图1和图2。由图1、2可见,参数μ的引入增加了造型的灵活性。
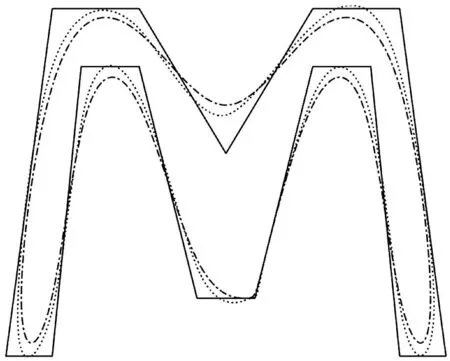
图1 由格式(3)生成的极限曲线(虚线为μ=-1/32,点划线为μ=0)
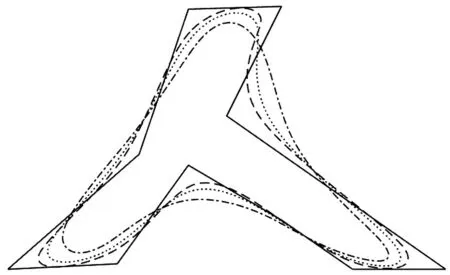
图2 由格式(3)生成的极限曲线(双划线为μ=-1/32,虚线为μ=0,点划线为
当参数0≤μ≤1/8时,由格式(3)可以生成具有保凸性的极限曲线,见图3,若初始给定的控制顶点是凸的,则由格式(3)生成的极限曲线也是凸的。

图3 由格式(3)生成的保凸曲线(μ=1/10)
5 结论
本文研究了一类新的三点二重逼近细分格式,给出了其不同的连续性对应的参数区间,这种格式的支集是[-2,3],是非对称的,且带形状参数,具有可调节性,连续性最高是C2连续,当参数在[0,1/8]取值时,生成的极限曲线具有保凸性,可以较好的用于工业设计。下一步,我们将继续研究该格式的其他性质,并尝试推广到曲面细分格式。
