光储直流微电网多运行工况稳定性分析

2024-04-22陈景文王福强王同新

智慧电力 2024年4期

陈景文，王媛，王福强，王同新，何舟

（1.陕西科技大学电气与控制工程学院，陕西西安 710021；2.立讯精密科技（西安）有限公司，陕西西安 710021）

0 引言

直流微电网中光伏发电单元、储能单元以及负载均是通过变换器连接在直流母线上。当各变换器之间阻抗不匹配时，即使其单独工作稳定，也可能会导致系统整体振荡失稳[1-3]。为保证系统处于稳定运行状态，对于系统整体稳定性的研究显得至关重要。

针对系统稳定性的分析主要有大信号分析法[4]和小信号分析法。小信号分析法研究系统在稳态点附近出现微小扰动时母线电压的波动情况[5]，其可利用系统状态空间方程[6-8]、传递函数[9-10]、阻抗进行稳定性分析[11-13]。与前2 种方法相比，基于阻抗的稳定性分析优势在于不需要获取变换器的详细信息，只需考虑接口特性，在复杂系统稳定性分析中，利用阻抗测量技术即可得到端口阻抗，因此该方法应用较为广泛。通过建立基于阻抗的系统小信号模型，利用稳定性判据对系统稳定性做出判断是稳定性分析的主体思路。对于系统稳定性判据的研究，首先由Middlebrook 提出1 种保守性较强的阻抗比判据，随后针对其保守性许多学者对该判据做出了改进[14]。然而上述判据均受系统功率流向限制，当系统中存在源、荷角色转变的单元时，无法对其做出明确区分[15]。对此，文献[16]提出1 种基于全局导纳的广义Nyquist 稳定性判据用以判断系统稳定性，并与现有阻抗判据作对比，分析两者的优缺点。文献[17]提出1 种基于Nyquist 判据的稳定性估计方法，以此估计系统允许接入恒功率负载的最大数量。文献[18]针对含有右半平面极点的系统提出1 种基于单一阻抗的稳定性分析方法。该方法考虑了开环传递函数包含右半平面极点的情况。文献[19]利用阻抗比判据对双母线直流微电网的稳定性进行判断，以此找到稳定裕度最小的运行状态。文献[16-18]只对直流微电网典型的1 种工况进行稳定性分析，很少考虑系统中各变换器的多种控制方式以及不同的运行模式。当考虑系统从1 种工况转变为另1 种工况，如储能单元由放电转为充电时，上述阻抗稳定判据的环路增益将发生改变，说明其对于多工况运行的系统通用性不强，这会对分析此类系统的稳定性带来不便。

针对上述问题，本文首先对光储直流微电网系统各变换器建立小信号模型，从而得到各变换器以及系统整体的阻抗模型。其次，利用光储直流微电网稳态工作点的存在条件及劳斯判据推导得出稳定时负载功率及母线电容的约束条件。之后，为得到通用性较强的稳定性判据，不再以系统内各单元的“源”、“荷”角色来定义环路增益，而根据系统内各单元对直流母线的控制量定义新的环路增益，即母线电压控制变换器（Bus Voltage Controlled Conoerter，BVCC）或是母线电流控制变换器（Bus Current Controlled Converter，BCCC），进而对系统进行稳定性分析，研究讨论不同工况、负载功率变化以及母线电容变化时，对系统稳定性的影响。最后，仿真验证理论分析结论的正确性。

1 光储直流微电网系统阻抗模型建立

1.1 光储直流微电网结构

光储直流微电网的结构如图1 所示，光伏、储能单元均与直流母线相连，同时，直流母线上经过DC-AC 变换器实现功率双向传输，负载包括电阻性直流负载，以及经DC-DC 变换器连接的恒功率负载，为简化分析，将系统传输线路阻抗统一等效到各变换器与直流母线连接处。本文着重对图1 中红色虚线框内的级联系统的稳定性进行分析研究。

图1 光储直流微电网结构图Fig.1 Structure of optical storage DC microgrid

1.2 光伏变换器阻抗模型

光储直流微电网中光伏变换器选用Boost 变换器，控制方式可采用基于增量电导法（Incremental Conductance Technique，INC）的最大功率点跟踪（Maximum Power Point Tracking，MPPT）控制或恒压下垂控制，2 种控制方式的小信号控制框图如图2 所示。

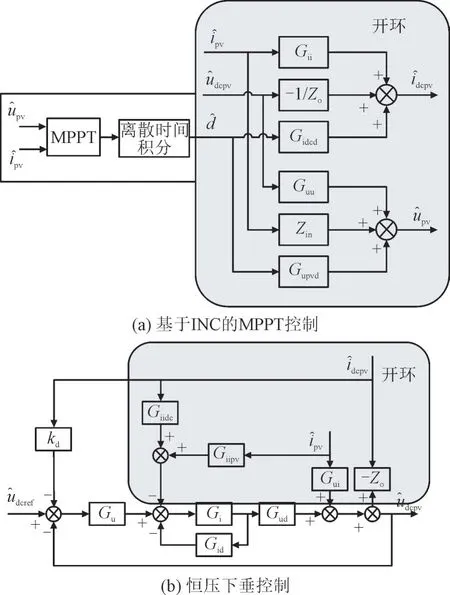
图2 Boost变换器小信号控制框图Fig.2 Block diagram of Boost converter with small signal control

图2（a）中，upv为光伏电池输出电压，也即光伏变换器输入电压；udcpv为光伏变换器输出电压；idcpv为光伏变换器输出电流；ipv为光伏变换器输入电流；“ˆ”代表小信号扰动量；Zo为输出电压到输出电流的开环传递函数；Guu为udcpv到upv的传递函数；Gidcd为d到idcpv的传递函数；图2（b）中，udcref为光伏变换器给定输出电压；Gu和Gi分别为电压、电流PI 调节器的传递函数；kd为下垂系数；Giidc为变换器idcpv到电感电流的传递函数；Gud为d到udcpv的传递函数；Gid为d到电感电流的传递函数。

由控制框图可以得出INC 控制下及恒压下垂控制下Boost 变换器的闭环输出阻抗ZpvM，ZpvC分别为式（1）、（2）所示：

1.3 储能变换器阻抗模型

储能变换器为Buck-Boost 变换器，其控制方式采用恒压下垂控制或恒流控制。Buck-Boost 变换器恒压下垂控制与Boost 变换器控制框图类似，由此得出变换器工作在Boost 模式与Buck 模式的闭环输出阻抗为：

式中：ZbcBoost和ZbcBuck分别为Boost 和Buck 工作模式下变换器输出阻抗；ZoBoost和ZoBuck分别为Boost和Buck 模式下变换器开环输出阻抗；下标“1”和“2”分别代表Boost 和Buck 工作模式下变换器相应传递函数.

恒流控制下Buck-Boost 变换器小信号控制框图如图3 所示。

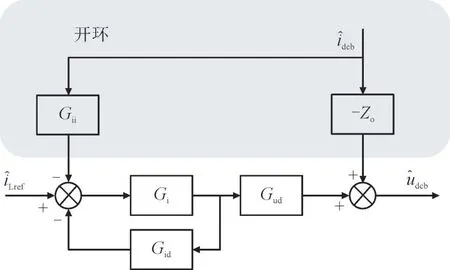
图3 Buck-Boost变换器恒流小信号控制框图Fig.3 Block diagram of Buck-Boost converter with constant current control

图3 中，udcb为储能变换器输出电压；iLref为储能变换器恒流控制的给定电流值；idcb为储能变换器输出电流。由控制框图可以得出恒流控制下Buck-Boost 变换器的闭环输出阻抗Zbi为：

1.4 负载变换器阻抗模型

负载变换器为Buck 变换器，采用恒压控制稳定输出电压，其小信号控制框图如图4 所示。

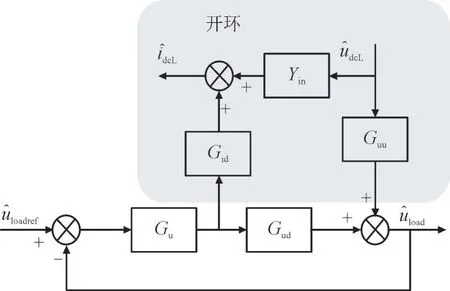
图4 Buck变换器恒压小信号控制框图Fig.4 Block diagram of Buck converter with constant voltage control

图4 中，Yin为输入电压到输入电流的传递函数；uload为负载变换器输出电压；uloadref为负载变换器给定输出电压；udcL为负载变换器输入电压。由控制框图得到恒压控制下Buck 变换器的闭环输入阻抗Zload为：

2 基于BVCC和BCCC的稳定性判据

在对级联系统的稳定性分析过程中，通常采用阻抗分析法。Middlebrook 判据最先被应用于输入滤波器与变换器构成的级联系统中[14]，后来逐步推广到源、荷级联系统。

源、荷级联系统整体输入输出关系式为：

式中：Zo_S和Zin_L分别为源子系统输出阻抗和负载子系统输入阻抗；vo_L为负荷子系统输出电压；vin_S为源子系统输入电压；vo_S为源子系统输出电压；vin_L为负荷子系统输入电压。

系统整体的环路增益Tm被定义为Tm=Zo_S/Zin_L，在各子系统均稳定的前提下，Tm满足Nyquist 稳定性条件即可保证源、荷级联系统整体的稳定。

对环路增益的定义存在一定的局限性。当系统中功率流反向时，如储能单元由放电模式转换为充电模式，此时源、荷子系统角色对调，所对应的环路增益与原来的环路增益相反。在分析多运行工况系统时需要根据工作情况进行讨论，使稳定性分析更显繁琐、通用性较弱。为解决此类问题，重新对级联系统中变换器的类型进行划分，根据变换器是控制直流母线电压或直流母线电流将其分为BVCC 或是BCCC[20]。基于BVCC 和BCCC 的级联系统等效模型如图5 所示。

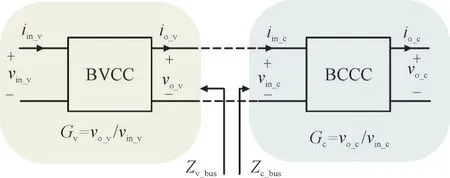
图5 BVCC、BCCC级联系统模型Fig.5 BVCC and BCCC cascade system model

图5 中，Gv和Gc分别为BVCC 子系统和BCCC子系统输入输出传递函数；Zv_bus和Zc_bus分别为BVCC子系统的输出阻抗和BCCC 子系统的输入阻抗。

系统整体的环路增益Tm被重新定义为Tm=Zv_bus/Zc_bus。由此定义的环路增益将不受功率流向限制，使储能恒压充电与恒压放电对应的环路增益表达式不发生改变，增强了判据的通用性。

3 光储直流微电网稳定性分析

3.1 稳定边界条件

光储直流微电网的统一等效电路如图6 所示，将采用恒压下垂控制的单元等效成电压源与电阻（下垂系数）的串联形式，将工作在最大功率控制下的单元及恒功率负载单元等效成一个电流源[21-22]。

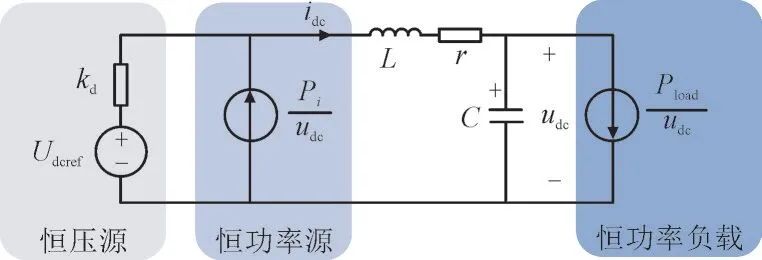
图6 光储直流微电网统一等效电路模型Fig.6 Unified equivalent circuit model of optical storage DC microgrid

图6 中，Udcref为恒压下垂控制下的光伏单元或储能单元的电压参考值；Pi（i=pv，b）为MPPT 控制的光伏单元或恒流控制的储能单元的功率，相当于恒功率源的功率；Pload为负载功率；L为线路电感；r为线路电阻；C为滤波电容。

由图6 知光储直流微电网等效电路数学模型为：

式中：udc为母线电压；idc为母线电流。

式中：Idc，Udc分别为稳态工作点电流和电压。由式（9）得到系统处于稳态时负载功率的约束条件为：

由式（8）得系统的状态方程的系数矩阵为：

令|sI-A|=0，得到系统的特征方程为：

由劳斯判据知系统稳定时满足：

稳态值Udc取值结合式（10），则得到：

式（14）即为系统稳定时负载功率Pload及母线电容C的边界约束条件。由式（14）得到系统在不同工况下维持稳定所需的负载功率值和母线电容值。

3.2 3种运行工况下光储直流微电网稳定性分析

光储直流微电网系统由3 种变换器以及线路阻抗、母线电容组成，其构成的阻抗传递函数为：

各变换器可以由其阻抗模型代替，微电网阻抗模型如图7 所示。工况1 光伏输出功率小于负载功率情况下，光伏采用MPPT 控制为负载提供最大功率，同时蓄电池补充不足功率；工况2 光伏输出功率略大于负载功率情况下，光伏仍采用MPPT 控制，多余的功率被蓄电池吸收；工况3 光伏输出功率远大于负载功率，光伏以恒压下垂方式向负载输送功率，蓄电池以恒流控制方式吸收剩余功率。

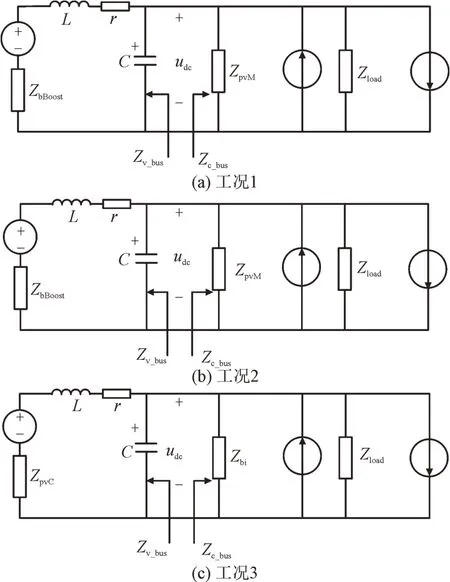
图7 3种工况下微电网阻抗模型Fig.7 Impedance model of microgrid under three operating conditions

3 种工况下光储直流微电网各变换器控制方式及系统等效环路增益表达式如表1 所示。

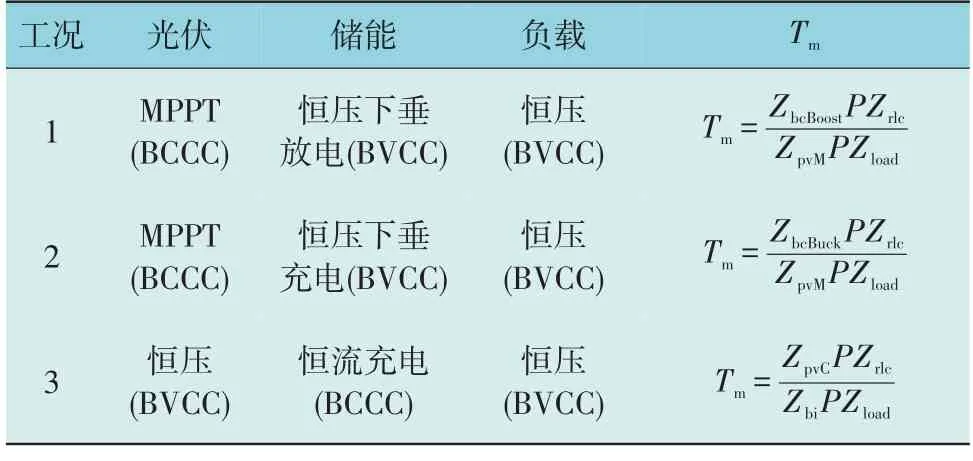
表1 各工况变换器控制方式及等效环路增益Table 1 Control mode and equivalent loop gain of converter under each working condition

分别对光储直流微电网3 种运行工况的Tm的Nyquist 曲线进行绘制，如图8 所示。

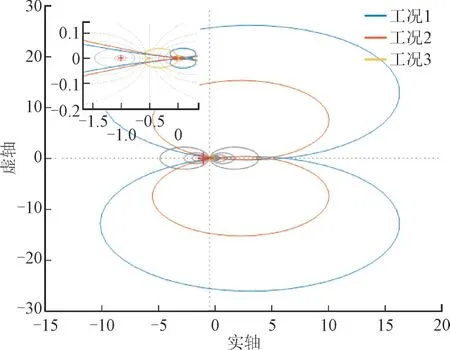
图8 3种工况下Tm的Nyquist曲线Fig.8 Nyquist curve of Tm under three operating conditions

由图8 可知，工况1 和工况2 对应的Tm的Nyquist 曲线相较于工况3 曲线更接近（-1，j0）点，即工况1 和工况2 稳定裕度较小，稳定程度低，而工况3 稳定程度较高。由此可见，当光伏变换器采用基于INC 的MPPT 控制，储能变换器采用恒压下垂控制时系统稳定性相对较差，需要选取合适的系统参数，确保运行在该工况下的微电网能够维持稳定。

3.3 系统参数对光储直流微电网稳定性的影响

3.3.1 控制器参数的选取

以储能变换器的电压控制器参数选取为例，讨论其比例系数kp和积分系数ki变化对稳定性的影响。当ki=20，kp分别取1，5，7 时系统Tm的Nyquist曲线如图9（a）所示；当kp=1，ki分别取20，30，60 时系统Tm的Nyquist 曲线如图9（b）所示。由图9 可以看出随着kp及ki的增大，系统Tm的Nyquist 曲线逐渐接近（-1，j0）点，稳定裕度降低，因此合适的控制器参数选为kp=1，ki=20。电流控制器参数的稳定性分析及选取与之类似，在此不再详细赘述。各控制器参数选取结果如表2 所示。

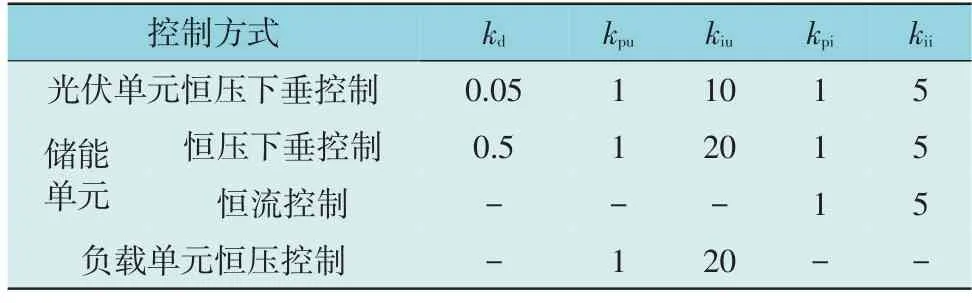
表2 仿真模型主要控制参数Table 2 Main control parameters of simulation model

图9 控制器参数变化时Tm 的Nyquist曲线图Fig.9 Nyquist curve of Tm with varying controller parameters

3.3.2 负载功率及类型对稳定性的影响

在系统控制器参数设计合理前提下，以运行工况1 下的光储直流微电网为例，分析负载功率大小及类型对微电网稳定性的影响。首先令恒功率负载的功率分别取15 kW，20 kW，50 kW，80 kW，绘制Tm的Nyquist 曲线如图10 所示。由图10 可以看出，负载功率增大，Tm的Nyquist 曲线将逐渐靠近负实轴，相位裕度逐渐减小。当功率达到50 kW 时图10 中红色曲线包围（-1，j0）点，稳定性不足。负载功率为80 kW 时曲线为图10中蓝色曲线，同样包围（-1，j0）点，系统不稳。

图10 负载功率变化时Tm 的Nyquist曲线图Fig.10 Nyquist curve of Tm with varying load power

为研究负载类型对系统稳定性的影响，绘制系统带电阻性负载与恒功率负载的Tm的Nyquist 曲线如图11 所示。由图11 可知，在输出功率同为50 kW的情况下，恒功率负载的Tm的Nyquist 曲线包围（-1，j0）点，而电阻性负载不包围（-1，j0）点，由此可见同等功率条件下电阻性负载与恒功率负载相比稳定裕度大，稳定程度高。本文设定母线电压值为600 V，光伏电池最大输出功率为12 kW，由式（14）得到稳定时负载功率应小于53 kW，在误差允许范围内，与图11 中50 kW 负载功率对应的Tm的Nyquist 曲线呈现结果基本一致。

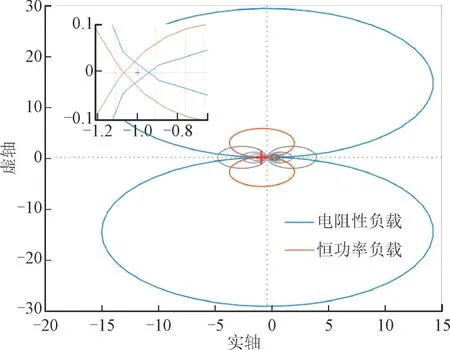
图11 不同类型负载对应Tm 的Nyquist曲线图Fig.11 Nyquist curve of Tm corresponding to different types of loads

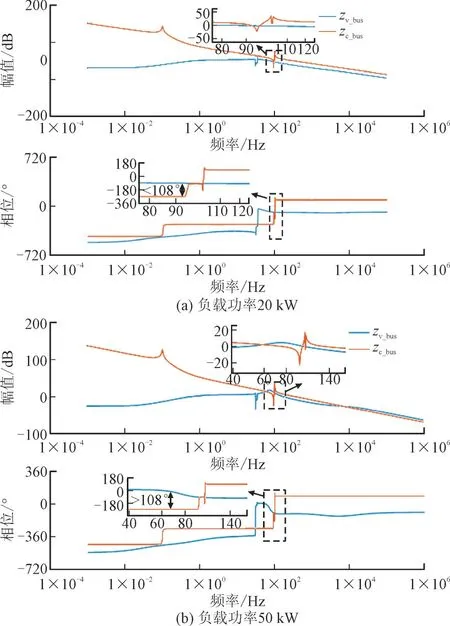
图12 直流微电网系统阻抗Bode图Fig.12 Bode diagram of DC microgrid system impedance

由图12（b）可知，在阻抗不匹配频段Zv_bus和Zc_bus的阻抗特性分别呈容性（相位90°）和感性（相位-90°），从物理角度揭示振荡的本质即系统中容抗与感抗在该频段正好相消，能量在等效电感与等效电容之间不断转移，而系统负阻尼特性将此能量放大，从而产生振荡失稳现象。从系统传递函数模型来看，将处于振荡频率附近的端口阻抗Zv_bus和Zc_bus分别用等效电容Cv_bus和等效电感Lc_bus表示如下：

式中：Rv_bus和Rc_bus分别对应各阻抗内的阻性部分。

系统闭环特征方程为：

将式（18）代入式（16）和式（17）得：

绘制系统整体的极点分布图如图13 所示。由图13 可知图中一对共轭极点是导致系统振荡的原因，系统在此对极点所在频率附近的容抗与感抗相消，内部形成振荡，而该对极点靠近虚轴，阻尼系数较小，对振荡抑制能力弱，使系统最终振荡失稳。

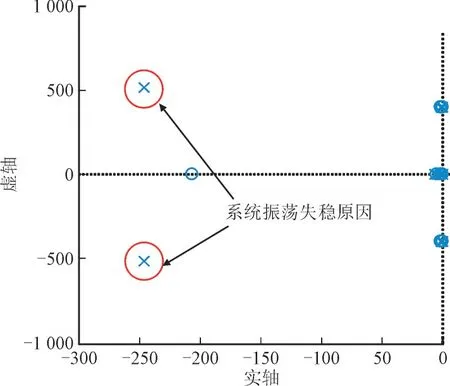
图13 系统极点分布图Fig.13 Pole distribution diagram of the system

3.3.3 母线电容对稳定性的影响

以运行工况1 下的光储直流微电网为例，研究母线电容大小对微电网稳定性的影响。令母线电容的容值分别取1 500 μF，2 500 μF，3 000 μF，5 000 μF，系统对应Tm的Nyquist 曲线图如图14 所示。随着母线电容的增大，Tm的Nyquist 曲线将逐渐远离（-1，j0）点，系统的相位裕度逐渐增大。同时，Tm的Nyquist 曲线逐渐缩小，即系统谐振峰值逐渐减小，使得系统稳定程度逐步提高。同样根据公式（14）可以得出合适的母线电容值应大于2 000 μF。图14 中蓝色曲线为1 000 μF 的母线电容对应的Tm的Nyquist 曲线，该曲线包围（-1，j0）点，表明系统不稳定，在误差允许范围内与计算结果基本一致。在实际母线电容的选取中，考虑到装置整体体积，因此电容选取为3 000 μF。

图14 母线电容变化时Tm 的Nyquist曲线图Fig.14 Nyquist curve of Tm with varying bus capacitance

4 仿真验证

为了对稳定性分析结论的正确性进行验证，在MATLAB/Simulink 环境中搭建图1 中红色虚线框内的仿真电路。设定母线电压600 V，负载输出电压200 V，各单元参数和控制器参数如表2 和表3 所示。各变换器端口电压及功率见表4。

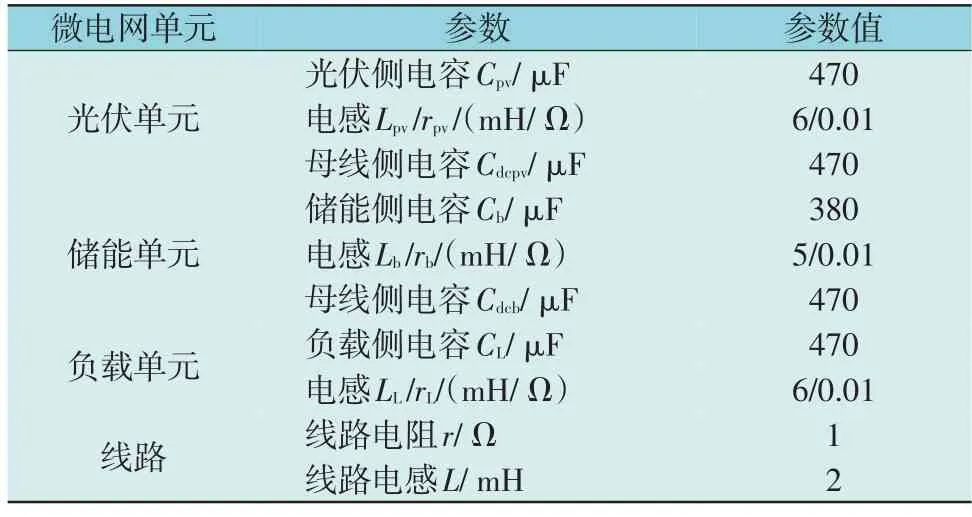
表3 仿真模型主要电路参数Table 3 Main circuit parameters of simulation model

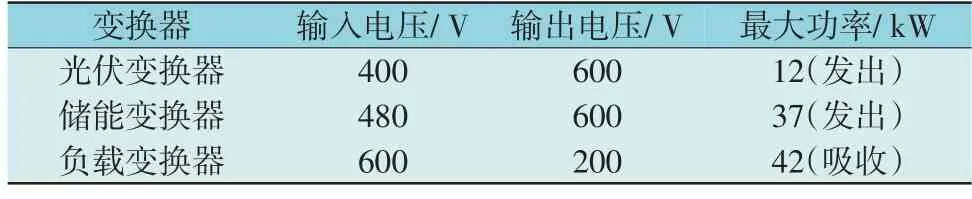
表4 各变换器输入输出电压及功率Table 4 Input and output of voltage and power of each converter

针对本文所述微电网3 种运行工况的稳定性进行验证，3 种工况下的母线电压波形如图15 所示。

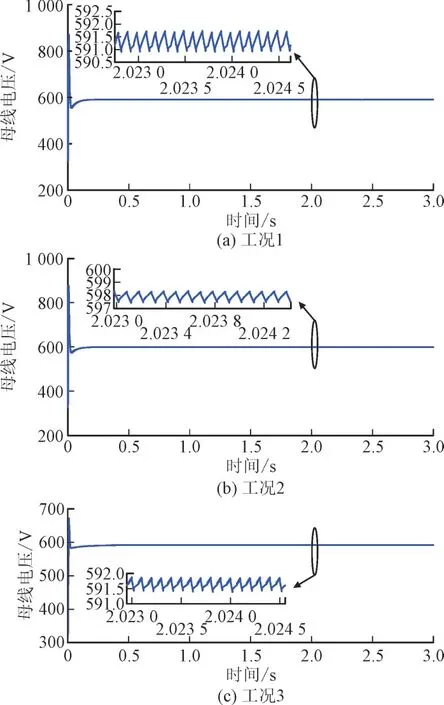
图15 3种工况下直流微电网母线电压波形Fig.15 Bus voltage waveform of DC microgrid under three working conditions

图15 中3 种工况母线电压均处于稳定状态，但电压波动大小不同，工况1 与工况2 母线电压波动范围较大，稳定裕度较低，工况3 稳定裕度较高，仿真分析结果与理论分析基本一致。

为验证母线电容对系统稳定性的影响，设定母线电容为1 500 μF 和3 000 μF，仿真得出母线电压波形分别如图16（a），（b）所示。

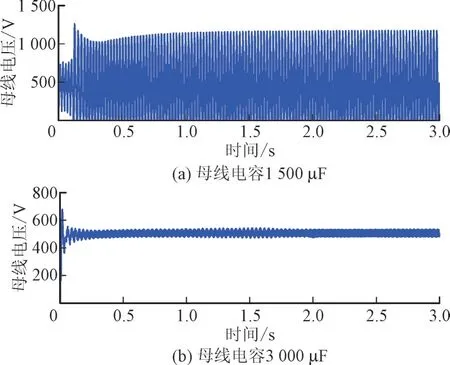
图16 不同母线电容对应母线电压波形Fig.16 Bus voltage waveform correspond to different bus capacitance

由图16 可知，在母线电容值较小时，系统阻抗不匹配导致母线电压出现较大幅度的振荡现象；当母线电容值大于系统稳定所需母线电容值时，系统谐振峰值较小，使得母线电压波动程度逐渐减小，与前文分析结果吻合，由此验证母线电容增大能够提高系统的稳定性。

为验证负载功率大小对系统稳定性的影响，设定起始负载功率为20 kW，在t=1 s，负载突增至30 kW，在t=2 s，又进一步增大到50 kW，母线电压波形如图17 所示。

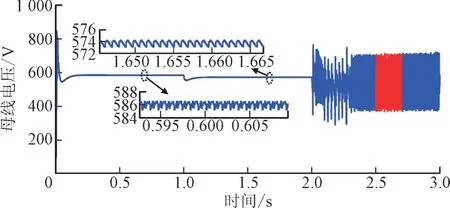
图17 负载功率变化时母线电压波形Fig.17 Bus voltage waveform with load power changing

由图17 可知，在式（14）所计算负载范围内，随着负载功率增大母线电压虽有一定的跌落，但仍旧能维持稳定。可当负载增大到50 kW 时，母线电压振荡加剧，由此得出负载功率超过临界值会加剧母线电压波动，不利于系统稳定，验证了前文所述结论。对负载功率增大到50 kW 时的母线电压波形（图17 中红色波形部分）进行快速傅里叶变换（Fast Fourier Transform，FFT），得到如图18 所示结果，当系统发生振荡时，振荡频率大约在77 Hz 左右，与图12（b）中阻抗不匹配对应频段基本吻合。

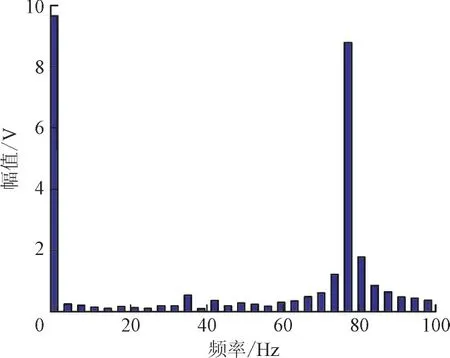
图18 负载50 kW时母线电压FFT分析结果Fig.18 FFT analysis results of bus voltage with load of 50 kW

图19 所示为系统带电阻性负载时的母线电压波形，电阻性负载功率为50 kW，母线电压存在一定程度的波动，但基本趋于稳定。而图17 中t=2 s 时接入50 kW 恒功率负载系统出现剧烈振荡，由此可知恒功率负载会降低系统稳定性。

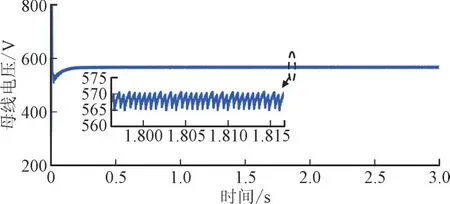
图19 直流微电网带电阻性负载时母线电压波形Fig.19 Bus voltage waveform of DC microgrid with resistive load

5 结论

本文针对光储直流微电网中变换器的多种控制方式和不同运行工况进行稳定性分析及仿真验证，得到以下结论：

1）通过建立微电网系统的模型，结合稳态分析与劳斯判据得出系统稳定时负载功率及母线电容的边界条件，其适用于多种工况，对系统设计具有指导意义。

2）利用基于BVCC 和BCCC 的通用稳定性判据对不同运行工况下系统的稳定性进行分析，得到适用于系统多工况运行的环路增益表达式，增强其使用通用性；同时，利用所得边界条件能够确定合适的负载功率及母线电容参数值，使系统在多工况运行时都能够维持系统稳定。通过Nyquist 曲线以及Bode 图分析得出工况1 的稳定裕度较小，并且验证了负载功率及母线电容的变化对系统稳定性的影响。

3）对光储直流微电网不同运行工况进行仿真，验证了边界约束条件及稳定性分析结论的正确性。