基于分布鲁棒联合机会约束的光储充电站滚动优化调控模型

孙 舟，王洪彪，肖万芳，王立永，袁小溪，胡泽春

（1.国网北京市电力公司，北京 100031；2.清华大学电机系，北京 100084）

0 引言

近年来，电动汽车充电负荷管理问题备受关注，随着新能源持续接入及充电需求的不断提升，光储充一体化充电站应运而生，其优势在于可以充分利用可再生能源生产电力，从而减少对传统能源的依赖，同时将多余的电能储存起来在系统需要时使用。光储充电站有望在未来成为一种重要的电动汽车充电解决方案，为清洁能源的发展做出贡献。

相较传统电动汽车充电站，光储充电站具有许多优势，如可靠性更高、电力成本更低、减少碳排放等[1-6]，近年来，世界各地对光储充电站已经进行了较多的试点和应用[7-13]，研究者除了使光储充电站具备基本的充电功能外，还将其应用于提升配电网的稳定性[14-15]、端对端（Peer-to-Peer，P2P）能源交易[16-17]、车网互动（Vehicle to Grid，V2G）[18-26]等方面。文献[27]建立了电动公交车光储充电站多场景日前优化模型，用场景集的方式考虑光伏出力的随机性，并在日内使用滚动优化策略对日前模型进行修正。文献[28]为解决混合整数优化计算时间较长的问题，提出考虑未来车辆的博弈模型，其博弈被证明收敛于纳什均衡。文献[29]认为预测误差会让优化调度求解的最优性受到挑战，提出将Lyapunov 函数优化方法用于电动汽车有序充电。文献[30]提出1 种新的度量标准来评估充电行为对电网的影响，其优点在于无需求解完整的潮流方程。文献[31]在考虑车辆随机到达和离开时间基础上，提出1 种基于实时价格的自动需求响应的充电策略。文献[32]采用日前调度和实时操作的两阶段能量管理方法，解决配建有光伏和电动汽车的办公楼宇能源调度问题。文献[33]针对天气变化可能对光伏出力造成的影响，提出1 种根据电价区间在基于优化思想与市场规则的优化运行模式。

综上所述，国内外学者对光储充电站的优化运行已有一些研究，也对光伏出力随机性提出了应对措施，但同时考虑新能源出力、基础负荷、电动汽车充电需求3 者随机性的研究还较少。本文研究的主要贡献包括：（1）考虑新能源出力、基础负荷、电动汽车充电需求的随机性，提出基于分布鲁棒联合机会约束（Distributionally robust joint chance constraints，DRJCC）的光储充电站滚动优化调度模型，并使用条件风险价值（Conditional Value at Risk，CVaR）对该问题进行了凸松弛；（2）针对基于混合整数规划（Mixed Integer Programming，MIP）的精确DRJCC 模型、基于CVaR-Slim 凸松弛的DRJCC 模型、基于Bonferroni 不等式的DRJCC 模型3 种模型进行比较，算例分析结果表明基于CVaR-Slim 凸松弛的DRJCC 模型在保守度上与基于MIP 的精确DRJCC模型相似，并且可显著加快求解时间；（3）考虑待接入充电车辆随机性的影响，提出自适应更新未来接入车辆充电功率场景的方法。

1 电动汽车充电的滚动优化模型

1.1 系统结构

本文研究考虑的应用对象为光储充一体化电站的充电运营商，其运营的充电站包括一定数量的充电桩、分布式光伏等新能源发电设备、储能系统。电动汽车用户存在充电需求时会将车辆接入充电桩，并设置预期离开时间和期望电量水平。充电运营商在配电变压器功率限制的情况下，根据分时电价、新能源发电出力、基础负荷、电动汽车充电需求等信息合理安排电动汽车充电功率计划，以最低运行成本满足用户的充电需求。光储充电站系统结构如图1 所示。

图1 光储充电站系统结构Fig.1 Structure of photovoltaic energy storagecharging station

1.2 基于事件触发的滚动优化方法

为实现电动汽车充电的实时调度，本文采用基于事件触发的滚动优化方法。该方法主要依据以下触发事件来执行，包括定时触发、电动汽车接入/离开、用户修改预期充电时间/电量、配电变压器容量达到限制等。当触发事件发生后，充电运营平台通过完成一系列操作来进行信息采集、功率预测、优化求解及指令发布，以实现站内能量优化调度。信息采集由充电桩和用户充电APP 负责实时采集上传，内容涉及当前接入车辆的电量水平、预计离开时间和期望电量；功率预测程序根据不同场景发生概率输出新能源出力预测曲线、基础负荷功率曲线、未来接入车辆功率曲线；优化求解程序根据以上数据，建立电动汽车充电实时调度基本优化模型，并计算该时段的车辆充电功率和储能系统功率；指令发布环节中，系统将调度指令发布至充电桩和储能单元，以执行相应的充电操作。基于事件触发的滚动优化方法流程示例如图2 所示。

图2 基于事件触发的滚动优化方法流程示例Fig.2 Process example diagram of event-triggered scrolling optimization method

1.3 电动汽车充电实时调度滚动优化模型

为综合考虑充电运营商成本与用户充电体验，建立目标函数由充电运营商购电成本、充电电量偏离预期惩罚、充电滞后惩罚组成的电动汽车充电实时调度滚动优化模型表达式为：

电动汽车充电实时调度基本优化模型需要满足如下约束条件。

1）充电过程约束为：

2）充电桩充电功率约束为：

充电桩只在其有电动汽车接入的时段内有输出功率，其充电功率约束表达式为：

式中：Pi,max为第i个充电桩的最大充电功率，其值为所接入电动汽车电池能够允许的最大充电功率和充电桩最大功率中的较小值。

3）储能运行约束为：

4）功率限制约束为：

2 基于分布鲁棒联合机会约束的光储充电站实时调度模型

2.1 分布鲁棒联合机会约束

鲁棒优化在确保随机变量所有可能取值均符合约束条件时可能过于保守。机会约束优化通常涉及对历史数据样本进行分析，通过聚类等方法提炼出场景集以估计随机变量的真实概率分布，但其概率分布的估计误差可能会对优化结果产生较大影响。本文提出一种分布鲁棒联合机会约束优化方法，可以解决鲁棒优化和机会约束优化存在的问题。

将含有随机变量的约束式（9）—式（11）简化为：

为方便后续描述，设该约束集共有nopp条机会约束，则第k个（其数量等价于对应常系数矩阵及常数向量的行数及个数）机会约束为：

式中：ak为常系数矩阵A的第k行系数；bm为常系数矩阵B的第m行系数；cl为常数向量C的第l个常数值；nopp为机会约束总数。

由于式（12）—式（13）的约束中带有随机变量，而充电计划需在随机变量明确之前进行决策，所以无法直接采用确定性方法求解。解决该问题通常使用的方法有鲁棒优化、机会约束优化、分布鲁棒联合机会约束优化方法。

1）鲁棒优化。首先确定随机变量的不确定集U（根据描述问题的不同，通常将其划分为区间集、椭球集或多面体集），将计算转换为其鲁棒对等形式，变成1 个确定性问题来解决。即在所述不确定集合的所有可能取值情况下，都必须满足约束条件为：

式中：U为随机变量的不确定集。

2）机会约束优化。在获取了随机变量的概率分布Pran后，通常用机会约束描述式（12）—式（13）。独立机会约束是指在给定的概率下满足单个约束，其机会约束优化表达式为：

式中：αk为第k个机会约束的置信度。

考虑各约束之间的相关性，需要建立联合机会约束。联合机会约束要求nopp个内部约束同时成立的概率不小于给定的置信度，其表达式为：

式中：Z(·) 为机会约束函数；α为任意给定的置信度。

3）分布鲁棒联合机会约束优化方法。其目的是让式在指定观测概率分布附近的分布集合中均成立，此处的分布集合被称为“模糊集”。构造模糊集的方法较多，本文采用Wasserstein 距离来构建分布鲁棒联合机会约束为：

2.2 基于MIP的精确DRJCC模型

式中：λ，ζ均为全局决策变量；sω，γω均为第ω个场景的辅助决策变量；为观测到的第ω个场景的随机变量；M为给定的任意大正数；yω为第ω个场景的辅助0-1 决策变量；‖·‖*为对偶范数，与Wasserstein 距离定义中的范数相对应。

2.3 基于CVaR-Slim凸松弛的DRJCC模型

采用CVaR 对约束进行凸近似，即：

式中：vω,k为第ω个场景中第k个机会约束的向量。

2.4 基于Bonferroni不等式的DRJCC模型

采用Bonferroni 不等式近似分布鲁棒联合机会约束为：

2.5 各分布鲁棒联合机会约束模型对比

基于2.2 节—2.4 节分析，可得到基于MIP 的精确DRJCC 模型、基于CVaR-Slim 凸松弛的DRJCC模型、基于Bonferroni 不等式的DRJCC 模型（简写为MIP、CVaR-Slim、Bonferroni 模型）。用O(·)函数描述上述3 种模型在求解过程中的模型复杂度，各分布鲁棒联合机会约束模型复杂度如表1 所示。

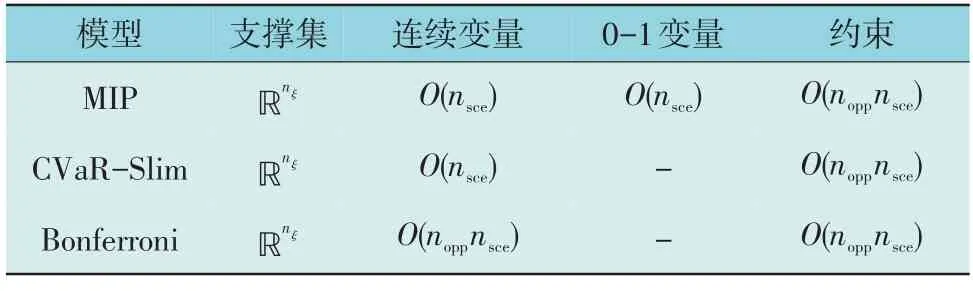
表1 各分布鲁棒联合机会约束模型复杂度Table 1 Complexity of DRJCC model for each distribution

在MIP 模型中，尽管模型转换是等价的，但由于默认支撑集为整个实数域，使得模型相较于原支撑集更为保守。在CVaR-Slim 模型中，同时对支撑集和模型转换进行了近似，因此比MIP 模型更为保守。在Bonferroni 模型中，由于其会对每个独立机会约束做CVaR-Slim 近似，然后用一个保守的Bonferroni 不等式将独立约束结合在一起，所以相较于CVaR-Slim 模型更加保守。

3 算例分析

3.1 参数设置

以某居民区光储充电站为仿真测试对象，站内包含50 kW 分布式光伏、150 个充电桩、储能容量为200 kWh 功率为200 kW 的储能设备，配电变压器容量为1 000 kVA。为建立充电需求样本集，参考美国国家公路交通安全管理局（National Highway Traffic Safety Administration，NHTS）发布的燃油车出行统计数据。由于家庭传统燃油车的出行规律与家庭电动汽车的出行规律存在相似性，因此这些燃油车的出行数据可以作为建立电动汽车充电需求样本集的参考。通过分析这些数据，可以了解家庭的出行模式、行驶距离、出行时间等，从而有助于预测电动汽车的充电需求。电动汽车到达/离开时刻概率密度分布如图3 所示。

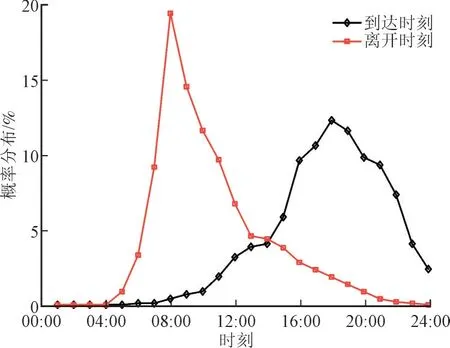
图3 电动汽车到达/离开时刻概率密度分布Fig.3 Electric vehicle arrival/departure time probability distribution

采用蒙特卡洛抽样法，根据到达和离开时刻随机抽选电动汽车样本。计算每天抽取100 辆充电车辆的到达与离开时刻样本数据，得到电动汽车充电功率在7～15 kW 之间、电池容量在30～70 kWh之间。基础负荷、光伏出力数据均选用实际的基础负荷与光伏出力数据，将基础负荷的平均值归一化为800 kW，光伏出力的平均值归一化为20 kW，购电电价使用北京工商业分时电价，售电电价为0.9倍的购电电价。另外，为了反映变压器具备短时间的容量超载能力，在变压器的约束式—式中增加松弛变量，并在目标函数中对该松弛变量进行惩罚。

仿真中的时间间隔为15 min，储能设备的充电与放电效率均为0.95，在分布鲁棒机会约束中θ=0.1,α=0.3。目标函数中充电偏离预期惩罚系数σ取值为最大购电价格的2 倍。仿真程序使用Python 语言编写，模型用CVXPY 描述，MIP 模型、CVaR-Slim 模型、Bonferroni 模型均符合参数化规划规范（Disciplined Parametrized Programming，DPP），在CVXPY 中可以进行预编译以提升求解速度。

3.2 算例仿真结果

为预测未来将接入车辆对电网的影响，在运行滚动优化计算时，统计1 周内在当前时间点之后到达车辆所产生的充电需求。采用逐个迭代的方式，将这些待接入车辆的充电功率加入到场景集中。在每个优化时间点，场景集由1 周内的待接入车辆充电功率、基础负荷以及通过聚类分析生成的典型光伏出力共同构成。对该光储充电站连续2 天的运行功率进行仿真计算，考虑和不考虑未来接入车辆影响的光储充电站充电功率及购电电价曲线如图4 所示。

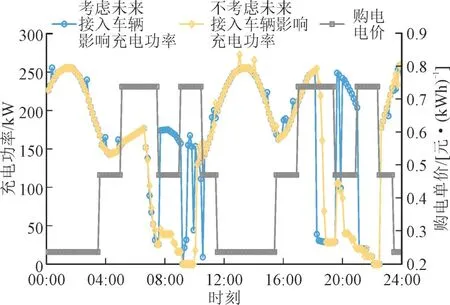
图4 光储充电站充电功率及购电电价曲线Fig.4 Charging power and electricity purchase price curve of photovoltaic energy storage-charging station

由图4 可知，在不考虑未来接入车辆影响的情况下，优化模型总会对当前充电车辆给出最经济的充电计划，即将所接入车辆均安排在电价最低时段进行充电。但实际上未来接入车辆会对该种“贪婪”策略造成很大的影响，如第1 d 下午15：00—20：00到达车辆的充电需求被转移至第1 d 晚23：00 后充电，即转移至谷电价时段充电，但由于当天20：00后新接入了较多的电动汽车，导致23：00 后变压器达到容量上限，无法满足所有车辆的充电需求。在考虑未来接入车辆影响的情况下，当接收到第1 d下午15：00—20：00 的车辆信息时，由于在历史记录中发现在20：00 后才到达车辆的充电需求基本会被转移到晚23：00 后充电，所以当前时刻接入的车辆会被安排及时充电，即在15：00 到达时刻就开始充电，从全局来看可以满足更多车辆的充电需求。在本算例下，考虑未来接入车辆影响后，可以额外满足11.46%的车辆充电需求。

3 种分布鲁棒联合机会约束模型下算例仿真结果如图5 所示。由图5 可知，优化程序针对充电功率输出进行了改进，能够自动降低充电功率，有效解决了预测误差引起的变压器容量超限问题。Bonferroni 模型因其保守性最高、充电功率最小，可确保充电功率、基础负荷、光伏发电和电池充放电的总和不会超过变压器的容量限制。CVaR-Slim 模型次之，而MIP 模型则是最不保守的。Bonferroni和CVaR-Slim 模型的求解时间小于0.1 s，MIP 模型的求解时间在1 s 内。由于MIP 和CVaR-Slim 模型的保守性较低，导致变压器可能会因预测误差而超载。因此，需要动态监控变压器的实时负载功率，以防止过载情况。而Bonferroni 模型由于其较高的保守性，在此算例中没有出现因变压器容量限制而需要削减充电功率的情况。

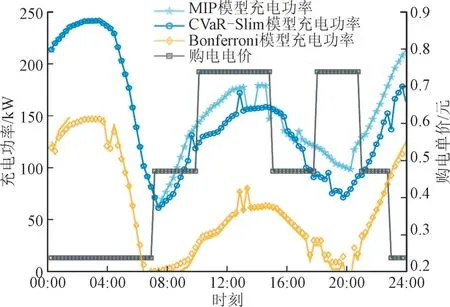
图5 3种分布鲁棒联合机会约束模型下算例仿真结果Fig.5 Simulation results of examples with three DRJCC models

对比图4 和图5 可知，确定性优化产生的充电功率波动较大，尽管能容纳更多车辆，但由于未考虑充电随机性，仍存在不能满足车辆充电需求的情况；而在基于CVaR-Slim 凸松弛的DRJCC 模型中，由于其所具有的保守性导致允许接入的车辆数量变少，车辆的充电需求均能够被满足，功率曲线也较为平稳。

4 结语

本文针对电动汽车随机接入影响下光储充电站功率难以精准调控的问题，提出基于DRJCC 的光储充电站滚动优化调控模型。算例分析表明，基于MIP 的精确DRJCC 模型和基于CvaR-Slim 凸松弛的DRJCC 模型二者的优化结果更为接近；由于不含0-1 变量，基于CVaR-Slim 凸松弛的DRJCC 模型的求解时间更短；基于Bonferroni 不等式的DRJCC 模型由于运行过于保守，导致较高比例的车辆充电需求没有得到满足；在变压器容量不足的场景下，考虑未来接入车辆影响可以将电动汽车充电满足率提升10%以上。在后续的研究中，将进一步完善优化目标函数，增加考虑光储充电站运行的低碳性及经济性，丰富所提模型的应用场景。