基于腱绳驱动的仿人灵巧手

刘阳，江励，徐俊佳，汤健华

（五邑大学 智能制造学部，广东 江门 529020）

0 引言

仿照人手生物学结构设计的仿人灵巧手有很高的灵巧性、通用性和适应性，能够完成多种抓取和操作任务。当前具有拟人特征的灵巧手按照仿生结构设计划分，可以划分为机械式铰链结构、仿生生物关节、腱绳驱动结构等类型[1]。

机械式铰链方式设计的灵巧手，如SCHUNK S5FH[2]、KITECH-Hand[3]，手指内采用齿轮、连杆等传动机构。SCHUNK S5FH以9个独立的伺服电动机来控制21个自由度，其手指间采用连杆结构耦合，多根手指一同进行屈伸和侧摆运动。

仿生生物关节结构设计的灵巧手模仿动物骨骼并仿人化。具有代表性的是FLLEX Hand[4]，拥有15个自由度，质量仅有1.81 kg，它的关节结构、运动方式、驱动传动布置乃至润滑方式都极力模仿人手的构造，实现了良好的运动灵活性，为多指灵巧手的深度仿生研究开辟了崭新的思路。

腱绳驱动结构是模仿动物肌腱传动的结构，需要滑轮或绕线机构以实现腱绳的收放，因此有结构尺寸过大的问题。于是一种利用柔性腱绳在扭绞过程中缩短效应的Twisting Wire Actuator驱动器[6]被研制出来，UB Hand[5]是具有代表性的采用扭绞腱绳驱动结构的多指灵巧手，该灵巧手利用Twisted-string Actuation System[7]作为它的驱动系统。

上述各类产品对灵巧手的设计奠定了基础，但是手指耦合运动一般采用连杆结构，对加工精度要求高，较难实现类似人手的灵活程度和操作能力。本文提出了一种仿人灵巧手的结构设计方案：将腱绳缠绕减速与腱绳传动相结合，采用特殊绕绳方式实现手指的侧摆和耦合运动，完成了灵巧手仿生、紧凑、轻量化的设计，所设计的灵巧手具有类人的灵巧和抓取力。

1 灵巧手的设计

1.1 灵巧手整体结构

参考人手的生理结构，选择和仿照人手的功能特征进行灵巧手的设计。灵巧手的三维图如图1所示。针对集成和尺寸方面的问题，本文采用了缠绕绳驱动模式作为灵巧手的驱动源，灵巧手的驱动模块如图2所示。

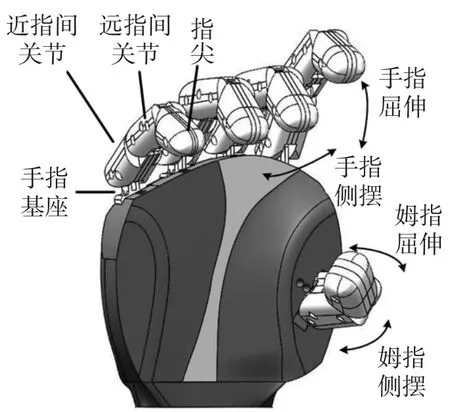
图1 灵巧手及其结构简图

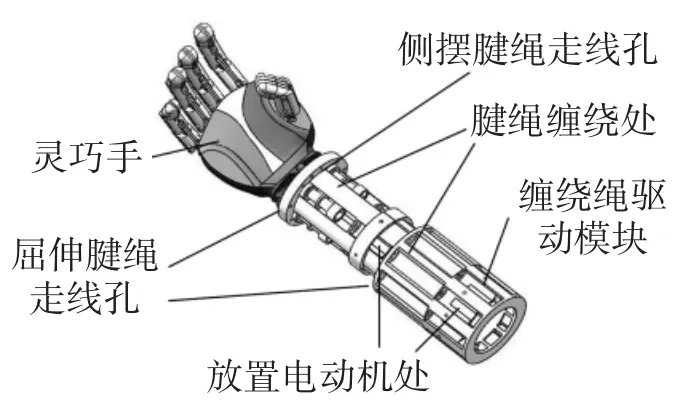
图2 灵巧手驱动模块

最终本文所设计的灵巧手满足以下要求：1）灵巧手的整体大小与人手相似。2）灵巧手结构与人手相似，具有人手的运动特征。每根手指包含3个关节，且都具有3 个独立可控的自由度，其中基关节有2个自由度，分别为屈伸自由度和侧摆自由度，手指侧摆关节角的运动范围为-20°～20°，手指弯曲/伸展的关节角运动的范围均为0°～90°。3）灵巧手功能方面具有体积小、质量轻、抓取速度快及抓取力大的特点。采用了缠绕绳驱动模块，模仿人手的肌腱传动，使灵巧手手指依靠腱绳的拉动实现运动。

1.2 灵巧手的手指结构设计

本文采用模块化设计的思路，灵巧手的每根手指结构相同，长度不同，便于制造和维护。灵巧手手指建模如图3所示，手指有4个部分：指尖、指中、指根和手指基座。

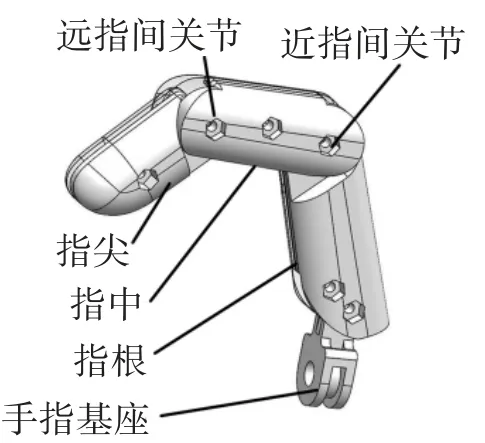
图3 手指结构三维图

人手每根手指的远指间关节（DIP）和近指间关节运动（PIP）都具有耦合性，且DIP运动的角度约等于PIP运动角度的2/3[8]。本文用腱绳仿照人手的斜形韧带，采用一种特殊绕绳方式，绕绳方式如图4（a）所示，绕绳原理如图4（b）所示，T1、T2、T3、T4为 指尖、指中、指根和基座；R1、R2圆代表手指的DIP关节和PIP关节；L1为DIP关节和PIP关节耦合的传动绳，L2、L3为灵巧手手指的屈伸传动绳。L1始于T1绑绳处，绕R1、R2后绑于T3绑绳处，L2、L3分别绑于T2、T3绑绳处；腱绳L1可以分为5段，其中t1、t2与R1、R2相切，t3同时与R1、R2相切。K为DIP关节圆心到T1绑绳处的距离，RR1为DIP关节圆半径。

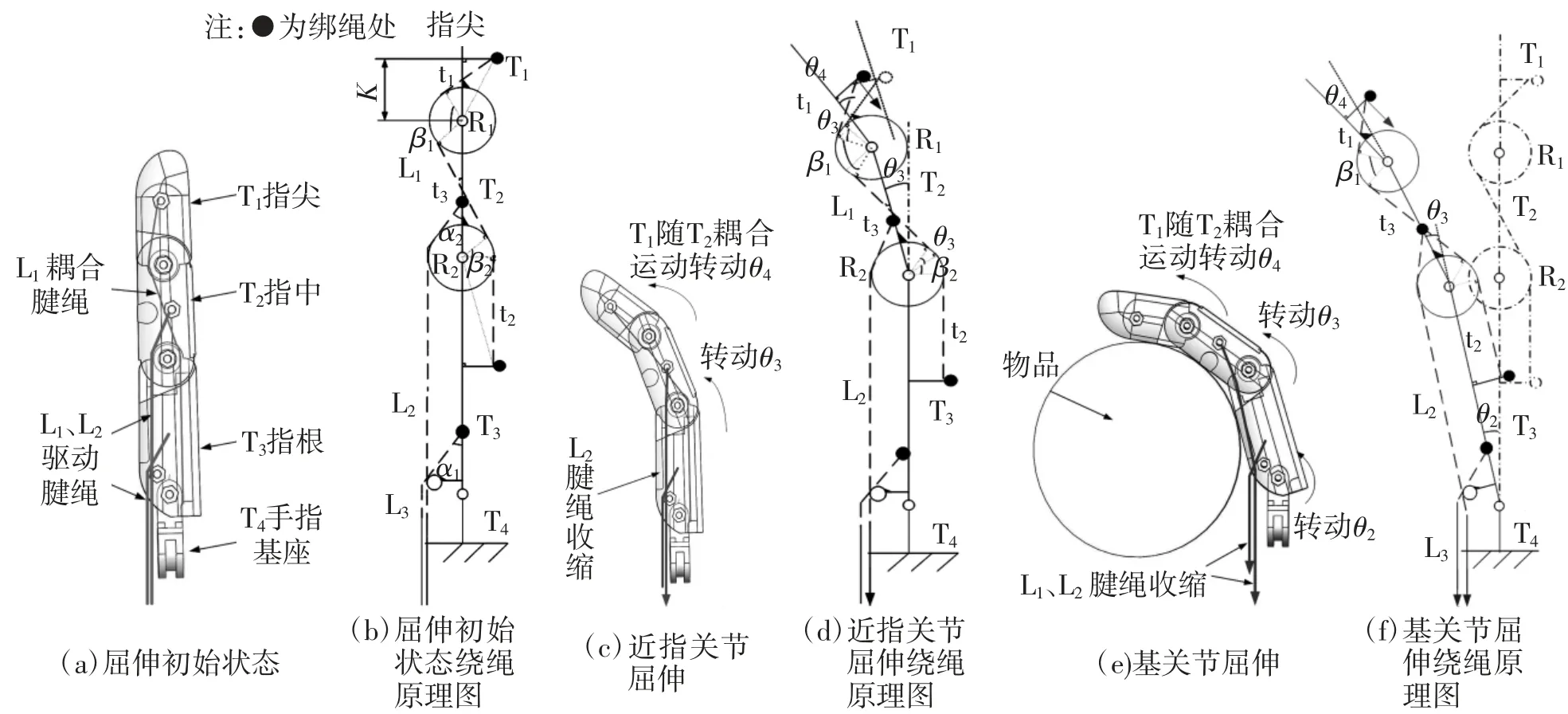
图4 手指绕绳图及其原理图

当腱绳L2段缠绕收缩时，手指三维图如图4（c）所示，其传动原理如图4（d）所示，腱绳L1长度不变且保持拉紧状态，当指中T2受到腱绳L2的拉力并转动θ3时，腱绳L1绕R1、R2的β1与β2段相对滑动。腱绳L1的t1段拉动指尖T1绕着R1的轴转动θ4。θ3与θ4满足以下关系式：

只需保证K和RR1的比例关系，远、近指间关节即可有类人的耦合运动特征，可以更好地贴合物品。

当腱绳L2段和L3段缠绕收缩时且被抓取物品位于灵巧手抓取空间内，手指三维图如图4（e）所示，传动原理如图4（f）所示，手指部位T2、T3受到腱绳L2、L3传动力，绕着R2、R3的轴转动θ2、θ3。

1.3 灵巧手的驱动设计

1.3.1 缠绕绳驱动器设计

利用腱绳在扭绞缩短效应，确定一种缠绕绳驱动方案，实现运动和动力的同步传递。如图5所示，将平行放置的相同半径的腱绳一端与电动机输出轴相连，另一端与待驱动物体相连，通过电动机输出轴扭转一端的柔性腱绳，使另一端的腱绳线性收缩以实现对手指的驱动。缠绕绳驱动器可灵活布局腱绳的走线，大大简化了结构设计和尺寸空间，腱绳具有一定的弹性，也为手指运动提供了一定的柔顺性和适应性，并且驱动方式具有极高的减速比，使得它可以采用微型直流电动机作为原动机。

图5 缠绕绳驱动系统

1.3.2 灵巧手手指侧摆设计

手指侧摆机构采用一种特殊的绕绳方式：腱绳穿过缠绕轴，绑于侧摆机构两端且始终保持紧绷状态。当手指处于初始位置，腱绳绑于侧摆机构左侧后，预缠绕于缠绕轴段为S1段，腱绳从缠绕轴A口穿入，从B口穿出，从缠绕轴B口出来后绑于侧摆机构右侧为S2段（如图6（a））。

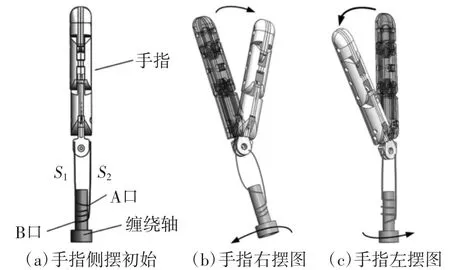
图6 手指侧摆示意图

当电动机向左转时，S2段越缠绕于缠绕轴，而S1段解缠绕，相当于侧摆机构右侧受到拉力，左侧放松，此时手指向右侧摆动（如图6（b））。当电动机向右转时，S1段越缠绕于缠绕轴，而S2段解缠绕，相当于侧摆机构左侧受到拉力，右侧放松，此时手指向左侧摆动（如图6（c））。侧摆机构响应速度快且在灵巧手内部所占的空间小。虽然输出力相对较小但是也符合人手侧摆方向的特性。

1.4 灵巧手控制系统

为验证灵巧手的灵巧性和实际抓取能力，进行了灵巧手控制系统的搭建。灵巧手的控制系统最主要为完成以下几种任务：电动机转速、电流和角度控制，灵巧手运动学计算，传感器信号的采集和处理。灵巧手的控制系统简图如图7所示。

图7 灵巧手控制系统简图

控制系统以STM32主控芯片作为系统的总控单元，采用15个微型直流电动机作为原动机。由电动机内的霍尔传感器得到电动机角度，再通过运动学计算间接测量手指关节转角。电动机驱动器选用Robomodule-rmds-108直流电动机驱动，通过CAN总线与主控芯片STM32通信。

使用QT上位机开发图形界面库，开发灵巧手的上位机控制软件。上位机软件的主要功能包括读取、设置各电动机角度、速度、电流与STM32主控芯片进行串口通信发送指令等功能。上位机的界面如图8所示。

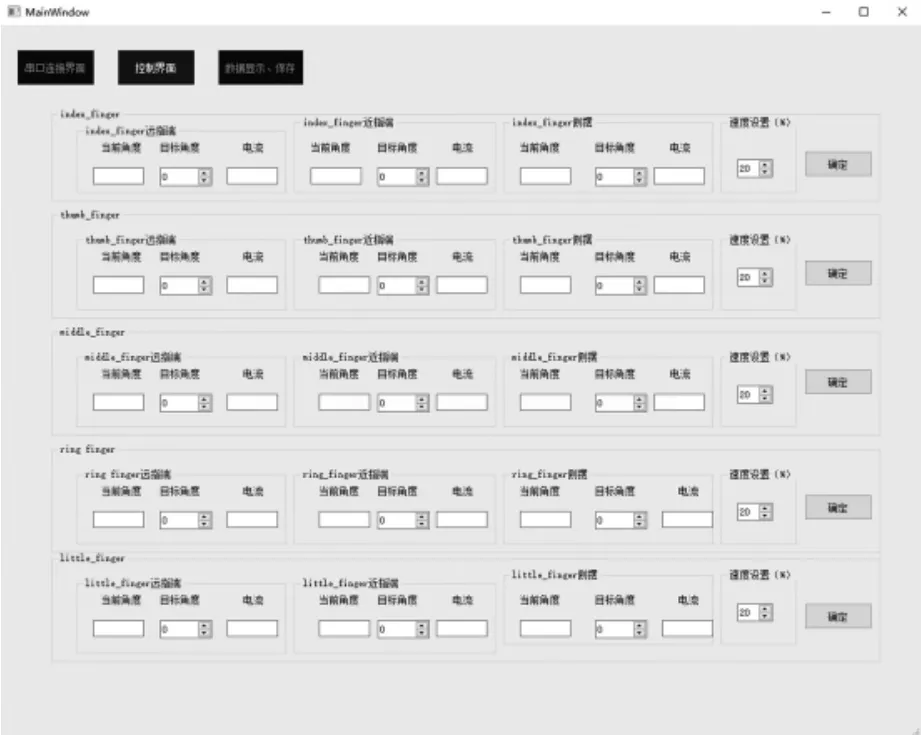
图8 上位机控制软件界面

2 灵巧手的运动学分析

2.1 驱动器运动学

2.1.1 缠绕绳驱动运动学

缠绕绳驱动运动学模型是在对缠绕后的腱绳进行几何展开的基础上建立的。如图9所示，S1段与S2段的和为腱绳的初始长度，并假设其在整个缠绕过程中保持不变，D为绳索输出点到缠绕后腱绳的轴心线之间的距离，β为腱绳缠绕的螺旋角，r为腱绳的缠绕半径（在这里其值等于腱绳的半径），当电动机的转角为ε时，腱绳的收缩长度ΔL计算公式为

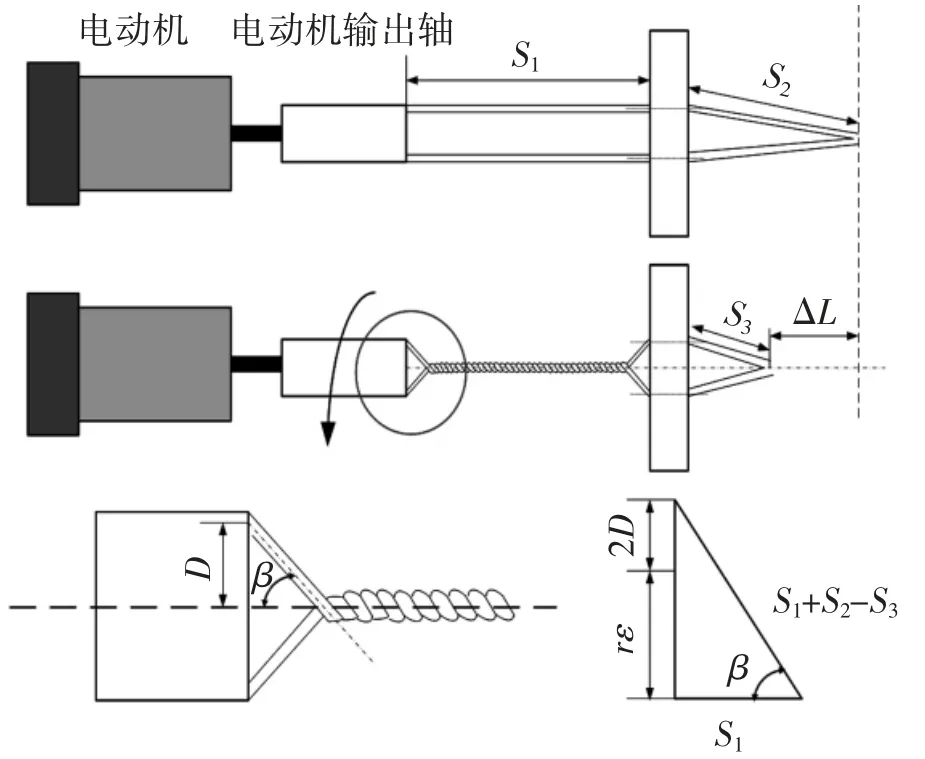
图9 驱动器运动学图

因腱绳的长度在整个缠绕过程中保持不变，S3计算公式为

把式（3）代入式（2），得到电动机的转角为ε与腱绳收缩长度ΔL的关系式为

腱绳收缩长度ΔL与手指关节转角θ关系式为

式中：c为收缩腱绳绑绳处到手指旋转关节距离。

2.1.2 灵巧手手指侧摆运动学

图10中：β为腱绳缠绕的螺旋角，r为腱绳的半径，R为缠绕轴的半径，2T为手指底座长度，当电动机的转角为ε时，侧摆机构一侧放松，一侧受到拉力，侧摆机构绕其旋转中心旋转，缠绕于缠绕轴的长度的增加量与侧摆机构旋转的弧长相等，关系公式如下：

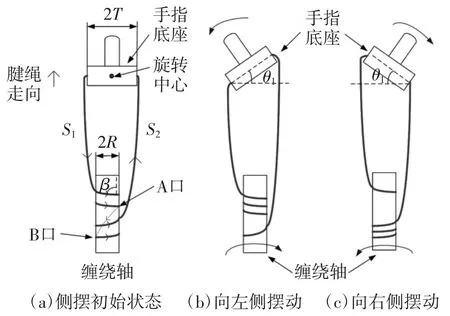
图10 手指侧摆运动学图

式中，θ1为手指侧摆动的角度。

2.2 灵巧手手指的运动学分析

2.2.1 灵巧手手指正运动学分析采用经典的D－H法进行运动学分析，建立坐标系（如图11）和对应的D-H参数表（如表1），其中：{O0-X0Y0Z0}为旋转基关节上的原始坐标系，{O1-X1Y1Z1}、{O2-X2Y2Z2}、{O3-X3Y3Z3}分别为掌指关节、第二指间关节及第一指间关节的坐标系，{O4-X4Y4Z4}为指尖末端的坐标系；ai为连杆长度；αi为连杆扭转角；di为两连杆距离；θi为关节转角。

表1 手指D-H参数表

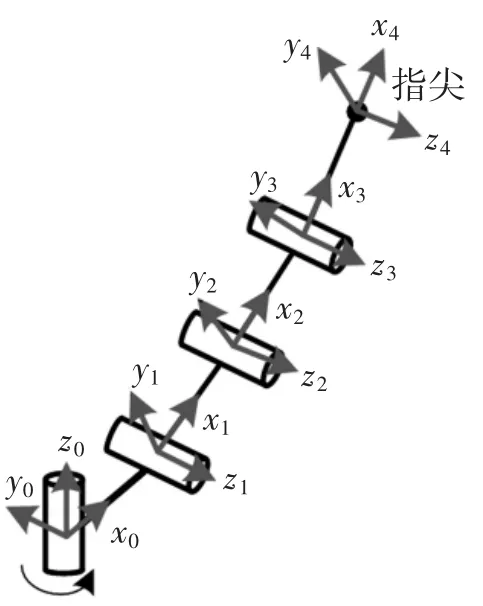
图11 手指连杆坐标系

根据D-H参数法，每个旋转关节都可以用如下的齐次变换矩阵描述：

式中：Si=sin θi；Ci=cos θi；Sij=sin（θi+θj）；Cij=cos（θi+θj）；Sijk=sin（θi+θj+θk）；Cijk=cos（θi+θj+θk）。

给定灵巧手指的关节角θ1～θ3（θ3与θ4有耦合关系）即可确定指尖在基座标中的空间位置坐标（0X4，0Y4，0Z4）：

根据上一节驱动器运动学公式（5）、公式（6），可得θ1～θ3与分别控制手指关节角θ1～θ3的电动机转角ε1～ε3的关系：

再代入式（9）～式（11）可得电动机转角ε和指尖在基座标中的空间位置坐标（0X4，0Y4，0Z4）。

2.2.2 灵巧手手指逆运动学分析

（0X4，0Y4，0Z4）为已知的指尖坐标系原点在基坐标系中的坐标，由于所求为3个关节转角，故不需要知道指尖的姿态也可完成逆运动学求解。

由简单的几何关系可以得到侧摆转角θ1：

记A=0X4/C1、B=0Z4，由式（11）可得

移项可得

利用数值法对式（15）进行求解，可得出θ3，而θ3与θ4有耦合关系，根据耦合关系可以求得θ4。

由式（11）有0Z4=a4S234+a3S23+a2S2，可拆分为

其中：H=a2+a3C3+a4C34；K=a3S3+a4S34。

由式（18）可求得θ2：

根据式（12）～式（14），通过θ1、θ2、θ3反求得分别控制手指关节角θ1至θ3的电动机转角ε1、ε2、ε3的值：

2.2.3 灵巧手手指的工作空间

灵巧手工作空间指的是指尖所能到达的区域，区域的大小可以衡量手指的工作能力和性能。

以食指为例，在Matlab中的Robotics Toolbox工具箱中，根据表1建立手指模型，在关节转角取值范围内随机取30 000组关节角度θi，得到指尖参考点全部随机位置组成的点云空间，即手指的工作空间（如 图12），可以看到手指的工作范围是由各个关节的长度和关节可旋转的角度来决定。所设计的手指灵活的姿态角度变化有利于抓取形状复杂且不同的目标物体，较大的位置范围有利于抓取大小不一的目标物体。

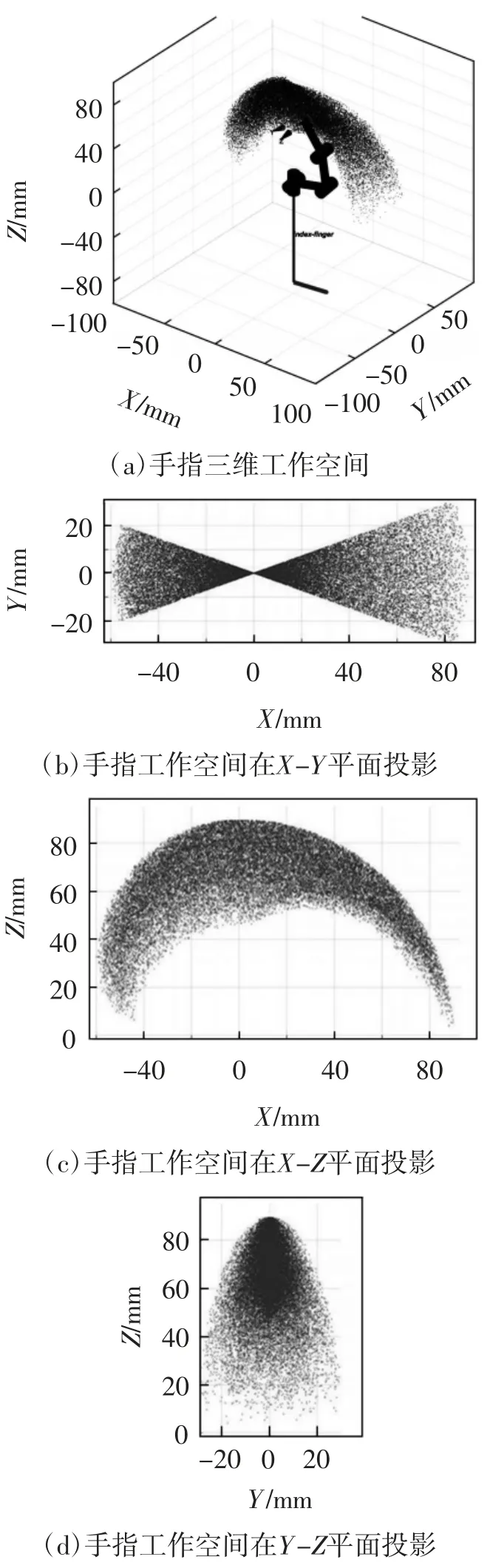
图12 灵巧手手指的工作空间

2.3 灵巧手手指静力学分析

灵巧手的静力学是研究手指在各个方向的力都平衡的状态下，灵巧手关节驱动力矩与指尖受力的关系。

为进一步简化研究问题，本文只分析屈伸方向的静力学，当灵巧手在抓取时，可将手指和被抓物体视为刚体，并假定被抓物体与每个手指指节间的接触为单点接触。图13所示的灵巧手手指，要产生图13（a）所示的虚位移，图13（b）为灵巧手指接触物品时各力之间的关系式。

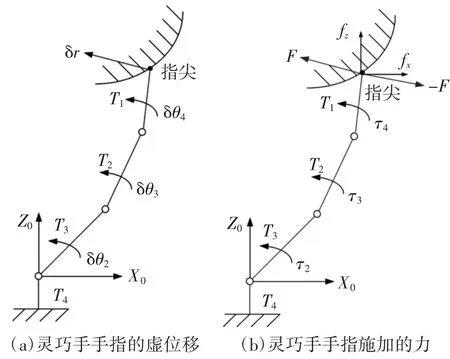
图13 灵巧手手指的虚位移和施加的力

根据式（1）、式（9）、式（10）手指的运动学方程，对角度θ进行微分计算，可以得到手指的雅可比矩阵：

式中：Sij=sin（θi+θj）；Cij=cos（θi+θj）；Sijk=sin（θi+θj+θk）；Cijk=cos（θi+θj+θk）。

代入τ=JTF，由此可得到关节驱动力矩与指尖力间的关系：

式中：fx和fz为指尖力在x、z方向的分力，N。

3 灵巧手的抓取试验

灵巧手实现动作时，对应手指的腱绳在内置驱动电动机作用下缠绕收缩，实现手指的弯曲；复位时驱动电动机带动腱绳归位，同时在回复力弹簧作用下恢复到原位置。

五指灵巧手可完成如图14（a）、图14（b）、图14（c）所示的动作。试验表明，该五指灵巧手具有高度的仿人手特点，每根手指能够独立运动并互相配合。五指的侧摆动作使五指灵巧手增大了灵活性和整手的工作空间，能够完成类人手的动作。

图14 灵巧手抓取试验

对灵巧手进行抓取试验验证，抓取以手指捏取和包络抓取最能反映灵巧手抓取性能。图14（d）、图14（e）、图14（f）是手指捏取试验，大拇指和食指作为灵巧手重要的手指之一，食指侧摆的范围增加可以提高食指的灵活性，两指与三指配合能够精确地抓取小球（直径为40 mm、质量为4 g）、小方盒（长为66 mm、宽为37 mm、高为15 mm、质量为50 g）等日常物品，通过试验可以看出，本文所设计的灵巧操作手能够实现对较小物体的捏取；图14（g）、图14（h）、图14（i）是包络抓取试验，抓取橙子（直径约75 mm、质量约为250 g）、订书机（不规则物品、质量约为120 g）、矿泉水瓶（直径约为60～65 mm圆柱体、质量约为550 g）。通过试验可以看出，不仅可以抓握常规物体，还可以抓握不规则物品。手指腱绳驱动具有自适应性且手指的远指端和近指端具有耦合的特征，使灵巧手贴合在物品表面，提高了抓取的类人灵巧性、适用性和稳定性。

4 结语

通过对人手的结构和运动特征进行分析，利用柔性扭绞腱绳作为灵巧手的传动方案，研究灵巧手腱绳传动方式下的结构，使手指内部空间得到解放，为后续传感器的安装带来了便利，实现了灵巧手仿生、结构紧凑、便于制造和维护的设计。对灵巧手手指运动学、静力学和工作空间分析，为灵巧手后续力的控制研究打下了基础。进行不同尺寸物体的抓持试验，从试验结果可知，该灵巧手具有较强的抓握能力和灵巧性，适用于工业机器人多用途末端执行器、人形机器人等对灵巧手的灵活性有较高要求的场合，为灵巧手的发展及应用提供了重要技术参考和研究思路。