基于近端算法的DC规划解球面约束下四次型极小化问题
2024-04-22舒杭,王洁
舒 杭,王 洁
(1.杭州电子科技大学理学院,浙江 杭州 310018;2.中国计量大学理学院,浙江 杭州 310018)
0 引 言
四次型极小化问题是张量逼近和多项式优化的交叉部分,是一类特殊的多项式优化问题。此问题有很多来源,并且在实际中有着广泛应用,许多实际问题的模型可表达为此形式,如图的稳定集问题、四阶张量的最佳秩一逼近问题、量子物理中的几何度量、光谱超图理论、扩散峰医学成像等。Aittomaki等[1]考虑波束优化问题并将其建模为多元四次型极小化模型。Aubry等[2]通过优化取实值的四次极小化模型来求解雷达信号问题。Mariere等[3]提出四次多项式优化模型并将其应用于数字通信的研究。
对于球面约束下的四次型极小化问题,可使用扩展的数值线性代数中的方法,例如对称移位高阶幂法(SS-HOPM),并且可以建立这种方法的良好性质。然而,采用一般非线性优化技术无法得出计算解的质量。特别是,我们无法判断计算解的全局最优性。对于能判断解的最优性的SDP松弛方法,却无法处理大规模问题。因此,我们对问题进行一些转化,使得重构后的问题变为两个凸函数的差的形式,此时就能采用DC算法来求解。但是该算法子问题的难度很大程度上取决于DC分解的选择,一般情况下子问题还需要借助于其他算法来求解,比如加速近端梯度(APG)算法,这也是DC算法的一个缺陷。我们根据近端算法,对DC算法进行一定改造,使得可以在DC算法的外框架上使用APG,简化子问题的求解,使得子问题不再需要借助于其他算法,我们将该方法根据加速方案的选择分别记为pDCA和aDCA。实验结果表明,此方法相较于对称移位高阶幂法和一般的DCA方法,在计算时间以及解的质量方面都得到了很大的提升。
1 问题描述及转化
张量是基于标量和矢量向更高维度的推广,标量和矢量都是张量的特殊情况,即标量和矢量分别是零阶张量和一阶张量。



(1)



s=i1+(i2-1)n,t=i3+(i4-1)n。
(2)
再将变量从向量转化为矩阵。令X=xxT,此时目标函数等价于〈AX,X〉。此时约束条件中还有变量未进行变换。
定理1[5]令x∈Rn,则集合
U={x|x∈Rn,xTx=1}
等价于集合
V={X|X=xxT,X≥0,〈I,X〉=1,rank(X)=1},
其中〈I,X〉=trace(X),X≥0表示矩阵为半正定矩阵,rank(X)表示为X的秩。
根据定理1,我们可以将对x的约束条件转化为对X的约束条件。此时问题形式如下:
min〈AX,X〉 s.t.X≥0, 〈I,X〉=1,rank(X)=1,
(3)

(4)
因为矩阵A是n2×n2的实对称矩阵,则可将矩阵A对角化,对应的正交矩阵设为Q。形式如:A=QTΛQ,其中Λ是由矩阵A特征值构成的对角矩阵。显然我们能将Λ拆分为两个正定的对角矩阵的差的形式,即Λ=Λ1-Λ2。设B=QTΛ1Q,C=QTΛ2Q。则〈AX,X〉=〈BX,X〉-〈CX,X〉。此时问题(4)的求解与以下问题的求解是等价的:
(5)
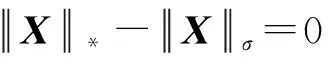
(6)
(7)

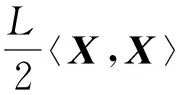
最终问题(7)等价于:
ming(X)-h(X) s.t.X∈Rn×n,
(8)
我们记P(X)=g(X)-h(X),那么P(X)即为所求目标函数。

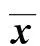
2 pDCA以及aDCA
对于优化问题ming(X)-h(X),DC算法的一般迭代格式是在每一次迭代的过程中利用次微分对目标函数的凹部分进行线性近似,从而得到一个目标函数的凸近似。即:
其中λt∈∂h(Xt)。
对问题(8)使用以上迭代形式,此时我们得到pDCA的子问题形式为:

(9)

基于以上讨论,现在给出pDCA的主要步骤:

Input:给定一个四阶实对称张量,选定初始点X0∈Ω,并设置X-1=X0输入惩罚参数,{βt}⊆[0,1); for t=0,1,2,… 取ξt=2CXt+ρΓt,Γt∈∂Xtσ, 令Yt=Xt+βt(Xt-Xt-1), Xt+1=argminX∈Rn×n<2BYt-ξt,X>+L2X-Yt2+δΩ(X) =PΩYt-1L[2BYt-ξt] , end for

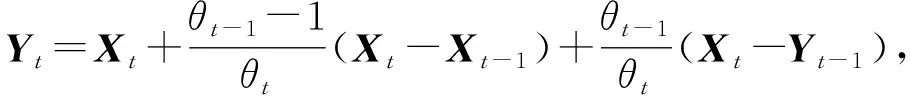
3 收敛性分析
定理3[9](全局子序列收敛性){Xt}为pDCA算法生成的序列,则以下陈述成立:
(1)序列{Xt}有界。
(3)序列{Xt}的任意聚点都是P(X)的稳定点。
命题1设{Xt}为pDCA算法生成的序列,则以下陈述成立:
(2)设{Xt}聚点的集合为N,则函数P在集合N上恒为μ。
证明注意到Xt+1是一个强凸函数的全局极小值点,根据强凸函数的全局极小值点的唯一性和存在性定理,我们有:
(10)
另一方面〈BX,X〉是梯度L利普希茨连续的,我们有:
第二个不等式是因为次梯度不等式,第三个不等式是因为式(10),最后一个是因为函数〈BX,X〉的凸性。再将Yt的定义代入后得到

整理后得:
(11)
根据(11)可以得到序列

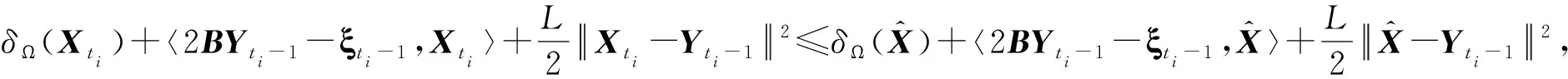
(12)
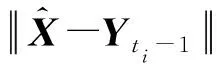


命题2(次线性收敛)设{Xt}为pDCA算法生成的序列,那么整个序列收敛的速度至少是次线性收敛的。
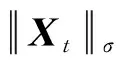
∂P(Xt+1)=2BXt+1-2CXt+1-ρΓt+1+NΩ(Xt+1),
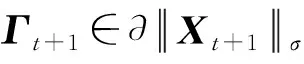
另一方面,从pDCA算法的最优性条件得出
0∈2BYt-2CXt-ρΓt+L(Xt+1-Yt)+NΩ(Xt+1),
因此存在Zt+1∈NΩ(Xt+1)使得
2BYt-2CXt-ρΓt+L(Xt+1-Yt)+Zt+1=0。
令

那么Wt+1∈∂P(Xt+1)且



4 数值实验
将本文提出的pDCA以及aDCA和对称移位高阶幂法(SS-HOPM)[14]以及DCA-APG进行比较,所有数值实验运行环境为Windows 11操作系统下的MATLAB R2015b。
采用的张量生成形式如下:

其中每个xi,yj∈Rn停止准则使用|P(Xt)-P(Xt+1)|≤10-8。每个算法均实验十次。
下表中Time表示所需时间;Fval表示十次实验中的最小值;Ave表示平均值;Max表示最大值;global表示所得到的解的最优性,数值越小越精确。

表1 当n=100时各个算法的情况
实验结果表明,pDCA和aDCA在计算时间和计算精度上相较于其他这两个算法都有很明显的优势,而aDCA在保留pDCA优势的基础上使得时间得到进一步的缩减。通过表2和表3我们可以看到,随着张量规模的增大,pDCA和aDCA的优势也得到了很好地保持,表明该算法有处理大规模问题的能力。

表2 当n=500时各个算法的情况

表3 当n=1000时各个算法的情况
4 结束语
对于球面约束下的四次型极小化问题,本文基于近端算法,提出了pDCA和aDCA,并证明了算法具有局部收敛性并且次线性收敛。该算法具有收敛速度快,计算精确度高的特点。本研究的不足之处在于未证明出该算法达到线性收敛,这也是我们接下去的研究目标。
