中心节点距离可控的加权树状网络一致性分析
2024-04-22李达权孙伟刚
李达权,孙伟刚
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
目前,作为多智能体系统中一种典型的集体行为,一致性问题因其在不同领域的广泛应用获得了越来越多的关注。在多智能体系统的一致性过程中,系统可能会受到外部干扰[1]。为了度量系统的抗干扰能力,文献[2]引入网络一致性的概念并证明了网络一致性完全由网络的拉普拉斯谱决定。由于拉普拉斯矩阵的特征值通常受网络拓扑结构决定[3],因此很难得到由所有非零特征值的倒数之和量化的网络一致性的精确结果。而对于若干类确定性网络,目前已经取得了很多解析结果,如文献[4]通过平均首次通达时间研究了加权Cayley网络一阶一致性,证明了网络一致性关于网络规模遵循四种类型的幂律;文献[5]探讨了多个领导者设置的领导-追随者网络一致性解析求解问题和领导者数目对网络一致性的影响;文献[6]研究了一类含有中心节点的单圈图的一致性,证明了中心节点的度差异越大一致性越好,但并未研究中心节点的距离和网络权重因子对网络一致性的影响。为此,构造一类具有可控中心节点距离的加权树状网络为研究对象,利用其规则的拓扑结构,得到网络一致性关于中心节点的距离和权重因子的解析表达式,探讨中心节点的距离和网络权重因子对网络一致性的影响。
1 预备知识
1.1 网络一致性的定义
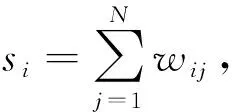
在一阶一致性问题中,在时间t处,每个节点i的状态用xi(t)来表示,整个系统在时间t的状态由向量x(t)∈RN给出。每个节点状态都会受到随机干扰,目标是让节点在其当前状态的平均值上保持一致。该系统的动力学方程如下:
(1)
式中,L是拉普拉斯矩阵,ω(t)是一个高斯白噪声随机过程且是一个N维零均值向量。在系统不存在噪声情况下,系统每个节点状态达到一致;在有噪声情况下,系统的各节点无法达到完全一致,而是在平均值处波动。为了测量这些波动的方差,引入网络一致性来量化这些波动的稳态方差,也是对含噪声鲁棒性的度量。
网络一致性定义为各个节点的状态偏离所有节点平均值的平均稳态方差,即
定义系统(1)的输出为
y(t)=Jx(t)
(2)

(3)
引理设p(x)=anxn+an-1xn-1+…+a2x2+a1x+a0是一个多项式函数,n≥2且a0≠0。则
(4)
式中,λi(i=1,2,3,…,n)表示方程p(x)=0的根[7]。
证明:
由于λi(i=1,2,3,…,n)为方程p(x)=0的n个根,

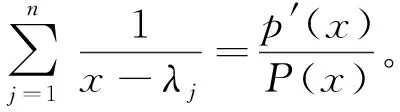
2 加权树状网络一致性的精确计算
2.1 加权树状网络
由于拉普拉斯矩阵的特征值通常受网络拓扑结构所决定,因此很难获得由所有非零特征值的倒数之和量化的网络一致性的精确结果。因此选取一类含有两个中心节点的加权树状网络,其距离用d来表示,中心节点的度由其所连接的节点数目m和n控制,网络规模为N=m+n+d+1。由于这类加权网络具有规则的拓扑结构,可以得到网络一致性关于中心节点距离和权重因子的解析解。图1给出了该网络模型的拓扑结构。
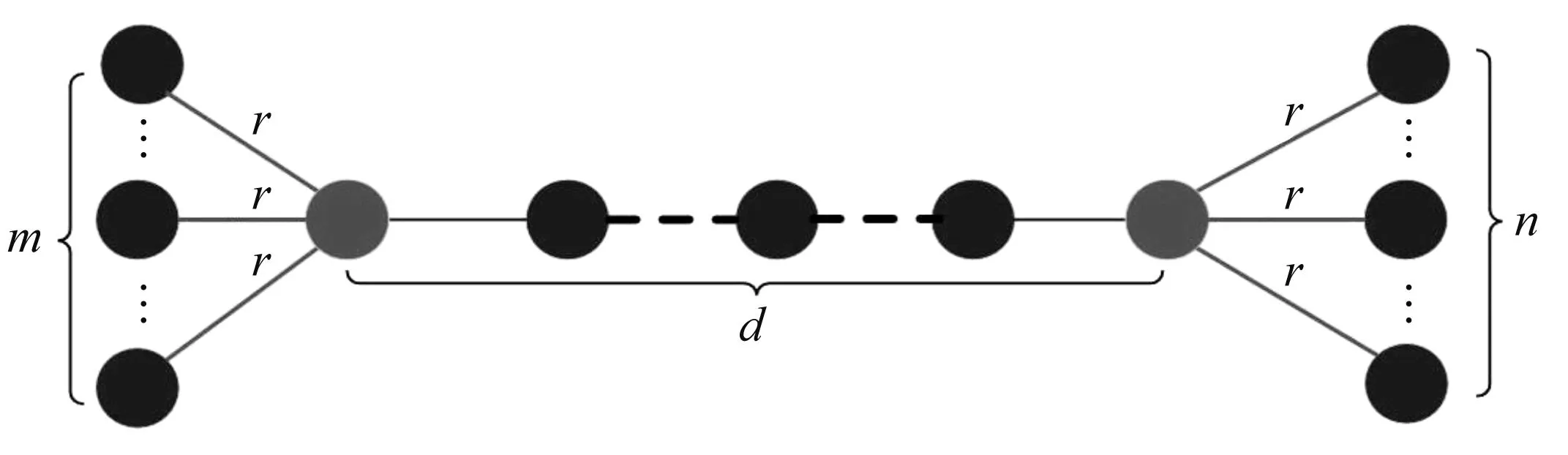
图1 一类加权树状网络,红色圆圈表示中心节点,红色实线表示加权
2.2 网络一致性的精确计算
定理网络一致性解析表达式为
从表3中数据可以看出,该支承辊试样化学成分中的碳含量较标准值稍低,虽然不符合JB/T4120—2006《大型锻造合金钢支承辊》标准中70Cr3Mo钢的成分要求,但碳含量基本接近标准的下限值,不是导致支承辊剥落掉块的主要原因。
证明:根据网络拓扑结构,其拉普拉斯矩阵L表示如下:
式中,I为一个m+n阶的单位矩阵以及
为了得到拉普拉斯矩阵L的特征多项式P(λ)的结果,经过行列式初等变换,得
(5)
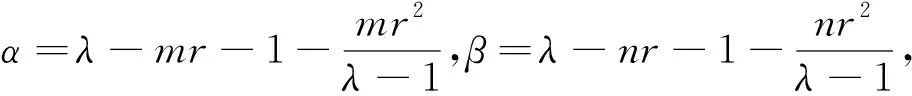
(6)
由式(6)可得如下递归关系:
Uk(λ)=(λ-2)Uk-1(λ)-Uk-2(λ),k≥3
(7)
式中,U1(λ)=λ-2,U2(λ)=λ2-4λ+3为初始条件。由式(7)得,
式中,Uk(0),Uk(1),Uk(2)分别为λ的常数项,一次项系数和二次项系数。
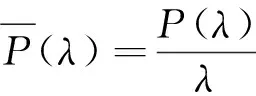
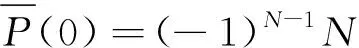
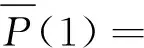
结合式(3)和式(4)网络一致性解析表达式为
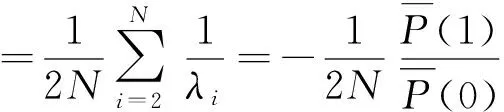
3 网络一致性的鲁棒性分析
根据网络一致性解析表达式H,通过Matlab数值模拟得到图2、图3和图4。研究分析了以下三方面内容:一、图2为权重因子r对网络一致性H的影响,发现当权重越大时,一致性越好;二、图3一致性H关于两个中心节点之间的距离d的关系,表明距离越短,一致性越好;三、图4为中心节点所连节点数目m对一致性H的作用,当固定一个中心节点所连节点数目时,则另一个中心节点所连节点数目越少,即初始节点数目越少,一致性越好。另外,固定网络规模N以及距离d和权重r不变时,可以得到中心节点的度相差越大,即|m-n|r越大时,网络一致性越好,对噪声更具鲁棒性。

图2 网络一致性H关于权重r的分布图
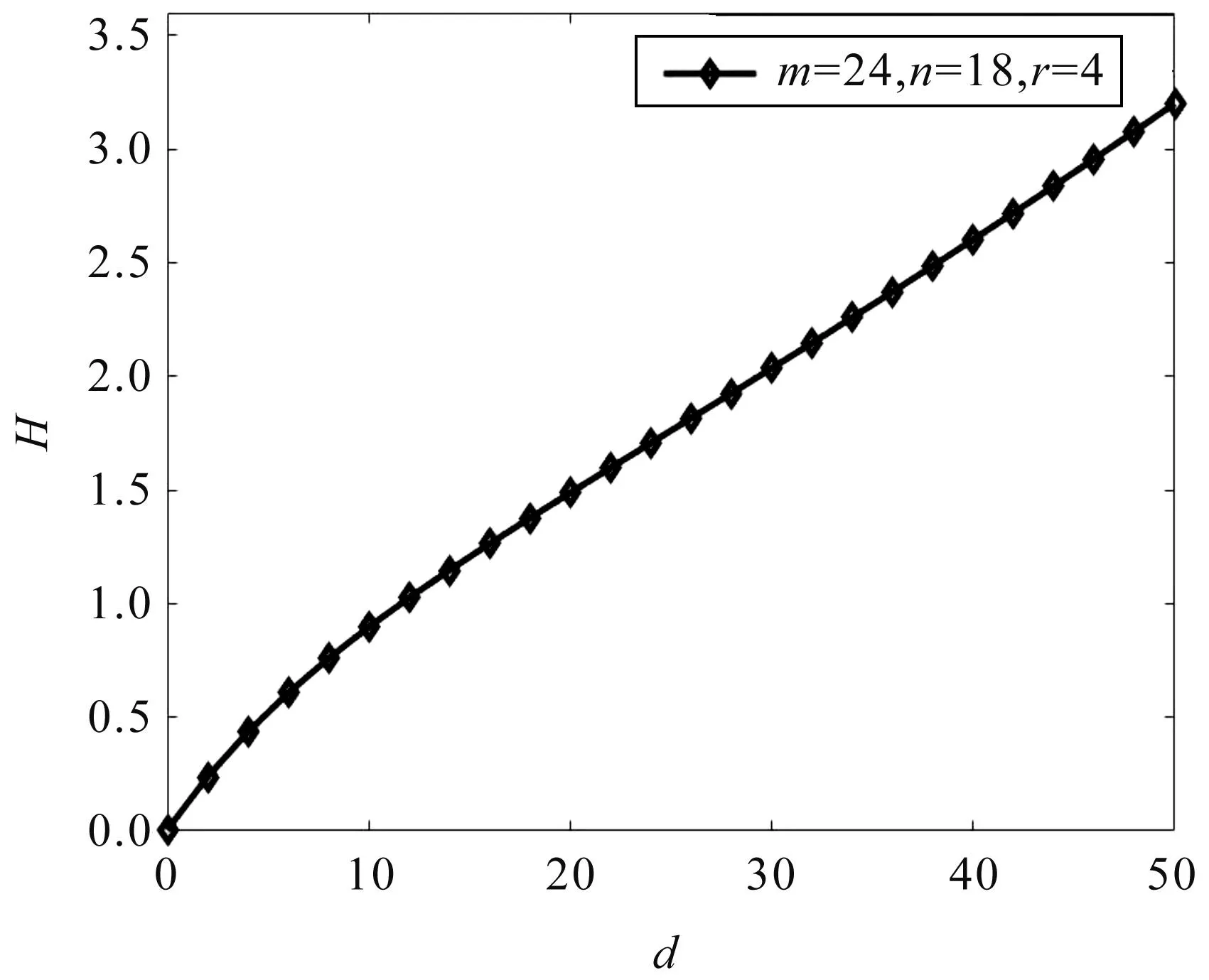
图3 网络一致性H关于两个中心节点之间的距离d的分布图
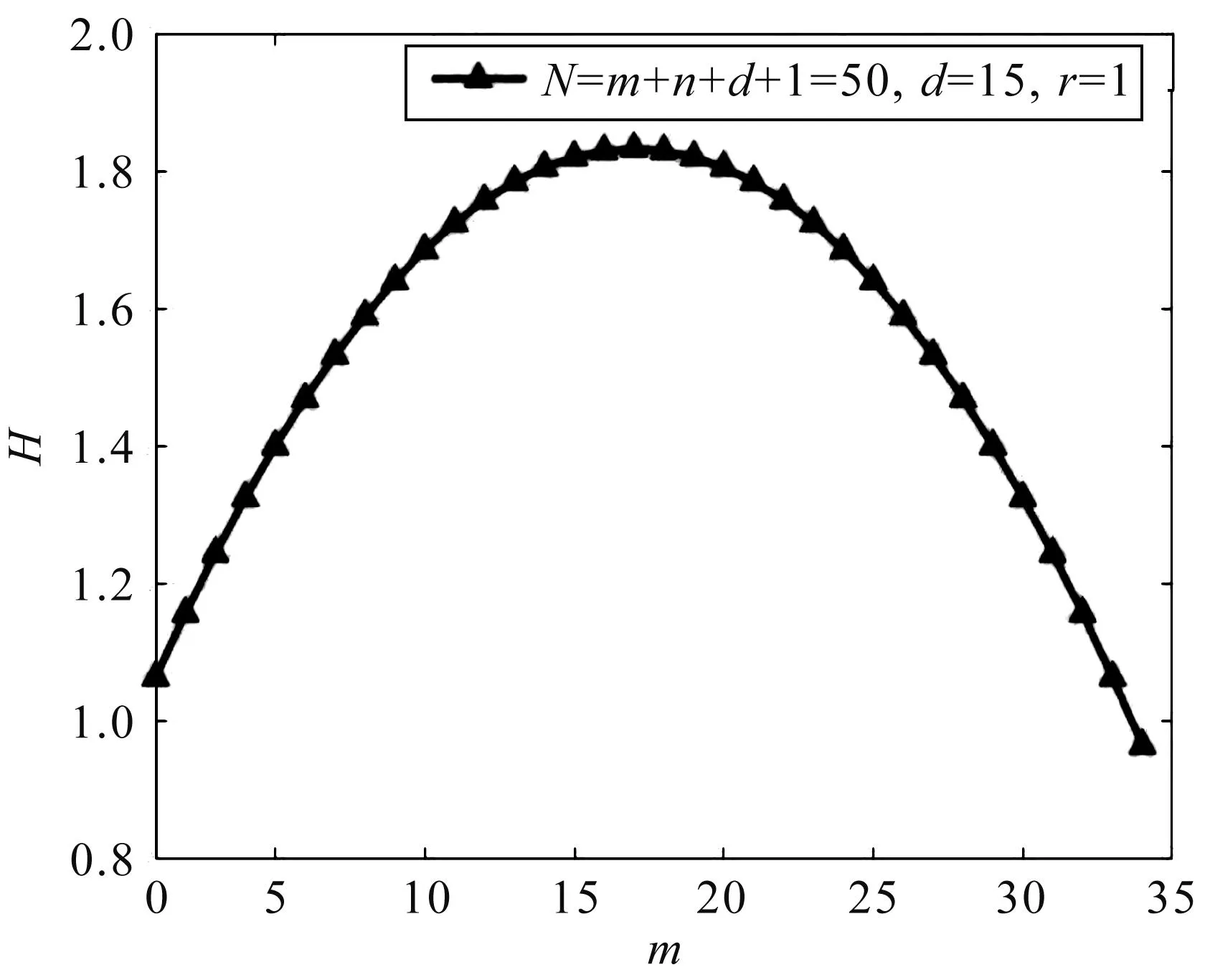
图4 网络一致性H关于中心节点所连节点数目m的分布图
4 结束语
选取一类加权树状网络为研究对象,研究了可控中心节点距离的加权树状网络一致性,通过计算得到了网络一致性的解析表达式并分析各网络参数分别对网络一致性的影响。由于拉普拉斯特征值与网络拓扑结构有关,权重因子在不同位置处及多个中心节点的网络一致性分析目前正在研究当中。
