Logistic混合模型的变分贝叶斯推断

龚 斌,赵 凝,郑 静

(杭州电子科技大学经济学院,浙江 杭州 310018)

0 引 言

然而,单一的概率模型无法满足实际的应用需求,于是有学者Pearson K[4]首次提出概率混合模型的概念。概率混合模型可以使用多个独立的概率分布去描述一个复杂的、使用单一概率模型无法描述,并且更符合现实中实际情况的数据分布。相比于单一的概率模型,混合模型具有诸多优点,因此若是能够将单一的Logistic回归模型推广到Logistic混合模型,不仅能够处理应对更复杂的数据集,同时也能扩大模型在一些热门领域的应用。

变分贝叶斯方法(Variational Bayesian Inference)[5][6][7]作为目前最有效的确定性近似方法,由于其计算成本小、收敛速度快、可用于大规模数据集处理而备受关注,常被用于解决概率混合模型的参数估计问题。郑丹阳等人[8]提出了一种基于变分推断的联合概率数据关联算法,用于解决关于雷达邻近多目标跟踪的问题,结果表明新算法具备更高的位置精度,且能有效地避免因邻近目标数量增多而引起的计算上的组合爆炸问题。刘连等人[9]针对传统的字典学习算法收敛速率慢、受到噪声干扰等问题提出一种基于变分推断的字典学习算法,显著提高了字典学习效率以及对测试图像的去噪效果和重构精度。

1 Logistic混合模型及其算法

1.1 Logistic混合模型

对于一组d维数据x=(x1,x2,…,xd)T,y∈{-1,1},假设w=(w1,…,wd)T为d维系数,则Logistic回归模型的密度函数p(y|x,w)可以表示为

p(y|x,w)=σ(ywTx)

(1)

接下来将其扩展至两分量Logistic混合模型。假设有N组d维数据,X={x1,x2,…,xN},xi∈Rd,i=1,2,…N,对应的应变量为Y={y1,y2,…,yN}。假设W={w1,w2}为系数参数,π={π1,π2}为权重参数,则两分量Logistic混合模型的密度函数为

(2)

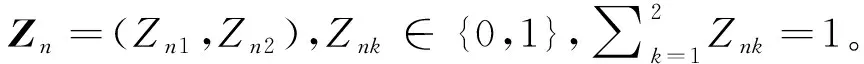
(3)

得到似然函数为

(4)

为方便起见,假设π={π1,π2}的先验分布是参数为α=(α0,α0)T的Dirichlet分布[10],即

(5)

同时假设wk服从协方差矩阵相同,均值不同的正态分布,即

(6)

两分量Logistic混合模型中各随机变量的关系如图一所示,其中随机变量用圆表示,变量之间的关系用有向箭头表示。综上(2)-(6)式,根据贝叶斯规则,可以得到观测值D和各个随机变量Θ={Z,W,π}之间的联合密度函数。

p(Z,W|D)∝p(Z,W,D)=p(Z,W,π,D)=p(D|Z,W)p(Z|π)p(π)p(W)

(7)

图1 两分量Logistic混合模型中各随机变量的关系示意图

1.2 变分贝叶斯推断

通常在使用概率混合模型解决实际问题时,还需要解决参数估计和模型选择这两个方面的问题。本文通过将模型分量数固定为两分量来解决模型选择的问题,后续将问题聚焦于如何解决两分量Logistic混合模型的参数估计上。而常用的混合模型往往会因为模型结构过于复杂而难以求解目标后验分布,因此通常使用变分贝叶斯推断方法来近似后验分布。

变分贝叶斯的主要思想是选择一族容易处理的分布族q(Θ)来近似真实的后验分布p(Θ|D)。首先假设变分分布族满足平均场理论,即

q(Θ)=q(Z,W,π)=q(Z)q(W)q(π)

(8)

又由贝叶斯定理得到

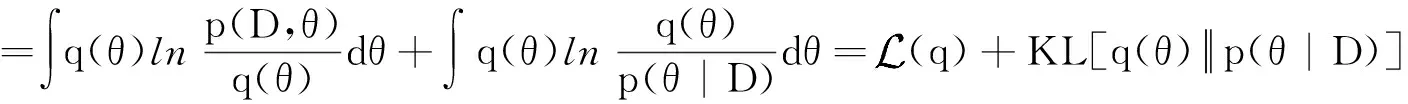
(9)

(10)

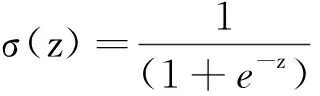
σ(z)≤exp[ξ*z-H(ξ)]

(11)

其中H(ξ)=-ξ*ln(ξ)-(1-ξ)*ln(1-ξ)

通过(11)将(10)中包含Logistic函数的部分转化为近似表示,即

(12)

(13)

1.2.1 q(Z)的变分推断

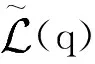
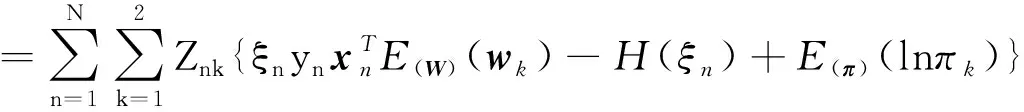
(14)

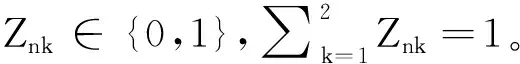
(15)

其中

(16)

且对于离散分布q(Z)而言,可以得到E(Z)(Znk)=rnk。

1.2.2q(π)的变分推断

(17)

因此

(18)

其中αN=(αN1,αN2)T

(19)

1.2.3 q(W)的变分推断

(20)

可得

其中Σk=I

(21)

进一步可得

(22)

根据上述推导得到的3个变分参数分布,进一步可得其中参数的期望:

E(W)(wk)=vk

(23)

E(π)(lnπk)=ψ(αNk)-ψ(αN1+αN2)

(24)

E(Z)(Znk)=rnk

(25)

其中ψ(·)为digamma函数。

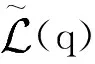
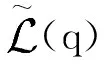
(26)

其中

(27)

(28)

(29)

(30)

(31)

(32)

整理得到

(33)

1.2.5 参数ξn的估计

通过将推导得到的(33)关于参数ξn求一阶导并令为0,得到ξn的参数估计,即

(34)

可得

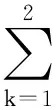
(35)

由于

(36)

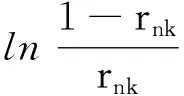
(37)

对等式(37)两边同时关于ξn求导得到r′nk:

(38)

其中

其中ψ′(·)为digamma函数的一阶导。

同样对等式(36)两边同时关于ξn求导得到ρ′nk:

(39)

综上根据(35)、(38)、(39),就得到了参数ξn的估计表达式:

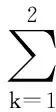
(40)

其中

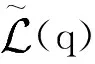
2 实证分析

为了验证本文提出的两分量Logistic混合模型变分贝叶斯算法的性能,通过将收集到的以下两组数据集按不同比例的混合来进行拟合检验。其中数据集1为Iris(鸢尾花)数据集,该数据集中每个样本有四个属性和一个类别标签,一共3个类别,为了更好地满足对上述模型算法的检验,选择其中两类作为第一组二分类数据集;数据集2为Banknote(纸币验证)数据集,该数据集也是一组每个样本拥有四个属性以及一个类别标签的二分类数据集。

实验中,将超参数进行如下初始化:α0初始化为1,μk为样本均值,wk用numpy库中的random函数进行随机初始化,权重系数πk都初始化为0.5。接下来将以上两组数据集按三种不同比例的混合,分别运用本文提出的变分贝叶斯算法来进行模拟验证。其中数据集A的混合比例为0.5,0.5;数据集B的混合比例为0.7,0.3;数据集C的混合比例为0.4,0.6。它们各自的变分下界变化趋势如下图所示。

图2 数据集A的变分下界趋势图

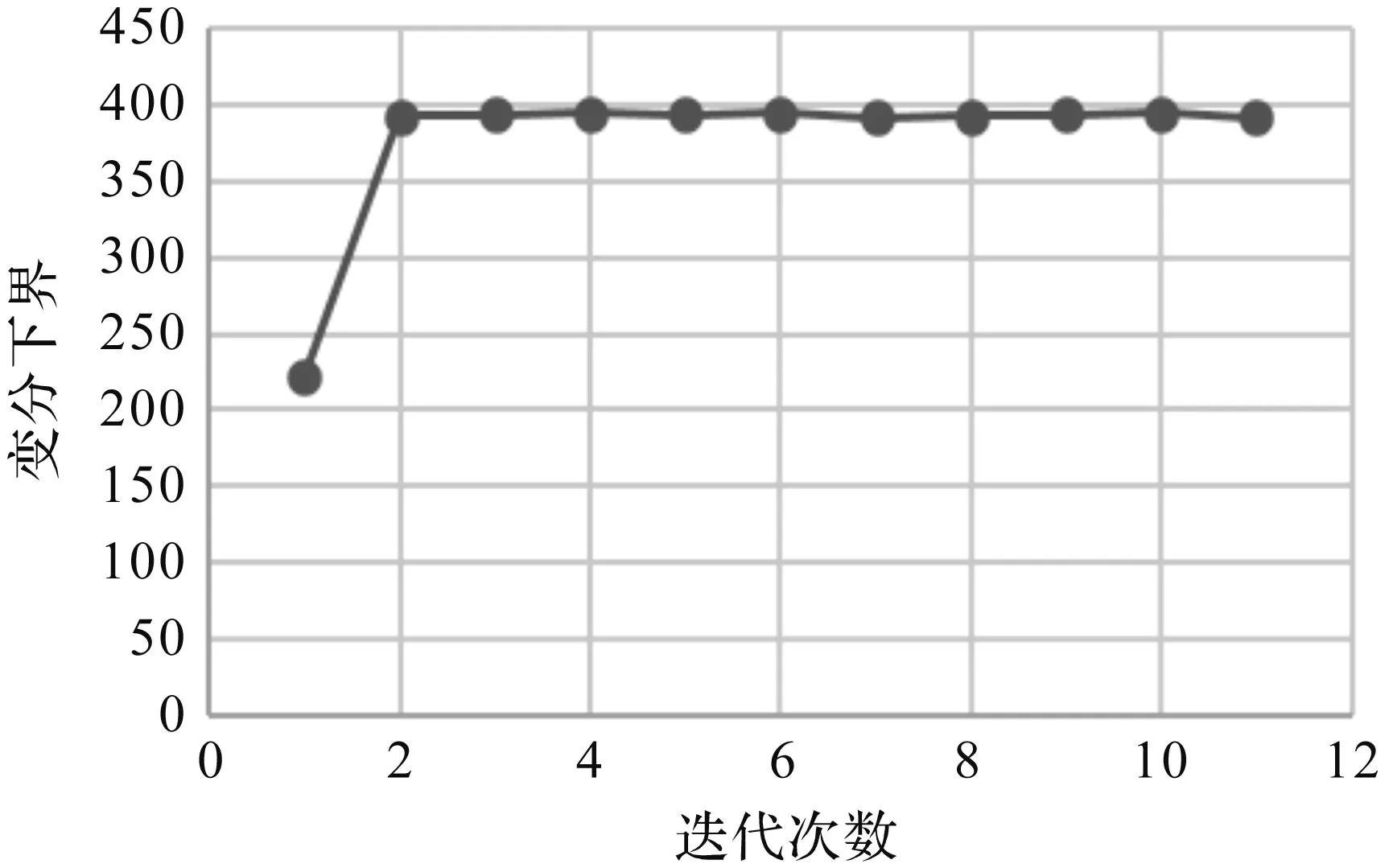
图3 数据集B的变分下界趋势图

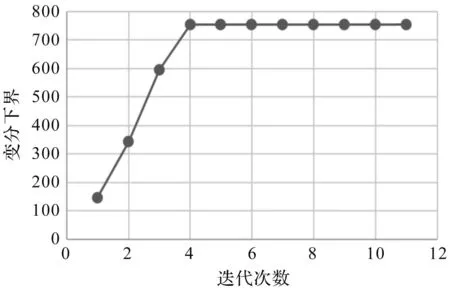
图4 数据集C的变分下界趋势图

从上述趋势图中可以发现,随着迭代次数的增加,变分下界很快就开始收敛,之后逐渐趋于平稳。

将变分下界进入收敛后的各个超参数以及参数的估计值结果整理如下表:

表1 三组混合数据集模型拟合结果

从表一的拟合结果来看,该算法在变分下界收敛达到平稳后得到的权重系数估计值跟实际的混合比例非常接近,说明该模型算法能在快速收敛的同时实现较为精确的混合分类数据集的混合比例估计。

3 结束语

传统的变分贝叶斯推断在处理混合模型的参数估计时,通常需要依赖平均场理论以及分布之间的共轭关系,对于无共轭分布的混合模型便无法进行有效的参数估计。本文通过将Logistic混合模型与变分贝叶斯推断法结合在一起,并借助Logistic函数的近似表示来解决不构成共轭分布的问题,提出一种能用于解决Logistic混合模型参数估计的贝叶斯推断算法,并给出了详细的变分推导过程。实证结果表明,该算法能够在保证精确估计混合比例的同时,实现快速收敛的效果。后续将针对如何实现拓展至多分类混合模型的变分贝叶斯推断进行深入研究。