有趣的“红包”问题

文／江苏省南通市通州区文山初级中学 吴佳豪

葛老师近期提供了一道思考题：过年了，小明面前有三个红包，并且其中一个红包有钱，另外两个红包是空的（具体哪个不知道）。小明随机挑选了一个红包没有打开，同时剩下的两个红包自动去掉一个没有钱的，这时小明有一次交换剩下红包的机会。请问小明应不应该选择交换并说明理由。

刚开始看到这道题的时候，我想：题目是不是出错了？换不换不都一样吗？这题有什么意思？

由于这道题要求说明理由，而且刚刚的想法也没有进行严谨的证明，于是我继续思考。因为小明最开始从三个红包中随机挑选到有钱和没钱的红包的可能性是不一样的，既然如此，后面的是否交换红包从逻辑上看，应该也会受到最初是否选到有钱的红包这个随机事件的影响。那么，好像换与不换是不一样的啊。

我想到的第一个解决方案是用频率估计概率。我进行的试验记录结果如下：

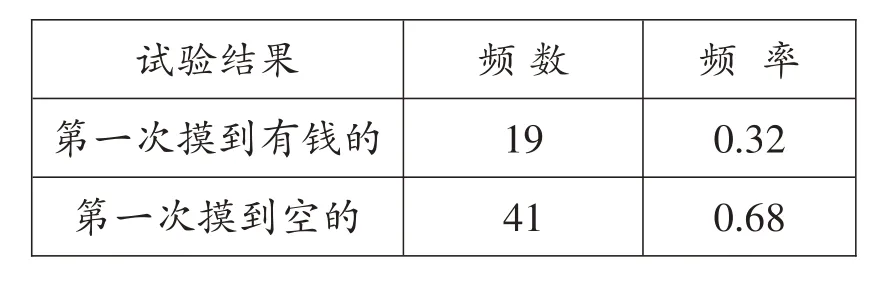
当第一次摸到有钱的红包的时候，剩下的两个红包都是空的，所以此时交换是亏的；当第一次摸到空的红包的时候，剩下的两个红包一个是空的，一个是有钱的，由于会自动去掉没有钱的红包，所以此时交换是赚的。根据表格中的数据，小明应该选择交换。

在用这个方法得出结果后，我进行了反思：用频率估计概率的方法虽然可行，但是试验的次数要足够多，有些耗时费力。有没有简便一点的方法呢？

我想到的第二种解决方法是分类讨论。我首先分别用空包1和空包2 来表示两个空的红包，那么以下3种情形都具有相等的可能性：

情形1：假设摸到的红包是有钱的，交换红包不划算；

情形2：假设摸到的是空包1，交换红包是划算的；

情形3：假设摸到的是空包2，交换红包是划算的。

综上，共有3 种等可能情形，3 次中有两次交换是划算的，所以小明应该选择交换。

通过思考，我得到了与直觉不同的答案。数学是一门极其严谨的学科，在思考问题时，我们应该多从逻辑层面去分析思考，通过严格的证明来得到正确的答案。

教师点评

小吴同学对一道“红包”问题进行了深入思考，从直觉感知到数学建模，从而推理出正确的结果，感悟到数学的魅力。事实上，很多数学真理的发现，都有这样的特点，往往会经历“直觉感知→数学抽象→数学建构→推理证明→确认性质→数学运用”的过程。同学们在今后的数学学习中，可以细细体会。