基于互相关的小型化低功耗超声波风速风向仪设计

郑健 卢会国,3*

(1 成都信息工程大学电子工程学院,成都 610225; 2 中国气象局大气探测重点开放实验室,成都 610225; 3 成都平原城市气象与环境四川省野外科学观测研究站,成都 610225)

引言

风由空气的运动产生,气象上通常将空气的水平运动称作风,空气在运动过程中会造成空间中热量和水汽的交换,这个过程会伴随着天气的变化,标志着某种天气过程的发生和演变[1]。风不仅对天气以及大气中的水汽分布产生影响,产生旱涝灾害[2],也对自然地貌的短期或长期的演变起到推动作用[3],影响农业生产与防灾减灾[4-5]。

现阶段风的测量多采用机械式风杯和翼型风向标,测风塔进行风速风向测量[6],除此之外也有超声波风速风向仪实现对风的测量。超声波测风相比于传统的风杯或者翼型风标,具有无机械结构,耐磨损和启动风速小的特点,其基本原理主要利用两组探头分别在x和y方向测量对应的风速分量,再根据矢量合成得到最终的风速值[7]。利用这种方法测量得到的风速精度在0.1 m/s,风向精度在1°以内[8]。除了二维测风方法外,还以通过多组超声波探头组成三维结构进行三维风测量[9],或者组成阵元结构增强对噪声的抑制能力提高风速测量精度[10-11]。

对于特殊工作环境下超声波风速风向仪一般自带加热功能,在探头结冰时内部电路提供加热使其能在极端严寒的条件下工作,外观上一般呈现“十”字对发对收结构,这种类型的超声波风速风向仪探头之间距离一般为200 mm,具有较大的体积(尺寸为424 mm×287 mm),这样的设备仅有一些特殊的大风洞或者对风洞工作段进行整改方能进行测量[12]。目前省级风洞都不具备测量和检定能力[13](省级风洞观测实验窗仅为80 mm,远远小于常规风洞1m×1m试验窗[14]),功耗较大,一般在8 W左右,带加热超过70 W,数据采集处理一般使用DSP(Digital Signal Processor)或者单片机完成[15]。FPGA(Field Programmable Gate Array)相比DSP,在高速率信号处理方面具有明显优势[16],特别适用于数据量大,实时性高的场合,且超声波风速风向仪的核心是测量超声波信号到达的时间,具有算法处理较为简单,但对实时性要求较高的特点,因此使用FPGA处理相比于DSP更具有优势。

国产FPGA目前正处于高速发展的时期,特别是低功耗FPGA,较突出的有安路科技(Anlogic) EF2系列FPGA[17],工作频率400 MHz下功耗仅为0.053 W,可结合FIR(Finite Impulse Respond)滤波器和互相关波形检测算法逻辑,能明显提高超声波风速风向仪的稳定性和精度,并达到超声波风速风向仪核心器件国产化的目的。

采用FPGA作为主控的风速风向仪,主要利用倾斜45°的探头向挡板发射超声波脉冲,超声波脉冲由挡板反射后被另外一只探头接收完成一次测量[18]。这种结构设计使得探头之间的距离缩小到80 mm,明显缩小了超声波风速风向仪的体积,使得超声波风速风向仪在省级风洞均可计量检定。

1 反射式超声波风速风向仪测量原理

超声波风速风向仪基本测量原理有时差法,相差法和多普勒频移法三种,使用较多的是时差法和相差法,相差法易出现相位模糊且风速测量范围较短,相比于时差法较少使用[19]。

与直接式二维超声波风速风向仪类似,反射式超声波风速风向仪同样有x和y两个方向,并且相互垂直,如图1所示为反射式超声波风速风向仪x方向上剖面图,探头A和B与挡板之间相互倾斜,倾角为α,两个探头之间的距离为a,上下挡板之间的高度为d。探头A发射超声波脉冲信号经过路径传播到上挡板被反射,最后被探头B接收[20-21]。

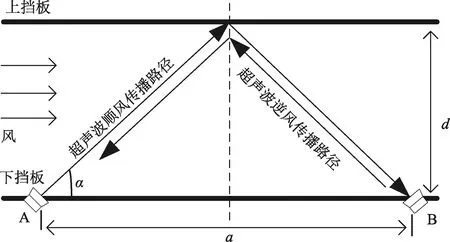
图1 超声波传播路径剖面

在实际过程中超声波探头与挡板之间的倾角α为

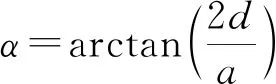
(1)

式(1)中,d上下挡板间距,a两个探头之间的距离。

当顺风的时候超声波的传播时间t1为

(2)

逆风时超声波的传播时间t2为

(3)

式(2)和(3)中,c为声速,v为风速。

根据式(2),(3)可得到在此x方向上的风速值vx和声音的传播速度c

(4)

(5)

按照同样的原理,在垂直探头A、探头B的位置,按照同样的方式放置探头C、探头D,测量超声波在探头C、探头D之间顺风传播的时间差t3,逆风传播的时间差t4,可以得到在该y方向上的风速vy为

(6)

式中,α与式(2),(3),(4),(5)中的夹角为同一个值,t3为y方向上的顺风时差,t4为逆风时差。探头整体布局如图2所示,vx和vy分别为真实风速v在x和y方向上的分量,通过对vx和vy进行矢量合成可得到真实风速v[22-23]。

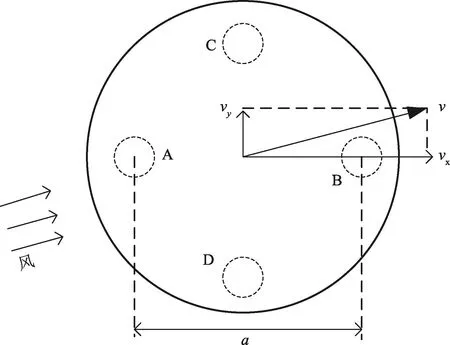
图2 二维超声波风速风向测量具体原理

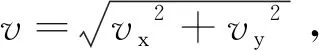
(7)

2 超声波硬件设计

反射式小型化超声波风速风向仪的硬件组成主要包括FPGA控制电路,超声波探头驱动电路,超声波接收电路,模拟开关和高速ADC。FPGA控制电路主要完成整个系统的逻辑控制和测量超声波在顺风和逆风的时差。具体控制逻辑如图3所示,四只探头会依次接收到FPGA的控制信号,并工作在脉冲产生或者接收超声波脉冲的过程中,接收到的超声波脉冲信号先经过ADC(Analog Digital Converter)量化,再由FPGA处理得到波形到达的准确时间,最后通过计算即可得到具体风速值。

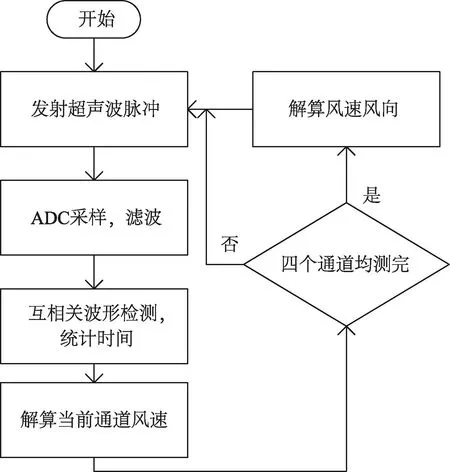
图3 超声波风速风向仪具体控制流程

为了能够有效提高风向测量精度,小型化超声波风速风向仪所选用的探头具有较窄的波束宽度,半功率角为10°,但过窄的波束宽度会降低风速测量范围,探头的正常工作驱动电压应在60 V以上,最高驱动电压不超过400 V,因此需要对驱动脉冲进行升压处理,驱动电路如图4所示。利用PMOS管和变压器可将FPGA产生的200 kHz脉冲信号升压到60 V以上的脉冲电压并驱动超声波探头正常工作,每次驱动的时候仅需要3个脉冲即可,整个测量周期内只需要12个脉冲,这种驱动方式可节约绝大多数的能量,降低了超声波风速风向仪的功耗。

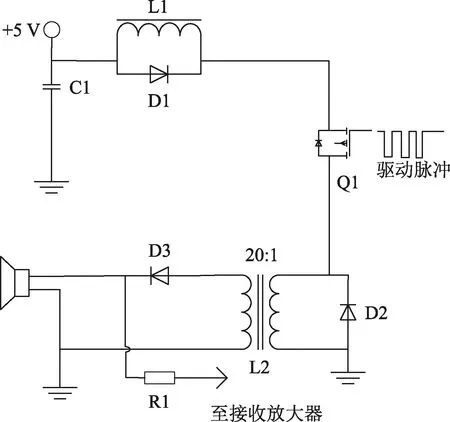
图4 超声波探头升压驱动电路

如图4所示,发射脉冲引脚默认状态下为高电平,当变为低电平时,Q1场效应管的栅极变为低电平,场效应管开启,此时5 V电压通过二级管D1到场效应管Q1加到变压器L2上面,经过变压器将交变的脉冲电压升压到60 V以上,FPGA驱动波形和变压器升压输出波形如图5所示。

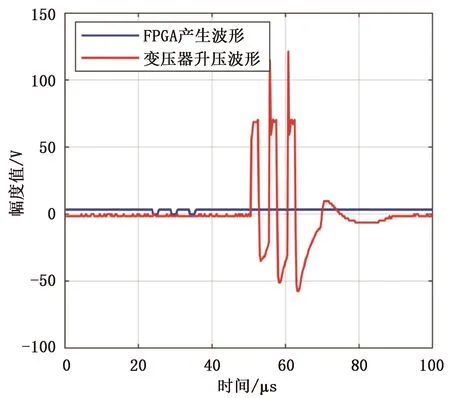
图5 FPGA直接输出波形与经过变压器升压后的波形对比

当Q1断开以后,变压器两端电流不能突变,于是会在变压器两端产生瞬态高压,这部分瞬态高压通过图4中二级管D2释放,还有一部分瞬态高压经过Q1的体二极管被电感L1吸收。其中电阻R1用作超声波探头的阻抗匹配与信号接收回路。

当图4中的脉冲信号置高电平时,场效应管Q1处于高阻状态,此时探头转换为接收状态,超声波探头接收到的微弱信号经过图6中电阻R1之后至Q2和Q3两个NPN三极管组成放大电路中进行放大,其中C2和R6组成一个简单的抗混叠滤波器,C3主要作用为减弱通道切换的时候直流电平的影响。

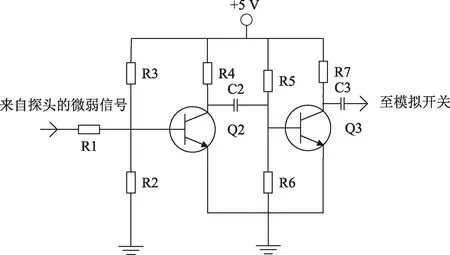
图6 超声波接收前级电路

通道切换使用RS2255四选一模拟开关完成,再经由12位模数转换器AD9226将模拟信号转化为数字信号到FPGA中做进一步处理。

3 软件算法设计

3.1 FIR带通滤波器设计

FIR滤波器是一种非递归型的滤波器,相比于IIR(Infinite Impulse Response)滤波器具有线性相位和稳定性高的优点,但也具有达到相同的水平衰减程度,FIR滤波器所需要的阶数要远远多于IIR滤波器的缺点。超声波探头所接收到的波形类似于单脉冲调幅的波形,有明显的起振和衰减过程,频率为200 kHz,含有多种频率成分,如图7所示,因此不能使用IIR滤波器,需要设计FIR滤波器滤除信号中的噪声,较为简单的思路是采用Matlab中Fdatool工具进行设计,最后导出滤波参数即可。

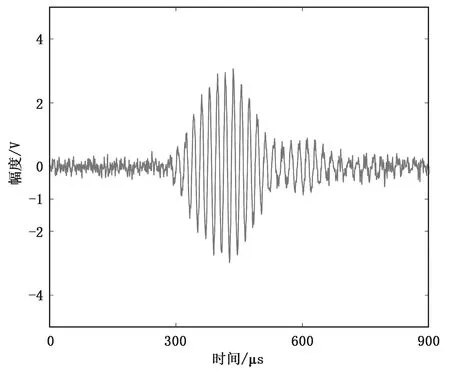
图7 超声波探头接收波形

FIR滤波器的单位抽样响应h(n)是一个有限长序列,对应的系统函数可以表示为

(8)

式中,h(n)为滤波器的单位抽样序列,长度为N,且为偶数,z为复数域参数,通过拉普拉斯变换得到。FIR滤波器系数序列h(n)是具有线性相位对称性的,可以分为偶对称的FIR滤波器和奇对称的FIR滤波器。在小型化超声波风速风向仪设计中,设计的滤波器为中心频率f0=200 kHz的带通滤波器,滤波器阶数N为偶数,滤波器采样率Fs与ADC采样率一致,在FPGA中滤波的过程实际为流水线进行,当有新的采样数据进来之后,滤波值也会随之输出,为了节约乘法器资源根据FIR滤波器的对称性只需要使用一半的滤波器系数,因此实际使用的滤波器系数为b(n)

(9)

式中,b(n)为实际滤波器序列,长度为h(n)的一半,将采样序列x(n)与h(n)对齐部分进行折叠,由于b(n)只有h(n)的一半,因此x(n)在折叠之后还需要对应相加,再与b(n)进行乘累加运算,最终得到输出序列y(k)

(10)

式中,k为整数,取值范围为0～M-1,M为采样序列的长度,在计算过程中超过x(n)长度部分自动补零,y(k)为滤波器的输出结果。

3.2 互相关波形到达时间检测

超声波风速风向仪的核心是计算波形到达时间,常用的方法有幅度值检测法和失配滤波法,幅度值检测法主要通过设置幅度值阈值来判断波形到达时间[24],但这种方法受噪声影响较大,在低信噪比信号的环境下波形到达时间计算具有很大的误差,失配滤波法主要通过对频域加窗达到时域波形压缩的目的,相比于互相关检测法,失配滤波器法计算量较大,在FPGA中需要消耗较多的资源[25-26]。

波形到达时间测量在某种程度上可以通过比对滤波器输出序列与参考序列的相似程度作为依据,判断波形是否到达。相似程度通常使用互相关进行描述。对于式(10)滤波器输出序列y(k)与参考序列y′(k)而言,相关系数ρ定义为

(11)

式中,滤波器输出序列y(k)长度为M,参考序列y′(k)长度M′,由于ρ分母的值为各自能量乘积的开方,具体的开方值是一个常数,因此相关系数ρ大小可以由分子rxx′确定

(12)

式中,rxx′描述了两个信号的相似程度,在实际过程中两个序列长度并不相等,参考序列y′(k)为系统存储的超声波预接收序列,长度M′是固定值,滤波器输出序列y(k)长度M是未知的,通常M远大于M′,可以视为参考信号y′(k)在滤波器输出序列y(k)上滑动,此外滤波器输出序列y(k)和参考序列y′(k)之间的采样率应该保持一致,两个信号之间的互相关定义为R(k)

(13)

式中,k为整数,取值范围为0～M-1,实际过程中为了提高互相关运算后对超声波信号的检测能力,减少波动程度,可以对R(k)取绝对值,最终判断到达时间的信号为R′(k)

(14)

式中,R(k)为原始互相关计算结果,R′(k)为R(k)绝对值,互相关各阶段处理结果如图8所示。

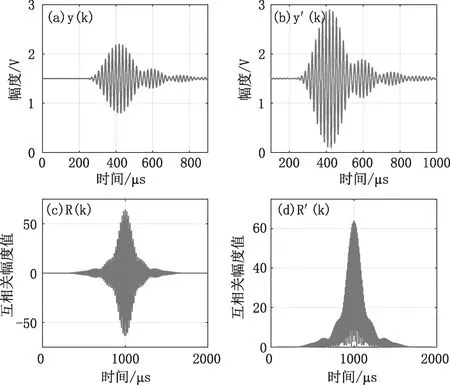
图8 互相关检测算法各阶段结果:(a) FIR滤波器输出序列,(b) 参考序列,(c) 互相关运算输出结果,(d) 互相关输出结果绝对值

如果要进一步降低互相关测量到达时间过程中的波动程度,可以再使用一个截至频率f2=400 kHz以下的低通滤波器提取互相关输出结果绝对值的包络,再计算包络的峰值,这样可以使测量得到的时间差波动程度更小。

4 系统测试

超声波风速风向仪的电路和PCB使用Candence Allegro软件设计完成,并制作外壳,安装超声波传感器,焊接电路板制作成品。为了能够提高风速风向仪的防水性能,还需要使用航空插头和线缆作为外部连接。整机测试使用UTP3303电源进行供电,调整输出电压为12 V,连接小型化超声波风速风向仪,使用万用表测量供电电流为24 mA,连续多次测量并绘制电流随测量次数变化曲线如图9所示。

图9 风速风向仪功耗实测值及曲线

图10为使用型号为HDF-720低速回路风洞对风速风向仪进行实测,HDF-720风洞可提供风速范围为0.05～61.5 m/s,可控制风洞产生不同风速段的水平风来模拟自然风,同时由于风洞处于实验室教学区附近,考虑安全以及不干扰他人正常学习的因素,对超声波风速风向仪进行检定的风速范围为0～40 m/s,并固定风速风向仪于中速风段内。

图10 风洞检定实测

测试过程中以0°方向将风速风向仪朝向来风,同时调整风洞的风速分别在0 m/s,5 m/s,10 m/s,20 m/s,30 m/s,40 m/s测得数据,以及在风速测量基本稳定情况下旋转风速风向仪一周测得风速与风向数据,将固定风向测得风速值测得数据绘制风速变化直方图如图11所示,并统计单风速点样本长度为L的方差。

(15)

图11 固定方位角下不同风洞风速段实测数据分布直方图:(a) 0 m/s, (b) 5 m/s, (c) 10 m/s, (d) 20 m/s, (e) 30 m/s, (f) 40 m/s

通过图11可以发现使用互相关法设计的超声波风速风向仪在30 m/s以下时有较好的准确性和较高的稳定性,在30 m/s以下时,风速风向仪输出数据基本与风洞值基本一致,在20 m/s以下时数据较为集中,基本符合正态分布,在30 m/s以上是数据开始分散,且与正态分布相符度较差。这主要是由于在无风或低风速时候超声波信号受风速影响较小,信号衰减程度较低,有较为良好的信号质量,使用互相关计算超声波信号到达时间准确度优于强风情况,因此低风速时风速风向仪测量精度较高,随着风速的增加,超声波信号质量逐渐降低,测量误差逐渐增大,精度降低。

为了进一步评判基于互相关的低功耗小型化超声波风速风向仪测风的准确性,使用了绝对误差(表1),绝对误差Δ定义为

表1 超声风实测值与标准器对比

Δ=s0-s

(16)

其中,s0为标准器风速值,s为超声波风速风向仪实测值。

表1的数据对比表明,0～5 m/s最大测量误差在±0.3 m/s,5～20 m/s最大测量误差在±0.5 m/s,由于超声波信号的衰减,在40 m/s时风速风向仪有较大的测量误差。除此以外在测量过程中仪器晃动的影响,较大风时阴影效应的存在也会对大风的测量造成影响。

在风速稳定后从0°～360°朝向风洞来风方向旋转超声波风速风向仪测得不同方位角下对应风速值,按照方位角与风速值的关系绘制极坐标图。

图12中不同风速段对应不同方位角实测风速值在极坐标中并不是一个标准的圆形,主要由于图9结构影响,风在经过图9结构的支撑柱时会形成湍流以及阻碍,造成风速测量结果会有较大的波动,同时也由于探头的阻碍会形成一定的阴影效应使得从90°,180°,270°和360°方向风速值偏小。也由于风速值增加造成传感器本身的一些倾斜导致并不是完全垂直于风的来向,造成在20～30 m/s强风时不同方位角风速值发生较大波动,而在40 m/s时由于超声波信号衰减造成风速值波动的影响要远大于结构以及阴影效应的影响,是风速在40 m/s以上测量误差较大的主要原因。

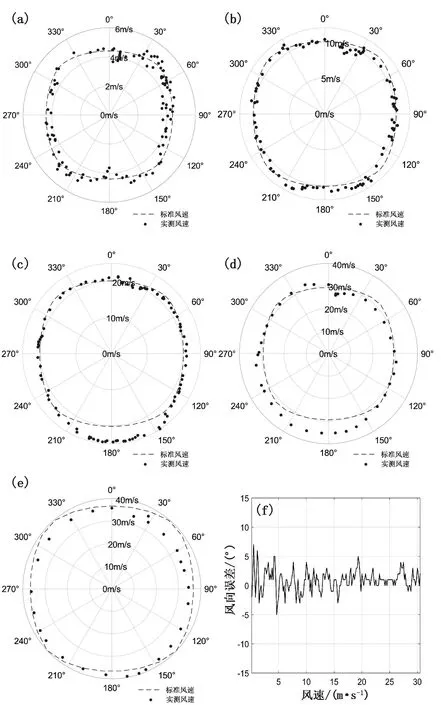
图12 0°～360°方位角下风洞风速为5 m/s (a), 10 m/s (b), 20 m/s (c), 30 m/s (d),40 m/s (e)风速实测值与360°方位角下风向误差(f)

在图12中同时测试了在0～30 m/s变化风速下固定方位角朝向北风时的风向变化情况,从试验数据图中发现风速稳定时候风向几乎没有变化,风向测量最大误差在±1°以内,而在风洞风速跳变时风向值会发生剧烈抖动,最大测量误差降低到±5°以内,这是主要由于风速跳变过程中风速值本身的不稳定造成了风向的波动。

5 结论

通过风洞试验发现,采用国产FPGA结合互相关波形到达时间检测原理设计的风速风向仪在实际风洞测试中具有较高的测量精度,当风洞风速平稳时,实测风速精度能达到风速测量±0.5 m/s,实测风向精度能达到±1°,风速测量范围在0～35 m/s风速段内最大风速测量误差优于±5%。在使用外置电源供电的情况下整机功耗约0.2 W,体积小巧(包含外壳长110 mm,宽110 mm,高120 mm)。相比于传统的幅度值检测法或者起始波形检测法,互相关计算方法无论是风速测量还是风向测量以及抗噪声性能方面都有很大的优势,采用FPGA的设计方法使得风速风向仪能够在复杂环境以及其他多种干扰环境下正常工作,提高了风速风向测量次数,达到每秒钟50次。整体设计缩小了尺寸,降低了成本和功耗,使超声波风速风向仪可以被大面积推广和应用。