基于年际增量法的广西6月月降水量预测
2024-04-19蔡悦幸史旭明陆虹金龙罗小莉
蔡悦幸 史旭明 陆虹 金龙 罗小莉
(1 广西壮族自治区气候中心,南宁 530022; 2 桂林航天工业学院,桂林 541004)
引言
广西地处亚热带季风气候区,南濒热带海洋,受低纬热带天气系统和中高纬大尺度环流系统的交替影响,降雨时空分布严重不均,尤其是6月,作为气候平均月降水量最多的月份[1],常因强降雨的集中发生,导致河水暴涨、洪水泛滥、城市内涝、滑坡泥石流等,造成巨大的经济损失,甚至危及人民生命。因此,深入研究影响广西6月降水的大气环流演变规律,分析其影响机制和主要影响因子,建立气候预测模型,提高6月降水预测的准确率,为政府和各级部门防御洪涝灾害减少经济损失提供科学决策支撑,具有重要意义。
与短期降水天气预报相比,影响月时间尺度降水变化的因素更多、更为复杂,要提高月降水趋势预测准确率更为困难。近年来,许多学者为提高短期气候预测准确率提出了基于不同原理的动力统计相结合的预报方法,如回溯差分格式预报方法[2-4]、动力-统计相似误差订正预报方法[5-10]、组合统计降尺度预测方法[11-14]等,均取得了较好的预测效果[15-17]。然而气候模式对同期大尺度环流的有限可预报性,会在一定程度上影响统计降尺度模型的预测性能[12]。王会军等[16]也指出气候模式所预测的各因素间可能存在着复杂的关联,任何动力-统计预测模式都不可能把所有因素考虑吸纳,并提出了学者们需要创新研究动力-统计相结合的预测模型。据此,有不少学者利用人工智能方法结合统计预测方法,提出了基于不同机器学习方法的天气气候预测模型,在一定程度上提高了预测准确率[18-24]。因此,利用机器学习方法预测月降水量,有助于为短期气候预测提供一种可能的参考。
目前已有大量研究发现,广西前汛期降水与前期欧亚中高纬度地区环流形势[25-27]、高原积雪[28]、各区域海温[29-30]以及南半球环流[26-27,31]等有密切联系。以上系统的异常,会引起大气环流形势的异常配置[32-33],进而造成了天气气候的异常[34]。由于各不同因子间的不确定性和复杂的相互作用过程,以及降水的年际、年代际预测信号的不一致均容易导致预测模型误差增大[35],很多学者利用年际增量法来放大预测因子与预测对象之间的异常信号,同时减小气候年际、年代际背景带来的影响[36],并采用多元线性回归预报方法来建立预测模型,均取得了良好的预测效果[35-40]。然而,多元回归预报方法容易出现自变量间的多重相关性,从而影响回归模型的参数估计,扩大模型预测误差[41-45];另一方面,强降水事件受多尺度天气系统综合影响,具有显著的非线性特征,因此,应用非线性方法来进行建模更有利于减少模型误差。近年来,模糊神经网络方法由于具有较强的处理非线性问题能力,在气象预报领域得到了广泛应用[18-20]。也有研究表明熵度量是信息量大小的度量[46-47],可以用来衡量集成个体模型对预测模型的影响。因此,本文尝试采用模糊神经网络方法与熵度量方法,利用广西87个站6月平均月降水量的年际增量序列作为预报量,通过普查1960—2021年6月降水年际增量与前期500 hPa位势高度场的相关性,选取影响广西6月降水异常相关性较高的前期预测因子,构建月降水年际增量的集合预报模型,探索这种集合预报模型的预报效果,验证其在短期气候预测中的有效性和适用性。
1 资料和方法
1.1 资料
降水资料为广西87个国家气象观测站1959—2021年6月降水观测数据;大气环流资料为美国国家环境预报中心和大气研究中心(NCEP/NCAR)再分析数据[48],包括逐月位势高度场、风场,水平分辨率为2.5°×2.5°。
1.2 方法
本文参照范可等[35]定义的年际增量法,通过预测广西6月降水年际增量(即当年6月降水量减去上一年6月降水量的差值)来预测广西6月的降水量。分析NCEP/NCAR大气环流再分析资料中逐月位势高度场、风场,挑选物理意义明确、相关系数高的主要影响因子,利用模糊神经网络方法[49]、熵度量方法[50]来建立广西6月降水年际增量的预报模型。
2 预测因子的选取及机制分析
本文在预选因子群中挑选预测因子时,不仅考虑因子与预报量序列相关系数的大小以及预选因子间的相关性,还根据近年来对广西6月降水机制的相关研究成果[1,26-31,51-54],挑选与广西6月降水有关的、物理意义较明确且因子间相关关系相对独立的因子。
2.1 预选因子群的建立
以500 hPa位势高度场再分析资料作为基本预报因子场,计算6月降水量原始序列、增量序列分别与前期上年1月至当年4月逐月、连续2月滑动平均、连续3月滑动平均以及连续4月滑动平均的500 hPa位势高度原始场及增量场的相关关系,挑选连续20个格点以上相关系数|r|≥0.25的区域作为一个因子区,再对因子区内最大值附近的9个格点值进行逐年平均,该序列作为代表该区域一个预选因子。陆虹等[20]研究发现,选因子时,将2个相邻区域且符号相反的因子作为一个组合因子,其相关系数比单一因子高。故本文在挑选因子时,也对因子进行了组合,以提高预报因子的高相关性。按照以上方法,最后共挑选了425个预选因子,其中组合预选因子62个。
2.2 预测因子的选择及机制分析
南下冷空气活动是影响广西前汛期暴雨过程的关键因子之一[36],其中欧亚中高纬地区的环流形势可决定南下冷空气对广西暴雨的影响程度[26]。陶诗言[51]早在20世纪80年代初期就已指出,由于中低纬天气系统相互作用,中高纬度环流型由纬向环流转为经向环流,此时高空槽加深,冷空气南下。为此,欧亚中高纬的高相关影响区是本文的重点关注区域之一。经普查发现,多个高相关因子“负”中心位于鄂霍次克海附近,“正”中心位于加拿大附近(图1a),其中上年5—8月平均鄂霍次克海附近组合因子相关系数最高,高达0.63(表1中预测因子1)。同时,多个因子在北半球极地与中高纬地区呈现“正—负”相关位相,类似北极涛动负位相(图1b),其中前期上年5—7月平均的组合因子相关系数高达0.53(表1中预测因子2)。已有研究表明,北极涛动可引起持续多个月的下垫面(如积雪、海冰和海温等)异常,再反馈到后续的大气环流,并对最初北极涛动异常进行响应[52]。在前期1月500 hPa高度场增量序列与广西6月降水增量序列的相关分布图(图略)上,青藏高原附近地区存在显著负相关区,高原以南为广阔的正相关区,这一组合因子相关系数高达0.54(表1中预测因子3)。同期500 hPa回归风场(图略)上,欧洲和贝加尔湖附近为异常反气旋性环流,高原及其以北地区为异常气旋性环流,有利于高原西风槽和低涡切变的形成,造成1月高原积雪偏多[39]。这一变化可增强冬春季高原近地面热源作用,进而影响后期环流变化[39]。另一方面,前期4月北大西洋从低纬到高纬存在“正—负—正”高相关中心(图略),其中北大西洋低纬地区最大相关系数达0.58(表1中预测因子4)。前人的研究指出北大西洋海温的异常会激发沿欧亚大陆向下游传播的类似于欧亚(EU型)遥相关波列,从而引起其下游东亚地区的大气环流异常[29-31],进而影响华南地区降水。这4个因子回归的当年6月环流均表现为中高纬地区经向环流偏强,有利于冷空气南下,且热带西太平洋地区出现异常反气旋性环流,使得偏南气流将大量水汽向广西输送(图1c、d),有利于广西降水的产生[1]。因此,这4个因子均可作为降水预测的因子。

表1 预测因子及其与广西6月降水年际增量的相关性
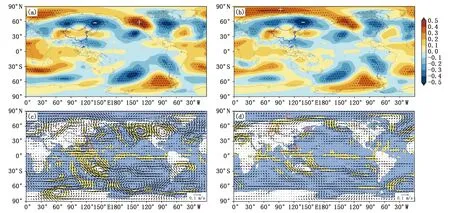
图1 1960—2021年广西6月降水增量序列与前期上年5—8月(a)、前期上年5—7月(b)500 hPa位势高度增量的相关场及预测因子1(c)、预测因子2(d)回归得到的 6月500 hPa 风场年际增量(箭头)(a、b中圆点区域和c、d中黄色区域通过α=0.05显著性检验;c、d中“A”表示反气旋性环流,“C”表示气旋性环流;预测因子释义见表1,下同)
同时,南半球海温及大气环流异常对华南前汛期降水过程有指示意义[30-31]。在预选因子群中,多个“正—负” 组合因子位于东南太平洋至澳大利亚东南侧,多个“正”相关因子位于南半球马斯克林附近,其中前期上年7—8月在南太平洋地区的相关分布最为显著(图2a),从东南太平洋—澳大利亚东南侧—澳大利亚和海洋性大陆地区—华南地区呈现“正—负”交替相关波列,且这一波列在东南太平洋至澳大利亚东南侧的“正—负”组合因子相关系数达0.62(表1中预测因子5)。另外, 前期上年8月南半球马斯克林附近有一显著正相关区域,其相关系数达0.51(表1中预测因子6)。已有研究表明,前期南太平洋海温异常也可通过引起大气环流异常来激发跨赤道遥相关信号,进而影响东亚天气气候变化[30-31]。偏强的马斯克林高压有利于印度尼西亚附近的越赤道气流增强,造成西太平洋副高加强西伸[54]。由这2个因子序列回归的6月500 hPa风场(图2b)上,澳大利亚地区为异常气旋式环流,赤道东风异常明显,有利于越赤道气流的增强,进而增强低层印度洋暖湿水汽向广西输送[53-54],利于广西6月降水偏多。因此,这2个因子的年际增量也可作为降水预测的因子。

图2 1960—2021年广西6月降水增量序列与前期上年7—8月500 hPa位势高度增量的相关场(a)及预测因子5回归得到的 6月500 hPa 风场年际增量(箭头)
综上所述,本文选择了对广西6月降水影响较为明显的6个前期物理量因子(表1),作为建立非线性预报模型的预报因子。
3 集合预测模型的建立与分析
在以往无论是统计集合预报还是数值预报模式的集合预报研究过程中均发现,要提高集合预报模型的泛化能力,必须要求参与集成的预报个体在准确性与差异性之间取得平衡。如何保证参与集成的个体既有一定的预报准确性,又保持他们之间的差异性,对提高集合预报模型的预报能力是非常重要的。为此本文尝试采用有较强处理非线性问题能力的模糊神经网络与熵度量方法相结合来构建月降水年际增量的集合预报模型,并分析模型的预报能力。
3.1 集合预测模型的建立
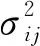

图3 熵度量-模糊神经网络学习过程流程
3.2 预测模型试验分析
以表1的6个预报因子为基础,利用建立的熵度量与模糊神经网络的月降水年际增量集合预报模型,将1960—2013年54个6月降水增量序列作为预报模型的建模样本进行回算拟合检验,然后依次对2014—2021年的 8个独立预报样本作预报检验,其中趋势计算以54年建模样本作为历史同期均值,同号率计算为同趋势样本与总样本的比率。图4为广西6月降水年际增量观测值与年际增量预测值,预测模型回报年份同号率为87.5%,拟合平均绝对误差为26.64 mm,拟合平均相对误差为9.06%,其中相对误差在±15%以内的样本有6个,模型具有较好的回报效果。另外,在8年的独立样本回报预测中,相对误差大于15%的有2个,分别为降水最大值年份(2017年)和降水最小值年份(2021年),相对误差分别为-19.75%和21.86%,对这种极值年份的预测,相对误差在20%左右,且预报其偏多偏少的趋势正确(表2)。可见,本文提出的熵度量与模糊神经网络的月降水年际增量集合预报模型具有较好的精度,可用于对广西6月降水的预测。
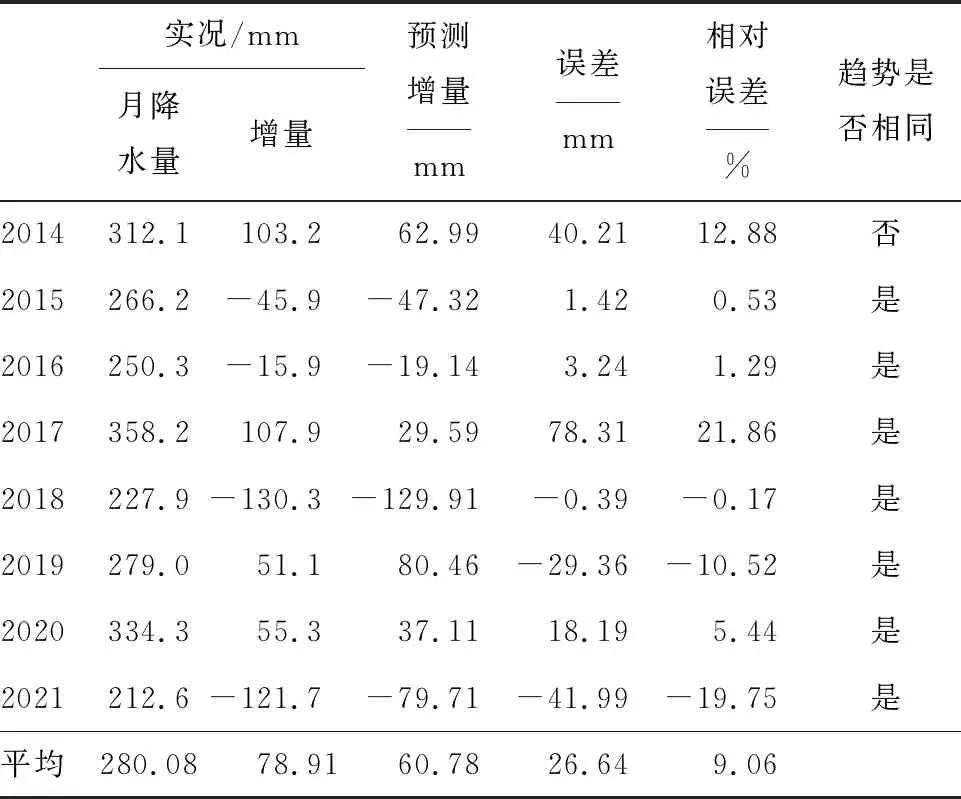
表2 2014—2021年熵度量-模糊神经网络集合预报模型独立样本回报检验结果

图4 1960—2021年广西6月降水年际增量观测值与熵度量-模糊神经网络集合预报模型所获得的年际增量预测值
3.3 预报模型对比分析
为了进一步对比采用熵度量与模糊神经网络的月降水年际增量集合预报模型与线性统计模型的预报性能差异,本文同样以表1的6个初预报因子为因子集,利用同样的建模样本和回报预测检验样本,采用逐步回归方法,建立了逐步回归预报方程:
Y=-0.655606 +1.369157X1+0.561213X2+0.883575X3+2.403222X4+0.246096X5+0.555309X6
预报结果见图5和表3。相比于熵度量-模糊神经网络集合预报模型,逐步回归独立样本拟合平均绝对误差37.68 mm,拟合平均相对误差13.23 %,较模糊神经网络集合预报模型的拟合平均相对误差(9.06 %)有所增加,其中2015年,2016年,2018年,2019年,2020年的拟合相对误差增加明显。可见,本文提出的熵度量与模糊神经网络的月降水年际增量集合预报模型较逐步回归方法回报效果好,模型更稳定。
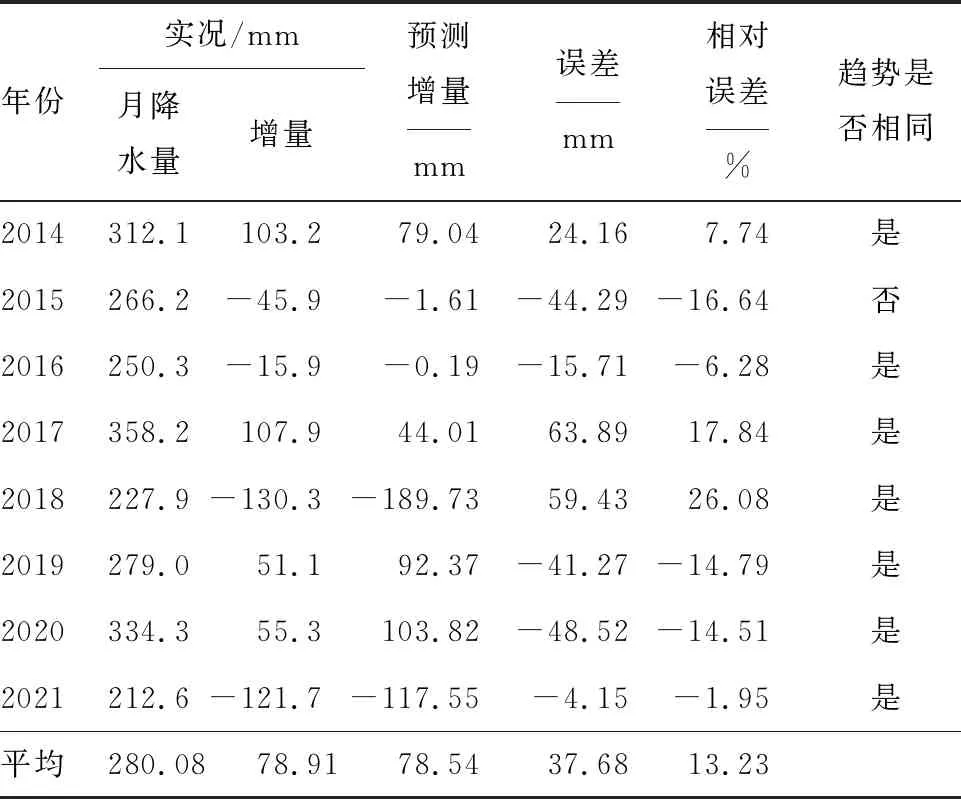
表3 2014—2021年逐步回归方法独立样本回报检验结果
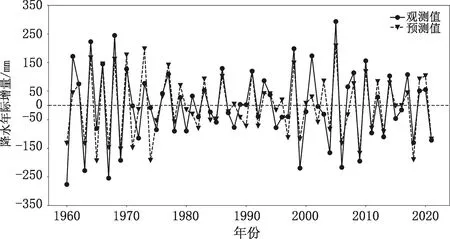
图5 1960—2021年广西6月降水年际增量观测值与逐步回归方法所获得的年际增量预测值
4 结论与讨论
通过普查1960—2021年广西6月降水年际增量与前期大气环流场的相关性,选取了影响广西6月降水异常相关性较高的前期预测因子,采用模糊神经网络与熵度量相结合的方法构建月降水年际增量的集合预报模型,通过对该模型的预测效果进行分析和检验,得出主要结论如下:
(1)从本文挑选的影响广西6月降水的6个主要前期影响因子来看,广西6月降水受南北半球大气环流系统的共同影响,可以挑选相关系数较高、物理意义较明确的影响因子作为建模因子。同时,为得到相关性更好、更稳定的因子,可以使用组合方法对相邻近的因子进行组合。
(2)基于年际增量法建立的广西6月降水熵度量-模糊神经网络集合预测模型,能有效结合熵度量信息增益作用和遗传算法全局优化的能力,表现出较好的预报性能。该预测模型在对2014—2021年独立样本回报检验中,预测模型的回报年份同号率为87.5%,拟合平均绝对误差为26.64 mm,拟合平均相对误差为9.06 %。
(3)通过对比分析发现,利用非线性的熵度量-模糊神经网络方法建立的集合预报模型,在相同的预报因子条件下,预报能力和稳定性明显优于用逐步回归方法建立的预报模型。
影响广西6月降水的因素较为复杂,冬春季海温、积雪、海冰等因素对广西降水也有影响[25-31]。本文在建模挑选影响因子时,着重考虑了500 hPa大气环流的影响以及预选因子与预报量序列相关系数的大小,但部分影响机制不是特别清晰,如前期上年5—8月平均鄂霍次克海附近的组合因子通过何种方式调节当年6月的环流还不太清楚,有待进一步开展分析研究。在今后的研究中,还需进一步结合动力模式资料挑选的同期大气环流因子或者利用冬春季海温、积雪、海冰等关键区作为预测因子,利用本研究所使用的模糊神经网络与熵度量相结合机器学习方法来建立预测模型,并与本研究结果对比分析,进一步加深对该模型的理解与应用。另外,机器学习方法是以大数据为基础的自适应学习方法,要尽可能使用最大样本数据,建模样本数过少可能会减少预报方法的可靠性。而气候模式(CFS和Derf2.0等)回报资料多从90年代开始,若使用气候模式产品,则建模样本数过少。因此如何更好地利用现有的更具物理意义的模式产品资料数据也是智能计算机器学习方法需要深入研究的课题。
