空间自由曲面砌体拱壳的结构设计与试验研究
2024-04-19刘博伟陈剑峰来武清郑良平赵雪冰封竺汐孔德坤
刘博伟, 陈剑峰, 杨 越, 来武清, 郑良平, 赵雪冰, 封竺汐, 孔德坤
(中机中联工程有限公司,重庆 400039)
0 引言
自由曲面结构由于其优秀的表现力,逐渐受到建筑师的青睐,成为了空间结构的一个重要发展方向。而壳体结构多为自由曲面的基本结构形态。国外对于此类结构研究较早。早在1968年,瑞士工程师Heinz Isler在某一加油站[1]中就应用了薄壳结构,如图1所示,该壳体跨厚比达到400,至今已经有50余年,依然没有出现大的裂缝。随后,Heinz Isler又于1973年、1982年、1987年分别设计了花卉中心、索尔图恩布鲁尔体育中心、空军博物馆等多个薄壳曲面结构。

图1 Deitingen高速公路服务站[1]
近年来,此类薄壳结构也逐渐受到国内建筑师的欢迎,典型工程案例有山西大同大剧院[2]、武汉市琴台美术馆[3]、乌镇互联网峰会“红亭”[4]。此类壳体结构规则性较好,容易布置钢筋,能较好地满足受力与变形的要求。
本文以无筋自由曲面砌体拱壳结构——重庆市黄桷坪涂鸦街美术廊(图2)为背景,介绍自由曲面的结构分析和设计,以期为相关工程提供案例参考和设计思路。

图2 项目实景图
1 薄壳结构研究现状
所谓的“自由曲面”,是指不能通过解析式表达或者无法由简单曲面组合的曲面形状,它是一种正负高斯曲面的有机结合[5],在机械领域应用较多。自由曲面在应用于建筑领域中时,要考虑的问题是力学上的合理性[6],因此创建出既满足建筑意图同时又满足结构受力要求的曲面形状是首先要解决的问题。早期的建筑师大多采用物理模型试验的方法,例如西班牙建筑师Antonio Gaudi采用“逆吊试验法”设计的圣家族大教堂[7],瑞士工程师Heinz Isler采用“薄膜充气法”设计的瑞士合作配送中心[8],德国建筑师F.Otto[9]利用“肥皂薄膜法”设计的慕尼黑奥林匹克体育馆,意大利工程师S.Musmeci设计的高架桥[10]等。这些物理试验的方法为曲面形态的创建提供了丰富的参考,但由于试验的制约因素,此方法精度较低,并且未经过严格理论层面的力学推理。
随着计算机技术的发展,计算机对结构设计起到了巨大的推动作用,曲面形态的找形也脱离了单一的试验手段。Schek[11]提出力密度分析法(FDM法),该方法基于最小曲面理论,以拉索单元模拟曲面的应力,以拉索达到平衡状态时的形状来确定结构的最高效形状;Philippe Block[12]基于力密度法提出推力线网格法(TNA法),该方法是利用形图解和力学图解交互作用来生成壳体的形态,其方法思路是首先确定壳体的边界,然后在壳体水平投影上绘制网格,再根据想获得的壳体形态绘制对应的力图解,之后不断调整形图解和力图解的图像,在二者共同作用下逐渐逼近最终壳体形态,基于此理论,在Rhino平台开发了RhinoVault程序,该程序可快速绘制形图解和力图解的图像,达到快速找形的目的。TNA法的缺点在于,只能基于水平面上的网格进行找形,并且调整过程较为繁琐。不同于TNA法,粒子弹簧系统分析方法(PSS法)可以对三维曲面进行优化,PSS法是基于动力学的一种方法,又称动力松弛法,该方法将曲面离散为很多个粒子,每一个粒子根据网格划分集中了单元的质量和速度,粒子之间通过有一定刚度的弹簧连接,粒子所受的力为外力和弹簧内力;通过改变外力,设置粒子与粒子之间的引力或者斥力等方式,模拟曲面的力学表现。梁道轩和侯胜利[13]对FDM法、TNA法、PSS法做了总结,认为FDM法和TNA法可以适用于体型较为复杂的项目。
国内对壳体找形的研究更多偏向于函数解析方式,崔昌禹和严慧[14]提出高度调整法,该方法将曲面高度与结构的应变能建立函数关系,通过观察应变能对曲面高度的敏感程度来调整高度,最终使应变能敏感度趋于0,并基于此方法,设计了西班牙BLANES国际会议展示馆和日本北方町多功能活动中心。武岳等[15]将逆吊试验思想与计算机数值模拟相结合,提出了“数值逆吊法”,利用非线性有限元技术实现结构形状的精确控制,其思路类似于PSS法。
总体来说,找形方法以早期的物理试验法为基础,在计算机技术的推动下,衍生出了许多新的函数解析形式的找形方法并均有相应的工程案例。
2 工程概况
重庆市黄桷坪涂鸦街美术廊为一高度自由旋转的薄壳结构,较难配置钢筋。为满足高跨厚比、无柱、视觉等要求,选用砖砌拱壳结构体系。拱壳总建筑面积为360m2,总长45.9m,最大矢高5.2m(图3),最大宽度为17.3m,为保留树木设置有不规则开洞,洞口直径约为1.42m(图4)。整个壳体厚度为90mm,且未配置钢筋,为目前国内跨度最大的无筋自由曲面砌体拱壳。

图3 项目结构前视图

图4 项目结构洞口
2 找形分析
本项目基于设计角度,从TNA法入手,采用Rhino软件,首先根据建筑方案确定壳体平面边界,边界分为两种:洞口边界和支座边界。之后对平面“壳体”进行网格划分作为初始的形图解。之后进行形图解与力图解的交互,确立出壳体的初步三维结构形态,过程如图5所示。
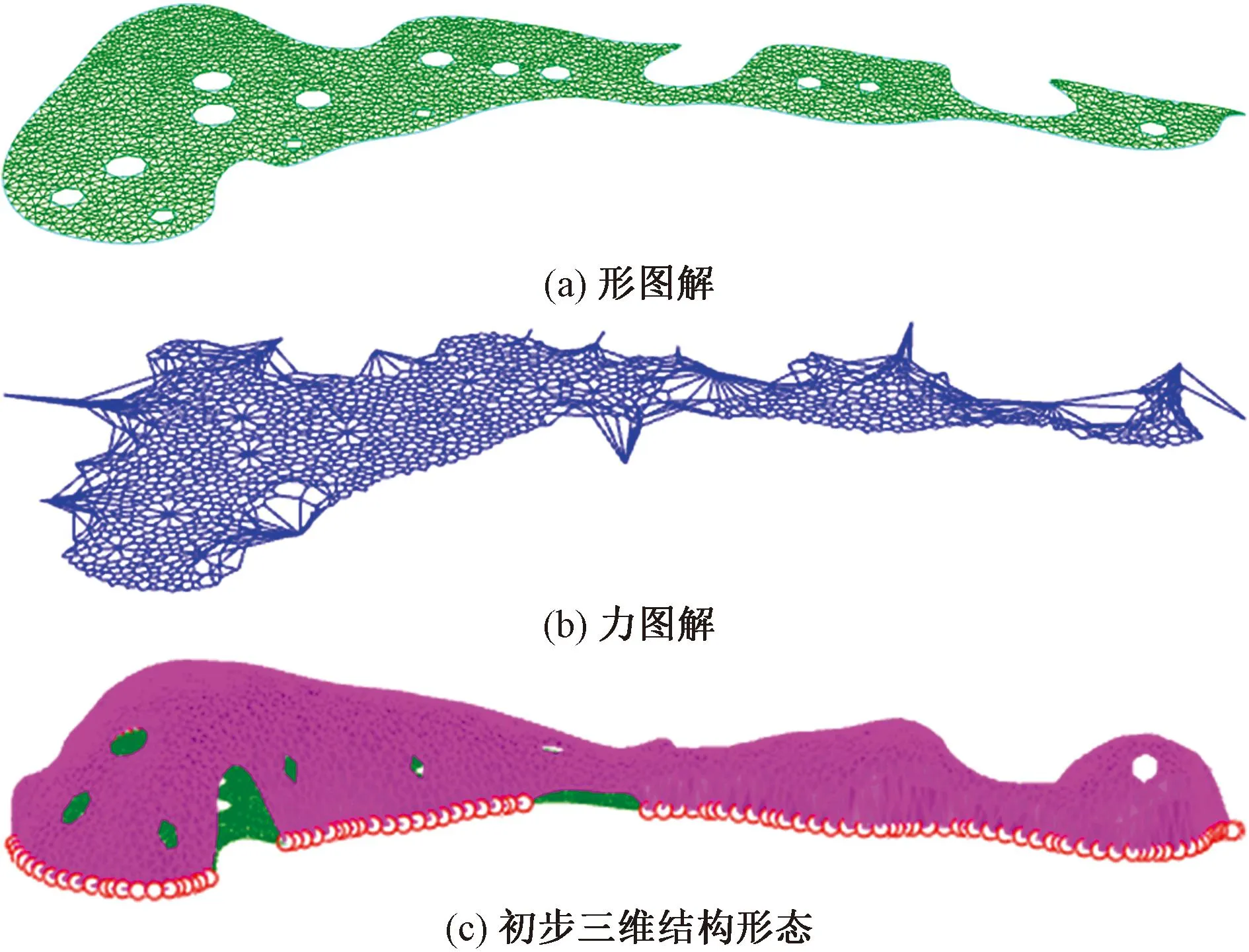
图5 TNA法确认壳体初步形态过程
确立此项目的初步结构形态后,采用PSS法对初步结构形态进行进一步优化,调整区域内力以逐渐逼近基于初步结构形态提出的建筑形态(图6)。

图6 采用PSS法调整后的结构形态
由于建筑形态要求较高,PSS法优化后的壳体结构形态在局部依然无法满足建筑方案的要求,根据壳体内力计算结果与建筑方案进行反复调整,最终确立出壳体的形态。
3 材料与砌筑工艺研究
本壳体材料采用多孔陶土砖和高延性混凝土砌筑,多孔陶土砖尺寸为200mm×100mm×30mm,砌块粘结砂浆为Cd50高延性混凝土,厚30mm。高延性水泥基复合材料(engineered cementitious composite, ECC)最初由美国密西根大学的Li[16]等提出,该材料在抗拉、抗剪、抗弯等方面表现出良好的韧性和耐损伤能力。目前国内外已将其应用于隧道、桥梁等加固修复中[17]。国内西安建筑科技大学对ECC展开了大量的研究。邓明科等[18-19]采用ECC设计理念配置了高延性混凝土(high ductile concrete,HDC),并研究了HDC对无筋砖砌体墙加固后的抗震性能,结果表明HDC加固可显著提高墙体的承载力和位移延性。本工程委托西安建筑科技大学高延性混凝土材料与结构研究所对多孔陶土砖与高延性混凝土砂浆的复合材料进行力学性能试验研究。试验构件受力尺寸宽220mm、长620mm,厚度与实际工程相同。试验构件如图7所示,加载方式如图8所示。

图7 试验构件

图8 加载方式
试验结果表明,两种加载方式对试验结果无明显影响。加载初期,构件处于弹性阶段,高延性混凝土和多孔砖共同工作,当荷载加至约为峰值的50%时,砖出现裂缝,很快下侧砖断裂,但砂浆与砖体依然粘结良好,随着荷载增加,高延性混凝土逐渐出现多条裂缝,随着变形不断增大,荷载增幅越来越小,直至裂缝延伸至上层砖,构件破坏。该复合砌体材料在受力过程中,表现出良好的弹性和位移延性,并且根据试件破坏现象来看,试件在受力过程中,砂浆与砖的粘结性能良好,从始至终砖体未发生剥离、掉落现象,构件表现为共同受力。试验测得试件最小抗弯强度为8.44MPa。同组3个相同构件荷载-位移曲线如图9所示,最终破坏如图10所示。

图9 构件荷载-位移曲线

图10 复合砌体受弯最终破坏现象
为保证壳体完成形态与设计计算形态相符,该项目砌筑方案采用内置胎膜方式。按壳体形态,内部每隔250mm设置木板支撑,支撑之间搭设钢筋作为临时支撑,以木板+钢筋搭建出的曲面作为壳体的胎膜。木板形状利用Rhino软件切割壳体获得,如图11所示(图中红色为钢筋,灰色为木板)。
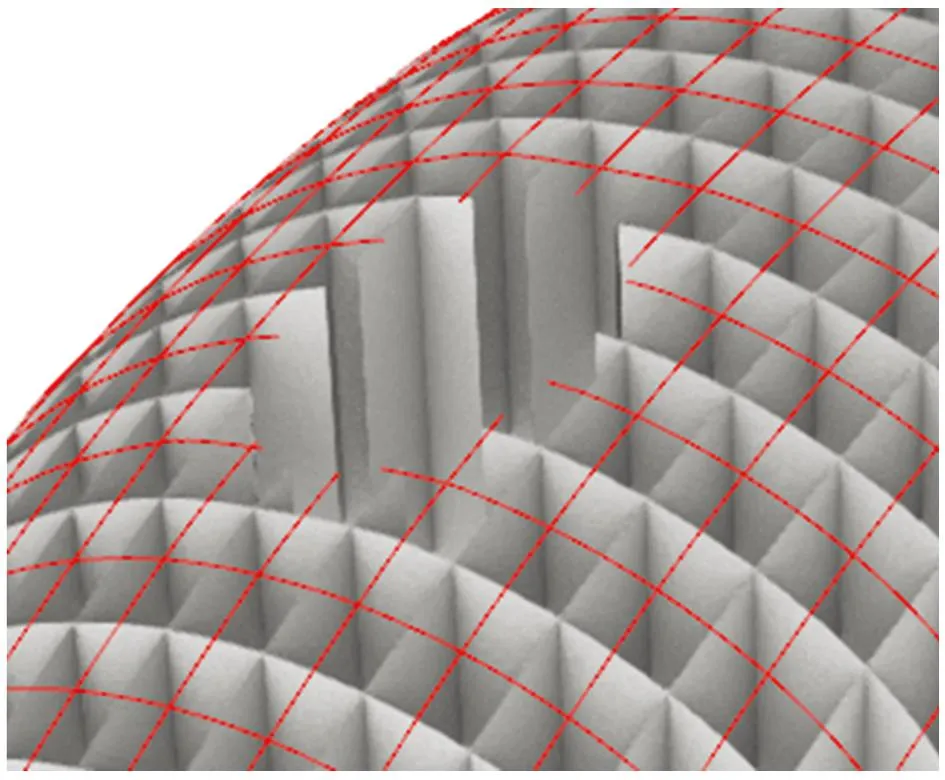
图11 壳体胎膜制作
施工时,设置好胎膜后,首先铺设第一层砖(图12),待到砖缝砂浆凝固后,再同时铺设砂浆与第二层砖。养护28d后,再拆除胎膜。

图12 壳体施工图
4 结构弹性设计与分析
4.1 计算参数
本项目结构计算分析软件采用MIDAS Gen进行分析,采用SAP2000进行校核。由于材料表现出良好的弹性和整体性,本项目计算采用各项同性材料模拟,模拟单元为壳单元,材料参数如表1所示。

表1 计算模型材料参数
本工程功能为艺术展厅,上部不上人。主要考虑恒载、活载、温度作用。恒载主要为自重。活载为不上人屋面0.5kN/m2,同时活载考虑最大跨的半跨不利布置工况。项目在5月份施工,根据《建筑结构荷载规范》(GB 50009—2012)可知,重庆市月平均最高气温为37℃,月平均最低气温为1℃,取结构合拢温度为19℃,考虑温度荷载,取其值为±25℃。项目所在地为抗震设防烈度6度(0.5g)区,场地特征周期为0.35s,结构阻尼比取0.05。本项目荷载较小,对基础造成的不均匀沉降较小,本文不作赘述。
由于结构为自由曲面并有不规则开洞,计算模型采用三角形网格,网格尺寸约为0.2m。计算模型如图13所示。

图13 计算模型
4.2 分析及计算结果
两种软件计算的在恒载作用下壳体顶应力云图如图14所示,其中压应力为负,拉应力为正,余同。两种软件分析结果显示,整个壳体应力较小且分布均匀,两种软件应力云图分布几乎相同,最大应力误差为7.5%,可认为壳体整体形态较好。计算结果显示,恒载、活载和温度为壳体的主要控制荷载。本文仅展示这些荷载作用下的计算结果。
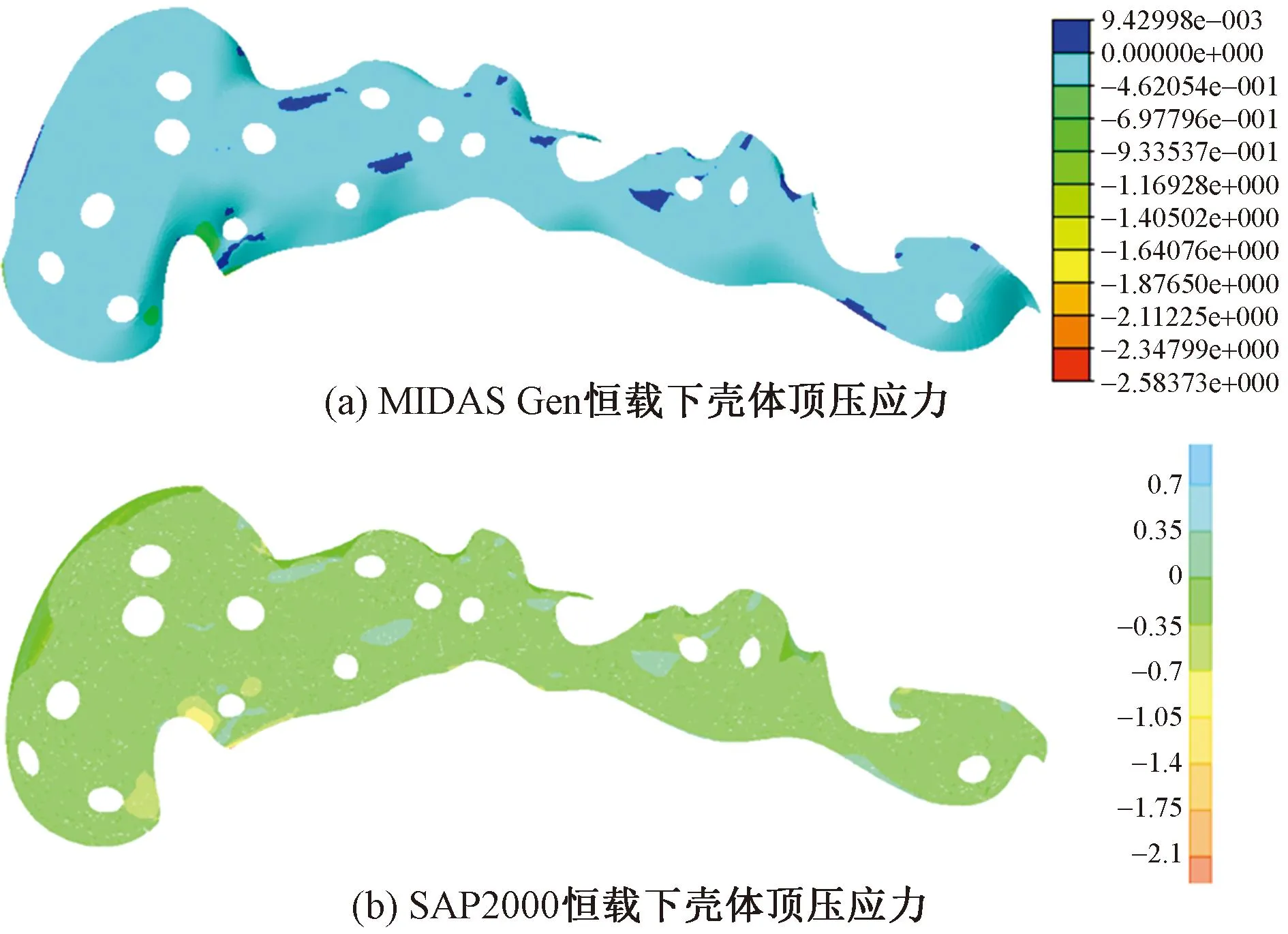
图14 壳体顶底应力云图/MPa
4.2.1 壳体应力
在竖向荷载下,壳体主要表现为受压与受弯状态,材料抗压强度远超抗弯强度,本文仅展示壳体受拉应力状态。各控制工况下壳体底、顶拉应力如图15所示。
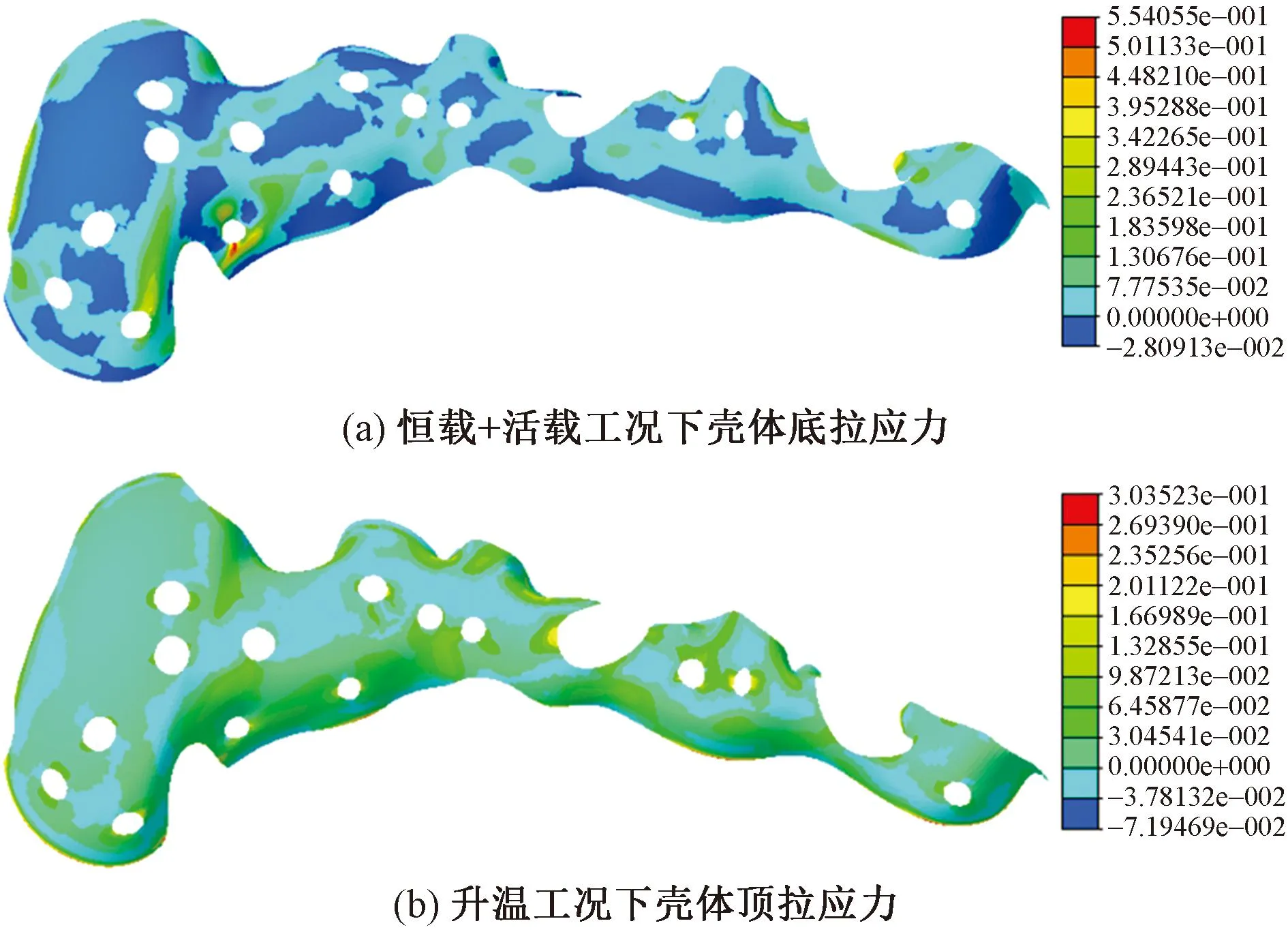
图15 壳体拉应力云图/MPa
在恒载+活载工况下,壳体拉应力出现在壳体底部,最大为0.55MPa,位置为左侧入口处,该区域为满足开洞及入口的形态,局部受力面积较小,其他位置受力较为均匀,约为0.10MPa。在升温工况下,壳体拉应力出现在顶部,最大为0.03MPa,其他区域拉应力较小,约为0.08MPa;升温时,壳体膨胀,拱顶有向上变形趋势,因此顶部出现拉应力。
4.2.2 壳体变形
由于壳体为自由曲面,变形表现为空间变形,本文所述变形均为空间法向变形。壳体不同工况下变形如图16所示。
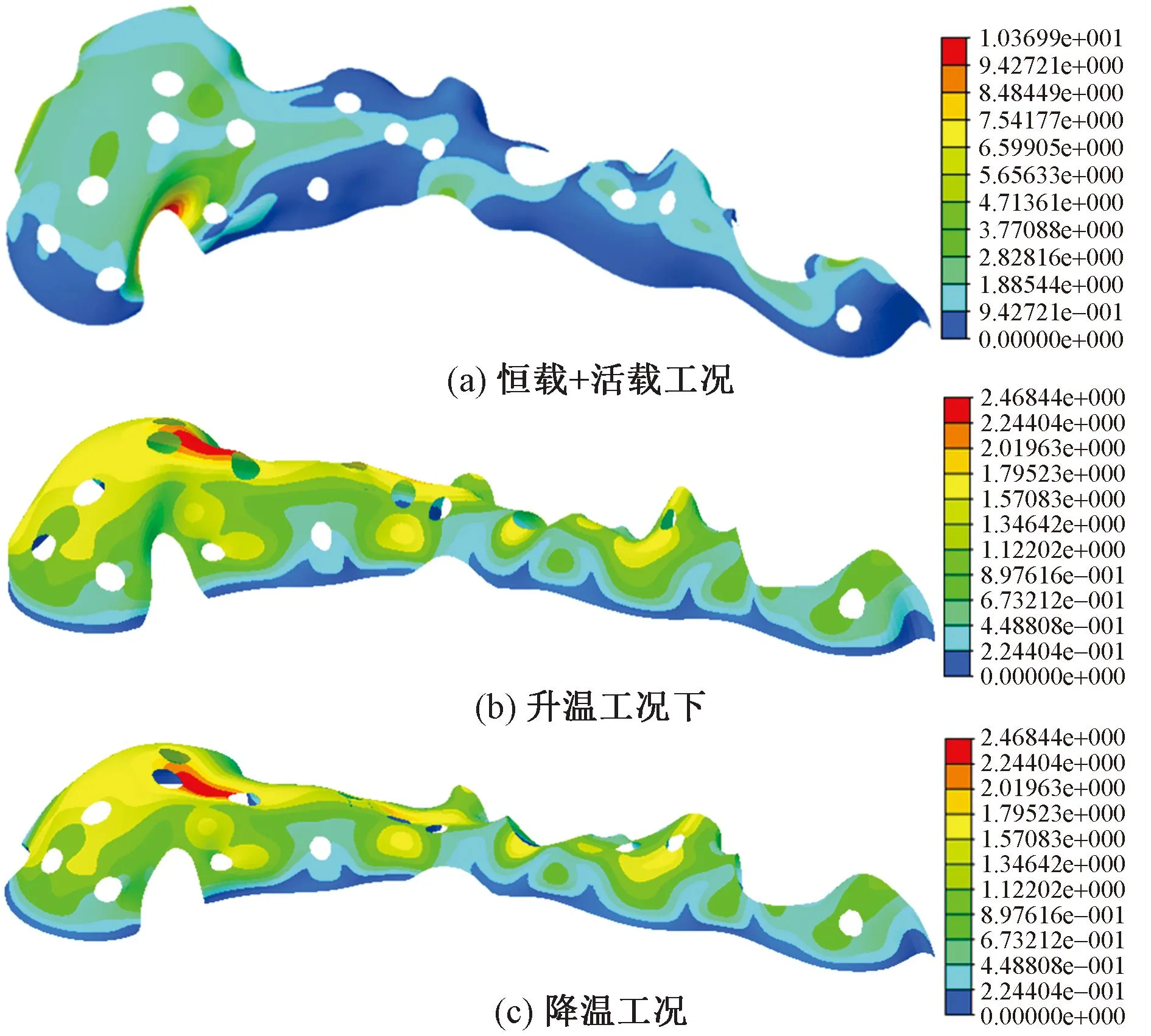
图16 壳体变形云图/mm
恒载+活载工况下,壳体最大变形出现在左侧入口顶部,约为10.36mm,由于需要为入口保留足够空间,入口位置均为壳体的薄弱部分,变形均相对较大。温度变化时,壳体最大变形均出现在最高处拱顶,这是由于材料随着温度变化而收缩或膨胀,材料收缩时,拱顶两侧受拉,拱顶“下陷”,材料膨胀时,拱顶两侧受挤压,使得拱矢高进一步增大。
4.3 壳体稳定性研究
对于薄壳结构,应进行稳定性计算[20]。本项目利用MIDAS Gen软件进行屈曲分析,假定材料为弹性。首先采用恒载+满布活载方式进行屈曲分析,一阶屈曲模态如图17所示。恒载+满布活载下壳体屈曲因子约为14.81。

图17 一阶屈曲模态
根据恒载+满布活载下的一阶屈曲模态,布置半跨活载(图18红色区域)。恒载+半跨活载下壳体屈曲因子为14.57,屈曲模态与恒载+满跨活载下的屈曲模态类似,本文不再予以展示。

图18 恒载+半跨活载屈曲分析的活荷载布置
考虑满跨活载下的一阶屈曲模态的初始缺陷进行几何非线性分析,缺陷变形最大值为56mm(为最大横向跨度的1/300),壳体最大位移处的荷载-位移曲线如图19所示。考虑几何初始缺陷分析模型,稳定因子接近14,表明结构稳定性满足要求。
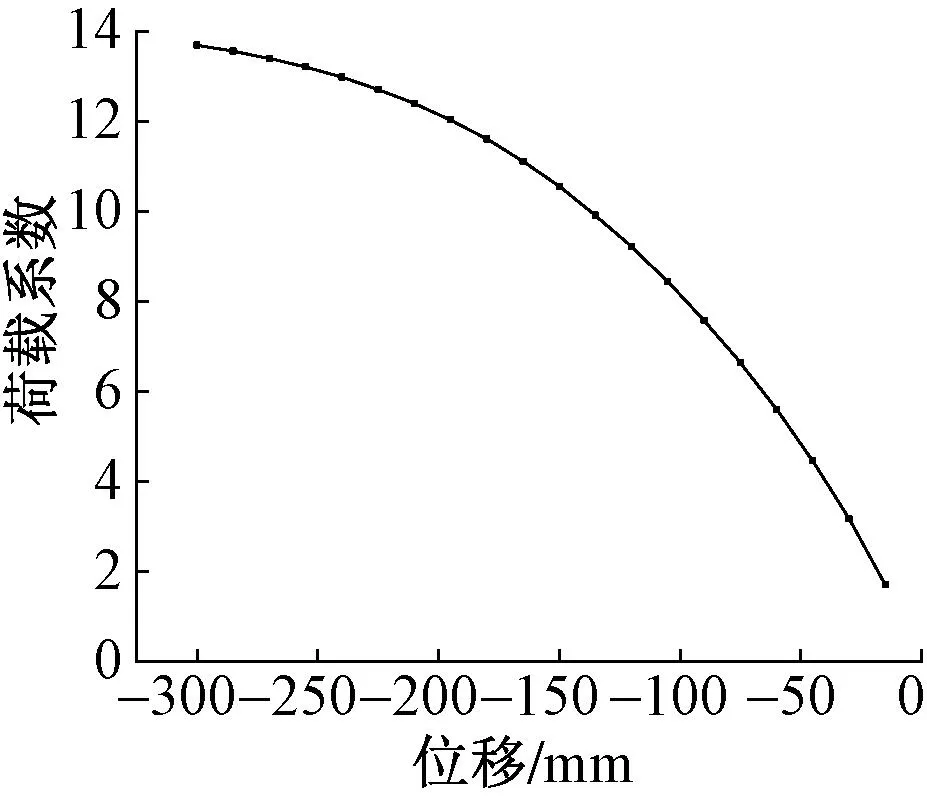
图19 壳体最大位移处荷载-位移曲线
5 足尺荷载试验
本项目作为目前国内跨度最大的无筋砖砌自由曲面拱壳,为保证工程的安全性,对壳体进行足尺加载试验。试验根据实际情况以及最不利荷载工况布置荷载,在壳体矢跨比较大一端采用沙袋方式分级加载,每级加载0.15kN/m2,最终加载至0.75kN/m2。试验加载现场如图20所示,加载范围见图21中红色区域。

图20 试验加载现场

图21 加载范围
根据4.2节位移以及应力的计算结果分别布置测点,见图22,其中位移测量精度为0.001m。

图22 测点布置图
由于壳体受温度作用影响明显,试验前首先采用红外点温计对壳体进行空载温度测试,位移测点与应力测点温度敏感度结果见表2、3(降温时指标变化相反)。

表2 位移测点在升温1℃时位移变化
表2、表3显示,由于壳体的形态不规则,不同位置在单位温度变化下位移和应力的敏感程度不同,试验时,不同测点结合加载前后温度变化对试验结果进行修正。

表3 应力测点在升温1℃时应力变化
试验工况下壳体位移和拉应力计算结果见图23。壳体最大空间位移为1.688mm,方向为壳体下侧。壳体底部最大拉应力约为0.09MPa。根据试验工况下的计算结果(图23),位移和应力均应重点关注测点2位置。

图23 试验工况下位移和拉应力计算结果
测点2位移和应力实测值与计算值对比见图24,各测点位移和应力实测值与计算值对比见表4。由图24及表4可见,计算所得的位移、应力曲线变化趋势与实测的基本一致,不同荷载步下变化程度大小一致;位移、应力计算值大于实测值,因此计算结果偏于安全。

表4 位移和应力实测值与计算值对比

图24 测点2位移、应力实测值与试验值对比图
6 结语
本项目经过找形优化、材料试验、计算分析和足尺荷载试验等,验证了自由曲面砖砌壳体的安全性,具体总结如下:
(1)采用推力线网格法和动力松弛法,利用竖向荷载对壳体找形,所确定的结构形态受力性能较好,此找形方法可应用于相应的结构方案设计阶段。
(2)采用TNA法和PSS法找形时,初始网格对找形结果有一定的影响,类似项目在进行相关设计时,在找形前需要尽可能均匀地划分网格。
(3)地震作用下本工程结构应力及变形均较小,对于地震工况下的结果并未展示,而实际地震作用为动力工况,后续可以对材料进行动力响应下的损伤分析,从而可以更准确地确定壳体安全性。
(4)本项目结构分析时采用壳体单元,将材料假定为各项同性材料,对实际材料进行了简化。试验结果表明,计算值均大于试验值,因此设计取值偏于保守,壳体安全性有一定的储备。
