X形软钢阻尼器延性断裂的试验研究与数值模拟*

2024-04-19谢丽宇仝运佳薛松涛

建筑结构 2024年7期

谢丽宇, 仝运佳, 薛松涛,2, 李林, 王兵

(1 同济大学结构防灾减灾工程系，上海 200092；2 日本东北工业大学工学部，仙台982-8577)

0 引言

软钢阻尼器的滞回特性稳定,低周疲劳特性良好,且不受环境温度的影响,在抗震设计中得到了广泛的应用[1]。文献[2-4]对各种形式的软钢阻尼器进行了试验研究,验证了软钢阻尼器的性能和破坏形式。在大应变循环作用下,软钢阻尼器容易发生超低周疲劳损伤破坏,即使在较小的应变循环作用下,阻尼器也会由于累积塑性变形而产生损伤。

在1994年的北岭地震和1995年的阪神地震中,出现了较多钢试件发生延性断裂的现象,由于计算机的计算能力有限,很少对延性断裂进行模拟,随着计算机计算能力的增加,延性断裂的模拟变成可能,一些研究工作也致力于阐明钢试件的失效机理[5]。

Mcclintock[6]提出材料空穴的形成与扩张是钢材延性断裂的根本原因,将空穴简化为圆柱形,并对简化模型进行了分析,提出了相应的微观断裂模型。Rice 和Tracey[7]提出了球形和椭球形空穴形核与聚合的模型,分析了空穴的演化规律,指出材料延性断裂由应力三轴度决定,并提出了空穴扩张断裂模型。Kanvinde[8]提出了适合材料超低周往复荷载作用下的微观机制模型,并将其推广应用至钢试件的循环加载断裂模拟分析中。Xue-Wierzbicki损伤起始准则[9]认为累积等效塑性应变是钢材应力与刚度退化的主要原因,但该准则需要试验确定的参数较多。Yu[10]简化了应力三轴度与等效塑性损伤应变的关系,与原Xue-Wierzbicki损伤起始准则中的路径偏离程度不大。

为了准确模拟软钢阻尼器的破坏机理,本文设计了6组试验,并基于材料微观损伤模型对其进行了精细的有限元模拟,以验证简化的损伤准则在描述软钢阻尼器承载力退化与损伤发展中的适用性。

1 基于应力三轴度的钢材微观损伤模型

1.1 损伤起始准则

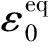
(1)

式中:a1、a2分别为钢材纯剪(η=0)、钢材单轴拉伸(η=η0)对应的等效塑性损伤应变,a1和a2可通过单轴拉伸试验确定;η0为常数,取为1/3。

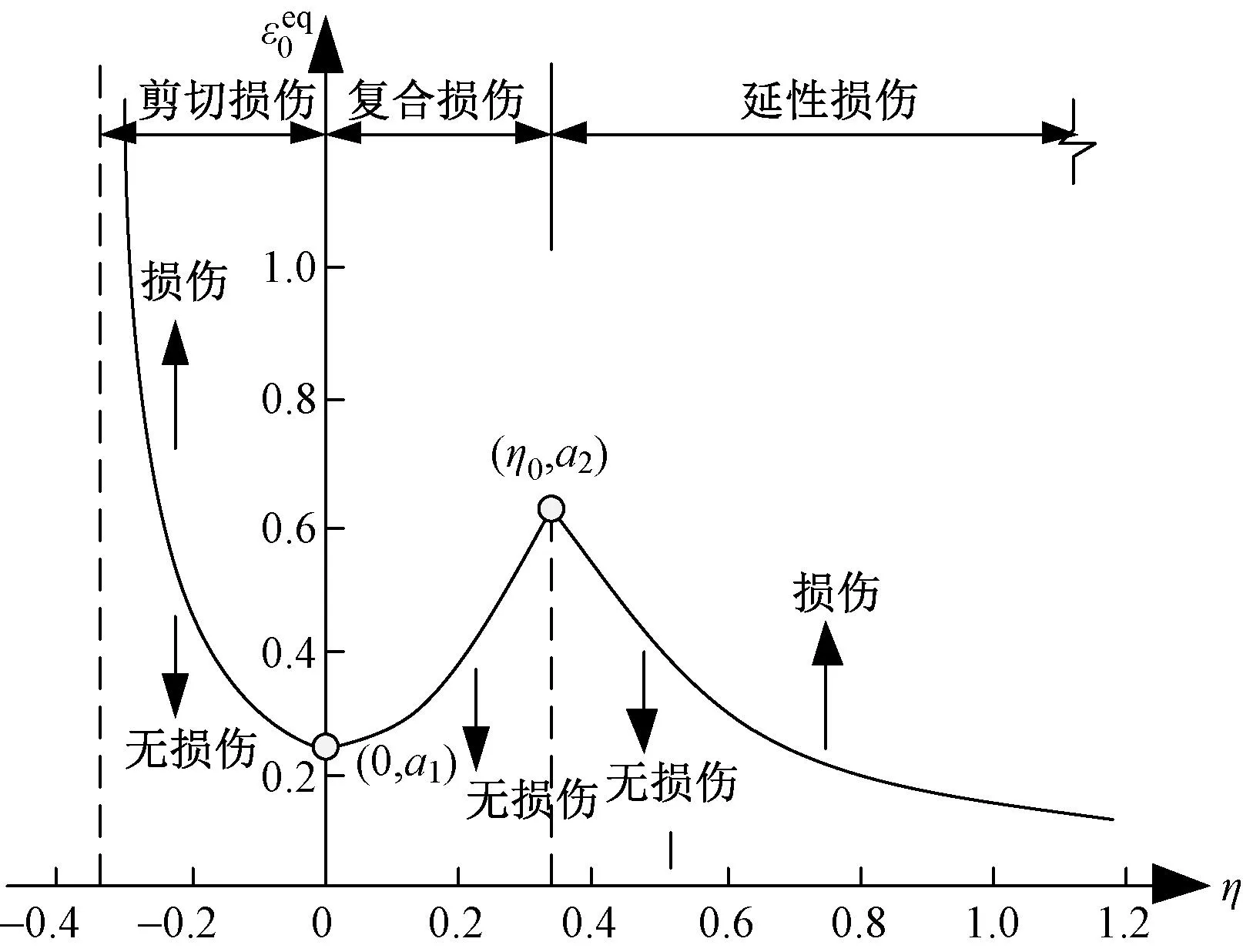
图1 等效塑性损伤应变与应力三轴度的关系

Xue-Wierzbicki[9]认为等效塑性应变是损伤产生的原因,当累积等效塑性应变满足式(2)时,钢材中的微裂纹开始发展,材料内部发生损伤。

(2)

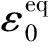
图2 延性损伤模型示意图

1.2 损伤演化准则

损伤起始准则给出了钢材开始发生损伤的时刻,但未给出钢材损伤后应力下降的路径,引入损伤因子D来表征钢材的损伤程度,当D=0时,钢材无损伤,当D=1时,钢材完全断裂破坏。钢材在应力下降区段的剩余模量Ee及剩余应力σe可表示为损伤因子D的函数:

(3)

钢材发生损伤后,应力-应变关系不再能准确地描述材料的力学行为,继续使用钢材的应力-应变关系会引入强烈的基于局部应变的网格依赖性[11],为了减小单元的网格依赖性,采用基于位移的损伤演化路径。引入单元特征长度L(L对于实体单元可取体积的立方根)将钢材的等效塑性应变εeq表示为钢材的等效塑性位移ueq的形式:

(4)

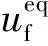
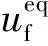
(5)

为了确定式(5)的函数形式,周天华等[12]通过对10组钢材试件进行拉伸试验,获得了钢材的真实应力-应变曲线,然后对每条真实应力-位移曲线下降段的剩余应力与塑性位移进行了无量纲的归一化处理,得到了钢材剩余应力比与塑性位移比的相关曲线,损伤因子D的表达式为:

(6)

2 X形软钢阻尼器试验研究

2.1 试件的设计

X形软钢阻尼器试件共6组,尺寸相同,厚度均为20mm,阻尼器材料为LY225低屈服钢材,其他固定装置采用Q235。软钢阻尼器两端通过高强度摩擦型螺栓与固定装置连接,以形成端部固定约束。试件采用线切割加工工艺,可尽量降低钢材内部的残余应力,软钢阻尼器的尺寸和实物图见图3。

图3 软钢阻尼器尺寸与实物图/mm

2.2 试验方案

试件底部固定,顶部只允许面外的水平位移。变幅加载制度见图4,变幅加载初始幅值为20mm,小于等于70mm时每级幅值增量为10mm,超过70mm时每级幅值增量为5mm。试件编号由字母和数字构成,第一个字母代表加载方式,M代表单调加载,V代表变幅加载;数字代表在每一个幅值下加载循环的次数。因此,试件编号M-1 表示单调加载至破坏;试件编号V-1、V-2、V-3、V-4 分别表示变幅加载至破坏,见图4;试件编号C-1 表示幅值45mm加载30圈,幅值55mm往复加载7圈,再变幅加载直至破坏。

图4 变幅加载制度示意图(加载次数n=3)

3 试验结果分析

3.1 破坏过程

X形软钢阻尼器经历表面氧化皮剥落、残余变形累积、颈部过渡区域局部屈曲、颈缩和断裂五个阶段。

第一次循环加载后,阻尼器表面氧化皮即全部脱落;幅值较小(<50mm)的循环加载过程中,残余变形较小,集中在颈部区域;幅值较大时(≥50mm),残余变形逐渐累积,此时颈部区域发生局部屈曲现象,见图5;最后阻尼器颈部发生颈缩,颈部发生延性断裂,见图6。试验结果表明,颈部为阻尼器的薄弱部位,在阻尼器的设计中,应选择合适的颈部宽度,保证在罕遇地震作用下颈部区域不发生破坏。

图5 颈部屈曲变形

图6 颈部破坏

3.2 荷载-位移曲线

各试件的荷载-位移曲线见图7、8。试件V-1～V-4为变幅加载,由图7可知:1)在弯曲变形阶段,滞回曲线饱满,试件具有较好的耗能能力;2)在弯轴变形阶段,滞回曲线明显上扬,这是由于在大位移作用下,轴力与弯矩共同影响;3)滞回曲线表现出明显的循环强化及随动强化特性;4)试件在弯轴变形阶段末端,具有较明显的损伤退化,说明较大的累积塑性变形将对阻尼器性能产生劣化效应。

图7 循环加载试验与有限元结果对比图

试件M-1为单向加载直至破坏,由图7可知:试件M-1经历弹性阶段、承载力缓慢上升阶段(弯曲变形阶段)、承载力快速上升阶段(弯轴变形阶段)和退化阶段。荷载-位移曲线快速上升是由于当水平位移达到一定数值时,阻尼器不再为弯曲屈服型,轴向力的影响增加,轴向力会让截面更多区域进入屈服甚至达到强化阶段。对于试件M-1,位移达到35mm时需考虑轴向变形对试件的影响。

试件C-1经历了30圈幅值为45mm的循环加载、7圈幅值为55mm的循环加载以及3圈变幅加载。由图7可知:1)试件前30圈滞回环面积变化不大,表明软钢阻尼器疲劳性能良好,具有稳定耗能能力及工作性能,满足《建筑抗震设计规范》(GB 50011—2010)关于位移型消能器设计位移幅值下往复循环30圈后,消能器主要设计指标误差和衰减量不应超过15%,且不应有明显疲劳现象的要求;2)在7圈幅值为55mm的循环作用下,滞回曲线仍较稳定,损伤退化发展较小,表明阻尼器在大位移作用下依旧具有稳定的工作性能;3)试件在第2圈变幅加载过程中,表现出明显的损伤退化现象,表明较大的累积塑性变形将对阻尼器性能产生劣化效应。

4 数值模拟

4.1 有限元模型

为了对软钢阻尼器破坏过程进行准确模拟,并验证基于应力三轴度的钢材损伤和演化准则适用性,采用有限元分析软件ABAQUS作为分析工具。单元类型采用C3D8R,在厚度方向划分4个网格,颈部区域采用细化网格。在阻尼器两端分别建立参考点,参考点与端部约束区耦合,约束参考点的6个自由度,加载方案与试验方案一致。

采用Lemaitre-Chaboche[13]混合强化模型来模拟材料的循环塑性流动,该模型包括等向强化部分和随动强化部分,各向同性强化表征了屈服面大小的扩张,其为等效塑性应变εeq的函数:

dR=b(Q∞-R)dεeq

(7)

式中:R和dR分别为屈服面大小的变化值和增量变化值;Q∞为屈服面大小的最大变化值;b为描述各项同性强化率的材料参数。

本文参考严红[14]关于LY225钢材各向同性强化参数的取用,即Q∞=35MPa,b=2。

随动强化模型表征了钢材屈服面的流动,为了获得较为准确的背应力曲线,可以选取多组背应力来模拟不同应变范围下的曲线形状,第k个背应力可表示为:

(8)

式中:αk为第k个背应力张量;α为总的背应力张量;dεp为塑性应变张量增量;dεeq为等效塑性应变增量;Ck与γk为第k个背应力曲线形状参数,可通过单轴拉伸材性试验数据确定。

采用基于应力三轴度的钢材微观损伤模型,式(8)中的损伤起始准则参数a1和a2可通过单轴拉伸材性试验数据确定,试件破坏时截面减少率AR=56.27%;K、n为钢材的硬化参数,可通过钢材单轴拉伸试验获得的真实应力-应变曲线拟合得到,K=748.7MPa,n=0.19,损伤起始准则参数a1和a2如表1所示。钢材的损伤演化路径按式(6)采用,当损伤起始因子ωD达到1时单元开始发生损伤,当损伤因子D达到1时单元承载能力降为零,单元会被删除。

表1 钢材模型参数

4.2 单向加载试件M-1与数值模拟结果的对比

有限元模拟分别采用不包含和包含损伤起始与演化准则的模型,试件M-1荷载-位移曲线如图8所示。由图8可以看出,当荷载达到峰值后承载力出现退化,而不包含损伤准则的荷载-位移曲线在试验后期没有表现出承载力退化现象,包含损伤准则的荷载-位移曲线与试验结果比较吻合,表明了基于应力三轴度的钢材微观损伤模型能够较好地模拟软钢阻尼器承载力损伤退化现象。

图8 试件M-1荷载-位移曲线

试件M-1各区域的损伤演化曲线见图9,图中各区域的定义见图9。对于单调加载试件,损伤集中在颈部区域,试件其他区域基本无损伤。在加载初期,阻尼器无损伤,当位移达到35mm左右,损伤开始发展并迅速增加,直至试件颈部发生过大的塑性变形而断裂,如图10所示。

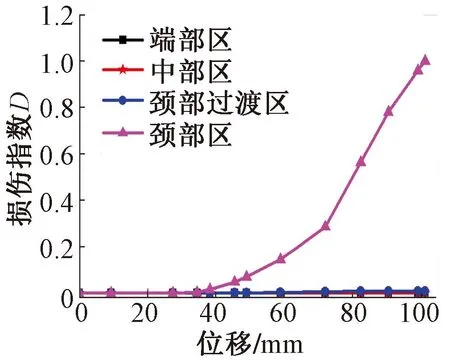
图9 试件M-1各区域损伤演化曲线

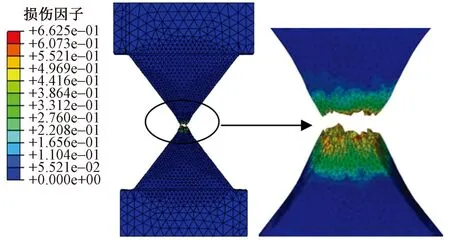
图10 试件M-1最终破坏图

4.3 循环加载试件与数值模拟结果的对比

试验得到的滞回曲线与有限元模拟结果的对比见图7。可以看出试件在循环加载下,后期表现出承载力退化现象。有限元分析结果表明,包含损伤准则的模型较不包含损伤准则的模型得到的结果更吻合,包含损伤准则的模型能够考虑大位移幅值下试件承载力的退化,说明基于应力三轴度的钢材微观损伤模型能够应用于软钢阻尼器的循环加载分析中。

试件V-1破坏时的损伤分布见图11,图中红色区域为试件发生了起始损伤,即ωD≥1,蓝色区域表示未开始损伤,即ωD<1,循环加载破坏时,试件大部分区域进入损伤状态。

图11 试件V-1破坏时损伤分布图

试件各区域的损伤演化关系见图12。由图可见:1)小位移幅值(≤30mm)作用下,阻尼器各个部位的损伤均较小,但随着循环圈数的增加,颈部过渡区和颈部区损伤逐渐增加,表现为试件V-4与试件V-3在第二级幅值作用下(30mm),颈部及颈部过渡区的损伤较试件V-2与V-1发展快;2)随着位移幅值的增加,损伤加速发展;3)试件颈部区域损伤发展最快,端部及颈部过渡区损伤发展次之,中部区域损伤发展最慢;4)最终阻尼器均是由于颈部区域损伤值D达到1而发生断裂破坏。