江苏宿迁220kV变电站隔震设计方法研究

王志浩, 赖振锋, 林康立, 杨鹏程

(1 国网江苏电力设计咨询有限公司徐州勘测设计分公司，徐州 221005；2 广州大学工程抗震减震与结构安全教育部重点实验室，广州 510405；3 苏州海德新材料科技股份有限公司，苏州 215500)

0 引言

电力系统又被称为生命线系统,是促进国民经济和社会发展的重要助力,一旦遭到破坏,会严重影响社会秩序和人民生活。在唐山、汶川及国外等地震中[1-3],变电站都会受到严重破坏,造成二次灾害。根据变电站特点,传统的抗震模式是增加建筑结构截面、加强设备连接点、降低设备重心以及采用新型高强度材料(高强珪瓷等)等。在变电站抗震研究方面,Knight B T等[4]提出一种加强变电站结构薄弱处的设计方法来改善结构抗震性能。朱爱珠、王磊等[5-6]通对比分析构架柱焊接与螺栓连接地震时程反应,建议采用高强度螺栓进行构件连接加强结构抗震能力。李天、李杰等[7]则建议采用轻型楼板,并考虑设备与楼板连接的相互作用来减小地震作用。然而上述都属于硬抗式抗震,在宿迁等高烈度地区经济性和抗震效果都有待提高[8]。

此外,变电站一般为空间较大的框排架结构,抗侧刚度较小,且内部配有荷载较大的GIS、吊车等设备。大型设备在地震时容易放大地震作用,导致结构更大的破坏。目前国内外的电力设施规范仅从设备动力放大系数和提高抗震设防做要求[9-10],在宿迁等高烈度地区,无法保证结构安全,从而会导致设备破坏。因此,众多学者对变电站的隔震设计进行研究,文波等[11-12]对变电站的隔震设计进行系统研究,结果表明隔震技术可以有效减小地震反应,使电力设备避开结构的卓越周期。张小民等[13]对西安一变电站进行隔震设计后,对现场进行测试发现,结构隔震效果良好。韩军科等[14]通过对比分析隔震与非隔震设备地震时程反应发现,设备基底隔震可以有效延长自振周期,减小地震响应。郜时昆等[15]通过隔震与传统的抗震加固措施对比,进一步说明了隔震技术在变电站中应用的优势。

然而,目前隔震采用的分部设计方法存在建模繁琐、减震系数对地震波依赖性较大以及上部结构内力与实际地震作用不符等问题。本文结合《建筑隔震设计标准》(GB/T 51408—2021)(简称隔标),提出变电站隔震一体化设计方法,随后以宿迁某220kV变电站结构为研究对象,采用传统的分部设计和一体化设计方法进行隔震设计,并对两种设计方法的支座选择、地震波选取和楼层响应分布规律等方面进行对比研究。

1 基于复模态理论的一体化设计方法

隔标中提出的一体化设计方法是基于复模态理论的反应谱设计方法,可以考虑隔震结构的非比例阻尼特性,相对于之前的强制解耦[16]精度更高。一体化设计方法的隔震层的支座参数是通过迭代过程得到,迭代直到隔震层位移不变,取此时收敛的等效参数作为隔震层的支座参数[17],其迭代原理如图1所示,其中Fi为迭代第i次的最大剪力,Di为迭代第i次的隔震层最大位移,keq,i为迭代第i次隔震层对应的等效刚度。

由于隔震层与上结构材料不同,两者的阻尼有明显差异,所以等效线性化后,其运动方程在振型空间展开具有耦合项[18]。因此,将其运动方程转换为状态空间矩阵利用复模态原理进行解耦,其运动方程为f(t):

(1)

式中:M为质量矩阵;C为等效阻尼矩阵;K为等效刚度矩阵;x为位移向量。

首先利用Foss变换[19]将式(1)转化为一阶微分方程,即:

(2)

利用复振型叠加方法,位移向量x可展开为:

(3)

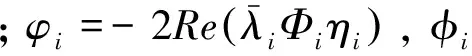
2 一体化设计方法的实施流程

目前国内隔震设计大多采用《建筑抗震设计规范》(GB 50010—2010)(简称抗规)中提出的分部设计法,该方法的核心是求得时程分析下隔震与非隔震楼层剪力或弯矩比值,选取最大比值作为减震系数β,然而减震系数β是基于所选地震波时程分析而确定,而减震效果由选取的地震波类型决定,显然是不满足安全性要求的。并且上部结构、隔震层、基础与下部结构分别设计、验算,上部结构地震作用计算和实际隔震结构存在误差。此外,分部设计法分别基于设防地震和罕遇地震下相应剪切变形所对应的参数假定支座的等效刚度和等效阻尼比,因此实际情况下支座位移往往与假定存在误差,导致等效刚度取值偏大或偏小,从而影响减震系数的大小,相应的地震作用变形验算将偏于不安全。

采用隔标中提出的一体化设计方法,其支座参数是根据实际输入地震波或反应谱得到的结果迭代而来,更加接近地震作用下的真实值,并且其核心计算理论复模态分解反应谱方法可以很好地对隔震这类非比例阻尼体系进行解耦,使得设计结果更加精准。隔标中将原来的“多遇地震不坏、设防地震可修、罕遇地震不倒”的三水准设计提升到“设防地震不坏、罕遇地震可修、极罕遇地震不倒”,大幅提高了结构的抗震性能。此外,为保证在增加安全性的前提下,提高经济性,隔标规定了对隔震结构的重要构件进行性能化设计。一体化设计方法设计流程如图2所示,其中需要注意的是地震波的选取是以隔震层等效阻尼比修正后的反应谱作为目标谱的。

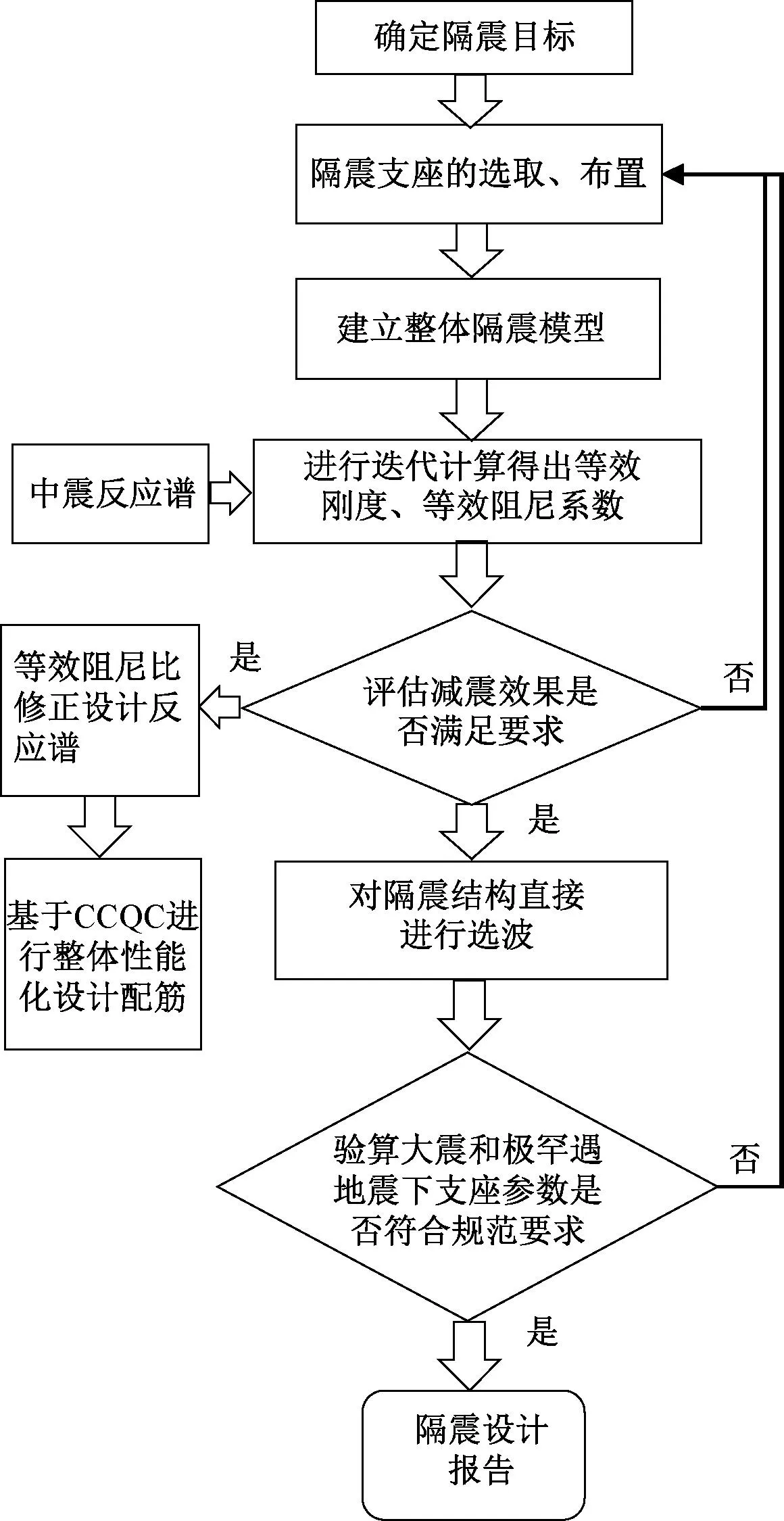
图2 一体化设计方法流程示意图

3 工程实例

3.1 工程概况

本工程为江苏宿迁某220kV变电站钢框架结构,无地下室,地上三层,一层层高5.7m,二层层高9.8m,三层层高4.0m,建筑结构高度19.5m,室内外高差0.39m,宽12.5m,高宽比1.56,结构设计合理,使用年限为50年,抗震设防烈度8度,设计基本加速度峰值为0.3g;设计地震分组第二组,Ⅲ类场地,无液化,场地特征周期0.40s;50年一遇基本风压为0.35kN/m2,地面粗糙度类别为C类。其模型如图3所示。

图3 结构有限元模型

隔震支座设置在基础和首层之间,上部结构采用框架形式,为便于两种隔震设计方法的对比分析,采用相同的隔震支座布置方案,如图4所示。但具体支座参数的确定有所不同,其中一体化设计方法采用PKPM-GZ软件进行设计,分部设计方法用PKPM和ETABS软件进行设计。

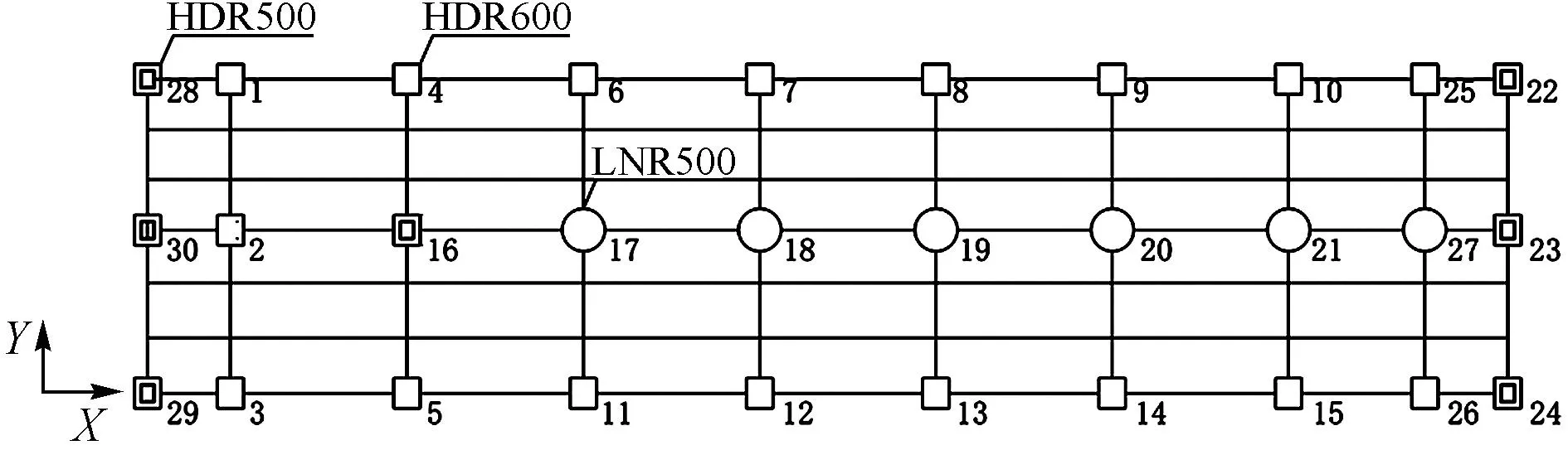
图4 支座平面布置图

3.2 支座选取

此变电站结构为典型的框排架结构,本身抗侧刚度小,并且与普通的民用建筑相比,需要考虑建筑房屋内部设备、仪器的抗震,当建筑物内部有较重要的设备、仪器时,传统抗震设计方法是不适用的[8]。此外,由于楼层上部配有荷载较大的电气设备等,结构的质量分布不均匀,支座布置也非对称,会导致一定的偏心扭转效应。因此,隔震支座的选取就至关重要。高阻尼橡胶隔震支座无需组合铅芯便可达到竖向承载力、水平恢复力和阻尼耗能一体化的效果,是一种新型环保高效隔震支座。并且支座的高阻尼特性能够显著增加结构耗能,更加适用于变电站结构。因此,本文采用高阻尼橡胶支座和天然橡胶支座,其具体布置如图4所示。

本文采用两种隔震设计方法,分部设计方法初选支座参数如表1所示,由供应厂商提供,表1中100%和250%的含义为支座在设防地震和罕遇地震下分别取100%剪切变形和250%剪切变形,但实际情况下支座位移往往有误差,这会导致相应的减震系数偏大或者偏小。一体化设计方法通过迭代过程确定支座参数,其中天然橡胶支座假设为理想线性模型,不提供附加阻尼,高阻尼橡胶支座采用双折线模型,其迭代结果如表2所示,表2中支座位移取值为HDR500和HDR600支座每次迭代的最大位移。从表2中可以看出在设防地震作用下,结构等效阻尼比为14.52%,支座参数为实际地震作用下的取值,而不是简单地取100%和250%剪切变形对应的等效参数。

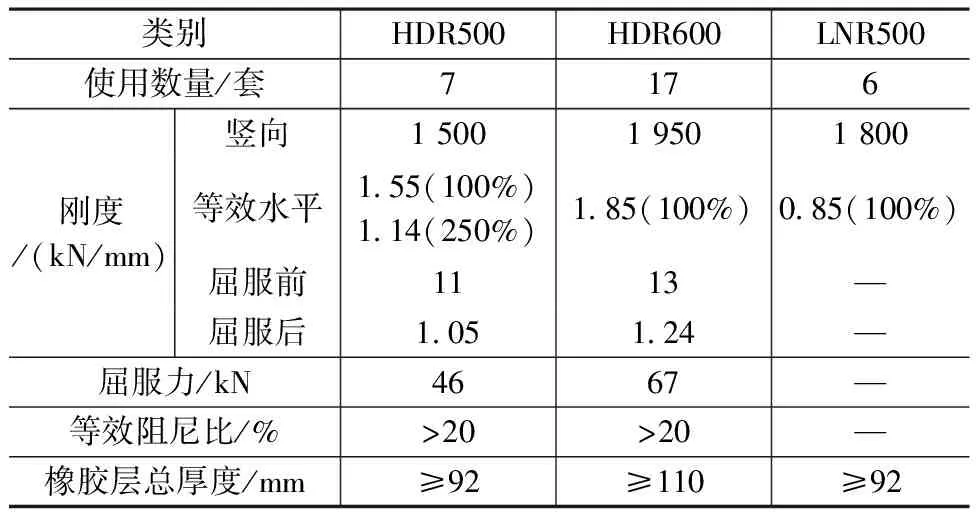
表1 分部设计支座参数

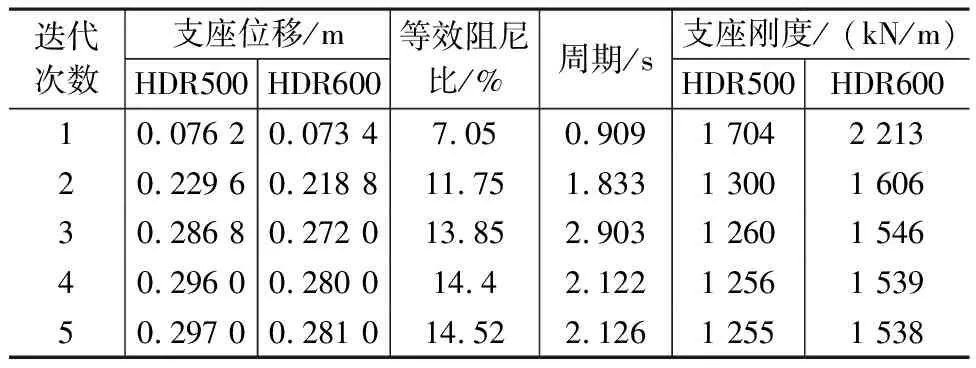
表2 一体化设计支座参数

3.3 地震作用输入

图5为不同等效阻尼比规范反应谱与相应人工波反应谱,图中图例为等效阻尼比数值,实线为不同等效阻尼比下的规范反应谱,虚线为不同等效阻尼比下的人工波反应谱。从图中可以看出,随着结构等效阻尼比的的增大,人工波反应谱的加速度降低速率是明显大于规范反应谱的,因此如果采用5%等效阻尼比生成的人工波作用于大阻尼的隔震结构会导致地震响应结果偏小,传统分部设计法则是在这种情况下通过选波进行时程分析得到减震系数β,进而对上部结构进行设计,因此可能造成结构设计的不准确以及支座验算的不合理。

图5 不同等效阻尼比规范反应谱与相应人工波反应谱

隔标中建议采用实际迭代得到阻尼比修正的反应谱为目标谱进行隔震结构一体化设计,通过迭代得到的目标谱进行人工波生成和地震波的选择来验算支座在罕遇和极罕遇地震下的性能状态。并且直接对隔震结构选波,不需要兼容非隔震结构,减轻了选波难度。图6为分部设计和一体化设计选取的地震波反应谱与目标反应谱曲线。可见,一体化设计采用的目标反应谱为“三段式”反应谱,更加契合长周期结构,并且可以看出两种设计方法选出的地震波差异较大。

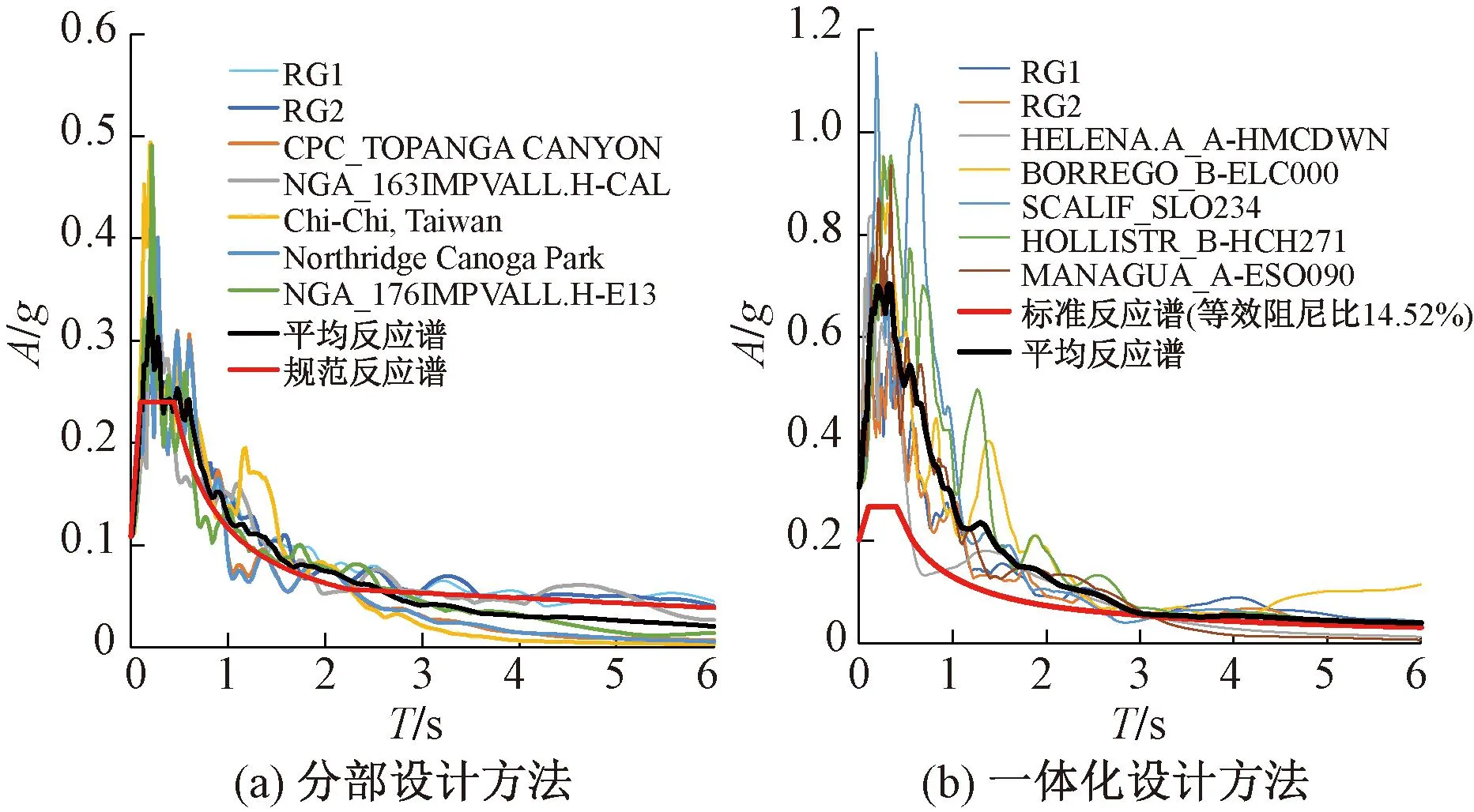
图6 不同隔震设计方法地震波反应谱与目标反应谱

3.4 隔震评估

分部设计方法是通过对隔震结构与非隔震结构进行时程分析求得减震系数 ,然后利用减震系数对上部子结构进行降度设计,也是通过减震系数判断隔震效果。由于结构基底剪力与构件内力大小息息相关,而隔标中推荐采用隔震结构一体化设计,因此隔标第6.1.3条规定隔震结构底部剪力比不大于0.5时,上部结构可按本地区设防烈度降低1度确定抗震措施。

图7为不同隔震设计方法减震效果评估对比。从图7中可知,除隔震层(1层)外,最大减震系数为0.303,达到了抗规要求,可以降度设计;一体化设计方法底部最大剪力比为0.44,同样达到了隔标的降度设计要求。其中分部设计方法是将上部结构与隔震层分开进行降度小震设计,一体化设计方法是对隔震结构整体以修正的三段式目标反应谱为输入进行中震设计。

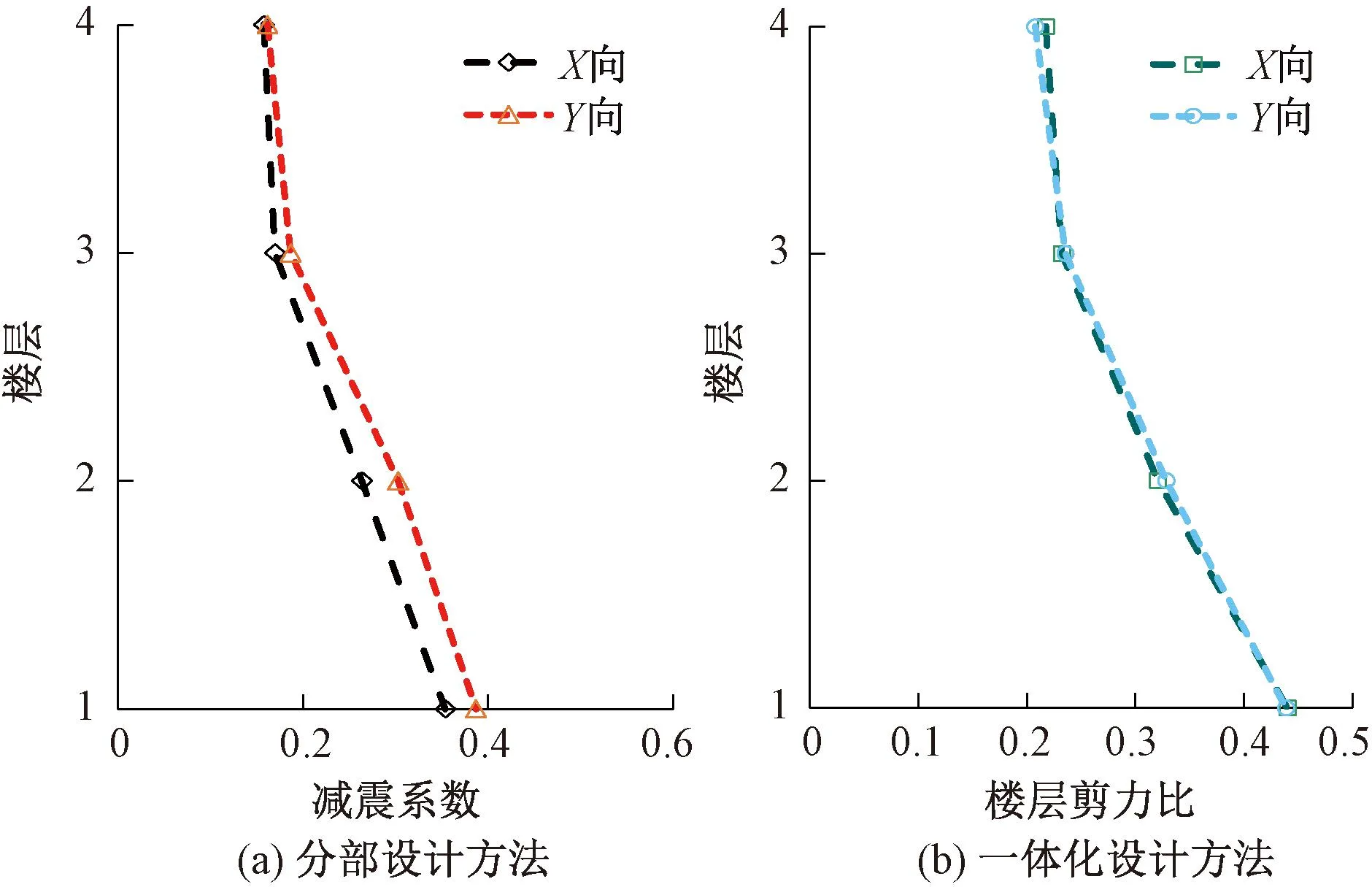
图7 不同隔震设计方法减震效果评估

为进一步对两种设计方法的隔震效率进行评估,以楼层剪力大小定义隔震率S:

(4)

式中Qf和Qg分别为非隔震和隔震结构的楼层剪力。

分部设计方法的隔震率通过七条地震波作用下楼层剪力平均值进行计算,隔震率在60%～80%之间。一体化设计方法的隔震率通过如图8所示的反应谱作为输入的楼层剪力进行计算,隔震率在55%～80%之间。由此可知两种设计方法都有较好的隔震效果,隔震率相当。然而,分部设计方法减震系数的计算依赖于地震波的选取,而地震波随机性较大,对确保结构的安全性不易把握。此外,分部设计方法不能准确反映隔震结构的受力特性,因此隔震结构设计更推荐一体化设计方法。

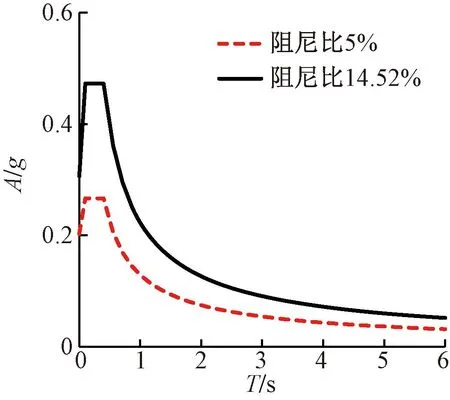
图8 不同阻尼比设计反应谱

由于变电站内部仪器对楼层加速度响应比较敏感,因此楼层加速度的降幅对评估变电站的安全有重要参考价值。对隔震结构顶层加速度降低效果进行分析。图9和图10分别为在设防和罕遇地震状态下采用抗震设计、一体化设计和分部设计方法时,同一条地震波作用下结构顶层加速度时程曲线图。由图9和图10可知,分部和一体化设计方法无论在设防地震还是罕遇地震作用下,都可以很好地降低结构楼层加速度,尤其在罕遇地震作用下隔震效果尤为明显,并且一体化设计方法的降低幅度大于分部设计方法,一体化设计方法的支座参数通过迭代而来,最接近真实的楼层加速度响应,因此采用一体化设计方法可以更好地降低加速度对内部仪器的影响。

图9 设防地震作用下结构顶层加速度时程曲线

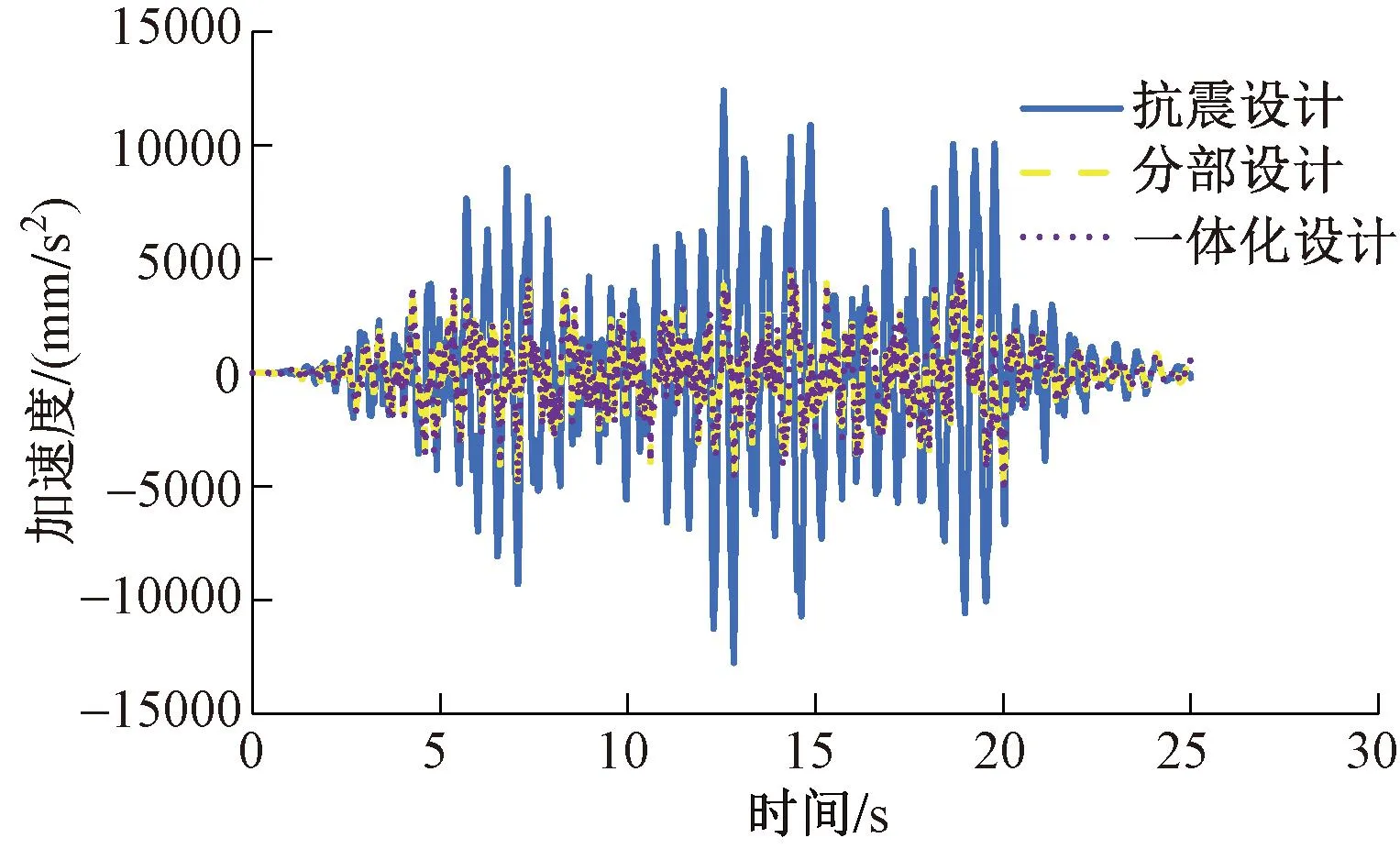
图10 罕遇地震作用下结构顶层加速度时程曲线

图11为不同设计方法X、Y向楼层内力响应,其中楼层层间位移角不包含隔震层。从图中可以看出一体化设计方法底部地震作用下相比分部设计降度增大将近2.5倍,上部增大1.5倍,并楼层剪力和弯矩响应介于降一度和不降度之间,说明可以实现隔标中震弹性目标要求的同时将构件进行优化,从而提高经济性。

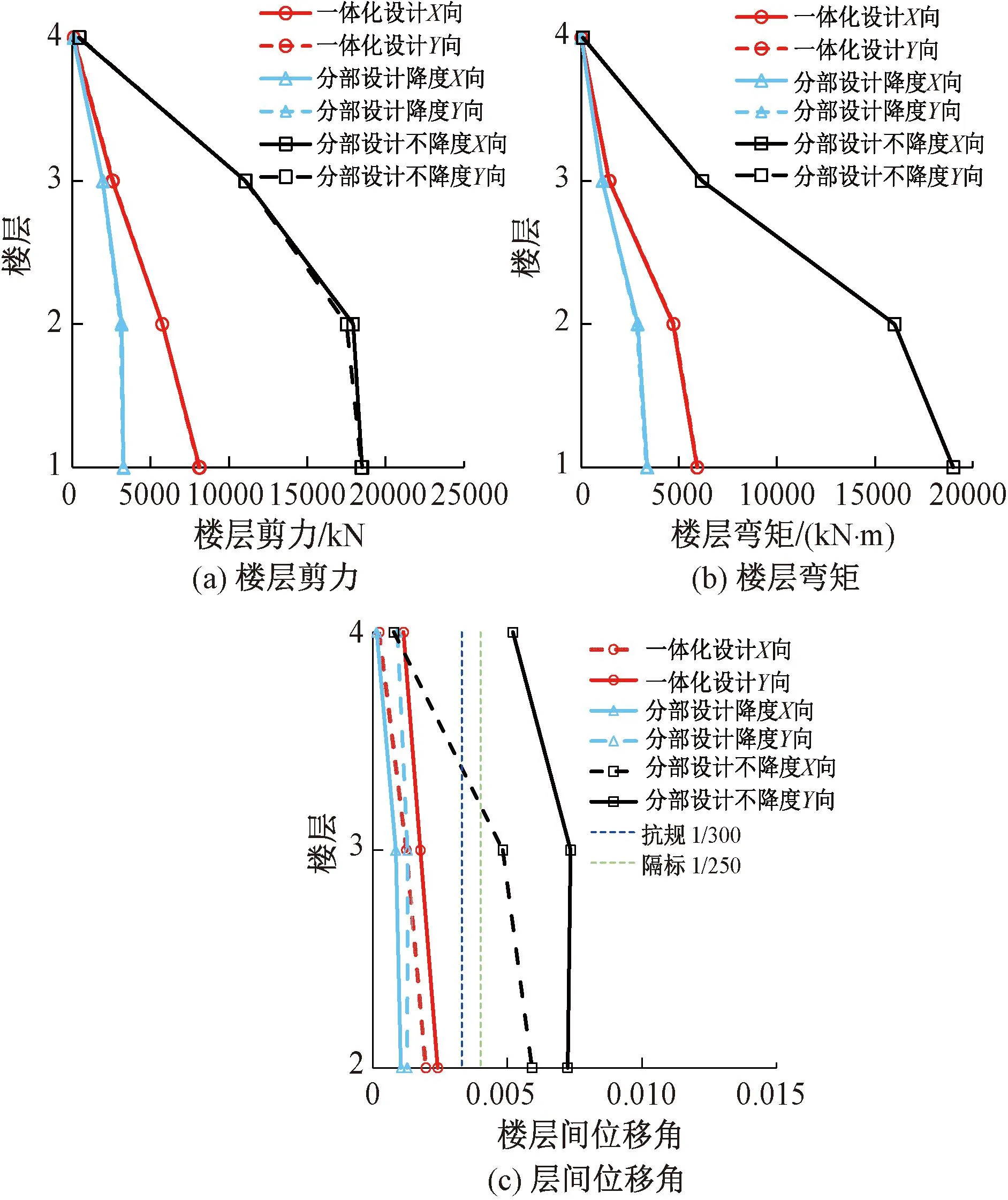
图11 不同设计方法楼层响应图

从楼层层间位移角来看,不利方向为Y向,一体化设计方法最大层间位移角为1/415,在隔标规定的1/250的限值内,满足弹性要求;分部设计方法在降度设计情况下最大层间位移角为1/775,满足抗规1/300限值要求,并且远远小于限值,进行上部优化设计时,可能会误导设计人员,造成结构不安全;由于基于反应谱的一体化设计方法考虑了比较接近实际情况的隔震层参数,从楼层位移可知,一体化设计方法底部楼层位移比分部设计方法大得多,所得的隔震层位移与分部设计方法相比会偏于安全。

4 隔震层参数影响

为研究隔震层参数对结构隔震设计方法的影响,将结构简化为层剪切模型,简化后结构参数信息见表3。

表3 隔震结构模型参数

以时程分析结果为基准,取隔震层等效周期为3s,按照分部设计(CQC)、一体化设计 (CCQC)和时程分析方法分别计算结构响应,然后以时程分析结果为基准得到CQC和CCQC的相对误差随隔震层等效阻尼比变化的趋势,见图12。同样取隔震层阻尼比为0.15,以时程分析结果为基准,得到CQC和CCQC的相对误差随隔震层等效周期变化的趋势,见图13。其中,为避免天然波离散型较大,采用以图8所示的阻尼比为14.52%的反应谱为目标谱生成人工波,本文时程分析结果为10条人工波的均值。

图12 CCQC和CQC不同楼层响应对比图

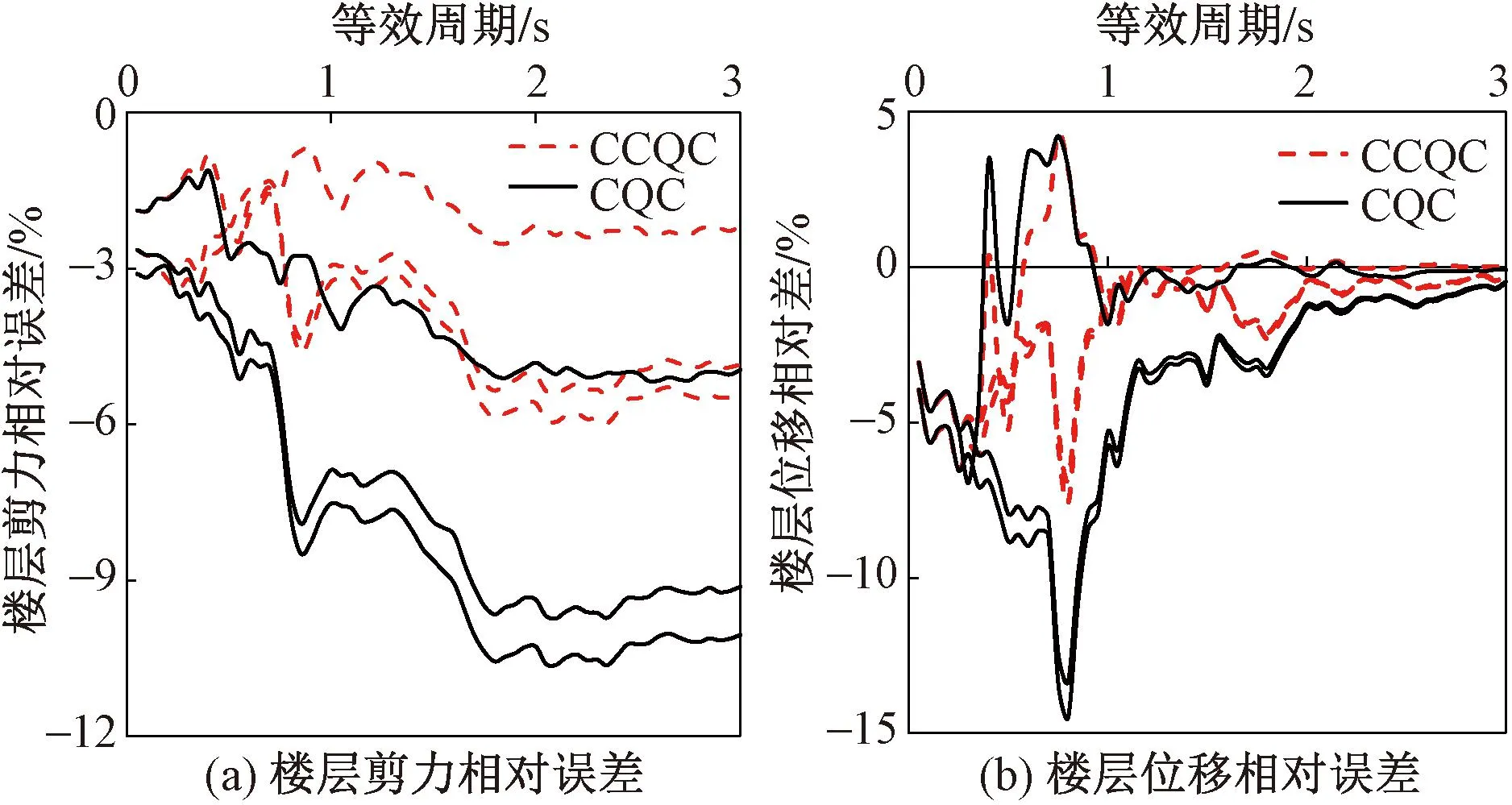
图13 CCQC和CQC不楼层响应对比图

图12中曲线表示隔震层上部楼层的剪力和位移相对误差。由图12可知,隔震层等效阻尼比在0.1以内时,分部设计方法与一体化设计方法两者相对时程分析的楼层剪力相对误差相当,此时两种设计方法都可以采用。当隔震层等效阻尼比在0.1～0.3之间时,CQC楼层剪力相对误差在10%～30%之间,并且偏小,这在工程上是不能接受的。CCQC楼层剪力相对误差始终保持在5%左右。同样可知,隔震层等效阻尼比在0.1以内时,CQC和CCQC的楼层位移相对误差相当,但是等效阻尼比在0.1～0.3时,CQC楼层位移相对误差在1%～8%之间,并且偏小,而CCQC楼层位移相对误差则保持在1%左右。由于隔震结构等效阻尼比大部分在0.1～0.3之间,因此建议采用一体化设计方法进行结构隔震分析。本文隔震结构等效阻尼比为0.145,进一步说明本文结构适用一体化设计方法。

图13中曲线表示隔震层上部楼层的剪力和位移相对误差。由图13可知,在1～3s的等效周期范围内,CCQC的楼层剪力和位移相对误差都在5%左右,而CQC楼层剪力和位移相对误差最大值可达12%,其中位移相对误差随着周期的增大有所减小。总之可以看出隔震结构按照一体化方法进行分析相对误差较小,较为合理。

5 非比例阻尼影响

一般非比例结构阻尼矩阵C不是对角阵,不能对角化,其包含模态耦合系数,即:

(5)

隔震结构为一典型的非比例阻尼体系,目前没有适宜的指标参数对其非例阻尼特性影响进行衡量,因此引入非比例特征指标[21]对隔震结构的非比例阻尼特性影响进行判定。

将矩阵D设为矩阵C的对角元素组成的对角矩阵,即D=diag(c11,c22,…,cnn)。将矩阵D-1C的最小特征值和最大特征值分别表示为Smin和Smax,定义非比例特征指标I(C)[21]为:

I(C)=(Smax-Smin)/(Smax+Smin)

(6)

I(C)是单调递增函数,其取值范围为 0 ～ 1,当I(C)=0 时,表示结构为比例阻尼结构;I(C)值越大,越远离比例阻尼特性,阻尼非比例性越强。本文变电站隔震结构非比例特征指标为0.5,说明具有非比例阻尼特性,且影响较大。

为了进一步得到非比例阻尼特性对隔震设计的影响规律以及与非比例阻尼指标的关系,将基于等效线性化强制解耦的反应谱CQC法和基于等效线性化正常解耦的反应谱CCQC法的分析结果相对误差进行对比分析。

图14为两种方法在同一输入反应谱下,与时程分析结果的楼层响应相对误差,其楼层响应相对误差定义为:

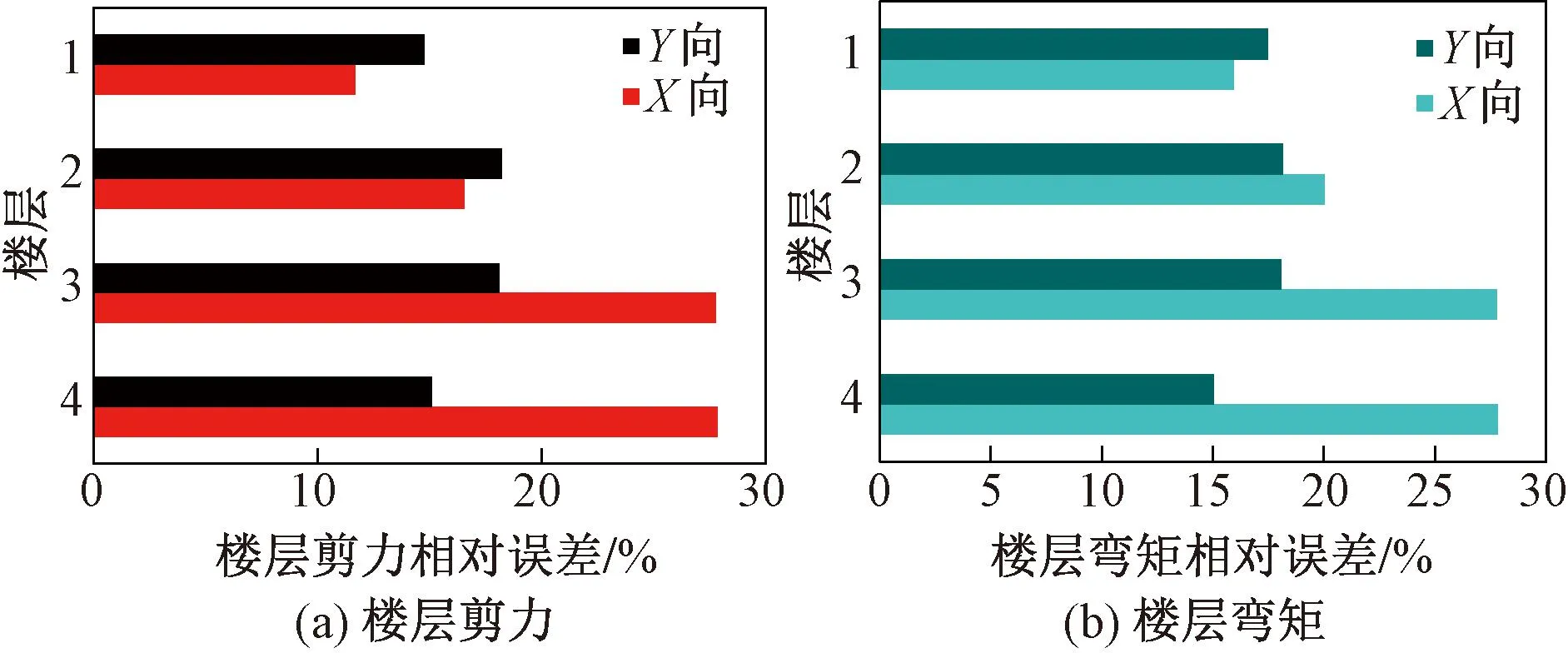
图14 两种方法相对误差

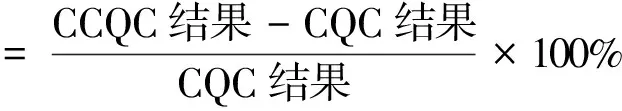
从图14中可以发现,相对误差都为正值,最大在X向,且在顶层,其中楼层剪力相对误差在11%～28%,楼层弯矩相对误差在15%～28%,可以看出忽略非比例阻尼影响会导致楼层响应结果偏小,对较高楼层影响显著,且相对误差较大不能满足实际工程的需求,建议在进行结构隔震设计时考虑非比例阻尼的影响,采用隔标提出的一体化设计方法。

6 结论

(1)变电站隔震结构非比例阻尼指标为0.5,非比例阻尼特性较强,且对其楼层响应结果影响较大,相对不考虑非比例阻尼特性影响的分析方法,相对误差最高可达27.87%,实际隔震设计中不可忽略非比例阻尼影响。

(2)隔震结构等效阻尼比在0.1～0.3之间时,采用分部设计方法的强制解耦非线性时程分析误差在10%～30%之间,而随着隔震结构周期增大楼层剪力和位移相对误差都有先增大后减小趋势,相对误差可达12%左右。一体化设计方法的复模态分析方法所得楼层剪力和位移在隔震层参数发生变化时精确度比较稳定,相对误差始终保持在5%左右。

(3)一体化设计方法下的变电站楼层响应是分部设计方法的1.5～2.5倍之间,楼层响应介于分部设计方法降一度和不降度设计之间,可以实现中震弹性目标要求的同时将构件进行优化,提高结构经济性。

(4)隔震结构实际的人工波反应谱的加速度降低速率明显大于规范反应谱,采用5%阻尼比生成的人工波作用于隔震结构,会导致地震响应结果偏小,以迭代得到的隔震层阻尼比作为结构阻尼比选取地震波更合理。

(5)支座参数不能简单地取100%和250%剪切变形对应的等效参数,应采用实际地震作用下迭代得到的支座参数,更加符合隔震结构在实际地震作用下的受力情况。